Cite this Article
Wang Jia, Sheng Ai-Guo, Huang Xin, Li Rong-Yu, He Guang-Qiang. Eigenvalue spectrum analysis for temporal signals of Kerr optical frequency combs based on nonlinear Fourier transform. Chinese Physics B, 2020, 29(3): 034207  
Permissions
Eigenvalue spectrum analysis for temporal signals of Kerr optical frequency combs based on nonlinear Fourier transform
Wang Jia1, Sheng Ai-Guo1, Huang Xin1, Li Rong-Yu1, He Guang-Qiang1, 2, 3, †
State Key Laboratory of Advanced Optical Communication Systems and Networks, Department of Electronic Engineering, Shanghai Jiao Tong University, Shanghai 200240, China
State Key Laboratory of Precision Spectroscopy, East China Normal University, Shanghai 200062, China
National Laboratory of Solid State Microstructures, Nanjing University, Nanjing 210093, China

 

† Corresponding author. E-mail: gqhe@sjtu.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 61475099 and 61922040), Program of State Key Laboratory of Quantum Optics and Quantum Optics Devices, China (Grant No. KF201701), and the Key R&D Program of Guangdong Province, China (Grant No. 2018B030325002).

Abstract

Based on the nonlinear Schrödinger equation (NLSE) with damping, detuning, and driving terms describing the evolution of signals in a Kerr microresonator, we apply periodic nonlinear Fourier transform (NFT) to the study of signals during the generation of the Kerr optical frequency combs (OFCs). We find that the signals in different states, including the Turing pattern, the chaos, the single soliton state, and the multi-solitons state, can be distinguished according to different distributions of the eigenvalue spectrum. Specially, the eigenvalue spectrum of the single soliton pulse is composed of a pair of conjugate symmetric discrete eigenvalues and the quasi-continuous eigenvalue spectrum with eye-like structure. Moreover, we have successfully demonstrated that the number of discrete eigenvalue pairs in the eigenvalue spectrum corresponds to the number of solitons formed in a round-trip time inside the Kerr microresonator. This work shows that some characteristics of the time-domain signal can be well reflected in the nonlinear domain.

PACS: ;42.65.Sf;;42.65.Tg;
Keyword:;nonlinear Fourier transform;;Kerr optical frequency combs;;nonlinear signal processing;
1. Introduction

The nonlinear Fourier transform (NFT), also known as the inverse scattering transform (IST), is a powerful mathematical tool to solve the problems of wave propagation in some certain nonlinear media, especially in the field of soliton theory.[1] In contrast with the linear Fourier transform (FT), where the signal is decomposed into the superposition of sine waves so as to obtain the frequency components in the linear frequency domain, the nonlinear Fourier transform can decompose the signal into soliton components and non-soliton components (also known as radiation components) to obtain the corresponding nonlinear frequency components.

In recent years, NFT has been widely used in the field of optical fiber communication. The nonlinear Schrödinger equation (NLSE) is the mathematical model to describe the signal propagation in the optical fiber channel.[2–4] Without considering the channel noise, NLSE can be approximated as an integrable partial differential equation. In this case, the complex evolution problems of time-domain signal and linear spectrum can be converted into a simple nonlinear spectrum evolution problem by using NFT.[5–7] Based on this characteristic, many researchers have carried out a series of theoretical studies and experiments to reduce the unfavorable restriction brought by fiber nonlinearity to optical fiber communication.[8–12] The realization of high-speed and reliable fiber communication system has proved the superiority of NFT in solving the NLSE problem.[13–15] In 2018, Ryczkowski et al.[16] used NFT to analyze the transient dissipative soliton dynamics in a mode-locked laser, clearly observed the presence of local soliton content, and promoted the application of NFT in describing ultra-short pulses.

In this paper, we use NFT to study the temporal signals of Kerr optical frequency combs (OFCs) based on Kerr microresonator. The Kerr OFCs are presented as a series of precisely equidistant spectral lines with extremely narrow linewidth in the linear frequency domain, and the corresponding time-domain signals of OFCs in stable soliton state are presented as periodic ultra-short laser pulse sequences.[17,18] We can clearly distinguish the unstable state and different stable states of OFCs, including the chaos, the Turing patterns, and various soliton states, according to the eigenvalue spectrum obtained by NFT for various temporal signals in the cavity. We also find that the number of discrete eigenvalue pairs is consistent with the number of solitons formed in the intracavity round-trip time.

2. The theory
2.1. The model for Kerr OFCs generation

The generation of Kerr OFCs is described by the spatiotemporal Lugiato–Lefever equation (LLE) whose normalized form follows[19,20]

On the left-hand side, Ψ(τ,ϕ) is the complex envelope of the intracavity field, and τ denotes the normalized time. On the right-hand side, ζ0 = 2(ω0 − ωp)/κ denotes the normalized detuning of the pump laser ωp from the resonance frequency ω0, κ stands for a coupled resonance width (also known as the total linewidth), ϕ is the co-rotating angular coordinate inside the resonator, and β = −2D2/κ is the overall dispersion parameter with D2 being the second-order dispersion, that is, the anomalous group velocity dispersion (GVD) regime follows β < 0, while the normal GVD regime is defined by β > 0. f represents the dimensionless external pump field intensity, for completeness, f can be calculated by

Here, Pin is the optical power (in W) of the laser pump at the input of the resonator, is the nonlinear coupling coefficient, ħ is the reduced Planck constant, c is the speed of light in vacuum, n0 and n2 are the linear and nonlinear refraction indices of the material, respectively, and Veff denotes the effective volume of the pumped mode. η = κext/κ is the coupling efficiency related to coupling (or extrinsic) linewidth κext and total linewidth κ, where κ = κin + κext and κin is the intrinsic linewidth.

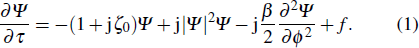
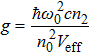
We then consider the dimensionless longitudinal coordinate θ = ϕG in the anomalous GVD regime (β < 0), where and d2 = D2/κ is the dimensionless dispersion. Equation (1) can be further simplified to[21,22]

which is known as the nonlinear Schrödinger equation with damping, detuning, and driving. When the interaction between dispersion and nonlinearity effect is counteracted and the energy in the cavity is balanced, dissipative solitons with invariant envelope along the propagation will be formed in the time domain, and in turn stable OFCs will be generated in the linear frequency domain. In other words, the soliton solution can be the stable solution to Eq. (3), which is similar to the standard normalized NLSE. Based on the similarity between them, in this paper, we use NFT for NLSE to analyze the intracavity signal governed by Eq. (3).

2.2. Periodic nonlinear Fourier transform

There are now a lot of detailed NFT algorithms for NLSE, both for periodic boundary condition[23] and non-periodic boundary condition, and the latter is usually called vanishing boundary condition.[24] The basic idea for Eq. (1) is to treat the light propagating in the circular direction inside the resonator as the signal propagating along an unfolded track with periodic boundary conditions,[25] that is,

The above periodicity also applies to Eq. (3) by changing the value of l. Thus, the NFT algorithm with periodic boundary condition is adopted in this work. According to Ref. [23], where the fast nonlinear Fourier transform (FNFT) for the periodic boundary condition was introduced, the nonlinear frequency domain after FNFT includes two parts: the main spectrum and the auxiliary spectrum.[26] The auxiliary spectrum is also known as the hyperelliptic mode, which is not within the scope of this paper. Our work focuses only on studies of the main spectrum which consists of discrete eigenvalues that remain invariant during pulse evolution according to the standard NLSE (all terms on the right-hand side of Eq. (3) vanish). The eigenvalue, also known as the nonlinear frequency, is the nonlinear analogue of the frequency given in FT. The difference between the two is that the latter refers to real numbers, while the former is distributed in the complex plane and has real axial symmetry.

For the standard NLSE, its NFT is indeed the IST of Zakharov–Shabat problem (ZSP) which can be expressed in the following form:[1]

where Ψ is the complex envelope of the time-domain signal, and Ψ* denotes its conjugate signal. The nonlinear frequency parameter λ is a complex eigenvalue, i.e., λ = Re(λ) + jIm(λ), whose real part reflects the frequency and imaginary part reflects the amplitude of the corresponding time-domain signal. More detailed theory can be found in the next section. v = [v1 v2]T represents the eigenvector which subjects to the eigenvalue function Lv = λ v, and

is an operator whose eigenvalues are independent of time ϕ. For the fact that we just consider the signal in one period, the solutions of Eq. (5) are denoted as Φ(ϕ) and with the canonical initial conditions (ϕ0 corresponds to the left boundary of the signal in a period)

Define the so-called monodromy matrix

and its Floquet discriminant , where ϕl corresponds to the right boundary of the signal in a period according to Eq. (5). Then we can obtain the eigenvalues space by the following method when D euqidistant samples of the signal Ψ are given:

The eigenvalues space consists of discrete complex numbers and can be called as the eigenvalue spectrum in the nonlinear frequency domain. In this work, we only give a brief description of the basic concept of FNFT, and interested readers may refer to Ref. [23] for the detailed derivation process.

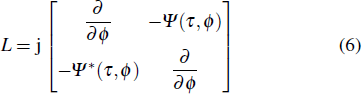
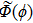
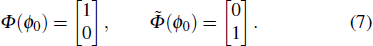
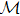
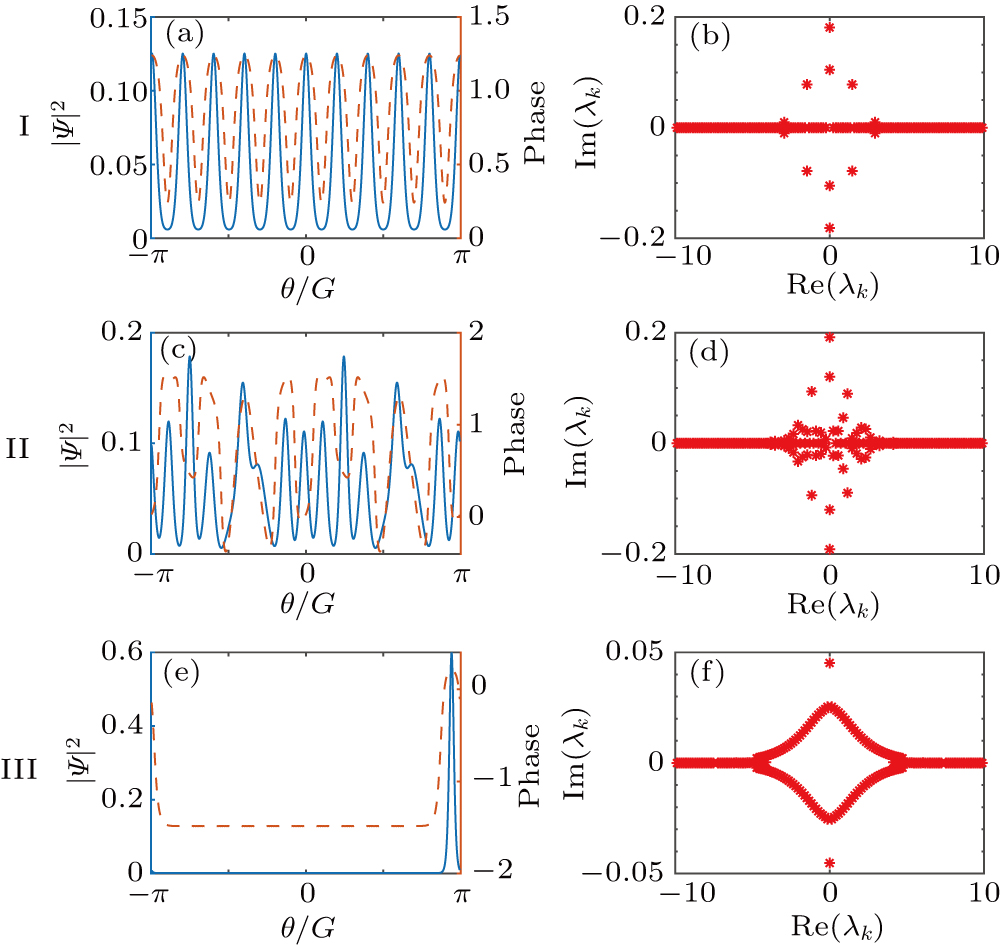
Since any signal can be regarded as the combination of soliton component and radiation component, although either of these two can be absent for some specific case,[26] the eigenvalue spectrum obtained from NFT actually consists of two parts, the eigenvalues corresponding to the soliton component and the eigenvalues corresponding to the radiation component of the signal. Figure 1 shows the eigenvalue spectra of 4 different signals via NFT.

Fig. 1. The eigenvalue spectrum distribution of (a) Ψ(t) = sech (t)ej 0.5; (b) Ψ(t) = sech (2t)ej 0.5; (c) Ψ(t) = sech (t)ej sech (t); (d) Ψ(t) = 2 sech (2t)ej 0.5. Each inset shows the intensity and phase features of the corresponding time domain signals.

According to Matsuda et al.,[27] signals in the form of u(t) = A sech (At) (A is a real number) can be a soliton solution (i.e., stationary solution) of NLSE and have definite eigenvalues ± j A/2. When the phase of such a signal is constant, the eigenvalue occurs at the same position, just as Figs. 1(a) and 1(d) show. There are obvious isolated discrete eigenvalues at ± 0.5j for signal Ψ(t) = sech (t)ej 0.5 and ± 1 j for signal Ψ(t ) = 2 sech (2t)ej 0.5, and the remaining eigenvalues are all 0. In this sense, we relate such isolated eigenvalues in the eigenvalue spectrum to the soliton component in any signal and the remaining to the radiation component. Considering the physical meaning of eigenvalue λ, a pulse in the form of u(t) = A sech (At) can also be understood as a signal containing a single nonlinear frequency. Figure 1(b) gives the eigenvalue spectrum of signal Ψ1(t) = sech (2t)ej 0.5 and all the eigenvalues as shown in the eye-like structure are related to non-soliton signal component because no obvious isolated discrete eigenvalues can be observed. Here we again recall the physical meaning of eigenvalues and it is worth to mention that when the pulse u(t) = sech (At) gets narrower by increasing A, the eye-like structure expands horizontally. That is to say, a narrower time domain signal corresponds to an increase in the nonlinear frequency component, which is a property similar to that of the linear spectrum. By taking the time-variant phase into consideration, an eye-like structure will also appear near the real axis of λ. As a result, the soliton eigenvalues become below the ideal eigenvalues of ± 0.5j in Fig. 1(c) compared with Fig. 1(a), which is subjected to the Parseval identity.[1] In short, different time domain signals show distinct nonlinear frequency domain characteristics via NFT, which is the basis of our work.

3. Eigenvalue spectrum analysis based on periodic NFT
3.1. Case 1

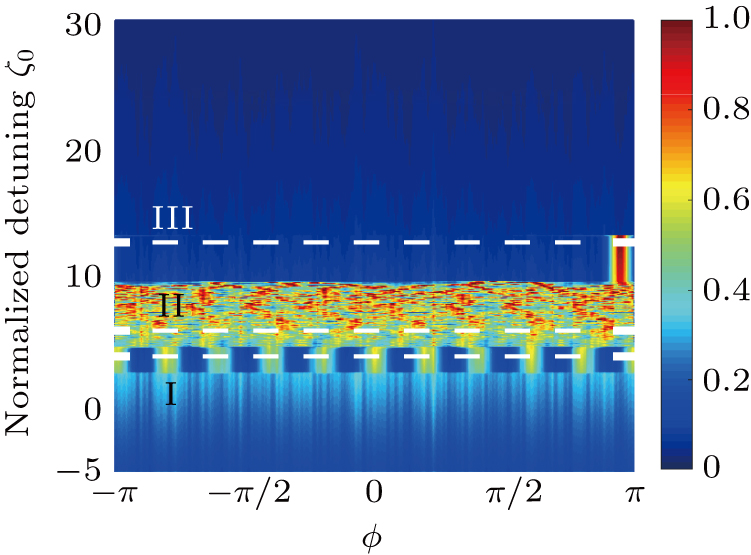Based on the above property, we can study different signals in the Kerr microresonator, and we use two different sets of parameters for the Kerr OFCs simulation. We first start with a simple case of forming an optical frequency comb with one-way scan of the pump laser. Figure 2 shows the temporal evolution, and the related simulation parameters are Pin = 0.755 W, λ0 = 1550 nm, κ/2π = 287 MHz, n0 = 2.122, n2 = 2.4 × 10−19 m2/W, D1/2π = 44.48 GHz, D2/2π = 12.5 MHz, Veff = 3.6594 × 10−15 m3, and η = 0.9989.

Fig. 2. The temporal evolution diagram inside the Kerr microresonator during one-way scan of the pump laser.

As can be seen from Fig. 2, different states can be obtained from different detuning via tuning by scanning the pump laser frequency. Clearly, there are four distinct time-domain signals corresponding to the pump laser, Turing pattern, chaos, and soliton state, respectively. It is important to point out that the so-called soliton state here corresponds to the stable solution to Eq. (5) and is different with the soliton component defined early. The periodic FNFT is then performed to these signals and we try to find their corresponding nonlinear spectrum characteristics. Due to the simplicity of the linear frequency domain when there is only pump light in the cavity, we do not consider its nonlinear domain in this paper. Figure 3 shows the time-domain signals (left column) of interest in Fig. 2 and their eigenvalue spectra (right column).

Fig. 3. The intensity and phase portrait of the intracavity signals (left column) and the corresponding eigenvalue spectra obtained by FNFT (right column). The corresponding normalized detunings are (a) ζ0 = 3.86, (c) ζ0 = 5.63, (e) ζ0 = 12.68.

Figure 3(a) describes the time-domain signal of the Turing pattern, which is a state of modulation instability. As shown in Fig. 3(b), its eigenvalue spectrum is strictly symmetric, with respect to both the real axis and the imaginary axis. The eigenvalue spectrum includes several isolated discrete eigenvalue pairs, showing several nonlinear frequency components. According to the specific distribution of the eigenvalues, the Turing pattern temporal signal includes some soliton components defined in our paper because there are eigenvalues on the imaginary axis of the eigenvalue spectrum. The time-domain signal for chaos which can arise in any nonlinear system is shown in Fig. 3(c), and its eigenvalue spectrum (Fig. 3(d)) is also disorderly. When the energy in the cavity reaches an equilibrium, and the dispersion and nonlinear effects cancel each other out, the dissipative soliton forms as shown in Fig. 3(e). Its eigenvalue spectrum includes obvious quasi-continuous eigenvalues corresponding to the radiation component and a pair of soliton discrete eigenvalues, where the imaginary part of the discrete eigenvalues can reflect the amplitude feature of the soliton. It needs to be noted that, sometimes, breathing solitons will occur in the tuning process, that is, the intensity of a temporal soliton will change periodically with time. Under this circumstance, the position variation of the discrete eigenvalues can be utilized to judge the existence of a breathing soliton. Thus, according to different distributions of eigenvalues of these signals, we can easily distinguish different stages during the forming of OFCs in the nonlinear frequency domain.

3.2. Case 2

Next, we consider the more complex case of Kerr OFCs generation with multiple temporal solitons existing in a round-trip time. The necessary simulation parameters are listed as in Ref. [22] Pin = 2 W, λ0 = 1553 nm, κ/2π = 300 MHz, n0 = 2.4, n2 = 2.4 × 10−19 m2/W, D1/2π = 100 GHz, D2/2π = 2.5 MHz, and Veff = 1.0 × 10−15 m3. Here, we apply the different parameter η = 0.50 which is the critical coupling efficiency. The resulted temporal evolution diagram is shown in Fig. 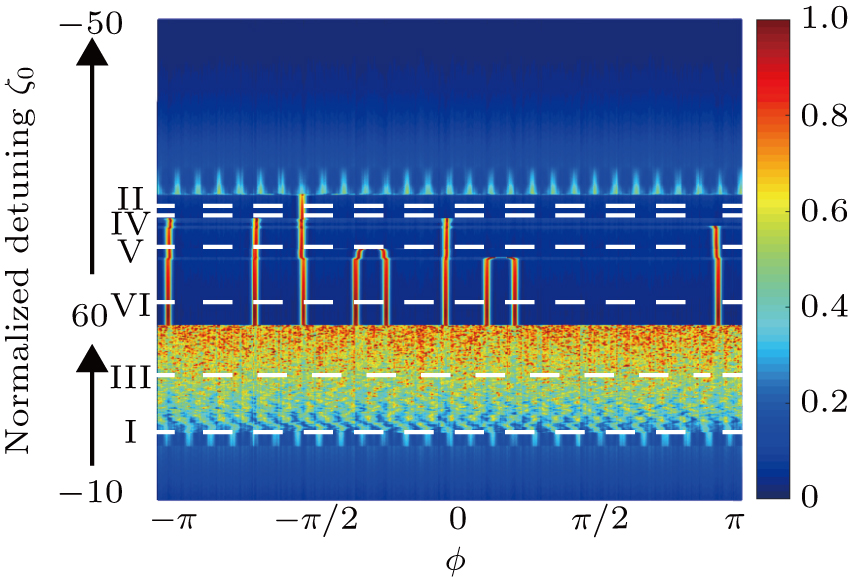4. In this simulation for the generation of Kerr OFCs, the pumped laser frequency is scanned forward and backward, that is, we gradually decrease ωp and then increase it, which can be observed from the variation of the normalized detuning in the figure. Thus, by combining the tuning process with thermal effect, abundant soliton dynamic processes can be formed in the Kerr microresonator. Similarly, the time-domain signals of interest are extracted from the tuning process, including the Turing pattern, chaos, single soliton, and multi-solitons state.

Fig. 4. The temporal evolution diagram inside the Kerr microresonator by thermal effect and forward and backward tuning of the pump laser.

First, we analyze the time-domain signals of Turing pattern and single soliton state. Figure 5 shows the temporal intensity and phase profiles, linear spectrum, and nonlinear eigenvalue spectrum of these two signals. In this case, the generated Turing pattern and soliton signal within an intracavity round-trip time are different from those in case 1, and the obtained eigenvalues are quite different. However, the distribution of eigenvalues follows the same rule, i.e., strictly symmetric discrete eigenvalue pairs for the Turing pattern (see Fig. 5(e)), and combination of a pair of discrete eigenvalues and quasi-continuous spectrum with obvious eye-like structure for the single soliton pulse (see Fig. 5(f)). Figures 5(c) and 5(d) show the linear spectrum. A few frequency components exist in the linear domain for the signal with Turing pattern, which is also known as the modes of the primary comb. Once a stable dissipative soliton pulse is formed, the optical frequency comb with smooth and stable envelope and wide band will be generated as Fig. 5(d) shows, which is also what we hope to get. Here, we discover that there is a certain correlation between the nonlinear eigenvalue spectrum and the linear spectrum for the fact that the real part of the eigenvalue represents the frequency of the signal. That is, for the signal with Turing pattern, there are only a few frequency components either in the linear or nonlinear frequency domain. For a single soliton pulse, except for a pair of isolated eigenvalues corresponding to the soliton component of the initial signal, all the other nonlinear frequency points are smoothly and uniformly distributed in the nonlinear frequency domain, which is also a property of linear frequency lines distribution.

Fig. 5. The temporal intensity and phase profiles, linear spectrum, and nonlinear eigenvalue spectrum of Turing pattern (left column) and single soliton state (right column). ζ0 = 13.54 for the Turing pattern generated during the decrease of ωp, while ζ0 = 23.89 for the single soliton state generated during the increase of ωp.

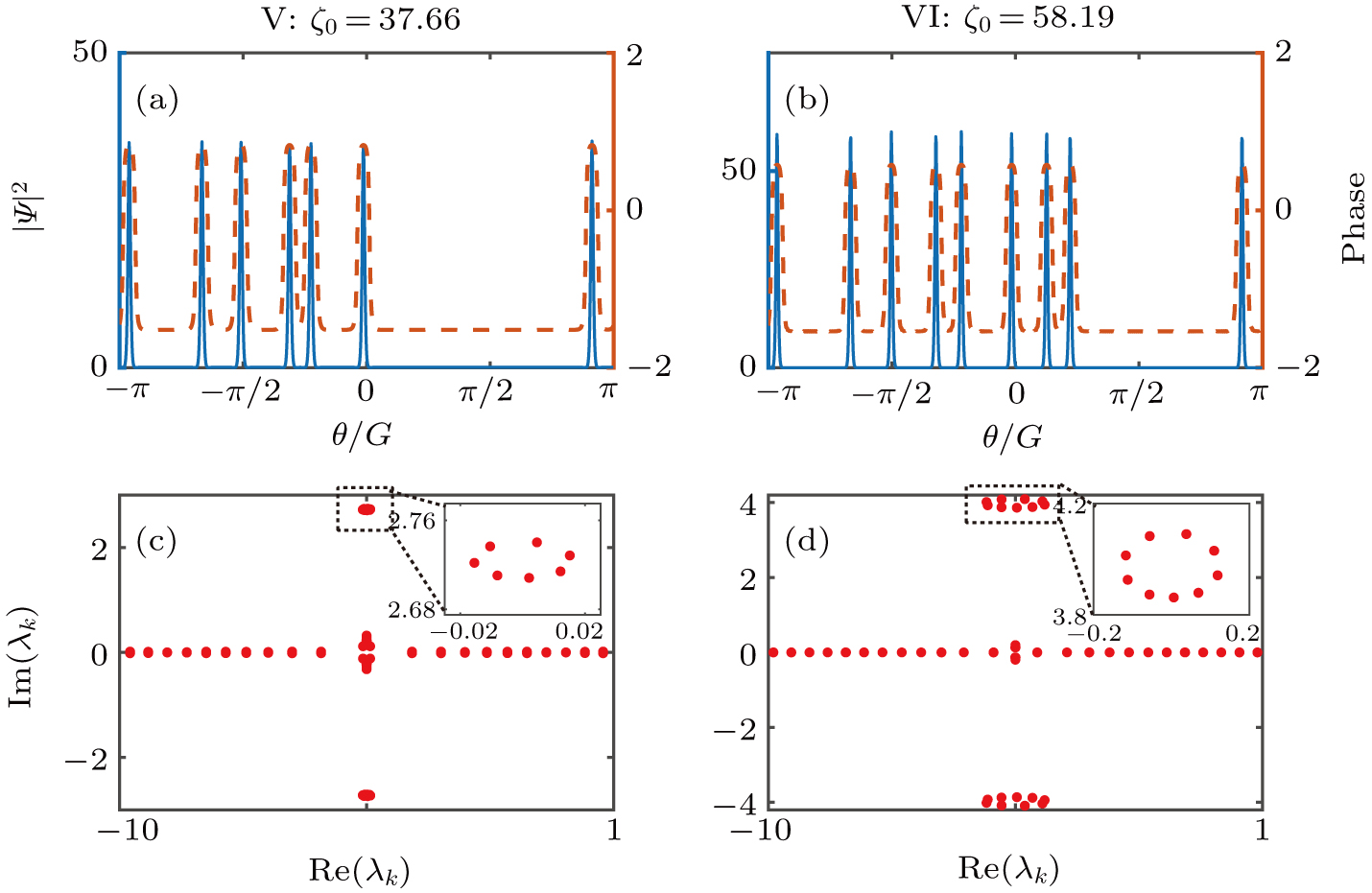
Then we analyze the chaotic and multi-solitons temporal signals. The temporal characteristics for the chaos and 4-solitons state are captured as Fig. 6 shows, as well as their frequency characteristics. The time-domain signal of 4-solitons here is non-periodic in a round trip time, that is, the distance between the 4 solitons is not equal. So, its linear spectrum (Fig. 6(d)) is very similar to that of the chaos (Fig. 6(c)), they both look very noisy, and thus the multi-solitons state may sometimes be mistaken as chaotic states just by identifying the linear spectrum. In essence, however, they are significantly different from each other. That is, the modes of chaotic OFCs are incoherent, so the comb is unstable, whereas the multi-solitons comb is generally stable. Based on the NFT analysis of the two time-domain signals in Figs. 6(a) and 6(b), the nonlinear eigenvalue spectra are obtained as shown in Figs. 6(e) and 6(f). As mentioned above, the eigenvalue spectrum of chaos is also chaotic, while the eigenvalue spectrum of the 4-solitons signal is actually ordered because of the strict symmetry of the discrete eigenvalues arisen from its radiation components, which ensures a good distinction between the multi-solitons signal and chaotic signal. We can also observe 4 pairs of obvious isolated eigenvalues in Fig. 6(f) corresponding to the signal's soliton components, and the number of solitons in the temporal pulse is also 4. It should be noted that we have carried the proper adjustments to the signal amplitude in the multi-solitons case to capture the signal in the form of soliton components A sech (At) as close as possible for further NFT analysis.

Fig. 6. The temporal intensity and phase profiles, linear spectrum, and nonlinear eigenvalue spectrum of chaos (left column) and 4-solitons state (right column). ζ0 = 35.16 for the chaos generated during the decrease of ωp, while ζ0 = 27.34 for the 4-solitons state generated during the increase of ωp.

We also perform the periodic nonlinear Fourier transform analysis of 7-solitons and 9-solitons signals, and obtain the nonlinear eigenvalue spectra as shown in Fig. 7. By adjusting the amplitude of the signal extracted from the temporal evolution, the corresponding soliton eigenvalues and non-soliton eigenvalues separate well in the eigenvalue spectrum. For a more intuitive view, partial eigenvalue spectra for 7-solitons and 9-solitons are presented and thus we just focus on the distribution of isolated soliton eigenvalues. We also find that the number of isolated eigenvalue pairs corresponds to the number of solitons in the time domain, that is, there are 7 pairs of distinct isolated eigenvalues for the 7-solitons temporal signal and 9 pairs for the 9-solitons state.

Fig. 7. The temporal intensity and phase profiles, and nonlinear eigenvalue spectrum of 7-solitons (left column) and 9-solitons states (right column). ζ0 = 37.66 for 7-solitons state and ζ0 = 58.19 for 9-solitons state are both generated during the increase of ωp.
4. Conclusion

In summary, based on the fact that the normalized LLE can be regarded as the NLSE including several other effects, we can apply periodic NFT to the analysis of signals during the generation of OFCs in the Kerr microresonator. We finally find that the signals at different states can be distinguished clearly according to different distributions of the eigenvalue spectrum. For the time-domain signal extracted from a chaotic state, its eigenvalue distribution is also disordered. The eigenvalue spectrum of the Turing pattern is characterized by several strictly symmetric isolated eigenvalue pairs. Specially, the eigenvalue spectrum of the single soliton pulse is composed of a pair of conjugate symmetric isolated eigenvalues and the quasi-continuous eigenvalue spectrum with eye-like structure. Take NFT analysis directly for the multi-solitons time-domain signal in the cavity, the eigenvalue spectrum obtained is complex but ordered. By adjusting the signal amplitude, we can approximately capture the waveforms corresponding to the soliton components. In this way, obvious soliton eigenvalue pairs are obtained by NFT and its number is consistent with the number of solitons formed in the microresonator.

In this work, we have discovered that there is a certain correlation between the nonlinear eigenvalue spectrum and the linear spectrum. However, the accurate correspondence needs to be studied in the future. And we hope to derive the mathematical form of amplitude adjustment in the case of multi-solitons from the expression of soliton solution in Kerr microresonator in next work for richer soliton dynamics analysis.

Reference
[1] Yousefi M I Kschischang F R 2014 IEEE Trans. Inf. Theory 60 4312
[2] Agrawal G P 2007 Nonlinear Fiber Optics 4 Academic Press https://www.sciencedirect.com/book/9780123695161/nonlinear-fiber-optics
[3] Prilepsky J E Derevyanko S A Blow K J Gabitov I Turitsyn S K 2014 Phys. Rev. Lett. 113 013901 https://www.researchgate.net/publication/263622018_Nonlinear_Inverse_Synthesis_and_Eigenvalue_Division_Multiplexing_in_Optical_Fiber_Channels
[4] Yousefi M I Kschischang F R 2014 IEEE Trans. Inf. Theory 60 4346
[5] Wang L N Liu S Y Li C Y He G Q 2017 A Combination of Eigenvalue and Spectral Function Modulation in Nonlinear Frequency Division Multiplexing OSA Nonlinear Optics Toptical Meeting (NLO), 17–21 July 2017 Waikoloa, Hawaii, USA 10.1364/NLO.2017.NW4A.21
[6] Liu S Y Wang L N Li C Y He G Q 2017 Spectral Function Modulation based on Nonlinear Fourier Transform OSA Nonlinear Optics Toptical Meeting (NLO), 17–21 July 2017 Waikoloa, Hawaii, USA https://doi.org/10.1364/NLO.2017.NW4A.22
[7] He G Q Wang L N Li C Y Liu S Y Hu W S 2017 Sci. Rep. 7 6058
[8] Son T Le Aref V Buelow H 2017 Nat. Photon. 11 570
[9] Son T Le Buelow H 2017 IEEE J. Lightwave Technol. 35 3692
[10] Gui T Lu C Lau A P T Wai P K A 2017 Opt. Express 25 20286 https://www.osapublishing.org/oe/abstract.cfm?uri=oe-25-17-20286
[11] Goossens J W Yousefi M I Jaouën Y Hafermann H 2017 Opt. Express 25 26437 https://www.osapublishing.org/oe/abstract.cfm?uri=oe-25-22-26437&origin=search
[12] Son T Le Aref V Buelow H 2018 IEEE J. Lightwave Technol. 36 1296
[13] Son T Le Schuh K Buchali F Buelow H 2018 Optical Fiber Communication Conference paper W1G.6 https://www.osapublishing.org/abstract.cfm?uri=ofc-2018-W1G.6&origin=search
[14] Yangzhang X Aref V Son T Le Buelow H Bayvel P 2018 arXiv:1806.10367v1 https://www.researchgate.net/publication/326029740_400_Gbps_Dual-polarisation_Non-linear_Frequency-division_Multiplexed_Transmission_with_b-Modulation
[15] Wang J Zhao Y L Huang X He G Q 2019 ZTE Commun. 3 17
[16] Ryczkowski P Närhi M Billet C Merolla J M Genty G Dudley J M 2018 Nat. Photon. 12 221
[17] Kippenberg T J Gaeta A L Lipson M Gorodetsky M L 2018 Science 361 567
[18] Godey C Balakireva I V Coillet A Chembo Y K 2014 Phys. Rev. A 89 063814 https://journals.aps.org/pra/abstract/10.1103/PhysRevA.89.063814
[19] Chembo Y K Menyuk C R 2013 Phys. Rev. A 87 053852 https://journals.aps.org/pra/abstract/10.1103/PhysRevA.87.053852
[20] Lamont M R E Okawachi Y Gaeta A L 2013 Opt. Lett. 38 3478
[21] Herr T Brasch V Jost J D Wang C Y Kondratiev N M Gorodetsky M L Kippenberg T J 2014 Nat. Photon. 8 145
[22] Guo H Karpov M Lucas E Kordts A Pfeiffer M H P Brasch V Lihachev G Lobanov V E Gorodetsky M L Kippenberg T J 2017 Nat. Phys. 13 94
[23] Wahls S Poor H V 2015 IEEE Trans. Inf. Theory 61 6957
[24] Yousefi M I Kschischang F R 2014 IEEE Trans. Inf. Theory 60 4329
[25] Agha I H Okawachi Y Gaeta A L 2009 Opt. Express 17 16209 https://www.osapublishing.org/oe/abstract.cfm?uri=oe-17-18-16209
[26] Turitsyn S K Prilepsky J E Son T Le Wahls S Frumin L L Kamalian M Derevyanko S K 2017 Optica 4 307
[27] Matsuda Y Terauchi H Maruta A 2014 OptoElectronics and Communication Conference 1016 https://ieeexplore.ieee.org/document/6888356?arnumber=6888356&tag=1