† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11404040) and Qing Lan Project of the Higher Educations of Jiangsu Province of China.
We theoretically investigate the quantum enhanced metrology using two-mode squeezed twin-Fock states and parity detection. Our results indicate that, for a given initial squeezing parameter, compared with the two-mode squeezed vacuum state, both phase sensitivity and resolution can be enhanced when the two-mode squeezed twin-Fock state is considered as an input state of a Mach–Zehnder interferometer. Within a constraint on the total photon number, although the two-mode squeezed vacuum state gives the better phase sensitivity when the phase shift φ to be estimated approaches to zero, the phase sensitivity offered by these non-Gaussian entangled Gaussian states is relatively stable with respect to the phase shift itself. When the phase shift slightly deviates from φ = 0, the phase sensitivity can be still enhanced by the two-mode squeezed twin-Fock state over a broad range of the total mean photon number where the phase uncertainty is still below the quantum standard noise limit. Finally, we numerically prove that the quantum Cramér–Rao bound can be approached with the parity detection.
Optical interferometers are important devices in quantum metrology. Mach–Zehnder interferometers (MZIs) and SU(1,1) interferometers[1–6] are two kinds of basic optical interferometers, which are widely used to measure an unknown phase shift in the two arms of an interferometer and its phase sensitivity Δφ. In general, the precision of phase estimation within these settings crucially depends on the input states as well as the detection schemes. It is well known that nonclassical quantum states, such as the squeezed state and the Fock state, are the most key resources to improve the precision of phase estimation in an interferometer. In a lossless MZI, a few decades ago Caves[2] demonstrated that the sensitivity of phase estimation using the coherent light together with the squeezed vacuum one could beat the standard quantum noise limit (SNL), namely, 


In recent years, many other nonclassical states have been studied to improve the precision of phase estimation based on an MZI.[9–18] For example, an MZI with the N00N state can offer the HL limit in principle.[9,10] Unfortunately, ideal N00N states are challenged to generate in experiments and these states are extremely fragile.[11,12] Another way to approach the HL limit is through the injection of the twin-Fock state |n,n⟩ into the first beam splitter of an MZI.[13] Compared with the N00N state, the twin-Fock state is easier to generate and more robust against photon loss.[6,14–17] Therefore, the twin-Fock state is traditionally used to approximate the N00N state. Especially, in the case of the input twin-Fock state |n,n⟩ with two photons (n=1), the state inside the interferometer after the first beam splitter is just a N00N state. In addition, it has been proved that the twin-Fock state with six photons can be prepared in experiments using photon pairs from spontaneous parametric down conversion.[15,16] As continuous-variable superpositions of twin-Fock states, it is found that an MZI with a two-mode squeezed vacuum state (TMSVS) and parity detection can offer the sub-Heisenberg sensitivity.[19] However, it is difficult to prepare these Gaussian entangled states with a large mean photon number. In experiments, the largest achievable total photon number of the TMSVS so far is about 4 in a stable optical configuration, and the corresponding squeezing parameter is about r ≈ 1.15 (i.e., about 10 dB).[20] On the other hand, Gerry and Mimih[21] showed that the phase sensitivity for these entangled Gaussian states is very unstable with respect to the phase shift itself. When the phase shift moderately deviates from the optimal values of the phase shift (for example, φ = 0), the phase sensitivity will rapidly becomes worse, even above the SNL. To remedy these problems, the non-Gaussian entangled states, such as photon-subtracted TMSVS[22,23] and photon-added TMSVS,[24] have been used to improve the precision of phase estimation based on an MZI with parity detection.
Besides the photon-subtracted or photon-added TMSVS, two-mode squeezed number states are also a broad and meaningful class of continuous-variable non-Gaussian entangled states. Such states were originally introduced by Chizhow,[25] where the photon number statistics and the phase properties have been investigated. The analysis of their inseparabilities was also carried out via the Neumann entropy.[26,27] It has shown that, for a given initial squeezing, the two-mode squeezed number state with a higher number state has a larger amount of entanglement. Very recently, non-Gaussianity dynamics of such states has also been studied.[28] In this work, we investigate the applications of the two-mode squeezed number states on the quantum enhanced metrology. In many applications, pair creation occurs starting from the vacuum. Therefore, here we mainly consider the two-mode squeezed twin-Fock state (TMSTFS) as the input state of an MZI, and investigate the performance of the TMSTFS on phase estimation via both quantum Fisher information and parity detection. Theoretically, a TMSTFS is obtained by applying a two-mode squeezed operator 

The remainder of this paper is organized as follows. Section 
Following the work in Ref. [29], the TMSTFS can be considered as the TMSVS excited by the Laguerre polynomials operator, i.e.,

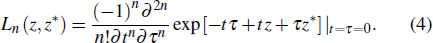
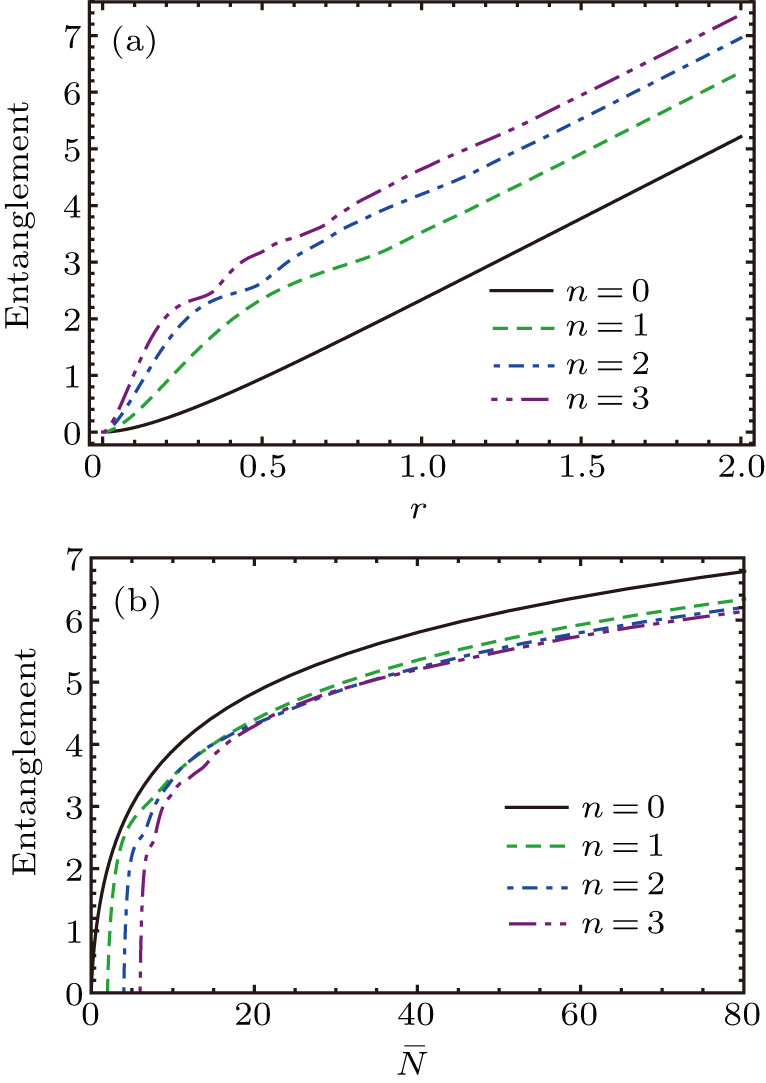
Although entanglement is not a critical resource for quantum-enhanced metrology,[30,31] entangled photon number states are indeed helpful for phase estimation.[9,10,32] For our purpose, let us review the von Neumann entropy of the TMSTFS.[27] For a pure state in the Schmidt decomposed form, the quantum entanglement is characterized by the partial von Neumann entropy.[33] Based on Eq. (
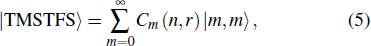


Here we consider an balanced MZI interferometer whose two input ports are fed by the TMSTFS as shown in Fig.
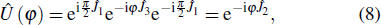

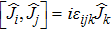
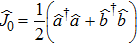
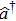

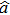

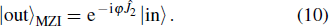
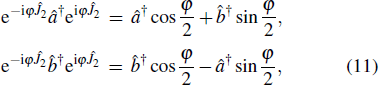

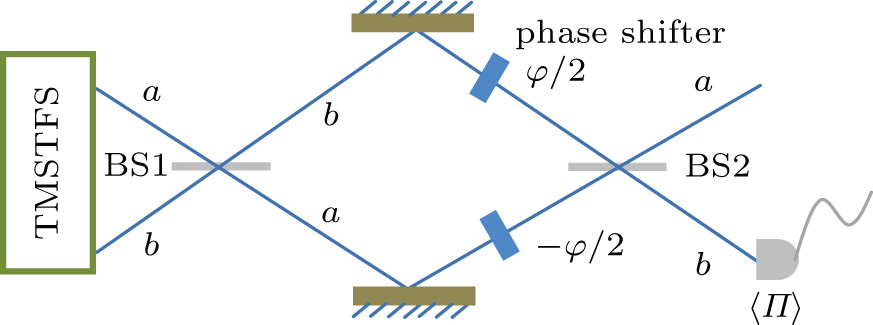 | Fig. 2. The Mach–Zehnder interferometer used for the detection of the phase shift when the TMSTFS is injected into the first beam splitter. |
In this section, we investigate the QCRB, which gives an ultimate limit to the precision of phase sensitivity for all possible locally unbiased estimators and the most general measurements, which is expressed by the quantum Fisher information,[34] i.e.,
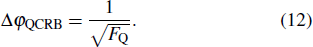
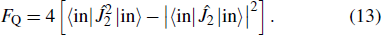
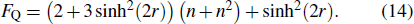


In the above discussion, we have investigated the phase sensitivity limit based on direct calculation of the quantum Fisher information. In the following, we show that the QCRB Δφmin can be reached with the parity detection in the case φ → 0. Actually, for a certain type of path-symmetric states, the detection of photon number parity can achieve the QCRB at particular values of phase shift φ.[36] For the TMSTFS considered as an interferometer state, we can prove that both homodyne detection[37–39] and intensity detection[40–43] are not suitable for the phase estimation. Therefore, in the work we mainly consider the parity detection as our measuring scheme.
For the convenience of the calculation, it is useful to expand the TMSTFS in the basis of the coherent state,


Parity detection is actually to perform photon number parity measurements on just one of the output modes of the MZI. The parity operator for the b mode can be expressed by[44]
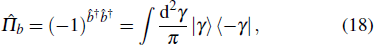


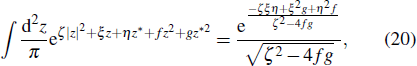
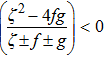
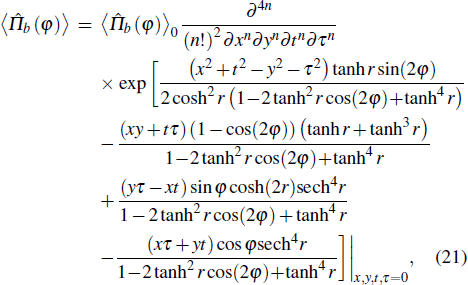

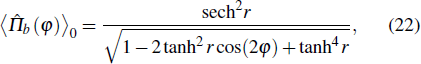
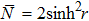

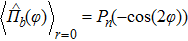

Now we turn to investigate the phase sensitivity (or phase uncertainty) of the parity detection based on the classical Fisher information. For the parity detection, there are only two outcomes, e for even and o for odd. According to the concept, the classical Fisher information FC for parity detection is given by[36]
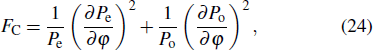



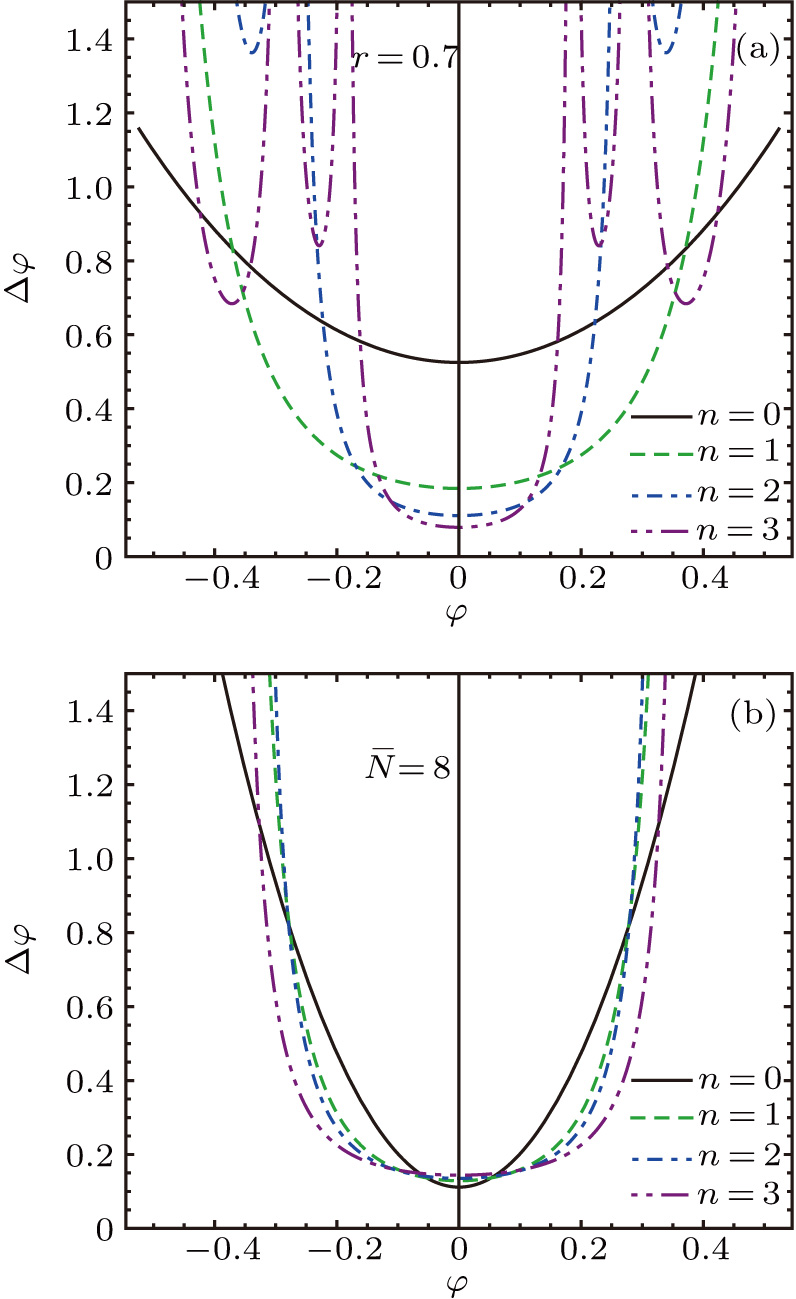 | Fig. 4. Phase sensitivity Δφ as a function of the phase shift φ for some different values of n: (a) for a given initial squeezing parameter, r = 0.7; (b) for a given total mean photon number, 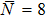 |
In Fig.
 | Fig. 5. Phase sensitivity Δφ as a function of the initial squeezing parameter r for different values of n at φ = 10−3. |
In this work, we have investigated theoretically the performance of the TMSTFS on the quantum enhanced metrology. Via parity detection and quantum Fisher information, our results show that, compared with the TMSVS, both phase resolution and phase sensitivity can be enhanced by the TMSTFS for a given initial squeezing parameter. On the other hand, within a constraint on the total photon number, the TMSVS gives the better QCRB. These results are similar to the properties of the quantum entanglement of the TMSTFS. However, via parity detection, the phase sensitivity offered by the TMSVS will rapidly becomes worse, even above the SNL, when the phase shift moderately deviates from φ = 0. This is in marked contrast to what happens for the TMSTFS, which are relatively stable in that sense. That is to say, when the phase shift slightly deviates from zero, the TMSTFS can give the better phase sensitivity over a broad range of the total photon number where the phase uncertainty is still below the SNL, even under energy constraint. Therefore, compared with the TMSVS, the phase sensitivity can be indeed enhanced by the TMSTFS on some different occasions. These results are useful towards a complete understanding of quantum non-Gaussian states for quantum informatics. Finally, we show that the QCRB can be approached via the parity detection for the TMSTFS when the phase shift comes nearly to zero.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] |