Great attention has been paid to three-dimensional (3D) Dirac semimetals, also called bulk Dirac semimetals (BDSs), due to the recent experimental discovery of Cd₃As₂,^[1–3] Na₃Bi,^[4] and ZrTe₅.^[5] As confirmed by angle-resolved photoemission spectroscopy, BDSs are characterized by a linear dispersion relationship for fermion quasiparticles along all three momentum directions, and thus they can be viewed as 3D counterparts to graphene. Graphene has demonstrated to have great potential in the application of subwavelength plasmonic devices.^[6–11] Surface plasmon polaritons (SPPs) that are supported on graphene have the properties of extremely high confinement and low Ohmic loss because of their large carrier mobility.^[6,12,13] As types of 3D graphene, BDSs can also sustain SPPs in the terahertz (THz) to mid-infrared regimes. The much higher mobility of BDSs, arising from the crystalline symmetry protection against gap formation,^[14] may lead to advances in SPPs properties. Additionally, an extra dimension brings essential differences to some property of the SPPs, i.e., the SPP-coupling between the interfaces of the BDS film results in the splitting of the SPP dispersion into symmetric and asymmetric modes, and the characteristics of SPPs are influenced by the thickness of the BDS film.^[15] Recently, intense study of the plasmon mode arising in BDSs has been carried out,^[16–20] and some unique features have been uncovered.^[16,17]

In the past few decades, THz radiation has become the most attractive research area in modern science and technology due to its unique characteristics and wide potential applications.^[21–24] However, the development of room temperature, miniature, high powered and tunable THz radiation sources covering the entire THz frequency regime remains a significant challenge. Recently, free-electrons driven graphene plasmonics have provided exciting opportunities for THz radiation sources.^[25–31] The desired THz radiation can be developed mainly depending on the remarkable properties of graphene SPPs. The well-known wavevector mismatch between SPPs and electromagnetic waves in free-space prevents direct SPP-radiation coupling. To compensate for this momentum mismatch, particular effects are needed, such as periodic zone folding,^[25–27] nonlinearity,^[28] circular periodicity,^[29] sidewall,^[30] and buffer layer effects.^[31] In these works, the diffraction radiation or Cherenkov radiation mechanisms were involved. The radiation intensity of the Cherenkov effect was two to three orders of magnitude higher than that of diffraction radiation.^[29,31]

In this article, we present a physical mechanism in which coherent and tunable THz radiation can be generated from SPPs excited by a moving electron beam on top of a BDS film deposited on a dielectric substrate. Due to the SPP-coupling between the interfaces of the film, the SPP dispersion splits into symmetric and asymmetric modes, and the energy of the asymmetric SPP mode is greatly enhanced to cross the light line of the substrate, thus, making the transformation of the SPPs into radiation immediately possible. Two-color THz radiation can be generated from symmetric and asymmetric SPP modes when a buffer layer with a lower permittivity relative to the substrate is introduced. Compared to the radiation without SPPs, the radiation intensity is enhanced by SPPs by over two orders up to 6.7 × 10⁴ W/cm². The radiation frequency can be tuned in the THz frequency band by varying the energy of the electron beam and the chemical potential of the BDSs.

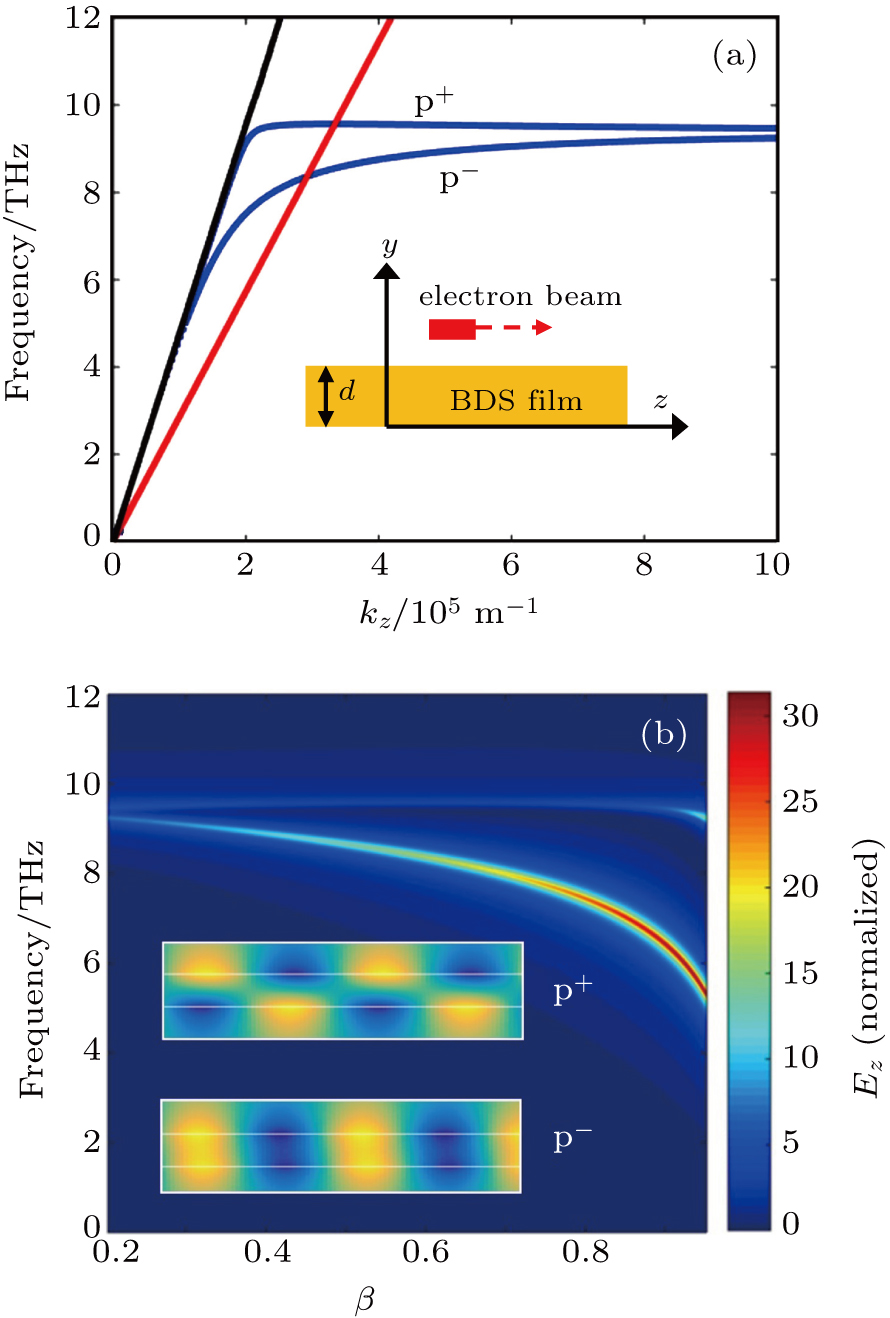
We first considered the SPPs excitation by an electron beam moving on top of a BDS film suspended in vacuum, as shown in the inset of Fig. 1(a). The conductivity of the BDSs derived with the Kubo formalism is given as^[15]

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. (a) The dispersion curves of a suspending BDS film excited by an electron beam. The solid red line is the dispersion curve of a moving electron beam. The parameters: d = 2 μm, ε∞ = 13, g = 4, T = 300 K, τ = 1.2 ps, vF = 0.9 × 106 m/s, and μc = 0.1 eV. (b) The dependence of the frequencies and field amplitudes of the excited SPPs on the beam energy. The inset is the electric field distributions of asymmetric SPP mode and symmetric SPP mode.

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. (a) Schematic diagram of an electron bunch moving on top of a BDS film deposited on a dielectric substrate. (b) The dispersion curves. The solid red line represents the dispersion curve of a moving electron beam. (c) Fourier spectra of the radiation intensity. (d) The contour map of the electric field intensity Ez in the y–z plane. The beam velocity was 0.4c, the permittivity of the substrate was 12, and the distance between the electron beam and the surface of the BDS film was y0 = 0.1 μm. The other parameters were the same as those used in Fig. 1.

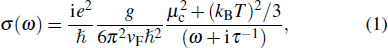
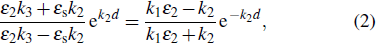
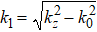
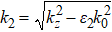
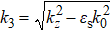
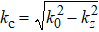
Based on the dispersion Eqs. (3) and (4), the dispersion curves of a suspending BDS film were calculated, as shown in Fig. 1(a). Both of the symmetric (p⁻) and asymmetric (p⁺) modes were located on the right side of the light line (the black solid line), which indicated that the direct light-SPP or SPP-light couplings were impossible. Fortunately, the large wavevector of the evanescent waves generated by a moving electron beam (k_z = k₀/v, v is the velocity of electron beam) could match that of the SPPs at the intersection points between their dispersion curves. Thus, a moving electron beam could directly excite coherent SPP modes. The frequency of the SPPs could be tuned by adjusting the beam energy. Figure 1(b) shows the dependence of the amplitude of the E_z fields (normalized by the field amplitude of the evanescent waves generated by the electron beam) and the frequencies of the two SPPs modes for the velocity of the electron beam β(v/c). Both of the two SPP modes could be efficiently excited by an electron beam, and the excitation for the symmetric SPP mode in the low frequency range was much stronger due to the lower intrinsic loss.

We have demonstrated the efficient excitation of SPPs in BDS film by an electron beam. Now we will show the transformation of SPP into THz radiation in a structure of BDS film with a dielectric substrate loading, as depicted in Fig. 2(a). Based on the dispersion Eq. (2), the dispersion curves of the structure are shown in Fig. 2(b). The shaded region bounded by the light lines in vacuum and dielectric (the two solid black lines) is the Cherenkov radiation zone. The coupling of the SPP between the interfaces of the BDS film greatly enhanced the energy of the asymmetric SPP mode to enter into the radiation zone, so the excited SPPs could be directly transformed into radiation. The symmetric SPP mode was always below the dielectric light line, thus, it could not be transformed. The beam line with velocity of 0.4c intersected with the dispersion curve of the asymmetric mode at point A. The radiation spectrum (calculated using Eq. (7)) shown in Fig. 2(c) has a peak at the SPP resonance frequency 9.4 THz corresponding to point A. The E_z field distribution shown in Fig. 2(d) indicates the process of transforming the SPPs into radiation. The SPPs were first excited by the moving electron beam; and then transformed into Cherenkov radiation in the substrate. The radiation angle, calculated by equation , equals 137.6°.

The symmetric SPP mode could not be transformed into radiation because its dispersion curve always lay below the light line in the dielectric substrate. We added a dielectric buffer layer with a thickness h between the BDS film and the substrate, as shown in Fig. 3(a). For the case of buffer layer with a lower permittivity compared to the substrate, the transformation of the symmetric SPP mode into radiation could become possible. The dispersion relation of the SPP modes could also be obtained by making use of Maxwell’s equations and the boundary conditions

Fig. 3.

Figure Option ViewDownloadNew Window

Fig. 3. (a) Schematic diagram of an electron bunch moving on top of a BDS film deposited on a dielectric substrate with a buffer layer. (b) The dispersion curves. The inset shows the Fourier spectra of the radiation intensity. The contour map of the electric field intensity Ez in the y–z plane at the frequencies of (c) 7.68 THz and (d) 9.44 THz. The thickness of the buffer layer h was 2 μm, and the permittivity of the buffer layer was 2.25. The other parameters were the same as those used in Fig. 2.

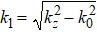
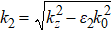
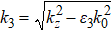
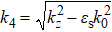
The dispersion curves of the structure with a buffer layer based on the dispersion Eq. (8) are shown in Fig. 3(b). Compared to the dispersion curves in Fig. 2(b), the dispersion of the symmetric mode shifted upward, crossing the light line in the substrate, thus, it could also be transformed into radiation. The energy shift of the symmetric SPP mode contributed to the buffer layer. With the buffer layer, the SPP dispersion was bounded by the light line of the buffer layer rather than by the light line of the substrate. If the buffer layer had low permittivity relative to the substrate, the dispersion of the SPPs would be lifted to exceed the light line of the substrate. The beam line with a velocity of 0.4c could intersect with the two SPPs modes at points B and C in the radiation zone. Thus, two-color THz radiation could be generated simultaneously. The radiation spectra are shown in the inset of Fig. 3(b). There were two radiation frequencies, 7.68 THz and 9.44 THz, corresponding to the intersection points B and C. The field distributions shown in Figs. 3(c) and 3(d) indicated little difference of the transformation process compared to that in the structure without a buffer layer. With the buffer layer, the excited SPPs could not be directly transformed, They would penetrate the buffer layer to reach the dielectric–substrate interface, and then transform into Cherenkov radiation in the substrate. To guarantee the high efficiency of transformation of SPPs into radiation, the thickness of buffer layer should be in the order of the decay length.

The radiation intensity was significantly enhanced by the excited SPPs. It should be pointed out that, without the excitation of the SPPs, Cherenkov radiation could also occur. It was transformed from the evanescent wave generated by the electron beam when the wave-phase velocity was greater than that of the light in the substrate. For the symmetric SPP mode, the enhancement was greater by a factor of 263. The underlying physics of the large enhancement meant that the intensity of the excited SPPs was two or three orders higher than that of the evanescent wave. The power density could be evaluated by the method proposed in Refs. [26,31] The radiation power density was proportional to the square of the charge density of the electron beam.^[31] For a charge density of 100 pC/cm, the peak radiation power density could reach 6.7 × 10⁴ W/cm². This was comparable to the radiation from graphene SPPs.

The experimental work demonstrated the stability of the bulk Dirac fermion since the chemical potential was tuned by surface doping.^[4] The dependence of the radiation frequency on the chemical potential and beam energy is shown in Fig. 4. We focued on the symmetric mode due to its excellent tunability. The dispersion curves in Fig. 3(b) indicate that increasing the beam energy leads to a lower frequency THz radiation. This was because the higher energy electrons could provide a smaller wavevector for the SPPs corresponding to a longer wavelength. For a fixed chemical potential, the radiation frequency could be continuously tuned in a wide THz range by adjusting the beam energy. As the chemical potential increased, the radiation frequency increased and the tunable frequency band became wider. Due to the surface plasmon frequency being linearly proportional to the chemical potential,^[17] the SPP energy increased with the increasing chemical potential, higher radiation frequency, and broader tunable frequency band.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. The radiation frequency versus the chemical potential and the beam energy β (the ratio of the electron velocity to the speed of light).

We presented a physical mechanism of THz generation from SPPs in the structures of BDS film deposited on a dielectric substrate with or without a buffer layer. We found that the asymmetric SPP mode could cross the light line of the substrate due to the dramatically increased energy of the SPPs caused by the splitting of the SPP dispersion. The dispersion of the symmetric SPP mode could also be lifted to cross the light line in the substrate by a buffer layer with a lower permittivity relative to the substrate. Based on these mechanisms, one-color or two-color THz radiation from SPPs excited by a moving electron beam atop BDS film was analyzed. The results showed that the radiation intensity was significantly enhanced over 200 times up to 6.7 × 10⁴ W/cm². Furthermore, the radiation frequency could be tuned in the THz frequency regime by adjusting the beam energy or the chemical potential of the BDSs. Based on this mechanism, the room temperature, tunable, coherent, and intense THz radiation sources could be developed.