Electron–ion recombination is one of the most fundamental atomic collision processes, and plays an important role in plasma physics, astrophysics as well as accelerator physics.^[1] The experimentally obtained electron–ion recombination rate coefficients can be not only used to study the energy level structure of highly charged ions, thereby testing the theoretical methods for atomic structures calculation, but also used as the basic input parameters for plasma diagnosis and modeling to interpret the emission spectrum of astrophysical and man-made plasmas.^[2] Additionally, the electron–ion recombination also reduces the lifetime of the ion beam which leads to the positive ions loss mechanism during electron cooling, particularly at high ion charge state and high beam velocity when the residual gas processes become less important.^[3] The electron–ion recombination with its large cross section and rates at the low energies also provides a very favorable scheme for the production of antihydrogen.^[4] However, most of these electron–ion recombination cross sections are calculated by different theories with limited accuracy, and experimental studies to benchmark these theories are very important and have been already investigated for decades. There are two most dominating electron–ion recombination channels for low energy collision range called radiative recombination (RR) and dielectronic recombination (DR). The RR is a one-step non-resonant process where a free electron recombines with an ion by simultaneously emitting a photon to release the excess energy

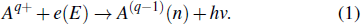
The first radiative recombination experiment at low energy was performed by merging C⁶⁺ ion beam with an electron beam in a single pass arrangement by Andersen et al.^[6] In that experiment a good agreement has been found between measured recombination rates and calculated results in the energy range from E_rel = 0 eV to 1 eV, where E_rel is the relative collision energy between electrons and ions. However, a significant enhancement effect beyond the theoretical calculation has been found in a range of low relative energies between electron and ions in the RR experiments. In order to understand this rate enhancement phenomenon, a series of electron–ion recombination experiments with many bare ions (D⁺, He²⁺, C⁶⁺, N⁷⁺, Ne¹⁰⁺, Si¹⁴⁺, Ar¹⁸⁺, Bi⁸³⁺) have been performed to investigate this RR enhancement effect at different storage rings.^[5,7–13] These works test the variation of electron beam density,^[14] the influence of magnetic field,^[5] and also the dependence of charge state.^[9] Strong enhancement effects have been observed for all of these measured RR rate coefficients as compared with the theoretical rate coefficients at a very low electron–ion collision energies (E_rel < 10 meV).

In addition to the bare-ions, the RR rate enhancement has also been observed in experiments with non-bare ions at the storage rings.^[15–19] However, because of the complex electronic structure of non-bare ions, neither a concentrated study is available for these enhanced rates, nor have detailed quantitative spectra in low relative energy region have been presented. To explain this surprising discrepancy between the measured RR recombination rate coefficients and the theoretical predictions, several theoretical models and mechanisms have been proposed ranging from the contributions from three body recombination (TBR),^[9] the electron density enhancement in the surrounding of the ions due to plasma screening effect^[20] and the effect of magnetic field taking into account the chaotic dynamic as a result of the magnetic field inside the electron cooler which directly influence the cross sections.^[21] Some of the models also included the contribution of transient field effects by a magnetic field in the electron-cooler^[22] and relativistic effects by using Dirac–Slater method together with multichannel quantum defect theory (MQDT).^[23,24] Finally, one model by taking into account of the transient field effects from a magnetic field explained the observed RR enhancement phenomenon with only bare ions.^[25]

An approach presented in this work is mainly focused on the investigation of RR rate enhancement in electron–ion recombination spectra for non-bare highly charged ions. Recombination of Ar¹⁴⁺, Ar¹⁵⁺, Ca¹⁶⁺, and Ni¹⁹⁺ ions with electrons at low energy range have been investigated based on the merged-beam method at the main cooler storage ring CSRm. In order to interpret the measured results, RR cross sections were obtained from a modified version of the semi-classical Bethe and Salpeter formula for hydrogenic ions. DR cross sections were calculated by a relativistic configuration interaction method using the flexible atomic code (FAC) and AUTOSTRUCTURE code in this energy range. The calculated total rate coefficients show a good agreement with the measured rate coefficients above 100 meV. However, large discrepancies have been found at the low energy range especially below 10 meV. As the relative collision energy decreases below 1 meV, it is found that the observed recombination rates are a factor of 1.5 to 3.9 higher than the predicted rates. The dependence of RR rate coefficient enhancement as a function of the charge state of the ions has been obtained and compared with bare ions.

The article is arranged as follow. In Section 2 we will discuss the experimental set up and methods regarding to the merged beams electron–ion recombination at the CSRm with some important parameters. Section 3 will briefly describe the theoretical approach related to RR and DR, with the modified semi-classical Bethe and Salpeter formula for RR and the AUTOSTRUCTURE and FAC codes implementation for DR. Section 4 presents the experimental results and comparison with the current calculations. Additionally, the experimental data are scaled as a function of the nuclear charge state of the ions and also compared with different results from literature. Section 5 is concerning with the conclusion of the present work.

The measurement of electron–ion recombination with highly charged ions has been performed by employing the merged beams method at the CSRm at Institute of Modern Physics (IMP) in Lanzhou, China (See Fig. 1). The main features of the experimental technique were described in the previous papers and Refs. [26–28]. Here we will just briefly describe the general experimental method and important parameters related to the present work. The highly charged ions were produced in the ECR ion sources,^[29] and then supplied by a sector focused cyclotron (SFC) to the CSRm after acceleration. One injection pulse of ions from the SFC into CSRm was enough to provide the typical ion current of 50 μA–150 μA which corresponds to the number of ions 1 × 10⁸–3 × 10⁸. The ion beam lifetime is around 50 s. The ion-beam was merged with the magnetically confined electron-beam of the cooler in one straight section with typical length of 4.0 m of the CSRm storage ring.

Fig. 1.

Figure Option ViewDownloadNew Window

Fig. 1. The schematic view of the electron cooler and the experimental setup for electron–ion recombination experiment at the CSRm, Lanzhou. The electron beam produced at the cathode is guided by magnetic field, then merges with ion beam at the straight section of 4.0 m. The electron-beam is then separated from the ion-beam by the magnetic guiding field and collected by the anode. In a dipole magnet downstream to the electron cooler the recombined ions are separated from the primary ion beam, and then counted by a scintillator detector.

The ion beams have been cooled for several seconds by employing electron cooler (EC-35) before starting a measurement until the beam profile reached to their equilibrium spread. The electron-beam was confined at the cathode section of the electron cooler with magnetic field of 125 mT and adiabatically expanded at the cooler section with 39 mT, respectively. This expansion gives rise to cold electron beam for high resolution spectroscopy. The magnetically confined electron beam at the cooler section has a radius of ∼ 25 mm, with a typical electron density of 1 × 10⁶ cm⁻³. Besides electron cooling, the electron cooler is also used as an electron target during the electron–ion recombination measurement. For a change of the electrons energy from cooling energy, the detuning system has been applied to the cathode of the electron cooler. For introducing non-zero mean relative velocities between the electrons and ions, the electron energy was stepped through a preset range of values different from the cooling energy during the measurement cycle. The measurement cycle includes different detuning voltages of 1 V in laboratory system. In each measurement interval, the electron energy was detuned for 10 ms and again set to the cooling energy (E_rel = 0) for 90 ms or 190 ms in order to maintain a good ion-beam quality. The recombined ions formed in the merging section were separated by the first dipole magnet downstream the electron cooler and detected by a scintillator detector.^[30]

At storage rings, the recombination rate coefficients α measured at scanning energy E_rel, between electron and ion is determined by

The calculation of the RR cross section is based on the modified semi-classical formula of Bethe & Salpeter in this work. RR of high-Z bare ions with cold electrons can be treated within the non-relativistic dipole approximation. Bethe and Salpeter derived a simple formula for RR cross section calculation,^[32]

In the present experiments all of the ions which have been measured are non-bare and the contribution from DR resonance process could not be avoided. Therefore, the DR process must be considered in the theoretical calculations for better investigation of the electron–ion recombination spectra at very low energy range. The theoretical calculations of DR for Be-like Ar¹⁴⁺ and Be-like Ca¹⁶⁺ have been performed by using distorted-wave collision package AUTOSTRUCTURE.^[33] For the Li-like Ar¹⁵⁺ and F-like Ni¹⁹⁺ the FAC^[34] was used to calculate DR resonance cross sections. It should be noted that the difference between these two codes are described in Ref. [35] The integrated DR cross section for state d can be written as

Figure 2 shows the absolute recombination rate coefficient for Be-like Ar¹⁴⁺, Li-like Ar¹⁵⁺, Be-like Ca¹⁶⁺, and F-like Ni¹⁹⁺ ions as functions of electron–ion collision energies. The electron–ion recombination spectra include RR and DR and cover the energy range of 0 meV–1000 meV in the center of mass energy frame. In Fig. 2(a), the total experimental recombination rate coefficient is represented by connected black solid circles, dashed violet lines denote theoretical RR rate coefficient. The green solid lines denote the sum of calculated RR and DR rate coefficients, which was obtained from the convolution of calculated RR and DR cross section with the anisotropic electron velocity distribution. However, a very large discrepancy can be found between the experimental results and the theoretical calculations, because the theoretical results of DR rate coefficients have very large uncertainties for multi-electron ions in low energy range. For accurate determination of the electron beam temperature in each experiment, we fitted each spectrum with several DR resonance line profile. In the fit for each line profile the corresponding cross sections were convoluted with the same function as shown in Eq. (5), which can be rewrite as

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. The absolute recombination rate coefficient for Be-like Ar14+, Li-like Ar15+, Be-like Ca16+, and F-like Ni19+ respectively. (a) Comparison of the experimental result to the theoretical calculations, the experimental data represented by connected black solid circles, the violet dashed line is for RR rate coefficient and the green line is from theoretical data of RR + DR. (b) Comparison of the experimental results with fitted data by taking into account of RR + DR resonances. Blue solid line corresponds to the fitting of DR. The red solid line indicates the fitted data including RR + DR, and Δ α is the enhancement of the experimental rate coefficient over the fitted rate coefficient α0. The transverse and longitudinal temperature obtained from this fitting are kBT∥ = 2.40(6) meV and kBT⊥ = 11.91(87) meV for Ar14+ and kBT∥ = 0.8 meV, kBT⊥ = 40 meV for Ar15+ and Ca16+, and kB T∥ = 0.56(7) meV and kBT⊥ = 23(1) meV for Ni19+.

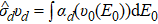
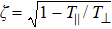
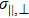
Therefore, from the fitting of the line profile given by Eq. (11) to the measured resonance profile, the transverse and longitudinal temperatures of the electron beam can be obtained,^[31] as shown in Fig. 2(b). The solid red line is the fitted results including RR + DR. It should be noted that the first resonance peak was treated as a Lorentzian line shape multiplied by a factor of E_res/E in each fitting.^[18] The obtained transverse and longitudinal temperatures of electron beam were k_BT_∥ = 0.56(7) meV and k_BT_⊥ = 23(1) meV for the Ni¹⁹⁺, k_BT_|| = 2.40(6) meV and k_BT_⊥ = 11.91(87) meV for Ar¹⁴⁺, k_BT_|| = 0.8 meV and k_BT_⊥ = 40 meV for Ar¹⁵⁺ and Ca¹⁶⁺, respectively. It can be found that the experimental RR rate coefficient exceeds the fitting and theoretical results a₀ at low electron–ion collision energy below 10 meV as shown in Fig. 2(b). This effect is known as the RR rate coefficient enhancement, which can be written as Δα, where Δα = α_Experiment − α₀ is the difference between experimental result α_Experiment and fitting result α₀. The RR enhancement factor can be defined as ε − 1 = Δα/α₀. At energies below 4 meV, the experimental rate coefficient shows an enhancement (Δα) over a fitted rate coefficient (α₀) by a factor of about 3.9 for Ar¹⁵⁺, 1.9 for Ar¹⁴⁺, 1.5 for Ca¹⁶⁺, and 2.1 for Ni¹⁹⁺, respectively.

From the theoretical model described in,^[38] the relationship between the recombination rate coefficient enhancement Δα^RR to the main physical parameters concerning to electron–ion recombination experiments can be written as

Fig. 3.

Figure Option ViewDownloadNew Window

Fig. 3. (a) The dependence of the RR rate coefficient enhancement Δα of bare-ions on charge state of ions. The violet empty triangles represents experimental data of the CRYRING[8,9] and the blue color empty square is the TSR data.[5] The error bars represent the contribution from the uncertainty of the excess rate, in this plot 20% uncertainty has been assumed for all the data. The solid line is the q2.8 scaling for the bare ions. (b) The dependence of the RR rate coefficient enhancement Δα of non-bare ions on the charge state q of the ions. The empty green circles represent experimental RR rate enhancement data of the CSRm for non-bare ions. The 30% experimental uncertainty has been taken and the solid red line is the q3.0 scaling.

In Fig. 3(a), the RR enhancement factors from CRYRING^[9] and TSR are shown^[5] for the bare ions. Experimental uncertainty of 20% was estimated for all the bare ions data. The red solid line is the q^2.8 scaling, which is in agreement with the scaling behavior found at the CRYRING by Gao et al. (1997).^[9] Figure 3(b) shows the excess RR rate coefficient Δα^RR for non-bare ions plotted as a function of nuclear charge state of the ions q by using scaling law. The empty green circles represent the present CSRm data for non-bare ions with 30% experimental uncertainty. The scaling of q^3.0 has been found for the excess rates for non-bare ions CSRm data as represented with the solid red line. It should be noted that the scaling law fitted very well to the bare ions data compared with non-bare ions.

In Fig. 3(b) the data for Li-like Ar¹⁵⁺ is away from the fitted line significantly. It might be due to the strong contribution from low laying DR resonances to the RR rate coefficient. These low laying DR resonances overlap with the RR rate coefficient near to threshold which results in the rate enhancement. For all other non-bare ions, the fitting is satisfactory which shows the validity of the scaling law for recombination experiments for both bare and non-bare ions at the storage rings. These findings indicate that the low-energy DR resonances will overlap with the RR rate enhancement at very low electron–ion collision. One has to be careful when comparing the results from different facilities since the experimental conditions vary drastically. The influence from other parameters such as the transverse temperature kT_⊥, longitudinal temperature kT_∥, and magnetic field B has to be considered. Also one has to take into account of this RR rate enhancement and carefully subtract it from DR spectra during the investigation of the atomic structure by DR method. In addition, to the atomic structure studies, we also use this atomic data for x-ray astrophysical implications, the atomic databases such as AtomDB version 2.0 and XSPEC are used for modeling astrophysical plasmas. For these atomic databases one needs to transform the DR rate coefficients to the plasma rate coefficient, by convoluting it with average Maxwellian distribution. Since, from this work we conclude that the RR rate enhancement is concerning to the storage ring merged beams recombination method and we do not expect the RR enhancement effect in astrophysical environment. Therefore, one should subtract very carefully the RR enhancement from DR rate coefficient before transforming it to plasma rate coefficient. If the RR enhancement effect is not carefully subtracted from the DR spectra then the overlap between RR rate enhancement and DR resonances close to the threshold will be translated into plasma rate coefficient after convolution, which will create large uncertainties in theoretical and experimental data at the low energy range.

In this work, a series of measurement of the absolute recombination rate coefficients of Be-like Ar¹⁴⁺, Li-like Ar¹⁵⁺, Be-like Ca¹⁶⁺, and F-like Ni¹⁹⁺ have been performed at the storage ring CSRm at Institute of Modern Physics, Lanzhou, China. Data analysis is focused on the electron–ion collision energy range from 0 meV to1000 meV. The experimental electron–ion recombination spectra have been fitted with flattened Maxwellian function which include the contributions from RR and DR processes. The theoretical results for RR rate coefficients were calculated by using modified semi-classical formula given by Bethe and Salpeter (1957). The contribution from DR rate coefficients to the recombination spectra were calculated by employing AUTOSTRUCTUTRE and FAC codes. A strong enhancement of the measured RR rate coefficient over the fitted and calculated rate coefficients have been observed in all recombination spectra for the collision energies below 10 meV.

The present evaluation of the nuclear charge dependence of the RR rate enhancement Δα results in ∼ Z^3.0 scaling for non-bare ions. We have also compared our results with the RR enhancement factors from other storage rings for bare ions. Our recent findings indicate that the RR rate enhancement is a general phenomenon found in all storage ring measurements for both bare and non-bare ions. A smooth dependence of RR rate coefficient enhancement on nuclear charge states has been found for bare-ions. For the non-bare ions the RR rate enhancement dependence on nuclear charge is not smooth, which indicates that the enhancement is partly coming from the low-n DR resonances located close to the threshold. In addition, we have also pointed out that the RR enhancement rate strongly influences the DR resonances at very low relative energies which will also be translated to the plasma rate coefficient used for astrophysical implications.