† Corresponding author. E-mail:
We consider a modified Noguchi network and study the impact of the nonlinear quadratic dispersion on the dynamics of modulated waves. In the semi-discrete limit, we show that the dynamics of these waves are governed by a nonlinear cubic Schrödinger equation. From the graphical analysis of the coefficients of this equation, it appears that the nonlinear quadratic dispersion counterbalances the effects of the linear dispersion in the frequency domain. Moreover, we establish that this nonlinear quadratic dispersion provokes the disappearance of some regions of modulational instability in the dispersion curve compared to the results earlier obtained by Pelap et al. (Phys. Rev. E
During the last decades, the transmission electrical lines are increasingly used to study the behavior of the nonlinear dispersive media. Indeed, since the pioneering work of Hirota and Zuzuki[1] on electrical lines simulating the propagation of solitons in the atomic lattice of Toba,[2] the nonlinear transmission lines (NLTLs) have created passion and debate. Therefore, several models have been proposed in order to explain various physical phenomena in different branches of science. Indeed, Nejoh proposed a new type of nonlinear transmission line to describe the density depression and the collisionless shock wave in plasmas.[3] Twenty years later, Enjieu et al. modeled the nonlinear dynamics of plasma by using an anharmonic oscillator.[4] In the same spirit, Ainamon et al. studied the nonlinear dynamics of polarization oscillations of certain materials when they are subjected to the action of an electromagnetic wave modeled by the multi-frequency forced Duffing equation.[5] More recently, Makenne et al. exploited electrical lines to simulate periodic and chaotic motions of plants under the action of the wind.[6] Ndzana et al. also studied the dynamics of ionic waves in a microtubule modeled by a nonlinear resistor, inductor, and capacitor transmission line.[7] These few investigations partially justify the interest given to the electrical transmission lines since the first line of Hirota and Suzuki.
On the other hand, Noguchi built a new type of electrical transmission line to study experimentally the propagation of the first-order KdV solitons.[8] This network was also exploited to examine experimentally the properties of the second-order KdV solitons by using a new potential that generalized the Toda potential.[9] Based on the modified Noguchi line with linear dispersion, Pelap and Faye established a generalized criterion for the Benjamin–Feir instability and determined the exact solutions of the wave equation that governed the dynamics of the network.[10] Ndzana et al. considered a discrete dissipative Noguchi network for investigating the modulational instability (MI) phenomenon as well as the chaotic behavior of this dispersive medium.[11] Recently, the dynamics of elliptical waves in the same line was checked by other authors.[12] While examining the Noguchi network with nonlinear dispersion, Yamgoue et al. proposed exact solitary wave solutions of a nonlinear Schrodinger equation model with saturable-like nonlinearities.[13] More recently, Deffo et al. introduced a new model of two-dimensional Noguchi nonlinear electrical network and showed that the dynamics of small amplitude signals are described by a (2 + 1)-dimensional Zakharov–Kuznetsov equation type.[14] Several other variants of Noguchi nonlinear electrical transmission lines have also been proposed in the literature.[15,16]
The models studied above have led to very interesting and encouraging results. However, these models largely consider a linear dispersion in NLTLs, which limits the applicability of the established results to only a few physical phenomena. For example, the NLTLs with linear dispersion give a good description of the dynamics of the classical soliton while they fail to describe the compact soliton.[17] Likewise, several interesting phenomena in NLTLs cannot be produced by the linear dispersion alone.[18] In addition, the few studies reported on NLTLs with nonlinear dispersion overlook the effects of this nonlinearity.[13,17]
In this work, we consider a modified Noguchi electrical transmission line with a nonlinear quadratic dispersion and examine the new features of this factor on the dynamics of modulated waves traveling in the network. This paper is organized as follows. In Section
The physical model considered within this paper consists of many identical LC blocks connected as illustrated in Fig.

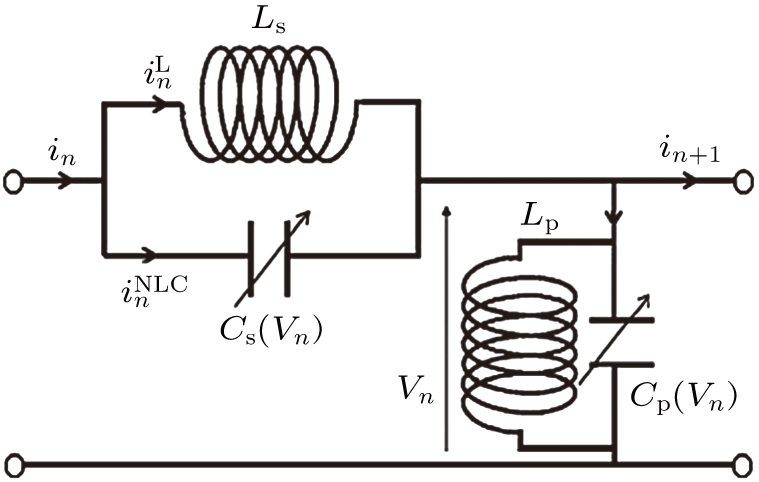 | Fig. 1. Schematic representation of a unit cell. The dispersive nonlinear electrical transmission line is made of n identical units. |
By applying the Kirchhoff's law to the circuit of Fig.
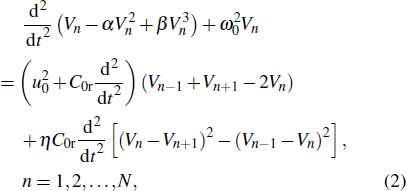
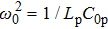

In the linear domain of Vn, i.e., neglecting the terms of power greater than 1, and assuming a sinusoidal wave in which Vn is proportional to exp(i (kn − ωt)), we get a linear dispersion relation of the following form:


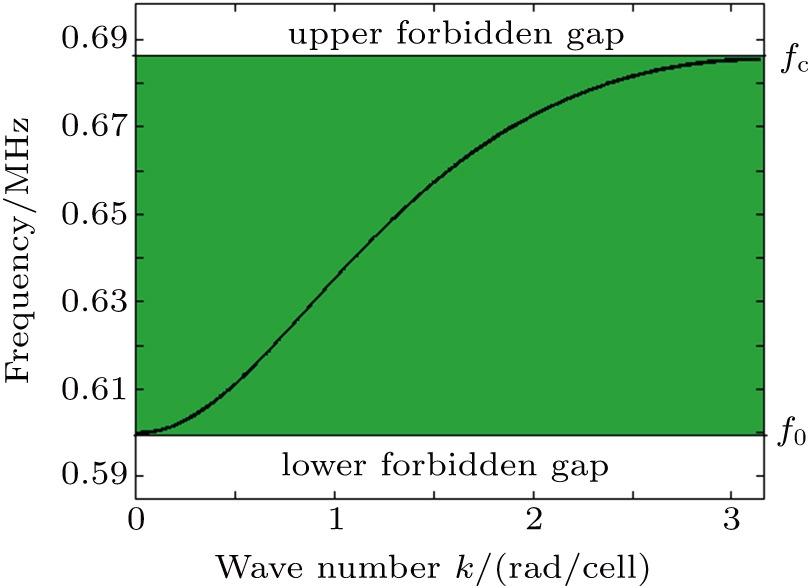 | Fig. 2. The linear dispersion curve of the network with wave vector k (rad/cell) for C0r = 0.3, u0 = 2.5786 × 106 rad/s, and ω0 = 3.7689 × 106 rad/s. |
The corresponding linear group velocity associated to the wave packet is defined below

In this subsection, our attention is focused on the derivation of the cubic nonlinear Schrödinger equation describing the propagation of the modulated waves in the network. During this derivation, we assume that the envelope of the wave varies in time and space with regard to a given carrier wave with angular frequency ω and wave number k. To achieve this end, we call the reductive perturbation method in the semi-discrete limit to expand the voltage in the general form[19]


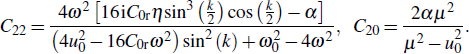

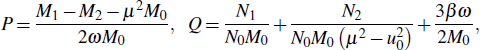
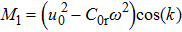
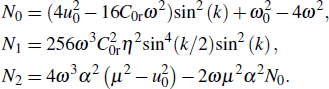
Modulational instability (MI) is a phenomenon that results from the interplay between nonlinearity and either the dispersion in the time domain or the diffraction in the spatial domain. It has been studied in various fields of science, namely, nonlinear optics,[21] condensed matter physics,[22] plasma physics,[23] and biophysics,[24] just to name a few. These investigations indicate that the MI phenomenon is an underlying physical mechanism which has several advantages. For instance, it is indispensable for understanding the relevant dynamic processes in the Bose–Einstein condensates systems which include domain formation, generation and propagation of soliton waves.[25] Similarly, MI is an indicator of the presence of discrete solitons in discrete dissipative systems and can be exploited to generate a soliton train at high repetition rate.[26] In inhomogeneous nonlinear systems, MI may be considered as the leading mechanism for energy localization as well as the formation of traveling intrinsic localized modes.[27]
In the NLS models, this phenomenon occurs if the product PQ is positive. In fact, the nonlinear dispersion relation is given by


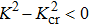

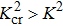
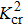
To clearly establish the effect of the nonlinear quadratic dispersion parameter η on the dynamics of waves in the network, we check the evolution of the coefficients of Eq. (
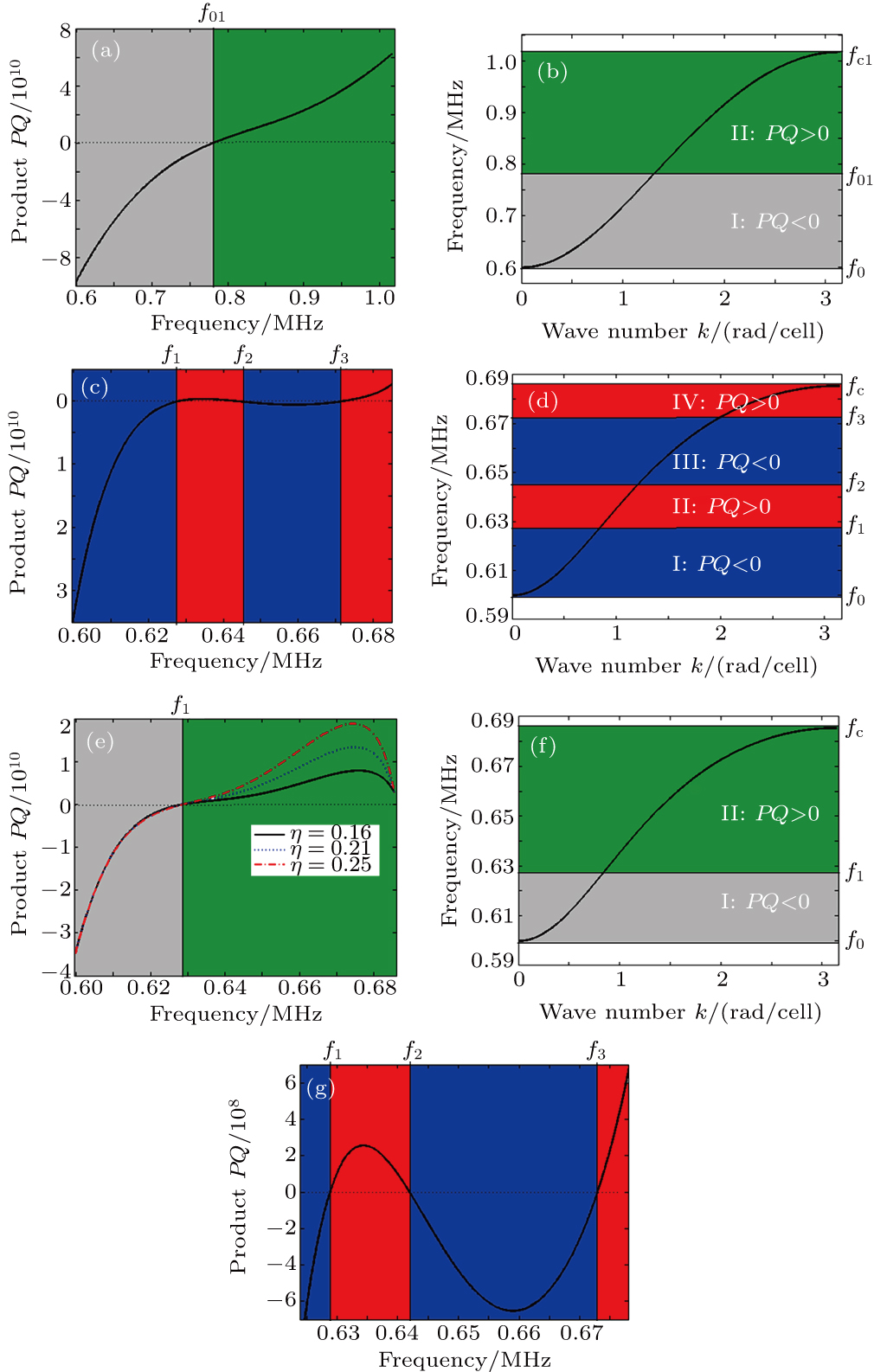
Figure
Figure
First, we start with the case C0s = 0 and η = 0 dealing with the absence of the capacitor in the series branch of Fig.
Here, there exist two domains in which the product PQ can be positive or negative (Figs. f ∈ [f0, f01], PQ < 0, the wave plane remains stable under modulation and the solutions of the NLS equation are dark solitons; f ∈ [f01, fc1], PQ > 0, the wave plane is unstable under modulation and the solutions of the NLS equation are envelope solitons.
Next, we consider the case where the capacitor in the series branch of Fig. f ∈ [f0, f1], PQ < 0, the wave plane is modulationally stable and the solutions of Eq. ( f ∈ [f1, f2], PQ > 0, the wave plane is modulationally unstable and equation ( f ∈ [f2, f3], PQ < 0, the wave plane remains stable under modulation and the solutions of Eq. ( f ∈ [f3, fc], PQ > 0, the wave plane is unstable under modulation and the solutions of Eq. (
Finally, when the capacitor in the series branch of Fig. f ∈ [f0, f1], PQ < 0, the wave plane remains modulationally stable and equation ( f ∈ [f1, fc], PQ > 0, the wave plane is unstable under modulation and the NLS equation admits envelope solitons solutions.
From the above-mentioned cases, it is clear that the nature of the capacitor in the series branch of Fig.
We intend to perform numerical simulations on the exact discrete Eq. (
We start by reminding that a plane wave introduced in the line becomes unstable in the focusing media (PQ > 0) and remains stable in the defocusing media (PQ < 0). To numerically check it, the following signal is applied at the input of the line:
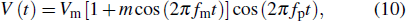
As a first example of the outcome of these experiments, figure
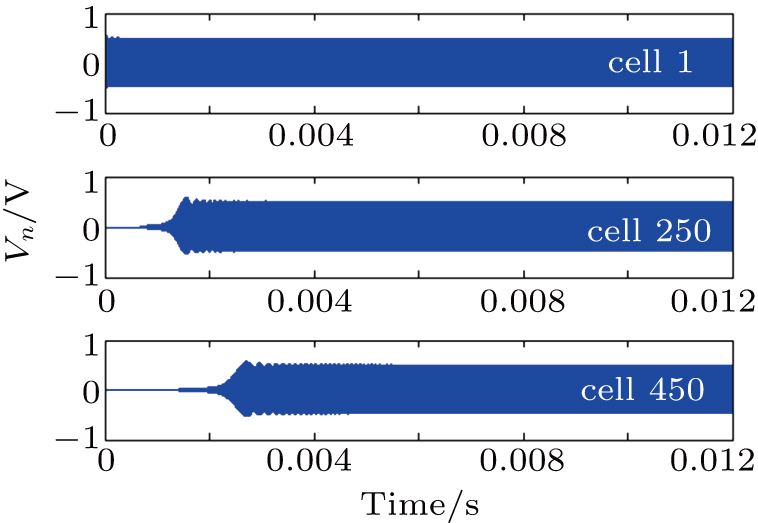 | Fig. 6. Modulational stability behavior of the plane wave with the frequency fp = 667.30 kHz in the network that belongs to domain III of the dispersion curve (Fig. |
For further illustrations, the same carrier frequency fp = 667.30 kHz of the plane is chosen but in domain II of Fig.
To experience the transmission of the envelope soliton through our model for several bands of frequencies dictated by Fig.
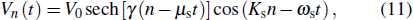
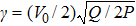
In order to avoid signal reflection that disturbs the accurate observation of the wave propagation in the network, the voltage across the other extremity is set to zero and the experiment is run for a sufficiently long time. Results of the numerical simulations are given in Figs.
In the first case (Fig.
On the other hand, figure
We have studied analytically and numerically the effects of the nonlinear quadratic dispersion on the dynamics of modulated waves in a modified Noguchi transmission line. We have demonstrated through the reductive perturbation approach that the propagation of modulated waves in the network is described by the nonlinear cubic Schrödinger equation. The analytic expressions of its various coefficients were established and their analyses revealed that the nonlinear quadratic dispersion has profoundly modified the dynamics of the system, results which contrast with the case of linear dispersion previously obtained. For instance, our investigations have shown that this nonlinear quadratic component counterbalances the effects of the linear component. Moreover, we have found that the quadratic nonlinear dispersion reduces the MI domains to two regions, unlike four in Ref. [12] and allows the possible propagation of bright and dark solitary signals at the same frequency through the network. Numerical simulations performed in the framework of the nonlinear lattice equation have led to outcomes that are in perfect agreement with the analytical predictions. In addition, our study can be useful to make a better choice of the quadratic parameter and to help a better understanding of the results of experiments of the propagating modulated wave in the transmission lines with nonlinear dispersion.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] |