† Corresponding author. E-mail:
We deal with the Wick-type stochastic fractional Korteweg de–Vries (KdV) equation with conformable derivatives. With the aid of the Exp-function method, white noise theory, and Hermite transform, we produce a novel set of exact soliton and periodic wave solutions to the fractional KdV equation with conformable derivatives. With the help of inverse Hermite transform, we get stochastic soliton and periodic wave solutions of the Wick-type stochastic fractional KdV equation with conformable derivatives. Eventually, by an application example, we show how the stochastic solutions can be given as Brownian motion functional solutions.
The nonlinear fractional differential equations (FDEs) are constructed by mathematical modeling of some complex physical phenomena. The study of such nonlinear physical models through wave solutions analysis corresponding to their FDEs has a dynamic role in applied sciences. The Korteweg–de Vries (KdV) equations have been applied to a broad variety of material science phenomena as a model for the development and communication of nonlinear waves. The KdV equation was introduced to describe shallow water waves of long wavelength with small amplitude. The soliton and periodic exact solutions of the KdV equation may be of significance in many physical contexts as collision-free hydromagnetic waves, stratified internal waves, particle acoustic waves, plasma physics, and so on.[30,38,42]
This work is devoted to investigate the stochastic fractional KdV equation with conformable derivatives
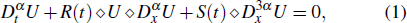
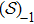
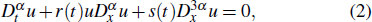
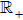
There are many studies done for the definition and properties of the conformable derivative. Conformable forms of the chain rule, Gronwalls inequality, exponential functions, Taylor power series expansions, integration by parts, and Laplace transform have been presented by Abdeljawad in Ref. [1]. Benkhettoua et al.[3] have presented the calculus of the conformable time-scale. The heat equation with conformable derivatives was investigated by Hammad and Khalil in Ref. [18]. Chung[8] used the conformable derivative and integral to study the fractional Newtonian mechanics. Moreover, the deterministic conformable partial differential equations (PDEs) became an important subject in mathematical physics. So, many scholars paid more attention to their approximate and analytical solutions. The existence and uniqueness theorems for the linear sequential differential equations with conformable derivatives were proved by Gokdogan et al. in Ref. [17]. Eslami and Rezazadeh[9] gave a set of analytical solutions to the Wu–Zhang system with conformable derivative via the first integral method. The stochastic traveling wave solutions for the fractional coupled KdV and two-dimensional (2D) KdV equations were obtained by the modified fractional sub-equation method in Refs. [13,15], respectively.
Many researchers have studied the subject of random traveling wave, which is a significant subject of stochastic partial differential equations (SPDEs). Wadati[37] first proposed and discussed the stochastic KdV equation and discussed the propagation of soliton of the KdV equation under the effect of Gaussian noise. Furthermore, Ghany and Hyder,[12,13,15,16] Chen and Xie,[5–7] Hyder and Zakarya,[26,27] and Hyder[24,25] investigated a wide class of Wick-type stochastic evolution equations by using different extension methods and white noise analysis. Recently, many research works have done to investigate the conformable PDEs and their exact solutions via various methods. In Ref. [46], a conformable sub-equation method was proposed to construct exact solutions of the space–time resonant nonlinear Schröinger equation. By using the generalized exponential rational function method, new periodic and hyperbolic soliton solutions were constructed to the conformable Ginzburg–Landau equation with the Kerr law nonlinearity.[10] Also, a family of exact solutions were obtained for the space–time conformable generalized Hirota–Satsuma-coupled KdV equation and coupled mKdV equation using the Atangana’s conformable derivative and conformable sub-equation method.[43] The analysis of the first integral method was given in Refs. [44,45] to construct exact solutions of the nonlinear PDEs described by beta-derivative. Moreover, new optical, dark, complex, and singular soliton solutions were obtained for some nonlinear PDEs with M-derivative.[2,11] The investigation of exact and approximate solutions of nonlinear evolution equations plays an important role in the study of nonlinear physical phenomena. Many helpful methods such as bilinear transformation method,[35] the modified Clarkson and Kruskal (CK) direct method,[39] the multi-scale expansion method,[33] the binary Bell polynomials method,[48] the Riemann–Hilbert method,[41] and the approximate symmetry method[28] have been presented in the recent literature. He and Wu[19] introduced a concise and straightforward method, called the Exp-function method, to obtain generalized soliton, periodic, and compacton-like solutions for many nonlinear PDEs.[21, 49] In this method, the exact solutions are obtained in the form of an exponential type rational function in which both the numerator and denominator are polynomials of exponential functions. The main merit of the Exp-function method over the others lies in the fact that a great variety of exact solutions to nonlinear PDEs can be derived easily by choosing the parameters that appear, and the degrees of the polynomials that are present, in the solution. The main feature of the exact solutions obtained by the Exp-function method is their reducibility.[32] Also, the proposed Exp-function method leads to both the generalized solitonary solutions and periodic solutions. Moreover, the solution procedure, by the help of Mathematica, is of utter simplicity, and can be easily extended to all kinds of nonlinear equations.
Our aim in this work is to obtain new stochastic soliton and periodic wave solutions for the variable coefficients fractional KdV equation and Wick-type stochastic fractional KdV equation with conformable derivatives. Using white noise theory and Hermite transform, the Wick-type stochastic fractional KdV equation with conformable derivatives can be transformed to a deterministic fractional KdV equation containing conformable derivatives. In view of the proposed Exp-function method, the exact solutions of the deterministic fractional KdV equation are constructed in the form of an exponential type rational function in which both the numerator and denominator are polynomials of exponential functions. The highest and lowest degrees of the polynomial sums in both the numerator and denominator are determined through a homogeneous balance between the highest nonlinear term and the linear term of the highest order derivative appearing in the deterministic fractional KdV equation. Using some symbolic computation and the software Mathematica, we can find soliton and periodic wave solutions for the variable coefficients fractional KdV equation with conformable derivatives. Under pronounced conditions, we can apply the inverse Hermite transform to obtain stochastic soliton and periodic wave solutions for the Wick-type stochastic fractional KdV equation with conformable derivatives. Finally, by an application example, we show how the stochastic solutions can be given as Brownian motion functional solutions. This paper is organized as follows. In Section
In this subsection, we recall the definitions and some properties of the conformable derivative and integral.

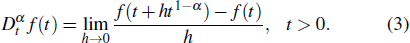
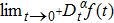


The following theorems give some sustainable properties for the conformable derivative.
where ′ denotes the usual derivative with respect to t.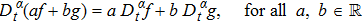





The Gaussian white noise analysis starts with the rigging 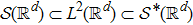


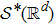
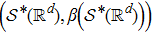

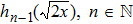
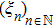


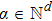


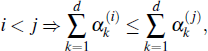
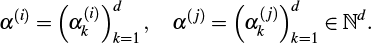
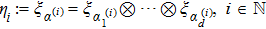
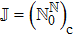
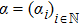
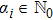


Let 


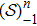
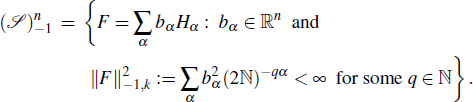
The family of seminorms ||f||1,k, 



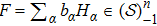
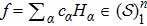

The Wick product of two distributions 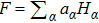
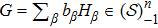
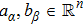

Let 


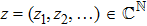
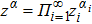
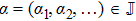
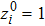
For 
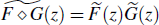
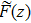

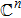
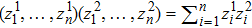

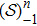

In what follows, the stochastic distribution process (or 







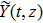
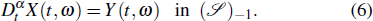

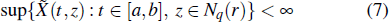
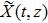

Now, consider a conformable nonlinear PDE in the form


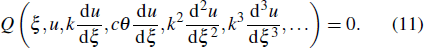
Applying Hermite transform to Eq. (
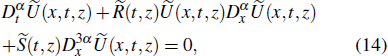
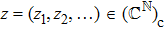
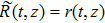
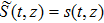
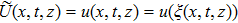
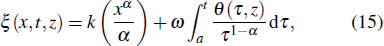
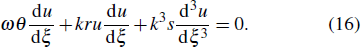
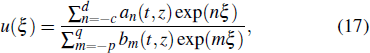

Now, for some special cases of the numbers p,c,d, and q, we can express the general solution of Eq. (
Assume that k is an imaginary number, the above soliton wave solutions can be transformed to periodic solutions[19,20] according to the transformations

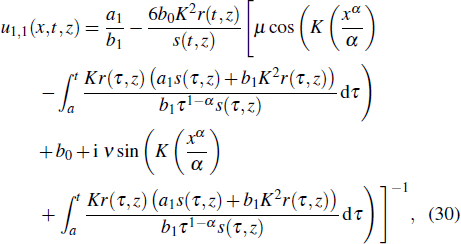
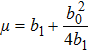
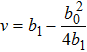

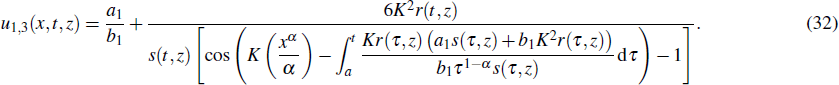
Following the same technique as presented for the solution (
The properties of the exponential and trigonometric functions yield that there exists a bounded open set 



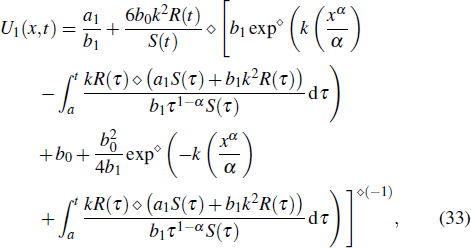





In this section, we provide specific application example and numerical simulation to demonstrate the effectiveness of our results and to justify the real contribution of these results. We observe that the solutions of Eq. (
Assume that α = 1, R(t) = ρS(t), and S(t) = f(t) + σ Wt, where ρ and σ are arbitrary constants, f(t) is a bounded measurable function on 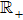


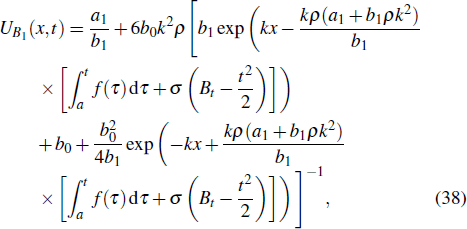
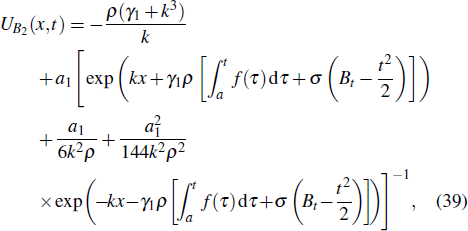



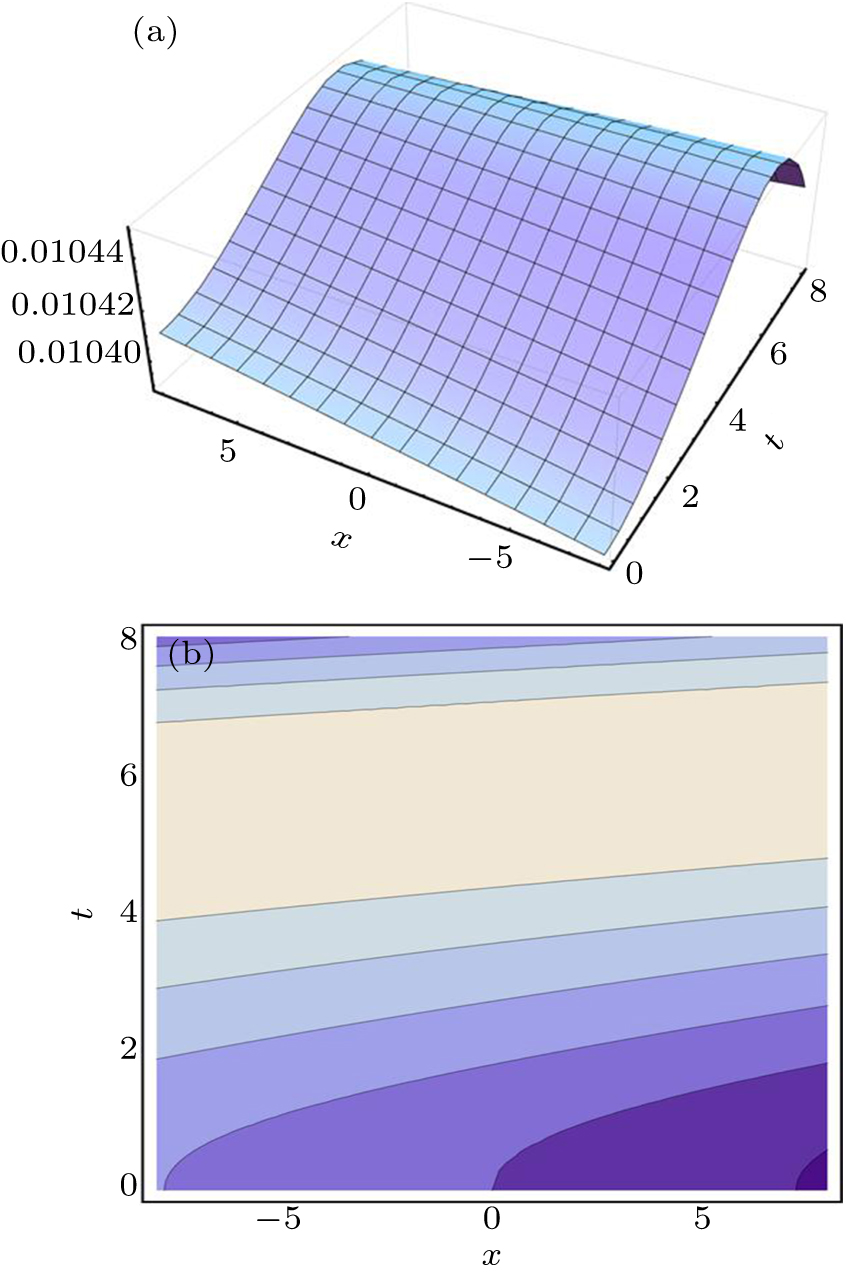
The numerical simulation of the solution
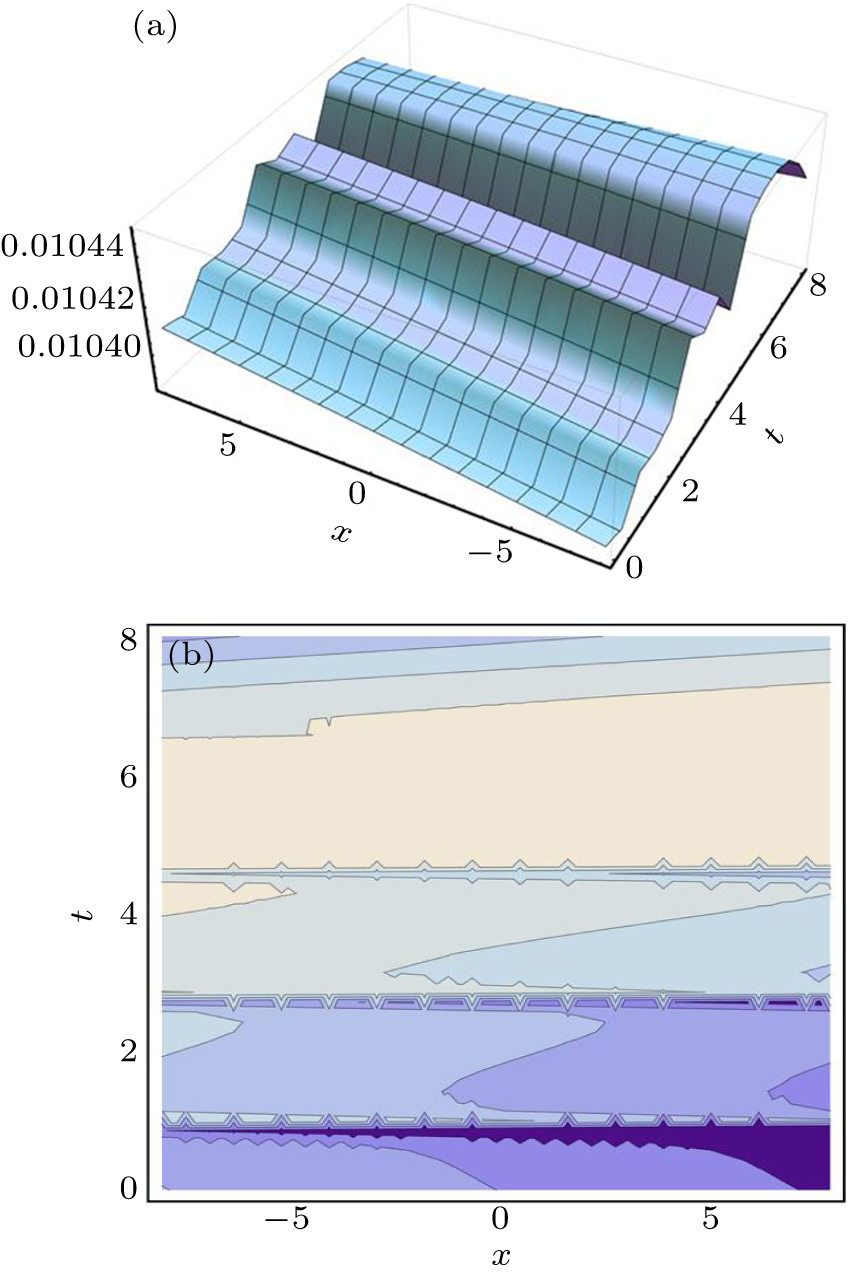 | Fig. 1. (a) The 3D plot of the solution ( |
Due to the fact that the stochastic models are more realistic than the deterministic models, we concentrate our study in this paper on the Wick-type stochastic fractional KdV equation with conformable derivatives. Besides that, we investigate and solve the deterministic fractional KdV equation with conformable derivatives. By using the Exp-function method, Hermite transform, and white noise theory, we produce a new set of exact soliton and periodic wave solutions for the variable coefficients and fractional KdV equation with conformable derivatives. With the aid of inverse Hermite transform, we obtain stochastic soliton and periodic wave solutions for the Wick-type stochastic fractional KdV equation with conformable derivatives. Furthermore, we show by an example how the stochastic solutions can be given as Brownian motion functional solutions. Moreover, if α = 1, then the stochastic solutions (
Moreover, our exact solutions can be compared with other exact solutions which are obtained by different methods. For example, if we set α = b1 = 1, a1 = σ0, b0 = 2, k = 2δ, a = 0, R(t) = r(t), S(t) = s(t), and 


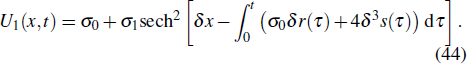
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] |