† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 51705459) and the China Postdoctoral Science Foundation.
The key to high manoeuvre ability in bird flight lies in the combined morphing of wings and tail. The perching of a wild Haliaeetus Albicilla without running or wing flapping is recorded and investigated using a high-speed digital video. A shape reconstruction method is proposed to describe wing contours and tail contours during perching. The avian airfoil geometries of the Aquila Chrysaetos are extracted from noncontact surface measurements using a ROMBER 3D laser scanner. The wing planform, chord distribution and twist distribution are fitted in convenient analytical expressions to obtain a 3D wing geometry. A three-jointed arm model is proposed to associate with the 3D wing geometry, while a one-joint arm model is proposed to describe the kinematics of tail. Therefore, a 3D bird model is established. The perching sequences of the wild eagle are recaptured and regenerated with the proposed 3D bird model. A quasi-steady aerodynamic model is applied in the aerodynamic predictions, a four-step Adams–Bashforth method is used to calculate the ordinary differential equations, thus a BFGS based optimization method is established to predict the perching motions.
A flying animal flaps its wings to generate both thrusts and lifts to balance the drag and weight. After thousands of years of evolution, the wing of flying animals moves generally with complex patterns in both wing kinematics and deformations,[1] and a bird can colonize almost all terrestrial habitats on earth, such as cliff, distant islands. Different flying animals have different flight features, resulting in various aerodynamic mechanisms. For example, a fruit fly beats its wings with a very high frequency (about 100 Hz) to generate lift as higher as possible. The main feature is the strong unsteady flow with a low Reynolds number which restricts its thrust generations and high lifts.[2–4] Unlike the insect, a bat usually flies at a speed of 3–5 m/s, and the flapping frequency is about 10 Hz during a moderate flight.[5] On the other hand, characteristic speed of a pigeon is about 15 m/s, with wing flapping at a frequency of 1–2 Hz. The generated lift coefficient is about 0.47 and quasi-steady aerodynamics can be used to predict the lifts and drags.
A detailed learning of avian locomotion is an essential step in revealing the excellent flight abilities of bird flight.[6] Unique flight form of wingbeats once intrigued scientists, recording the form of wingbeats has been a long issue.[7,8] Measurements of bird flight were raise by Brownd over 60 years ago, and then some theoretical models were proposed to analyze aerodynamic mechanisms of bird flight.[9–13] An inverse computational method originated from modelling terrestrial locomotion, which gives an opportunity to simulate wingbeats without inputting measured kinematic data.[14,15] Recently, Parslew and Crowther proposed and validated a robust theoretical model for predicting the form of avian wingbeats using the inverse computational method.[16] The avian wing geometry of large bird, such as seagull, merganser, teal and owl have also been investigated.[17,18] Geometry shapes of a bird wing, including airfoils, can be quantified using analytical expressions, and a jointed arm model was also developed to represent the avian wing kinematics recovered from videos. The primary feather has important effects on the aerodynamics, the cutting of primary feathers at the tip will reduce the distance flown dramatically.[19] Recently, we proposed a modified 3D model of barbs to describe separating and recovering processes of neighboring barbs, the critical connecting force between barbs were quantified by an experimental approach.[20] The airfoil in the position of 40% spanwise of the long-eared owl wing has excellent aerodynamic performance and low noise characteristics. It is studied and extracted to reconstruct the bionic blades with improved aerodynamic performances by Qu and Liu.[21] It is impressive that the perching of steppe eagle Haliaeetus Albicilla was studied.[22] The aeroelastic deflections of the covert feathers of an eagle were investigated using onboard and high-speed digital video during wide-ranging free flight. Also, high-resolution and high-speed digital videos were used to study indoor and outdoor perching manoeuvres.[23,34] It has been raised that rapid pitch-up plays an important role in high manoeuvrability of a large prey which enables the bird to speed down, change direction or climb in a short time. During the rapid pitch-up, kinetic energy was changed to potential energy. Lift can be enlarged incredibly under a large angle of attack of the up stroking, which will drive a bird upward. As the deep stall, the drag can be enlarged to induce the loss of the total kinetic energy to the wake.[25] Both the high lift and the high drag offer the opportunity to change the flight attitude quickly.
After investigations of hundreds of flying videos of large birds of prey, such as gliding, hovering, perching, and fighting, it is the combined morphing of wing and tail that allow an eagle change its flight attitude in the shortest time (flapping is unnecessary). Also, rapid transition between a steady glide and a deep stall often appears.[23] During those maneuvering flights, perching with zero running distance is one of the most simple but basic flight patterns. An eagle was observed to land on the ground without running or wing flapping but with combined morphing of wing and tail to achieve a “soft landing”. The corresponding perching sequences were investigated. A bird skin construction method was also proposed to describe motions of both wing and tail, the perching sequences of the eagle was also numerically reproduced.
Aquila Chrysaetos is a large bird of prey, and it has quite excellent flying abilities, which help it perching and fighting, etc. However, the Aquila Chrysaetos is a first-class national protected animal of China, any sale, purchase or use of the wild animal or its products is forbidden.
The scanning object is a specimen of Aquila Chrysaetos at Zhejiang Museum of Natural History as shown in Fig.
We used a ROMBER absolute arm with integrated scanner to which a three-dimensional non-contact laser scanner is attached for the bird surface measurements. The ROMBER absolute arm is a hand-held mechanical device with high accuracy. Before the experiment, the ROMBER arm was fixed to the ground using glue to ensure that the tower of the ROMBER will keep unmoved. On the ROMBER arm, the position of the scanner relative to a given coordinate system is known accurately. An integrated laser scanner is designed to capture 3D point data across a range of surface types. With an ultra-wide laser stripe of up to 150 mm, the scanner can capture 7520000 points per second. The accuracy of the complete scanning system is verifiable and traceable, the accuracy of surface data is within 0.01 mm. Operating with the Geomagic Wrap software, the system works based on the principle of laser stripe triangulation. A laser line was project onto the object and the line was viewed by cameras so that distance variations on the object can be seen. The resulting scanning data will be a profile that contains the shape information. The scanner can work for a variety of materials and colors including black and white which are common for the feathers of Aquila Chrysaetos. The Geomagic Wrap software can output data in a CATIA format, which be dealt using the data cloud method.
Figure
The scanned tail point cloud is shown in Fig.
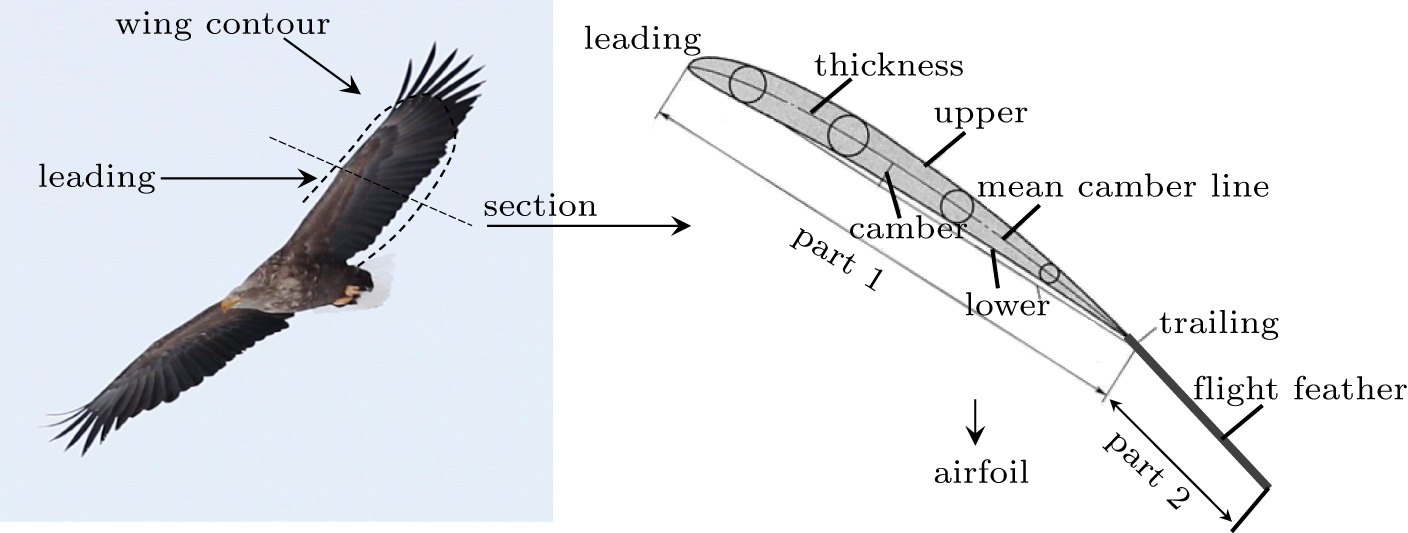
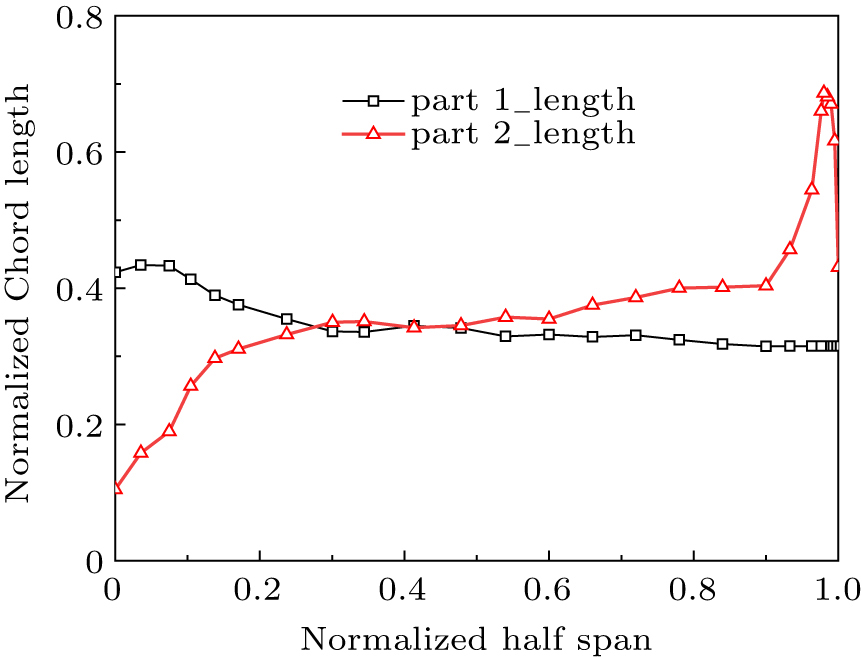
The wing is covered with covert feathers and flight feathers, the coverts provide most of the lower surface contour and all the upper surface contour over the thick forward sections. The under-wing and upper-wing once were anatomical identified as seven regions.[26] To the simplify the wing shapes, the sectional airfoil cut through a primary feather is decomposed into two parts. They are named as part 1 and part 2, which are a typical wing airfoil (without primary feather) and a primary feather respectively, as shown in Fig.
As part 1, the camber line and the thickness distribution were quantified first, thus the upper surface was expressed as an addition of the camber line and thickness distribution, the lower surface was expressed as a subtraction of the camber line and thickness distribution,
 |
 |
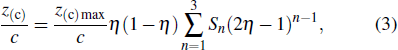 |
 |
As part 2, a local coordinate was arranged at the feather root, an exponential function was used to describe the bending of the secondary feather along the x axis,
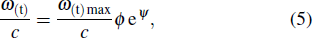 |
Since the particular length of part 1 and part 2 of each feather can be obtained, the chord distributions along the span were obtained by measuring the 26 airfoils. The wing planform was also measured by locating leading points and trailing points along the span. Each tail feather is assumed to have the same length distribution and width distribution, which was assembled to be a cylindroid body. Thus, a fan-shape tail was expected for the eagle and no thickness of tail feather was considered in the current research.[28]
The bird wing skeleton consists of the humerus which is attached to the muscles in the breast, ulna, radius, carpometacarpus and phalanges,[29] as shown in Fig.
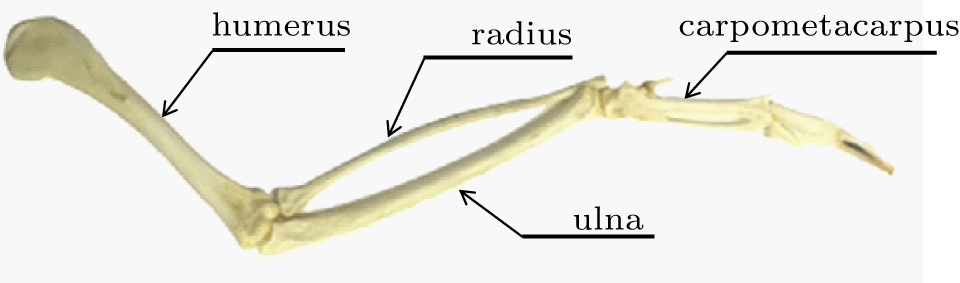 | Fig. 4. Photograph of the bones in the left wing of a turkey vulture.[30] |
 | Fig. 5. A sketch of simplified arms and joints on the photo of an eagle photographed in Thousand-Island Lake, Hangzhou. |
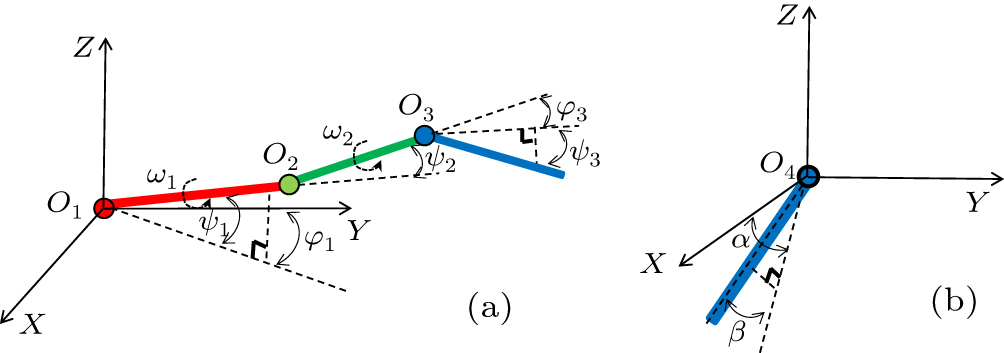
The skeleton structure was described as a three-jointed arm system along the quarter-chord line of a wing. The orientation of each arm can be changed by pitching the trunk and rotating around the corresponding joint.[31] As shown in Fig.
Another simple skeleton structure was described as a one-jointed arm system to represent the border line of the tail, although no skeleton exists in tail feathers. Take the right tail arm as an example as shown in Fig.
Each bone of a bird was treated as a rigid body connected by the corresponding joint, whereas the skin was flexible with morphing abilities.[33] The position and kinematics of the quarter-chord line of a wing to a fixed body coordinate system was described by a simplified arm, the arm motions were represented by the motion of floating frame of reference.[34] The total generalized coordinates of the i-th rigid body is qi = [xi,yi,zi,ϕi,θi,ψi]T, where [xi,yi,zi]T are locations of a body, [ϕi,θi,ψi]T are Euler angles.[34] When a body moves with both rotations and translations, a point P location of body i can be written as
 |
 |
 |
A 2D flight was assumed in the perpendicular plane, the equations of motion of an eagle were given in the ground coordinate system as follows:
 |
 |
 |
 |
 |
 |
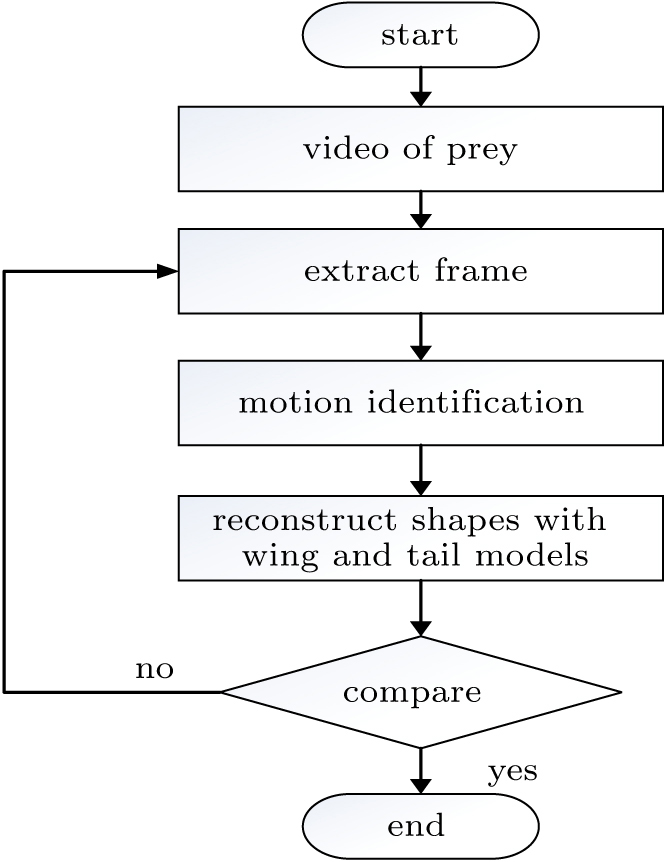
To capture the perching sequences, the flying video was recorded with high-speed camera with the help of Zhejiang Museum of Natural History, as shown in Fig.
It is lucky that an eagle B was still kept during the whole perching of eagle A. thus, it is convenient to locate a ground coordinate system at the foot of eagle B, as shown in Fig.
To predict the eagle motions during perching, unsteady aerodynamics at each time step was calculated by the method described in Subsection
A BFGS optimization method was used to reconstruct and predict the eagle motions by combining an objective function with the derivative-free line search method based on the approximate norm descent condition as shown in Fig.
 |
Equations (
| Table 1. Coefficients for the bionic airfoil. . |
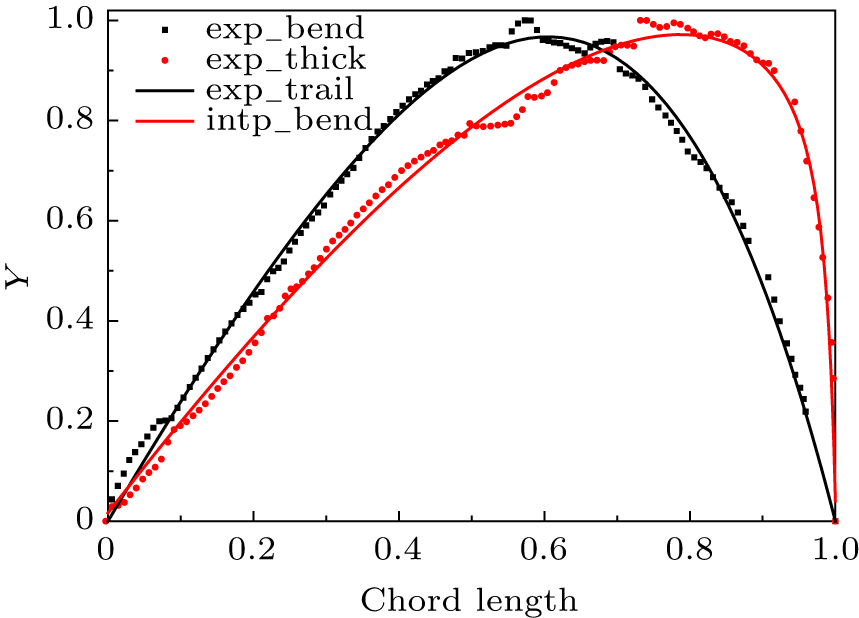
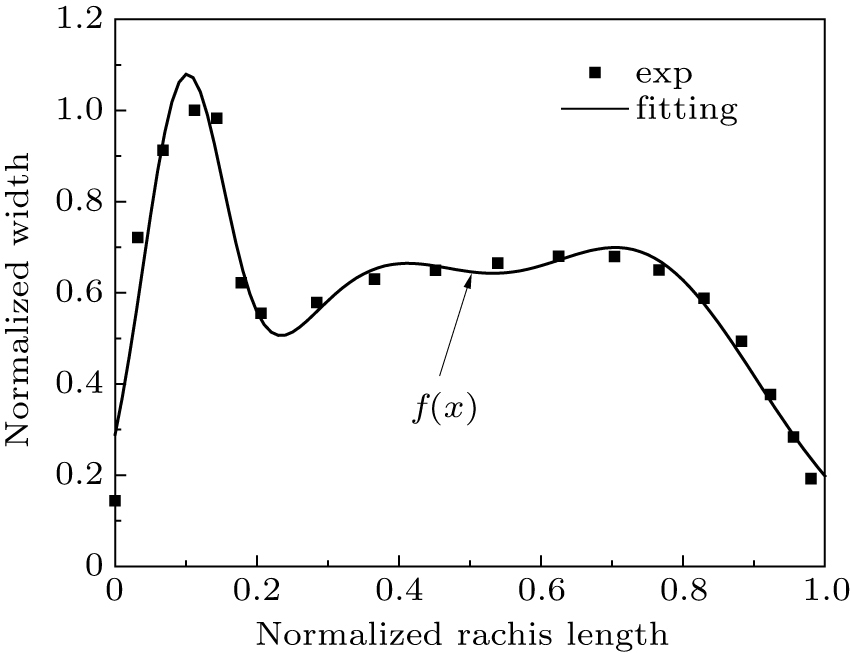
An optimized width distribution of a flight feather was obtained with Gaussian functions as
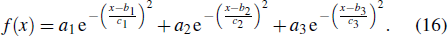 |
| Table 2. Coefficients of flight feather. . |
Figure
Figure
A wild Haliaeetus Albicilla was chosen for the present flight study. Both the flying abilities and the somatotypes of the Haliaeetus Albicilla compare favorably with those of the Aquila Chrysaetos. The bird mass was estimated to be 2.0 kg approximately as a matter of experience, and a span was estimated to be 2.0 m from left wingtip to wingtip which is close to the scanned Aquila Chrysaetos. The photography was taken with the help of Zhejiang Museum of Natural History. The recording was obviously not to pose any risk of causing pain, damage of harm to the wild animal involved.
The conventional design objectives or optimization objectives are usually the high lift-drag ratio. However, the key to the high manoeuvrability in bird flight lies not in the high lift-drag ratio or high lift performances, but in the way the wing morph to change the flying situations. Gliding, fighting, perching, and preying, etc. are the irrefutable proofs of this high manoeuvrability. Perching is one of the simplest wing motions with both the body attitude and flying attitude changed,[25] and the perching motions of a Haliaeetus Albicilla was studied in the present study as shown in Fig.
The experimental (Exp), fitted (Fit), and predicted (Pre) eagle displacements and velocities (Exp) were compared and illustrated in Fig.
 | Fig. 15. Comparison of the eagle motions with the experimental method (Exp), fitting approach (Fit), and predicting method (Pre): (a) displacement, (b) velocity. |
| Table 3. Coefficients for the fitted polynomials. . |
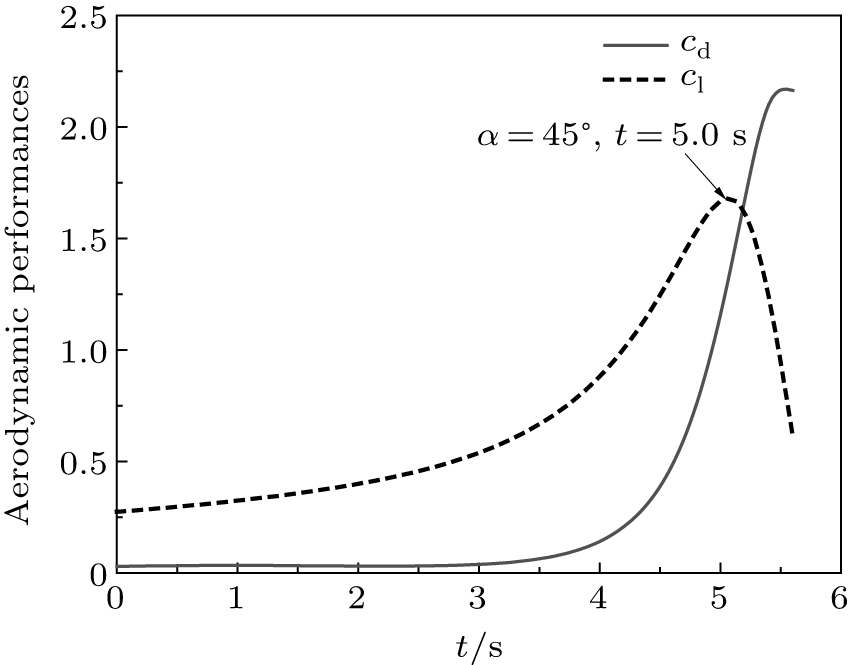
The corresponding velocity were obtained by taking the derivative of these two equations. All the fitted displacements and fitted velocities agree well with the experimental data. The predicted drag coefficient cd and lift coefficient cl were compared in Fig.
 |
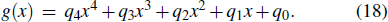 |
The eagle shapes were reproduced with the construction method discussed in the present study.[45] At the initial time, a small twist angle of wing and a small pitch angle of tail were observed. On the contrary, both the extending angles of tail feathers and the first primary feathers were obtained to be extremely large. As a result, ω2 and β were set as 7° and 3°, while α and φ3 were set as 50° and 10°, respectively. The constructed shape was compared with the corresponding photograph as shown in Fig.
 | Fig. 17. Comparison of eagle photographs and the reconstructed shapes during perching: (a) 0.0 s, (b) 2.0 s, (c) 3.0 s, (d) 4.0 s, (e) 4:48 s, (f) 5:36 s. |
On the other hand, the extending angle of the first primary feathers remained almost the same. At t = 3.0 s, ω2 and β were estimated to increase to 18° and 8°, respectively. With a larger twist angle of wing, a larger pitching moment was estimated. Therefore, the eagle was raised up to achieve a better brace position for landing. At time 4.0 s, the eagle tried its best to stretch both the wing and tail straight to increase drags as much as possible. Also, the pitch angle of the body was adjusted to undergo deep stall. It is interesting to find that a large anhedral angle of the wing was observed, and an anhedral angle with 20° was used to reconstruct the eagle shape. At 4.8 s, the tail stuck up to prevent striking the ground, and a β angle with −20° was used. At 5.6 s, the eagle perched, both wing and tail began to shrink, a backswept angle with about 15° was used in wing shape construction, α and β were increased set as 30° and −40°, respectively. Above all, the constructed shapes fit well with the photographs of each frame.
The flying of perching of a Haliaeetus Albicilla was recorded to study the wing and tail motions. It is interesting that a Haliaeetus Albicilla was observed to land on the ground without running or wing flapping but with combined morphing of wing and tail to achieve the soft landing.
To reveal the morphing sequences of the eagle, a shape reconstruction method was proposed to describe wing contours and tail contours based on the scanned surface geometry of another Aquila Chrysaetos. The wing and tail geometries were constructed by the extracted wing planform, chord distribution and twist distribution. Thereafter, multi-body dynamics was used to derive the kinetics equations of birds using seven-DOF wing skeleton and two-DOF tail skeleton. The Aquila Chrysaetos model was activated to replicate the perching. Finally, perching sequences of the eagle were extracted from the video, and perching motions were estimated and fitted with polynomials. A BFGS optimization method was established and was successfully applied to predict the perching motions. Above all, the constructed shapes fit well with the photographs of each frame with the coupled method of shape reconstruction, multi-body dynamics and BFGS optimization.
Based on the observations in the present study, the rapid pitch-up motions of the wing were found to cushion the direct impact to the ground, which is different from the man-made aircrafts. It is an irrefutable proof that the key to the high manoeuvrability in bird flight lies not in the high lift-drag ratio or high lift performances, but in the way in which the wing morph to change the flying situations. Moreover, state of art of the multi-body model with more than 18 DOF of an eagle, as well as the vortex interactions of wings and tail, are considered to be the most important in morphing flies. More attention should be paid to these issues in the future research. Above all, it can be expected that the present results are a good suggestion for aerodynamics learning of birds and the next-generation unmanned aerial vehicle design.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] |