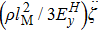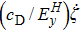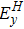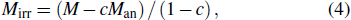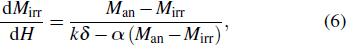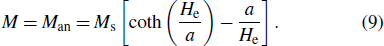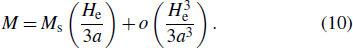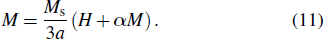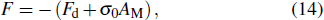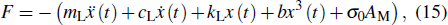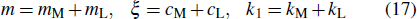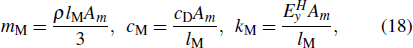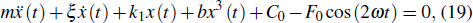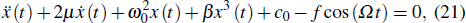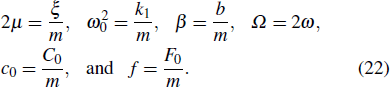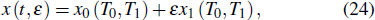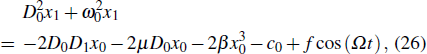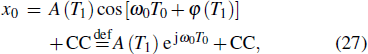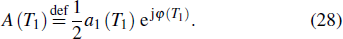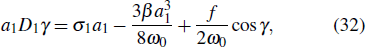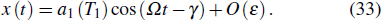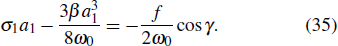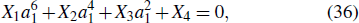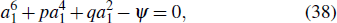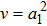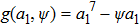Bifurcation and chaos characteristics of hysteresis vibration system of giant magnetostrictive actuator
1. IntroductionThe giant magnetostrictive actuator (GMA) is a device, which is fabricated by using the giant magnetostrictive material (GMM) as the core component to convert the magnetic energy and the mechanical energy.[1] These devices possess a wide variety of applications, including driving electro-hydraulic servo valves,[2,3] vibration control,[4–6] energy harvesting,[7–9] electronically controlled injectors,[10,11] and others.[12–14]
However, studies show that the GMM rod has a nonlinear hysteresis characteristic so that there is a hysteresis phenomenon between input current and output displacement of the GMA, which seriously damages the nonlinear stability of the GMA.[15–17] There are nonlinear instability and even chaotic motion in the GMA so that neither the long-term prediction nor long-term control of the GMA is almost possible. This drawback seriously hinders the application of the GMA in numerous fields, including the vibration control and energy collection. In order to break through this limitation, different methods, including the robust control,[18,19] adaptive control algorithm,[20] optimal control,[21] and the H∞ control[22] have been proposed so far. Therefore the influence of nonlinear factors is reduced and the GMA stability is improved.
Haomiao et al.[23] proposed a one-dimensional nonlinear magneto–thermal–mechanical coupling constitutive model for a GMM under multiple physical loads. Although the proposed model reflects the actual working condition of the material within a certain range, it cannot reflect the magnetic saturation nor hysteresis of the material. Tan and Baras[24] replaced the Jiles–Atherton (JA) model with the phenomenological model of the Preisach operator. Although this innovation enhances the versatility of the model, it requires complicated calculations and defines a large number of non-physical parameters. Yuchuan et al.[25] proposed a method to evaluate the static and dynamic characteristics of GMAs with hysteresis loops. Moreover, Huifang et al.[26] proposed a dynamic nonlinear multi-field coupling model for precise magnetostrictive actuators. The proposed design was based on the nonlinear piezomagnetic equation, JA hysteresis model, quadratic domain rotation model, and the GMA structural dynamics principle. The combined model is a low-order ordinary differential equation.
It should be indicated that the chaotic motion is a typical form of the motion in a nonlinear phenomenon. On the other hand, chaos phenomena are a hotspot of research on current nonlinear science. In fact, it has been considered to be one of the major discoveries of the 20th century since the advent of quantum mechanics, relativity and genes.[27] At present, the bifurcation and chaos characteristics can be analyzed by variational principle,[28–31] Melnikov method,[32,33] multi-scale method, etc.[34–36] Zeng[37] investigated the nonlinear chaotic motion in the GMA system. Moreover, Sun et al.[38] conducted numerical simulations to study the phenomenon of double-cycle and double-folding bifurcation of the transducer system under a certain equivalent spring stiffness and damping coefficient. Yuan et al.[39] performed numerous numerical simulations and found that the vibration system of the giant magnetostrictive transducer has complicated bifurcation and chaotic behavior. However, they did not study the regularity of the chaotic motion characteristics when parameters of the GMA system are varying. Moreover, they formed neither a systematic design method nor a theoretical basis. In fact, the stability design of the best matching model for multi-parameters of the GMA structure has not been explored so far. Reviewing the literature indicates that few researches have been carried out so far on the bifurcation and chaos of the GMA hysteresis vibration systems. On the other hand, majority of these researches have been performed on the bifurcation and chaos of other nonlinear vibration systems.[40–48]
In the present work, we initially introduce the working principle of the GMA, establish the mathematical model for hysteresis vibration system of the GMA and then analyze the bifurcation characteristics of the system. Finally, the bifurcation diagram, time domain waveform, phase portrait, and Poincaré mapping diagrams are used to analyze the chaotic motion characteristics of the system. In the present study, the method of the bifurcation and chaos of the GMA hysteresis nonlinear vibration system is proposed and its theoretical basis is established. It should be indicated that the research results of this study provide theoretical basis and technical support for the structural stability design of the GMA.
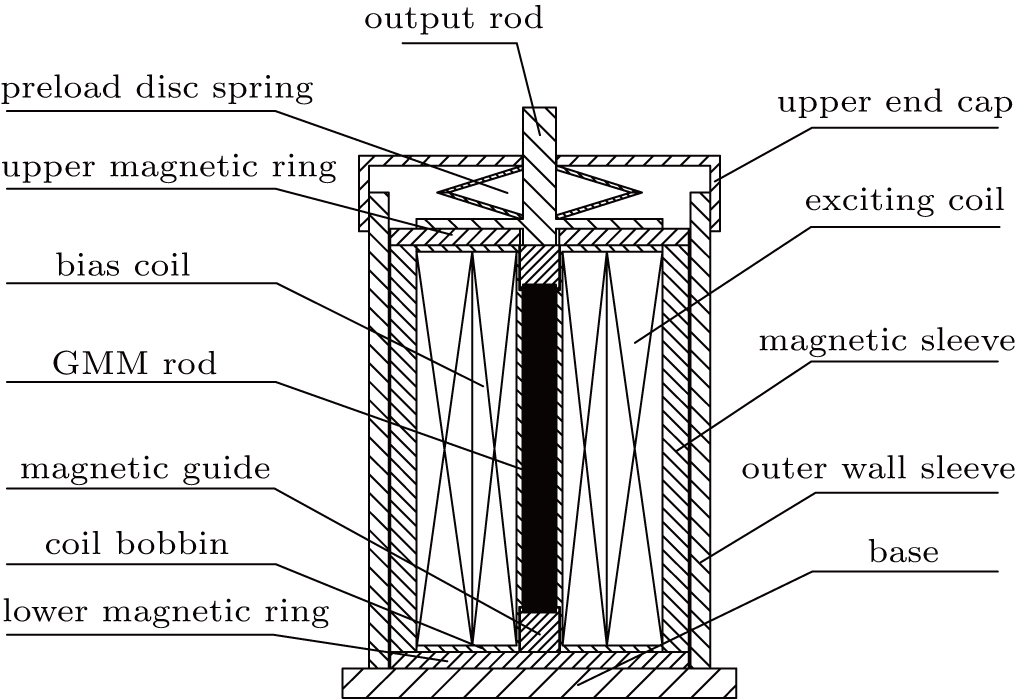
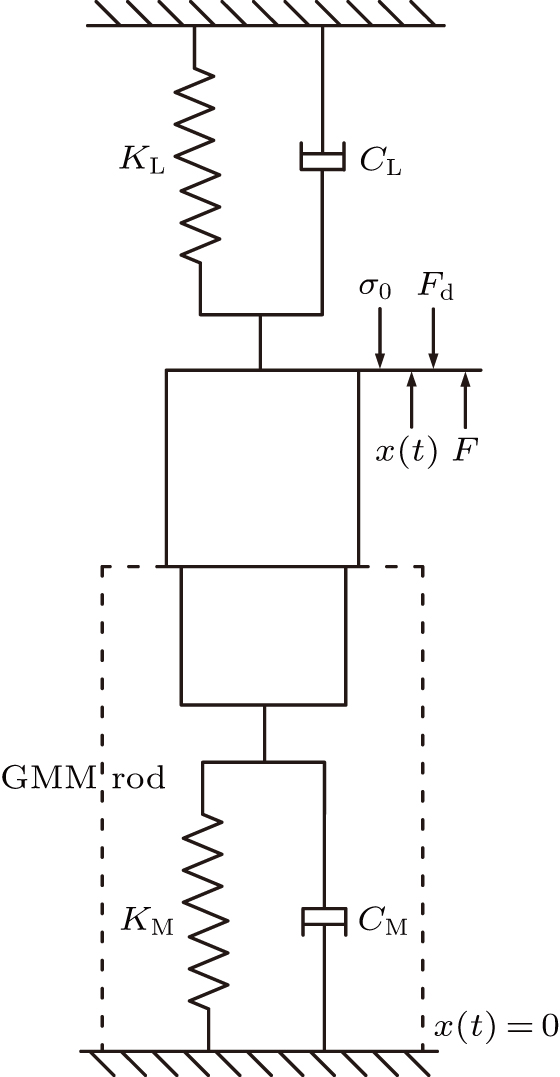
2. Working principle of GMAFigure 1 illustrates the structure of the GMA. The working principle can be described as follows. The input current of the exciting coil is adjusted to generate a driving magnetic field for controlling the elongation of the GMM rod. Then, the offset magnetic field generated by the DC current is used to eliminate the frequency doubling of the GMA. Moreover, the disc spring pretension structure is utilized to exert the pressure on the GMM rod so that it can achieve higher expansion. The magnetically permeable sleeve, ring and the sheet are used to form a closed magnetic circuit, which reduces the magnetic leakage and the interference of external magnetic devices in the drive.
3. Mathematical model of GMA hysteresis vibration systemThe GMA can be regarded as a combination of a single-degree-of-freedom mass elastic damping system and a second-order mass elastic damping system based on their working principle. Figure 2 shows a GMA equivalent mechanical system.
It is assumed that the axial length of the GMM rod and the axial length of coil are the same and the internal strain ζ, stress σ, and the magnetic field strength H are uniform. During the movement of the GMA system, the GMM rod has no displacement at one end and the same displacement x(t), velocity
, and acceleration
at the other end as the load is applied. Under the action of the exciting coil and the nonlinear disc spring and considering the mass and damping coefficient of the GMM rod, the nonlinear piezomagnetic equation with hysteresis can be obtained below. The total strain ζ of the GMM rod is the sum of the elastic strain
of the GMM rod, originating from the applied stress, the magnetostrictive strain λ with hysteresis caused by the applied magnetic field, the strain
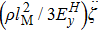caused by the GMM rod quality, and the strain
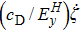caused by the internal damping coefficient of the GMM rod. Therefore, the total strain ζ of the GMM rod can be mathematically written as[49]
where
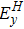
and
λ are the elastic modulus of the magnetic field and the magnetostrictive strain of the GMM rod, respectively. Furthermore,
lM,
cD, and
ρ denote the effective length, internal damping coefficient, and the mass density of the GMM rod, respectively. The approximate correlation between the magnetostrictive strain
λ of the isotropic material and the magnetization
M can be defined, based on the quadratic domain rotation model, as
[50]
where
λs and
Ms indicate the saturation magnetostriction coefficient of an isotropic material, saturation magnetization, respectively. Moreover,
M is the total magnetization generated by the exciting magnetic field, which is composed of the reversible magnetization
Mrev and the irreversible magnetization
Mirr.
By neglecting the crystal anisotropy, the Jiles–Atherton nonlinear hysteresis model can be expressed as[51,52]
The parameters from Eq. (
3) to Eq. (
8) are listed in Table
1.
Table 1.
Table 1.
 Table 1. Parameters appearring in Eqs. (3)–(8). .
| Man |
Non-hysteresis magnetization |
| He |
effective magnetic field inside the GMM |
| H0 |
excitation magnetic field amplitude |
| α |
equivalent parameter of internal magnetic domain interaction of GMM rod |
| a |
hysteresis magnetization shape parameter |
| c |
reversible coefficient |
| k |
irreversible loss coefficient |
| χr |
influence factor of the internal magnetic field distribution of the material |
| ω |
frequency of excitation magnetic field |
| δ |
symbol constant of magnetic field direction |
| Table 1. Parameters appearring in Eqs. (3)–(8). . |
When the hysteresis loss of the ferromagnetic material is in an ideal state, there is no energy loss and the total magnetization M is equal to the hysteresis magnetization Man. This can be expressed as
Taylor expansion of Eq. (
9) results in the following equation
By substituting high-order term into Eq. (7) the following equation is obtained
Therefore, the following equation can be obtained:
For the force analysis, the force acting on the GMM rod is described as follows:
where
mL,
cL, and
kL denote the equivalent mass, equivalent damping coefficient, and equivalent stiffness coefficient of the load, respectively. Moreover,
Fd and
b are the output force of the load and the third stiffness coefficient of disc spring term, respectively.
According to Newton’s third law,
where
F and
σ0 are the output force of the GMM rod and the applied pre-stress, respectively. Moreover,
AM is the equivalent cross-sectional area of the GMM rod.
Integrating Eqs. (13) and (14) results in the following equation:
where
mM,
cM, and
kM are equivalent mass, equivalent damping coefficient, and equivalent stiffness coefficient of the GMM rod, respectively.
The GMA hysteresis vibration equation is obtained by combining the strain ζ = x/lM with Eqs. (1) and (15) in the following form:
where
with
and
m,
ξ, and
k1 being the sum of the equivalent mass of the load and the equivalent mass of the GMM rod, system damping coefficient, and the system stiffness coefficient of the GMA hysteresis nonlinear vibration system, respectively.
When equations (2), (8), and (12) are substituted into Eq. (16), the simplified equation is written as follows:
where
with
F0 denoting the exciting force of the GMA system.
4. Bifurcation characteristics analysis of hysteresis vibration system of GMAEquation (19) is normalized and the left- and right-hand sides are both divided by m and the resulting equation is
where
The nonlinear term in Eq. (
21) is preceded by a small parameter
ε, then the resulting equation is given as follows:
The following approximate solution is obtained by the multi-scale method below:
[53]
where
Ti =
εit (
i = 0,1).
When equation (24) is substituted into Eq. (23), the resulting linear partial differential equation is similar to ε power factor and is given below:
where
Dn =
∂/
∂ Tn (
n = 0, 1).
In order to obtain the general solution of Eq. (25), it is assumed that
where CC is the conjugate of the preceding paragraph. Moreover,
A(
T1) is defined as
When the external excitation frequency
Ω nears the natural frequency
ω0 (
Ω =
ω0) of the system, detuning parameter
σ is obtained to be
The substitution of Eqs. (
27) and (
29) into Eq. (
26) eliminates long-term expressions and results in the following equation:
By substituting Eq. (28) into Eq. (30), the real and imaginary parts are obtained to be
where
γ =
σ T1 −
φ.
Equations (31) and (32) can be combined to obtain a1, γ, and the zero-order approximate solution of the nonlinear hysteresis vibration equation of the GMA system, and the following equation is obtained:
For the solution of steady state motion, it is assumed that
D1 a1 = 0 and
D1 γ = 0 in Eqs. (
31) and (
32)
The sum of the square of Eqs. (
34) and (
35) is added to obtain the bifurcation response equation of the GMA hysteresis nonlinear vibration system
where
Equation (
36) can be re-written as follows:
where
Since equation (
38) does not have
Z-axis symmetry, it is multiplied by
a1 to obtain the following equation:
Equation (40) satisfies G(−a1, ψ) = −G(a1, ψ), and thus has Z-axis symmetry. Assuming that
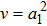, the following equation is obtained:
where
and
g(
a1,
ψ) ∈
εa1, ψ = (
Z). According to the singularity theory,
G(
a1,
ψ,
q,
p) is a universal opening of normative
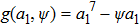
, where
p and
q are opening parameters and the singularity is the codimension 2.
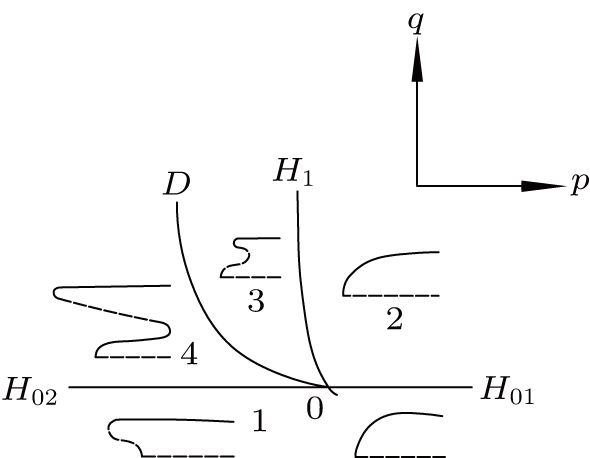
Figure 3 illustrates the transition set and branch topology of the system.
1: Bifurcation point set: B(Z) = φ (φ is an empty set);
2: Lag point set: H01(Z) = {q = 0,p > 0}; H02(Z) = {q = 0, p < 0}; H1(Z) = {q = p2/3, p ≤ 0};
3: Double limit point set: D(Z) = {q = p2/4, p ≤ 0};
4: Transition set: ∑ = B ∪ H ∪ D.
5. Numerical simulationFor Eq. (19), the following values are obtained: m = 1, ξ = 0.5, k1 = −1, b = 1, C0 = 1.5, F0 = 1, and ω = 1. Moreover, the initial value is taken to be (0, 0). Then, the range of value of each parameter in the GMA hysteresis nonlinear vibration system is determined by calculating the response of the GMA hysteresis nonlinear vibration system with the variation of each parameter. The time domain waveform, phase portrait, and Poincaré mapping diagram of each parameter in the GMA hysteresis nonlinear vibration system are drawn by the fourth-order Runge–Kutta method. Moreover, the chaotic motion characteristics of the system with the GMA hysteresis nonlinear vibration system damping coefficient, system stiffness coefficient, coefficient of cubic stiffness term of disc spring, exciting force, and the exciting frequency are studied.
5.1. Bifurcation characteristics of system and path to chaos when system damping coefficient changesFigure 4 shows the bifurcation diagram of the system variation as the damping coefficient ξ changes. The flowchart for leading the system to chaos when the damping coefficient ξ changes is as follows:
Periodic motion → jump motion → chaotic motion → paroxysmal chaos → degenerate into period 3→ chaotic motion → paroxysmal chaos → degenerate into period 4→ chaotic motion → paroxysmal chaos → degenerate into period 2→ periodic motion. The regions of system damping coefficient ξ are shown in Table 2.
Table 2.
Table 2.
Table 2. Regions of system damping coefficient ξ. .
| Ranges of ξ |
Motion form |
| (0.05, 0.215) |
periodic motion |
| (0.215, 0.38) |
chaotic motion (Fig. 5) |
| (0.38, 0.43) |
degenerate into period 3 |
| (0.43, 0.51) |
chaotic motion (Fig. 6) |
| (0.51, 0.55) |
degenerate into period 4 |
| (0.55, 0.61) |
chaotic motion |
| (0.61, 0.765) |
degenerate into period 2 (Fig. 7) |
| (0.765, 1.00) |
periodic motion |
| Table 2. Regions of system damping coefficient ξ. . |
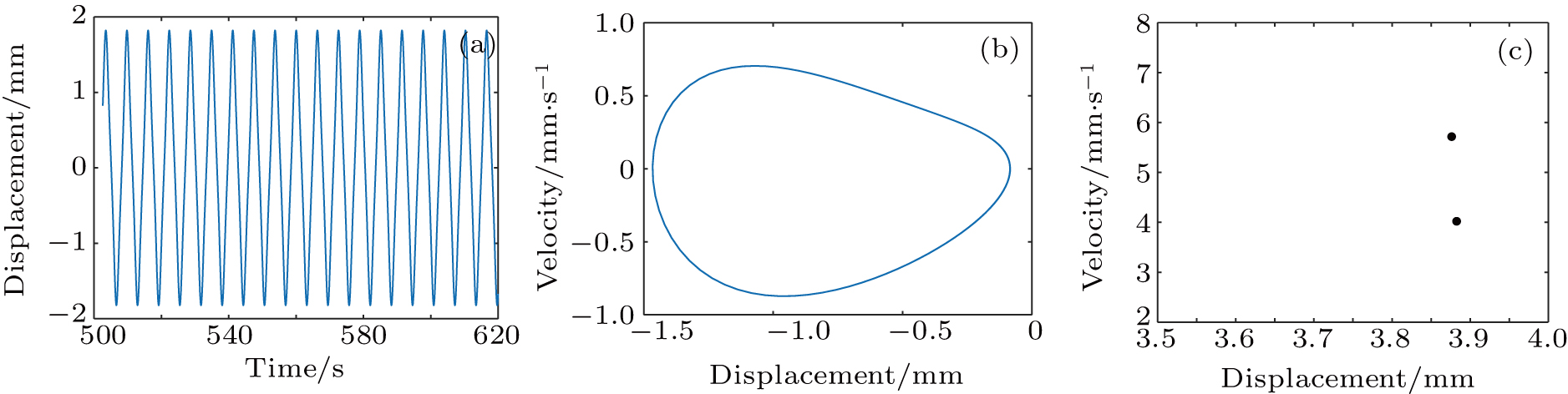
Figure 4 indicates that when the system damping coefficient is ξ ∈ (0.05, 0.215), the motion of the system obtains a steady-state period of 1. However, when the system damping coefficient ξ is greater than 0.215, the periodic motion of the system jumps. Moreover, figure 5 shows that when the system damping coefficient is ξ ∈ (0.215, 0.38), the system jumps from periodic motion to chaotic motion. Paroxysmal chaos occurs near the boundary from chaotic motion to regular motion. When the system damping coefficient ξ is about 0.38, the system generates paroxysmal chaos, which is accompanied by bifurcation degradation into a period of 3. When the system damping coefficient is ξ ∈ (0.38, 0.43), the system performs a motion with a period of 3. Furthermore, figure 6 shows that when the system damping coefficient is ξ ∈ (0.43, 0.51), the system is in chaotic motion. When the system damping coefficient is ξ ∈ (0.51,0.55), the system will again generate paroxysmal chaos, and then the system will present the period 4 motion. When the system damping coefficient is ξ ∈ (0.55, 0.61), the system performs chaotic motion. Moreover, when the system damping coefficient ξ is greater than 0.61, the system degenerates into the period 2 motion with the inverse bifurcation, and finally degenerates into a steady state with a period of 1. When the system damping coefficient is ξ ∈ (0.61, 0.765), the system performs a motion with a period of 2. Figiure 7 illustrates that when the system damping coefficient is ξ = 0.65, the phase portrait is a closed curve; the time domain waveform is regular and the period is stable. Moreover, it is observed that the Poincaré mapping diagram has two attracting points, so the system has a typical two-cycle motion. Finally, when the system damping coefficient is ξ ∈ (0.765, 1.00), the system performs a steady-state motion with a period of 1.
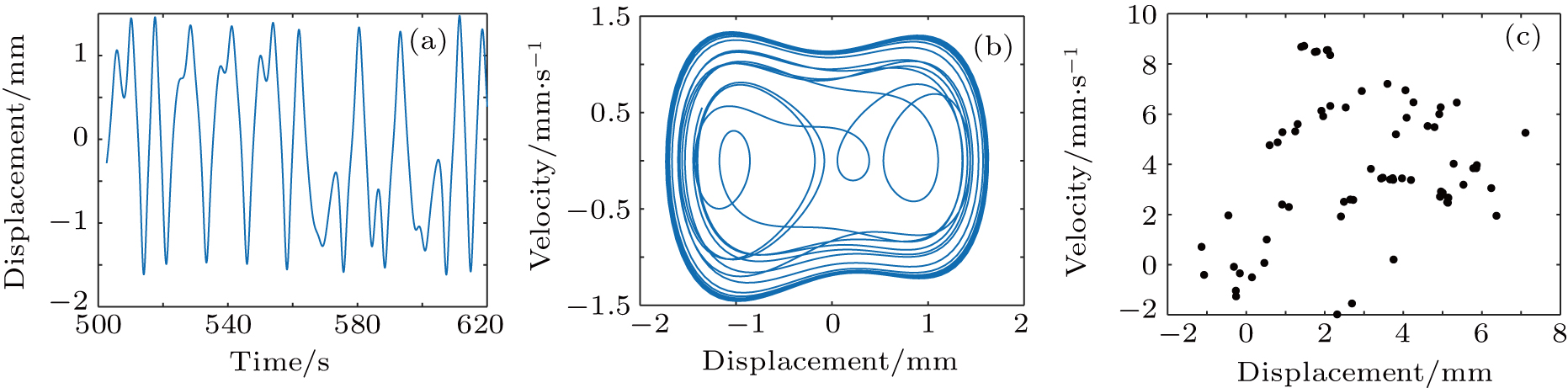
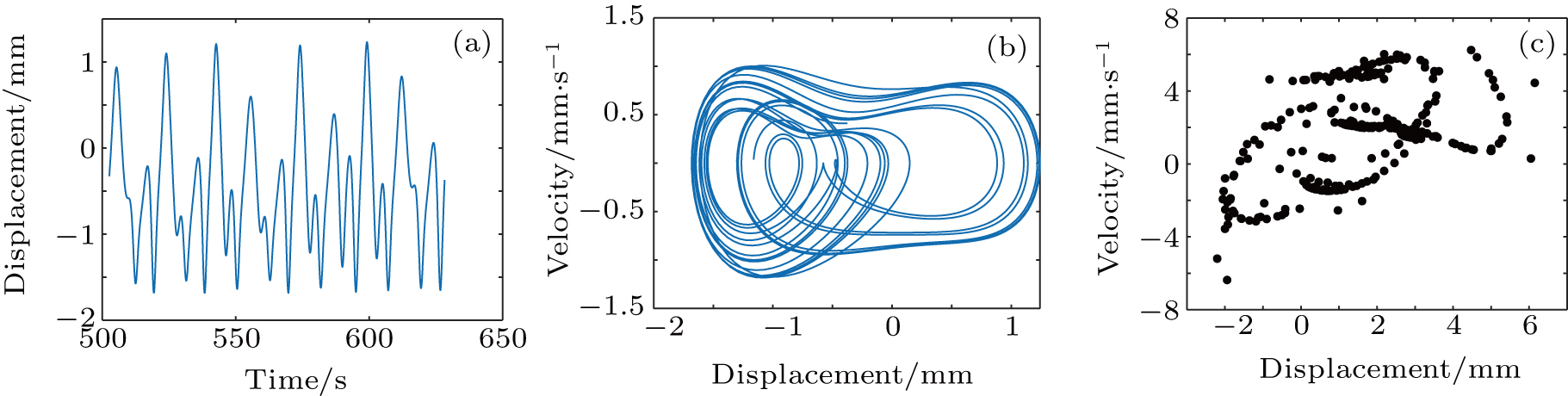
Figures 5 and 6 show the diagrams of time domain waveform, phase portrait, and Poincaré mapping for chaotic motion in the system when the system damping coefficientis ξ = 0.25 and ξ = 0.45, respectively. It is observed that the time domain waveform in Figs. 5(a) and 6(a) are irregular and the periodic vibration is unstable. Moreover, the phase portrait in Figs. 5(b) and 6(b) are both filled with the phase space and are not closed for a long time and do not overlap each other nor entangle each other. Furthermore, it is indicated that the Poincaré mapping diagram in Fig. 5(c) is neither a finite point set nor a closed curve, while the Poincaré mapping diagram in Fig. 6(c) is a lattice with a certain geometry. Therefore, it indicates that the system is in a chaotic state.
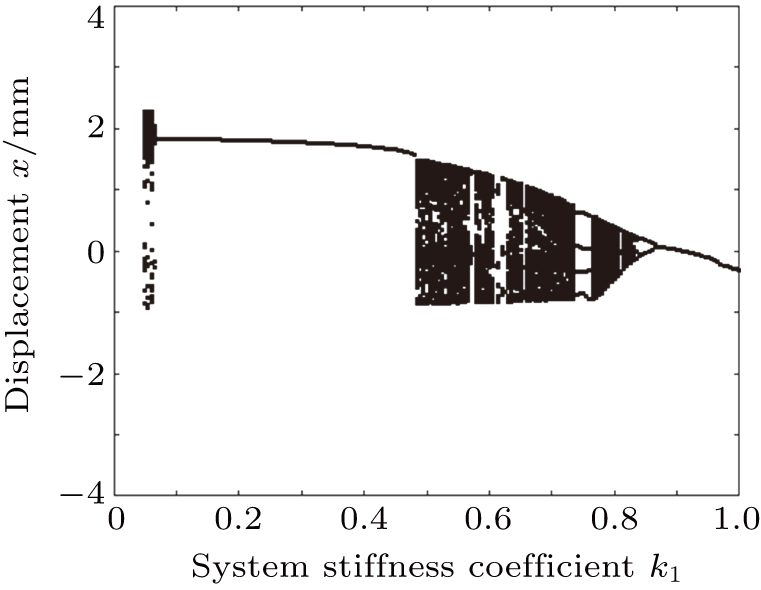
5.2. Bifurcation characteristics of system and path to chaos when system stiffness coefficient changesFigure 8 shows the bifurcation diagram of the system when the stiffness coefficient k1 changes. The flowchart that the system enters into chaos when the stiffness coefficient k1 changes indicates the following steps:
Chaotic motion → paroxysmal chaos → periodic motion → chaotic motion → paroxysmal chaos → period 4→ chaotic motion → paroxysmal chaos → period 2→ periodic motion. The regions of system stiffness coefficient k1 are listed in Table 3.
Table 3.
Table 3.
Table 3. Regions of system stiffness coefficient k1. .
| Ranges of k1 |
Motion form |
| (0.05, 0.07) |
chaotic motion |
| (0.07, 0.48) |
periodic motion |
| (0.48, 0.735) |
chaotic motion (Fig. 9) |
| (0.735, 0.765) |
period 4 (Fig. 10) |
| (0.765, 0.835) |
chaotic motion (Fig. 11) |
| (0.835, 0.865) |
period 2 |
| (0.865, 1.00) |
periodic motion |
| Table 3. Regions of system stiffness coefficient k1. . |
Figure 8 shows that when the system stiffness coefficient is k1 ∈ (0.05, 0.07), the system performs a chaotic motion. When the system stiffness coefficient is k1 ∈ (0.07, 0.48), the system performs a steady state period of 1 motion. Moreover, when the system stiffness coefficient k1 is 0.57, 0.62, and 0.67, the multiple burst chaos occurs in the system. Figure 9 indicates that when the system stiffness coefficient is k1 ∈ (0.48, 0.735), the system performs chaotic motion. Figure 10 indicates that when the system stiffness coefficient is k1 ∈ (0.735,0.765), the system degenerates from chaotic motion to motion with period 4. Furthermore, it is observed that when the system stiffness coefficient is k1 = 0.75, the phase portrait is a closed curve; the time domain waveform is regular and the period is stable. Moreover, the Poincaré mapping diagram has four attracting points, so the system is in a motion with a period of 4. Figure 11 illustrates that when the system stiffness coefficient is k1 ∈ (0.765, 0.835), the system performs chaotic motion. When the system stiffness coefficient k1 is greater than 0.835, the system degenerates into a period 2 motion with the inverse branching and finally degenerates into a steady-state motion with a period of 1. When the system stiffness coefficient is k1 ∈ (0.835, 0.865), the system performs a motion with a period of 2. Finally, when the system stiffness coefficient is k1 ∈ (0.865, 1.00), the system performs a steady-state motion with a period of 1.
Figures 9 and 11 show the diagram of time domain waveform, phase portrait and Poincaré mapping for the chaotic motion of the system when the system stiffness coefficient is k1 = 0.65 and k1 = 0.8, respectively. Figures 9(a) and 11(a) illustrate the non-period irregular reciprocating motion of the time domain waveform. Moreover, figures 9(b) and 11(b) show that the phase portraits are curves of a disordered multi-turn phase set. Furthermore, figure 9(c) shows that the Poincaré mapping diagram is linearly distributed by infinite points, while the Poincaré mapping diagrams in Fig. 11(c) is neither a finite point set nor a closed curve. Therefore, it indicates that the system is in a chaotic state.
Based on the aforementioned analysis, as the system damping coefficient (ξ) and the system stiffness coefficient (k1) increase, the system output state tends to be stable. Moreover, equations (17) and (18) indicate that the increasing of parameters cM and kM of the GMM rod can increase parameters ξ and k1 and enhance the system stability. Therefore, selecting an elongated GMM rod is disadvantageous for the stability. Meanwhile, the damping and rigidity of the disc spring can be appropriately increased accordingly.
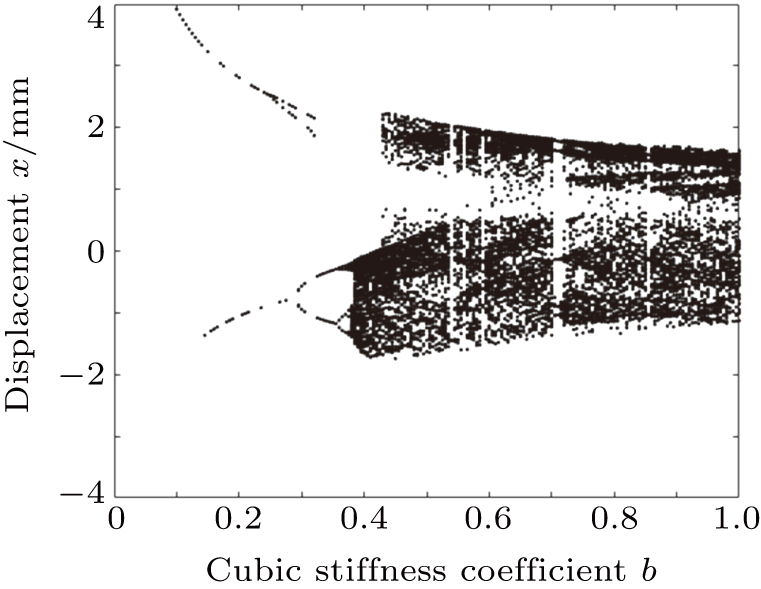
5.3. Bifurcation characteristics of system and path to chaos when coefficient of cubic stiffness term of disc spring changesFigure 12 shows that the bifurcation diagram of the system when the coefficient of cubic stiffness term of disc spring b changes. The flowchart leading the system to be chaotic when the coefficient of cubic stiffness term of disc spring b changes is written as follows:
Periodic motion → quasi-periodic motion → periodic doubling bifurcation → period 4→ multiple paroxysmal chaos → chaotic motion. The motion forms in different regions of coefficient of cubic stiffness with disc spring b are listed in Table 4.
Table 4.
Table 4.
Table 4. Motion forms in different regions of coefficient of cubic stiffness with disc spring b. .
| Ranges of b |
Motion form |
| (0.1, 0.145) |
periodic motion |
| (0.145, 0.275) |
quasi-periodic motion (Fig. 13) |
| (0.275, 0.355) |
periodic doubling bifurcation |
| (0.355, 0.38) |
period 4 |
| (0.38, 1.00) |
chaotic motion (Fig. 14) |
| Table 4. Motion forms in different regions of coefficient of cubic stiffness with disc spring b. . |
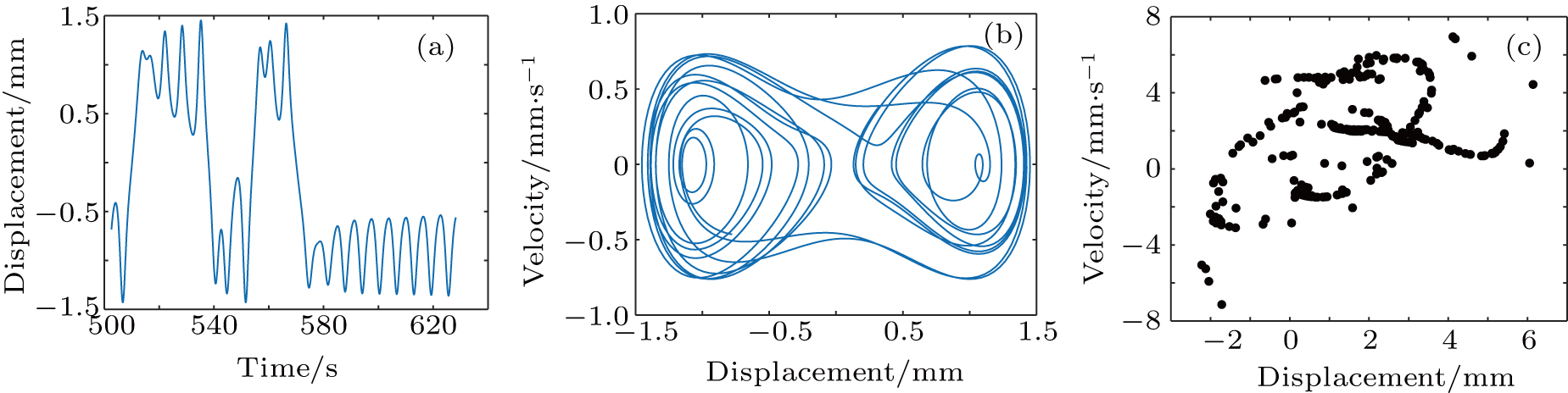
Figure 12 illustrates that when the coefficient of the cubic stiffness term of the disc spring is b ∈ (0.1, 0.145), the motion of the system is a motion with a steady-state period of 1. When the coefficient of the cubic stiffness term of the disc spring is b∈ (0.145, 0.275), the system switches from the steady-state periodic motion to the quasi-periodic motion. Moreover, figure 13 shows that when the coefficient of the cubic stiffness term of disc spring is b = 0.2, the phase portrait is filled with the phase space and it is closed. The time domain waveform is the superposition of two periodic signals, and the Poincaré mapping diagram is the finite point setforming a semi-closed curve, so the system is a quasi-periodic motion. When the coefficient of the cubic stiffness term of the disc spring is b∈ (0.275, 0.355), the pseudo-periodic motion of the system occurs with a period-doubling bifurcation. Furthermore, when the coefficient of the cubic stiffness term of the disc spring is b∈ (0.355, 0.38), the system period doubling is a period-4 motion. When the coefficients of the cubic stiffness term of the disc spring b are 0.54, 0.59, 0.71 and 0.86, multiple burst chaos occurs in the system. Figure 14 shows that when the coefficient of the cubic stiffness term of the disc spring is b∈ (0.38, 1.00), the system performs the chaotic motion.
Figure 14 shows the time domain waveform, phase portrait and Poincaré mapping diagram of the chaotic motion in the system when the coefficient of the cubic stiffness term of the disc spring is b = 0.5. Figure 14(a) shows that the time domain waveform is irregular and no periodic motion occurs. Moreover, figure 14(b) indicates that the phase portrait is filled with the phase space region and cannot be closed for a long time. It is observed that the phase portrait motion is a reciprocating motion and the period is an infinitely long motion. Furthermore, figure 14(c) illustrates that the Poincaré mapping diagram is neither a finite point set nor a closed curve. Therefore, it is indicated that the system is in a chaotic state.
Based on the above analysis, the system output state tends to be stable as the coefficient of cubic stiffness of the disc spring b increases.
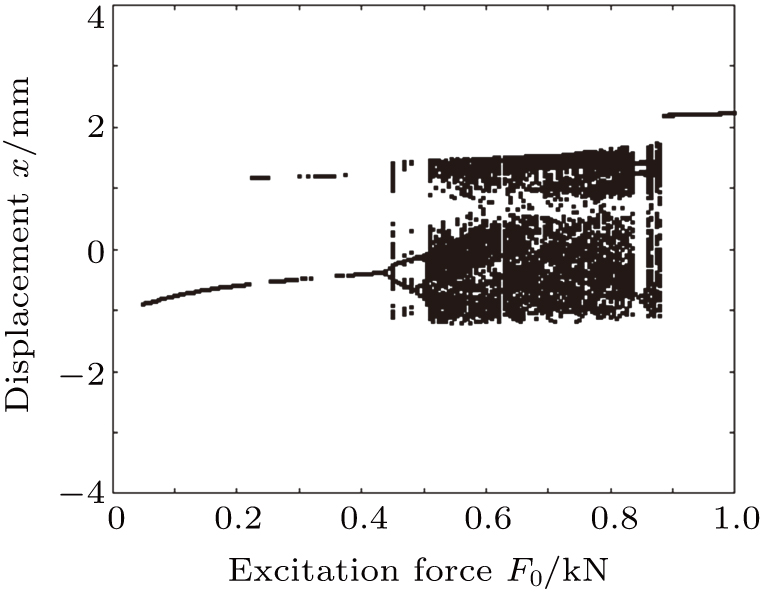
5.4. Bifurcation characteristics of system and path to chaos when exciting force changesFigure 15 shows the bifurcation diagram of the system when the exciting force F0 changes. The flowchart leading the system to be chaotic when the exciting force F0 changes is written asfollows:
Periodic motion → quasi-periodic motion → double period bifurcation → multiple paroxysmal chaos → chaotic motion → paroxysmal chaos → degenerate into period 3→ chaotic motion → jump motion → periodic motion. The motion forms in different regions of exciting force F0 are listed in Table 5.
Table 5.
Table 5.
Table 5. Motion forms in different regions of exciting force F0. .
| Ranges of F0 |
Motion form |
| (0.05, 0.225) |
periodic motion |
| (0.225, 0.44) |
quasi-periodic motion |
| (0.44, 0.51) |
double period bifurcation |
| (0.51, 0.835) |
chaotic motion (Fig. 16) |
| (0.835, 0.86) |
period 3 |
| (0.86, 0.88) |
chaotic motion |
| (0.88, 1.00) |
periodic motion (Fig. 17) |
| Table 5. Motion forms in different regions of exciting force F0. . |
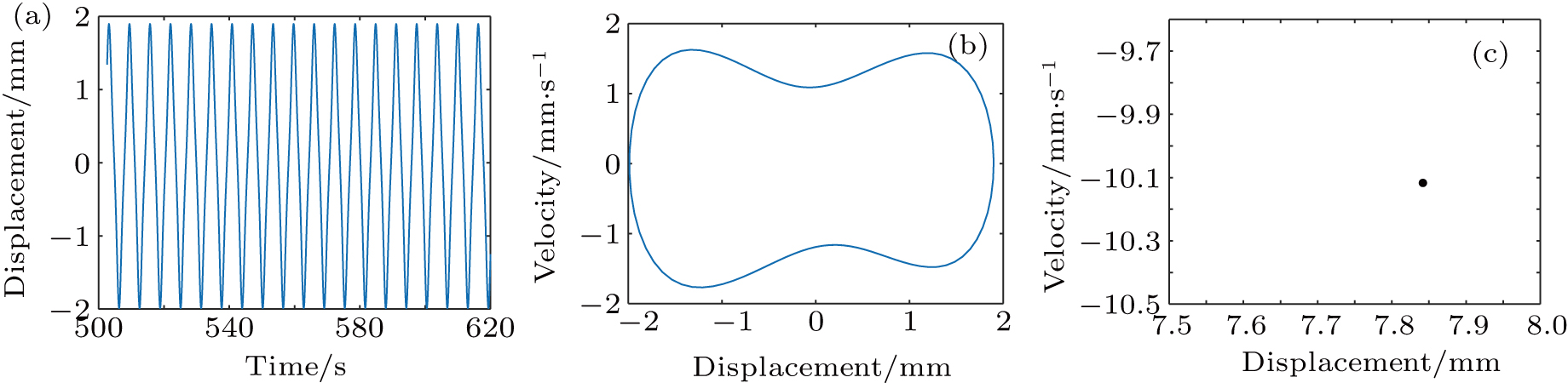
Figure 15 shows that when the exciting force is F0 ∈ (0.05, 0.225), the motion of the system has a steady-state period of 1. When the exciting force is F0 ∈ (0.225, 0.44), the system converts the steady-state periodic motion into the quasi-periodic motion. Moreover, when the exciting force is F0 ∈ (0.44,0.51), the pseudo-periodic motion of the system occurs in the period-doubling bifurcation. When the values of exciting force F0 are 0.45, 0.47, and 0.48, multiple episodic chaos occurs in the system. Figure 16 indicates that when the exciting force is F0∈ (0.51, 0.835), the system performs chaotic motion. When the exciting force F0 is about 0.835, the system again generates paroxysmal chaos and then enters into the motion with a period of 3. When the exciting force is F0∈ (0.835, 0.86), the system performs a motion with a period of 3. When the excitation force is F0∈ (0.86, 0.88), the system has a chaotic motion. Furthermore, when the exciting force F0 is greater than 0.88, the chaotic motion of the system jumps. Moreover, when the exciting force is F0∈ (0.88, 1.00), the system jumps from chaotic motion to steady-state motion with period of 1. Figure 17 shows that when the exciting force is F0 = 0.9, the phase portrait is a closed curve, the time domain waveform is regular and the period is stable. Moreover, it is observed that the Poincaré mapping diagram is an isolated point, so the system has a typical single-cycle motion.
Figure 16 shows the time domain waveform, phase portrait and Poincaré mapping diagram of the chaotic motion in the system when the exciting force is F0 = 0.55. Figure 16(a) illustrates that the time domain waveform is irregular and the periodic vibration is not stable. Moreover, figure 16(b) indicates that the phase portrait is filled with the phase space region and cannot be closed for a long time. It is observed that the phase portrait motion is a reciprocating motion and the period is an infinitely long motion. Figure 16(c) illustrates that the Poincaré mapping diagram is neither a finite point set nor a closed curve. Therefore, it is indicated that the system is in a chaotic state.
According to the foregoing analysis, as the excitation force F0 increases, the system output state becomes more unstable.
5.5. Bifurcation characteristics of system and path to chaos when excitation frequency changesFigure 18 shows the bifurcation diagram of the system when the excitation frequency ω changes. The flowchart leading the system to be chaotic when the excitation frequency ω changes is described as follows:
Multiple paroxysmal chaos → chaotic motion → paroxysmal chaos → degenerate into period 2→ chaotic motion → paroxysmal chaos → periodic motion → chaotic motion → paroxysmal chaos → periodic motion. The motion forms in different regions of excitation frequency ω are given in Table 6.
Table 6.
Table 6.
Table 6. Motion forms in different regions of excitation frequency ω. .
| Ranges of ω |
Motion form |
| (0.05, 0.465) |
chaotic motion |
| (0.465, 0.59) |
period 2 |
| (0.59, 0.645) |
chaotic motion (Fig. 19) |
| (0.645, 0.67) |
periodic motion |
| (0.67, 0.72) |
chaotic motion |
| (0.72, 1.00) |
periodic motion |
| Table 6. Motion forms in different regions of excitation frequency ω. . |
Figure 18 shows that when the excitation frequency is ω ∈ (0.05, 0.465), the system enters into the chaotic motion after multiple bursting chaos has occurred. When the excitation frequency ω is about 0.465, the system again undergoes the paroxysmal chaos and then enters into the motion of period 2. Moreover, when the excitation frequency is ω ∈ (0.465,0.59), the chaotic motion of the system occurs in a period-doubling bifurcation and enters into a motion with a period of 2. When the excitation frequency is ω ∈ (0.59, 0.645), the system performs a chaotic motion. Figure 19 (ω = 0.6) shows that when the excitation frequency is ω ∈ (0.645, 0.67), the system exhibits a short-term periodic motion. Moreover, when the excitation frequency is ω ∈ (0.67, 0.72), the system obtains a chaotic motion. Finally, when the excitation frequency is ω ∈ (0.72, 1.00), the system performs a steady-state motion with a period of 1.
Figure 19 shows the time domain waveform, phase portrait and Poincaré mapping diagram of the chaotic motion in the system when the excitation frequency is ω = 0.6. Figure 19(a) shows that the time domain waveform is irregular and the periodic vibration is unstable. Moreover, figure 19(b) illustrates that the phase portrait is filled with the phase space region and cannot be closed for a long time. It is observed that they do not overlap each other and are entangled with each other. Furthermore, figure 19(c) indicates that the Poincaré mapping diagram is neither a finite point set nor a closed curve. Therefore, it is indicated that the system is in a chaotic state.
6. Conclusions and perspectives(i) The mathematical model of the hysteresis nonlinear vibration of the GMA system is established by analyzing the working principle of the GMA. Moreover, the vibration equation of the GMA system is described.
(ii) The output response of the GMA hysteresis nonlinear vibration system is simulated, and the range of values of each parameter is determined when the periodic solution is generated. Moreover, the system damping coefficient possesses a periodic characteristic in the intervals (0.05, 0.215), (0.38, 0.43), (0.51, 0.55), (0.61, 0.765), and (0.765, 1.00). The system stiffness coefficient has a periodic property in the intervals (0.07, 0.48), (0.735, 0.765), (0.835, 0.865), and (0.865, 1.00). Moreover, the coefficient of the cubic stiffness term of the disc spring indicates a periodic behavior in the intervals (0.1, 0.145) and (0.355, 0.38). Furthermore, the exciting force presents a periodic property in the intervals (0.05, 0.225), (0.835, 0.86), and (0.88, 1.00). Finally, the excitation frequency is periodic in the intervals (0.465, 0.59), (0.645, 0.67), and (0.72, 1.00).
(iii) The dynamic simulation analyses of the GMA system are conducted for different values of characteristic parameter. The analysis is performed from a purely theoretical point of view. Increasing the system damping coefficient, increasing the system stiffness coefficient, increasing the coefficient of the square stiffness term of the disc spring, reducing the coefficient of the cubic stiffness term of the disc spring, reducing the exciting force and increasing the excitation frequency all can effectively compress the chaotic motion range of the system and increase the periodic motion range of the system, thus improving the stability of the GMA system.
(iv) In the present study, the theoretical basis of the bifurcation and chaos characteristics of the GMA for hysteresis nonlinear vibration systems is established. It is found that changing the characteristic parameters can cause the GMA system to perform chaotic motion, or to avoid the chaotic motion, and can even control the vibration characteristics of the system. It should be indicated that the present study can provide the theoretical basis and technical supports for the structural stability design of the GMA.
