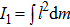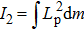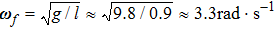1. IntroductionThe Newtonian gravitational constant G is one of the most fundamental and universal constants, which is closely related to theoretical physics, astrophysics, and geophysics, while its precision is the lowest so far.[1–5] Although the precision of G has been improved over the past few decades, the values in CODATA 2014 are still in poor agreement because of the extreme weakness and nonshieldability of gravity, which indicates that there may be some systematic errors that have not been discovered or correctly understood in the experiments.[6,7] At present, the best results of G measurement have been given by a group in Huazhong University of Science and Technology (HUST), who reported two independent values of G using torsion pendulum experiments with the time-of-swing method[4,8–10] and the angular acceleration method.[1,11,12] The G values given by these two experiments are 6.674184 × 10−11 m3 · kg−1 · s−2 and 6.674484 × 10−11 m3 · kg−1 · s−2, with relative standard uncertainties of 11.64 ppm and 11.61 ppm, respectively.[13]
The effect of the Earth’s rotation[6,14,15] on G measurement has been roughly estimated to be very small before, but it is necessary to conduct a comprehensive and detailed modeling for it, which may be helpful for the G measurement with higher accuracy in the future. In the G measurement with the angular acceleration method, the effect of the Earth’s rotation has been fully analyzed, but the analysis of this effect in the time-of-swing method is still missing. This work is to solve this problem. In this paper, we present the derivation of the Lagrangian of the torsion pendulum in the general relativistic frame. Based on this, the motion equations of the torsion pendulum can be obtained. With the correlation method[16–18] and the numerical simulation in MATLAB, we extract the periods of the torsion pendulum before and after adding the perturbation brought by the Earth’s rotation, respectively. From the difference of the periods, the effect of the Earth’s rotation on measuring G can be obtained. This study shows that the influence of the Earth’s rotation mainly contributes to the G measurement by coupling itself with the pendulum motion of the torsion pendulum and if the amplitude of the pendulum motion is controlled at the milliradian level, the Earth’s rotation only contributes an uncertainty about 10−3 ppm to the G value.
The outline of this paper is as follows. Section 2 briefly introduces the principle of measuring the gravitational constant G with the time-of-swing method. In Section 3, the Lagrangian expression of the torsion pendulum is derived in detail in the relativistic frame. In Section 4, we obtain the motion equations of the torsion pendulum from the Lagrangian, and estimate the influence of the Earth’s rotation on G measurement with the correlation method. Finally, the paper is concluded in Section 5.
2. The principle of the time-of-swing methodLet us have a simple review on the principle of the time-of-swing method. The time-of-swing method was proposed by Braun in the 1890s and developed by Heyl, Cohen, and Taylor later,[19–22] which has been widely used to measure G now. In this method, a torsion pendulum is suspended by a very thin fiber, and two source masses are placed on opposite sides of the pendulum, as shown in Fig. 1. When the line connecting the source masses is parallel to the pendulum, namely, the near configuration, the attraction of the source masses to the pendulum provides an additional positive restoring torque, so that the total restoring torque increases. This leads to the increase of the torsional oscillation frequency and the decrease of the torsional oscillation period. In contrast, when the line connecting the source masses is vertical to the pendulum, namely, the far configuration, the attraction of the source masses to the pendulum provides an additional negative restoring torque, so that the total restoring torque decreases. This leads to the decrease of the torsional oscillation frequency and the increase of the torsional oscillation period.
In vacuum, when the source masses are placed around, the motion equation of the torsion pendulum can be written as[23,24]
where
I denotes the moment of inertial of the torsion pendulum,
θ is the deflection angle,
k is the fiber torsion constant,
GCg is the effective gravitational torsion constant, and
Cg is the coupling constant determined by the mass distributions and positions of the pendulum and source masses. From Eq. (
1), we can obtain the period of the torsion pendulum as
Based on the two configurations mentioned above, two different periods
τn and
τf can be obtained, respectively. Therefore,
G can be determined by
3. The Lagrangian expression of the torsion pendulum in the general relativistic frameHere, we consider the influence of the Earth’s rotation on G measurement with the time-of-swing method. This section focuses on obtaining the motion equations of the torsion pendulum containing the Earth’s rotation. In order to achieve this, the Lagrangian expression of the torsion pendulum should be obtained first. We start from the relativistic expression of the Lagrangian density in any curvilinear coordinate system
with
gμ υ being the four-dimensional metric tensor and
c being the speed of light. In this work, we adopt the following convention: Greek (space–time) indices including
μ,
υ,
α, … will run from 0 to 3, and small Roman (spatial) indices
i,
j,
k, … will run from 1 to 3; that is,
x0 is considered as the time coordinate and
xi as the spatial one. In weak field approximation up to the Newtonian order,
gμ υ is usually split into the 3+1 formalism as
By substituting Eq. (
5) into Eq. (
4), the Lagrangian can be further expressed as
Usually, the external gravitational field of the Earth described by the Schwarzschild space–time is written in the spherical coordinates as
[6]
where
ϕ = −
GMe/
r is the Newtonian gravitation potential with Earth’s mass
Me. With the coordinate transformation
φ →
Ωet +
φ, in which
Ωe is the angular speed of the Earth’s rotation, we can directly obtain the metric in the rotating frame as
Selecting the coordinate origin on the surface of the Earth with the transformation
r →
Re +
r, we can rewrite the metric of the local laboratory frame in the rectangular coordinates as
Here,
Re is the radius of the Earth and

is the gravity acceleration on the surface of the Earth. The linear speed of the Earth’s rotation is
Ve =
Ωe ×
Re. Based on Eqs. (
6) and (
9), the Lagrangian for a torsion pendulum in the local laboratory frame can be expressed as
where d
m denotes the infinitesimal mass and the
z direction is assumed to be along the plumb line with
g = −
gez. Since the suspension point of the torsion fiber is fixedly connected with the laboratory, the local laboratory frame can actually be regarded as the suspension point frame.
When we only consider the angle deflection θ, the position vector of the infinitesimal mass dm can be expressed as (x, y, z) = (Lp cos θ, Lp sin θ, −l) in the suspension point frame, in which Lp is the distance between an arbitrary point on the torsion pendulum and the center of the pendulum, and l is the length of the torsion fiber. However, in real experiments, due to the vibrational noise from seismicity or control systems, the torsion pendulum has a pendulum motion in addition to the horizontal rotation. Therefore, the position vector of dm will change. For simplicity, we set δφx(t) and δφy(t) as the angular displacements of the fiber from the vertical position in y and x directions, respectively. With the coordinate transform shown below
the position vector of d
m turns out to be
By substituting Eq. (
12) into Eq. (
10), we can obtain a Lagrangian function related to
θ,
δφx, and
δφy. Here, we set
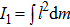
as the moment of inertia of the torsion pendulum related to the pendulum motion and
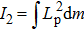
as the moment of inertia of the torsion pendulum related to the rotation motion. Because the torsion fiber goes through the center of the pendulum and the pendulum is symmetric, the relations of ∫
Lp d
m = 0, ∫
xyd
m = 0, ∫
zxd
m = 0, and ∫
zyd
m = 0 are satisfied. As the angular displacements
δ φx(
t) and
δφy(
t) are very small, the approximation of sin
δφ ≈
δφ and cos
δφ ≈ 1 is reasonable. Therefore, the final simplified Lagrangian in the suspension point frame can be expressed as
in which only the first order terms of
δφx(
t) and
δφy(
t) are kept.
4. Evaluating the influence of the Earth’s rotationBased on the Lagrangian expression in Eq. (13), the motion equations of torsion pendulum’s rotation and pendulum motion can be respectively obtained. For the rotation of the torsion pendulum, the following equation is satisfied:
Substituting Eq. (
13) into Eq. (
14), we can further obtain
Due to the high stability of the Earth’s rotation,
Ω changes very little with time and affects the motion of the torsion pendulum mainly by coupling itself with the pendulum motion. Here, we set
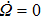
, equation (
15) can be rewritten as
For the pendulum motion of the torsion pendulum, it can be decomposed into separate
x and
y components. For the
y component, we can obtain
and further derive the motion equation as
Similarly, the motion equation of the
x component is
Since the pendulum motion has little effect on the rotation of the torsion pendulum, only the main effects need to be considered, while some small coupling effects can be ignored. Thus, equations (
18) and (
19) can be approximated as
and the corresponding solutions to Eqs. (
20) and (
21) can be derived as
where
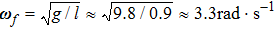
denotes the oscillation frequency,
Ax (
Ay) and
φx (
φy) are the amplitude and initial phase, respectively.
Substituting Eqs. (22) and (23) into Eq. (16), we can obtain
and the corresponding general solution is
with the angular frequency

. This solution describes the free oscillation of the torsion pendulum. By substituting Eq. (
25) into the right side of Eq. (
24), it can be rewritten as
To simply make the order estimate, equation (
26) can be approximately expressed as
Assume that the form of the particular solution of Eq. (
27) is
θf(
t) =
Af sin(
ωft +
φy) with
which includes the perturbation brought by the Earth’s rotation. Eventually, the complete solution of Eq. (
24) is approximate to
Based on the typical parameters
A0 ∼ 3 mrad,
Ay ∼ 1 mrad,
I2 ∼ 4.8 × 10
−5 kg ·m
2,
Ωx ≈
Ωy ∼ 7.2 × 10
−5 rad · s
−1,
k ∼ 1.1 × 10
−8 N · m · rad
−1,
Cg ∼ 0.9 kg
2 · m
−1,
G ∼ 6.674 × 10
−11 m
3 · kg
−1 · s
−2, we can obtain
Af ≈ −2.4 × 10
−8 rad.
To extract the effective oscillation frequency of the motion described by Eq. (29), the correlation method[16–18] is usually used, which determines the frequency by comparing the measured signal with a strictly sinusoidal reference signal. Here, we generate two groups of data with sampling time of 840 s by MATLAB. One group is a strictly sinusoidal signal with amplitude A0 and period τ0 = 2π/ω0 ≈ 420 s. The other group is based on the first group, and additionally includes a perturbative signal with amplitude Af and period τf = 2π/ωf ≈ 1.9 s. With the correlation method, the period difference between the first and second data groups is Δ τ ≈ −6.5 × 10−9 s. The contribution to the uncertainty of G measurement with the time-of-swing method can be expressed as
Taking
τn −
τf ≈ 1.5 s, we can obtain Δ
G/
G ≈ −6.1 × 10
−3 ppm. This means that if the amplitude of the pendulum motion of the torsion pendulum is controlled at the level of milliradian, the uncertainty brought by the Earth’s rotation will be far less than 1 ppm.
5. SummaryAt present, the highest precision of G value is given by the angular acceleration method and the time-of-swing method. However, there are still some systematic errors that need detailed modeling and analysis, such as the Earth’s rotation effect. For the angular acceleration method, the relevant analysis of the Earth’s rotation effect has been completed, but in experiments of the time-of-swing method, we only roughly estimated the magnitude of the effect before. Therefore, we present a more complete analysis and assessment process of this effect here. We derive the motion equations of the torsion pendulum with the Lagrangian expression in the general relativistic frame. After the calculation and simulation, we find that the main effect of the Earth’s rotation contributes to G measurement by coupling itself with the pendulum motion of the torsion pendulum. This effect is far less than 1 ppm, as long as we control the amplitude of the pendulum motion at the level of milliradian. The model we put forward is applicable to other similar gravitational experiments with torsion pendulum, in which the influence of the Earth’s rotation may need to be carefully considered.