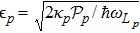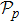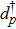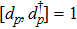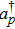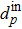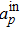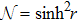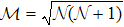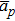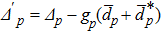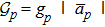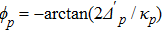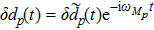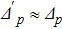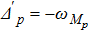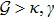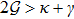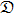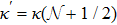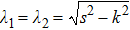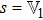Quantifying non-classical correlations under thermal effects in a double cavity optomechanical system
1. IntroductionEntanglement[1–3] is a fundamental feature of quantum mechanics, which plays a crucial role in different applications of quantum information processing, such as quantum teleportation,[4] superdense coding,[5] telecloning,[6] and quantum cryptography.[7] In optomechanical systems, entanglement is due to the interaction between the movable mirror and the radiation field via the radiation pressure.[8–10] Recently, several studies have been conducted to investigate entanglement and quantum correlations in optomechanical systems.[11–17] But the entanglement is very fragile under the thermal effect when the quantum system interacts with its environment; it is a decoherence phenomenon.[18] Moreover, in optomechanical systems, it has been found that the entanglement disappears rapidly under the effect of certain parameters; it is the entanglement sudden death (ESD) phenomenon.[19] This phenomenon occurs when the entangled multipartite quantum system is placed in Markovian environments.[20–24]
In this paper, we use a system consisting of two spatially separated Fabry–Pérot cavities, each cavity having a movable end-mirror (as shown in Fig. 1). Our objective is to study the quantum correlations between mirror 1–mirror 2 and optical 1–optical 2 modes in this system, by making use of the rotating wave approximation. Thus, after derivations of the steady state of the mechanical and optical modes of two-mode continuous variables Gaussian states, we will analyze Gaussian intrinsic entanglement and Gaussian geometric discord in terms of Hellinger distance to quantify quantum correlations, while as the purity to quantify the mixedness between mechanical and optical modes.
The rest of the present article is organized as follows. In Section 2, we describe the model and the system under investigations, we also give the expression of the Hamiltonian and the quantum nonlinear Langevin equations (QLEs) for the mechanical and optical modes. In Section 3, we linearize the QLEs and derive the quantum equations that govern the dynamics of the system. In Section 4, in Gaussian state of continuous variables we calculate the covariance matrix of the system in the steady state. Then, we study the Gaussian intrinsic entanglement[25] to measure the quantum correlations between mechanical and optical modes, and the purity to measure the mixedness[25,26] (Section 5). Finally, we use also the Gaussian geometric discord in terms of the Hellinger distance to characterize the quantum correlations beyond the entanglement between mechanical and optical modes[28] (Section 6). Conclusions close the paper.
2. ModelWe consider two Fabry–Pérot cavities composed of a fixed mirror (spatially transmitting) and a movable mirror Mp (p = 1, 2) (perfectly reflecting). The mass and the frequency of the pth movable mirror are respectively mp and ωMp. As illustrated in Fig. 1, the cavities are coupled to a common two-mode squeezed light from the output of the parametric down conversion, and are pumped by coherent laser field which is coupled to the movable mirror M1 (M2) via radiation pressure with the coupling rate
 ,[10] where Lp is the pth cavity length.
,[10] where Lp is the pth cavity length.
The system Hamiltonian in frame rotating with ωLp is given by[12]
where
ωap is the
pth cavity frequency,
ϕp and
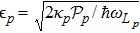
(
p = 1, 2) are respectively the phase and the input coherent field.
κp is the cavity damping rate,
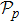
is the driving pump power,
ωLp is the frequency of the
pth input field. The mechanical modes are considered as quantum harmonic oscillators, with annihilation and creation operators
dp and
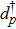
satisfying the commutation relations
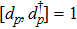
(
p = 1, 2).
ap and
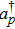
are the annihilation and creation operators of the
pth cavity mode, with

(
p = 1, 2).
Considering the Hamiltonian Eq. (1), the nonlinear quantum Langevin equations, describing the dynamics of the movable mirrors and optical modes are written by[29–31]
with
γp and
Δp =
ωLp −
ωap are respectively the mechanical damping rate and laser detuning (
p = 1, 2),
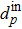
is the
pth noise operator describing the coupling between mechanical mode and its own environment and
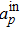
is the squeezed vacuum operator.
For a large value of the mechanical quality factor, it can be assumed that the mechanical baths are Markovian. The non-zero correlation function[32,33] is given by
where the thermal baths photons numbers in the
pth cavity is
with
kB being the Boltzmann constant.
The squeezed vacuum operators
 and
and
 have nonzero correlation properties[34]
have nonzero correlation properties[34]
where
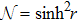
and
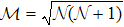
with
r being the squeezing parameter characterizing the squeezed light (we consider
ωM =
ωM1 =
ωM2).
3. Linearization of quantum Langevin equationsThe nonlinear quantum Langevin equations are in general non-solvable analytically. In this way, we use the scheme of linearization given in Ref. [35]
where
δ dp and
δ ap are the operators of fluctuations.

and
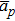
are respectively the mean values of the operators
dp and
ap. Considering Eqs. (
2) and (
3) in its steady state, one can obtain
where
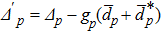
, is considered as the effective cavity detuning which depends on the displacement of the mirrors due to the radiation pressure force. Replacing

and

in Eqs. (
2) and (
3), thus
where
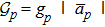
is the many-photon optomechanical coupling inside the
pth cavity,
ϕp is the arbitrary phase of
pth input laser
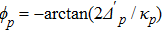
and

. Using the notations

,
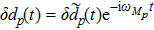
,

, and

, equations (
13) and (
14) became
Using the rotating wave approximation (RWA)
[10,36] (
i.e.,
ωMp ≫
κp with
p = 1, 2), the effective cavity detuning is reduced to
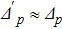
, and one can neglect the terms rotating at ± 2
ωMp. When the cavity is driven at the red sideband (
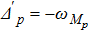
with
p = 1, 2), equations (
15) and (
16) become
4. Steady state covariance matrixThe linear quantum Langevin equations allow us to deduce the covariance matrix (CM) that describes the evolution of the steady state of the system, then to characterize purity, entanglement, and beyond entanglement between various modes by making use of different criteria and quantifiers of correlations.
For the sake of simplicity, we consider that the two coherent sources have identical strength, and the thermal baths of two mechanical mirrors are at the same temperature T1 = T2 = T (nth1 = nth2 = nth). Furthermore, m1 = m2 = m, ωr1 = ωr2 = ωr, ωM1 = ωM2 = ωM, κ1 = κ2 = κ, and γ1 = γ2 = γ.
To derive the explicit formula of the CM for continuous variables, we consider the EPR-type quadrature operators for the two subsystems
Equation (
17) becomes in terms of quadrature operators
[14]
with
Equations (
20)–(
23) are given in a compact matrix
[37]
with the following form of
where
Since all eigenvalues of the drift matrix

are negative (for
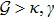
,
i.e.,
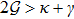
), the system under study is stable.
[38] The steady state of the system can be described by the covariance matrix whose form is

Then, the covariance matrix in steady state can be derived by considering Lyapunov equation, given by
[39,40]
with
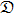
being the matrix of stationary noise correlations, whose elements are

the explicit expression of
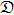
is
where

and
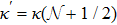
.
The covariance matrix in steady state is given by
For the two-mode symmetric squeezed thermal states, the covariance matrix for each subsystem (mirror 1–mirror 2 and optic 1–optic 2), can be derived considering the global covariance matrix Eq. (
30)
where
The opto-mechanical cooperativity
C is given by
[10]
The covariance matrices given in Eq. (
31) can also be written, for the two-mode symmetric squeezed thermal states, in the following compact matrix form
In Eq. (35), the index j represents a subsystem m1m2 (mirror 1 and mirror 2 modes) or o1o2 (optic 1 and optic 2 modes) and the matrix blocks
 and
and
 are the covariance matrix 2 × 2 respectively describing the single mode and the nonclassical correlations between the mechanical and optical modes. For subsystem m1m2 (
are the covariance matrix 2 × 2 respectively describing the single mode and the nonclassical correlations between the mechanical and optical modes. For subsystem m1m2 (
 and
and
 ) and for subsystem o1o2 (
) and for subsystem o1o2 (
 and
and
 ).
).
5. Gaussian intrinsic entanglement and purityIn this section, we will study the entanglement of the mechanical (m1 − m2) and optical (o1 − o2) modes in the symmetrical state by using the Gaussian intrinsic entanglement (GIE) and the purity. For the two-mode Gaussian states with continuous variables (CV), the Gaussian intrinsic entanglement is defined in Ref. [25]. For the symmetric squeezed thermal states with the covariance matrix given by (Eq. (35)), the Gaussian intrinsic entanglement is[25]
The condition of entanglement of the two modes is

, therefore if
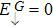
, the two modes are separable.
The purity of the two modes is given by[26,27]
where the index
j represents a subsystem
m1m2 (mirror 1 and mirror 2 modes) or
o1o2 (optic 1 and optic 2 modes). The purity
μ(j) is a witness of the mixedness of the Gaussian state with 0 ≤
μ(j) ≤ 1: the state of the two modes is mixed if
μ(j) < 1, and is pure if
μ(j) = 1.
The explicit expression of the purity for mechanical and optical modes is written respectively
If
r = 0 and
nth = 0, equations (
38) and (
39) lead to the maximum value of purity,
i.e.,
μm1m2 = 1 and
μo1o2 = 1.
We consider recent experimental parameters:[41] The laser frequency ωL/2π = 2.82 × 1014 Hz (λ = 1064 nm). The cavity length and frequency are respectively L = 25 mm and ωa/2π = 5.26 × 1014 Hz. The movable mirrors oscillate with frequency ωM/2π = 947 × 103 Hz, the mechanical damping rate γ/2π = 140 Hz and having the mass m = 145 ng.
In Fig. 2, we show the evolution of GIE of the mechanical modes (a) and optical modes (b) as a function of the thermal bath photons number nth for various values of the squeezing parameter r with a fixed values of C and γ/κ. When the GIE disappears, the two modes are not entangled. It is clear that, when the parameter r is equal to zero (r = 0), the two subsystems remain separable, as shown in Fig. 2. For a fixed value of photons number nth, the generation of the entanglement between, on the one hand, the mirror–mirror modes (see Fig. 2(a)) and, on the other hand, between the optic–optic modes (see Fig. 2(b)) improves with the increase of the parameter r (r > 0). This shows the dependence between the entanglement and the squeezing parameter r, as in Ref. [12]. In addition, figure 2 shows that for a given r (r > 0), the two optical modes (Fig. 2(b) remain entangled over a wider range of nth than the two mechanical modes (Fig. 2(a)). We can also see that movable mirrors and optical modes become separable when the photons number is around nth ≥ 4 and nth ≥ 6.5 respectively. Since the number of photons is directly related to the temperature, we can deduce that the optical modes remain entangled over a wider temperature range than the mechanical modes. This effect of temperature is the sign of decoherence.[18] Note also that as the photons number increases, the entanglement decreases quickly which means that the transfer of quantum correlations from two-mode light to the mechanical modes decreases monotonically. This phenomenon can also be explained by the concept of entanglement sudden death (ESD) as in Ref. [19].
In Figs. 2(c) and 2(d), we plot the evolution of the purity respectively of mirror–mirror modes and field–field modes as a function of thermal bath photon numbers nth for different values of r. It is clear that for the two subsystems, the purity reaches its maximum value (μm1m2 = 1, μo1o2 = 1) when r = 0 and nth = 0, according to Eqs. (38) and (39); then it decreases when the number of photons nth increases. We notice that the witness of mixedness increases with increasing thermal effect, and also with increasing squeezing parameter r, but the entanglement between the two mechanical modes and the entanglement between the two optical modes increase with increasing r. Indeed, for a fixed value of r > 0, when the purity increases also the entanglement increases as illustrate in Figs. 2(a)–2(c) and Figs. 2(b)–2(d). The comparison between Figs. 2(c) and 2(d) shows for r > 0 that the purity of optical modes remains superior for a wider range of temperature than mechanical modes, this may explain why optical modes remain entangled for a wider range of nth than mechanical modes as in Figs. 2(a) and 2(b). For example, when r = 0.5 and nth ≈ 2, we have GIE ≈ 0.06 for mechanical modes, and GIE ≈ 0.14 for optical modes. This finding can also be explained by the phenomenon of decoherence.
We remark also the importance of studying the effect of optomechanical cooperativity on the evolution of the entanglement between mechanical and optical modes. Figure 3(a) shows, for a fixed values of r and γ/κ, that there exists a minimum optomechanical cooperativity Cmin (i.e., C > Cmin) for which the mechanical modes (movable mirrors) start entangled if nth < 5 (i.e., the entanglement is vanishing if nth ≥ 5). We observe that the entanglement (GIE) between mechanical modes increases with the increase of C for a fixed value of nth, whereas for a given C, the GIE decreases with the increase of nth (see Fig. 3(a). Moreover, the value of Cmin, which corresponds to the birth of the entanglement of the mechanical modes, increases with the increase of nth (see Fig. 3(a)); this is explained by the effect of the decoherence on the entanglement of the two mobile mirrors.
Figure 3(b) shows that the optical modes are entangled even if nth ≥ 5, but mechanical modes are separable (see Fig. 3(a)). Moreover, when nth increases, we note that there exists a maximum value of the optomechanical cooperativity (C < Cmax) for which the optical modes are entangled. It is clear that the increase in the photons number nth causes the decrease of Cmax, for a given nth the GIE decreases with increasing optomechanical cooperativity, whereas when C is fixed, the GIE increases with decrease of nth.
Figures 3(c) and 3(d) illustrate the evolution of the purity of the mirror 1–mirror 2 and optic 1–optic 2 subsystems respectively with respect to the optomechanical cooperativity for different values of nth. For the two subsystems, the figures show that the purity decreases with the increase of nth, as it is clear from Eqs. (38) and (39), this due to the decoherence phenomenon. Remarkably, for mobile mirrors, purity increases very rapidly with C increases. In the case of optical modes, we observe a rapid decrease in purity for low values of C followed by a small variation and then it seems to stabilize for the large values of C (see Fig. 3(d)). Finally, following Fig. 3, we can conclude that the transfer of quantum correlations from the two-modes squeezed light to the mechanical modes has the effect of improving entanglement (when C > Cmin) and purity; but for both optical modes, the effect is reversed.
6. Gaussian discord with the Hellinger distanceIn this section, we will study the progress of Gaussian geometric discord in terms of Hellinger distance (GGD-Hd), in order to characterize the quantum correlations in bipartite Gaussian states,[28] using RWA. The two subsystems (mirror–mirror and optic–optic) are described by the covariance matrices, e.g., Eqs. (31) and (35), the explicit expression of GGD-Hd for the two-modes symmetric squeezed thermal states is given by[28]
where the index
j represents a subsystem
m1m2 (mirror 1 and mirror 2 modes) or
o1o2 (optic 1 and optic 2 modes) with
N1 = (
λ1 + 1/2)
2,
N2 = (
λ2 − 1/2)
2, and
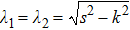
being the symplectic eigenvalues of the covariance matrices Eqs. (
31) and (
35), with
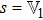
and

for mirror–mirror subsystem, and
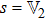
and

for optic–optic subsystem.
Figures 4(a) and 4(b) represent respectively the evolution of GGD-Hd of the two mirror–mirror and optical–optical subsystems as a function of the thermal bath photons numbers nth for different values of the squeezing parameter r with fixed values of C and γ/κ parameters. Indeed, when r = 0 the quantum correlations are not transferred between the two modes; this shows the strong relationship between squeezed light and quantum correlations. These figures show that GGD-Hd degrades with the increase of nth, but improves by increasing the parameter r. The comparison between Figs. 2(a) and Figs. 4(a) and 4(b) allows us to notice that when the two subsystems (mechanical or optical) are no longer entangled, GGD-Hd does not disappear. Therefore, GGD-Hd can quantify quantum correlations beyond entanglement. For example, when nth = 6 and r = 0.5, we have GIE=0 while GGD-Hd ≈ 0.08 for the two mechanical modes.
Figures 5(a) and 5(b) show respectively the effect of optomechanical cooperativity C on the GGD-Hd of the mirror–mirror and optical–optical subsystems for various values of the thermal bath photons numbers nth with fixed values of r and γ/κ. It is clear that, for the mechanical modes, the GGD-Hd decreases with the increase of nth, whereas it increases with the increase of C (Fig. 5(a)). For the optical modes, on the one hand, the GGD-Hd decreases with the increase of nth; this shows the effect of the thermal bath temperature which is proportional to the number of photons. On the other hand, the GGD-Hd exhibits a very rapid degradation with the increase of C, then seems to keep a stable value after a certain value of C which is less than 4 (Fig. 5(b). This behavior can be explained by the freezing phenomenon that has also been discussed in Ref. [42]. The comparison between Fig. 5 and Fig. 3 shows us that, when the mechanical and optical modes are separable, the GGD-Hd remains non-zero. Therefore, we can conclude that GGD-Hd is more robust than Gaussian intrinsic entanglement (GIE) under the thermal effect. In other words, GGD-Hd measures the total quantum correlations even if the two modes are not entangled under the thermal effect.
7. ConclusionIn summary, we have studied and compared entanglement, purity and Gaussian geometric discord in terms of Hellinger distance in an optomechanical system in the Gaussian state of continuous variables. The system consists of two spatially separated Fabry–Pérot cavities. Each cavity has a fixed mirror and a movable mirror, and is powered by two-mode squeezed light source and a coherent laser source. After giving the Hamiltonian expression and the non-linearized quantum Langevin equations, we derived the linearized quantum Langevin equations describing the dynamics of the system by considering the linearization scheme. Using the rotating wave approximation, we derived the explicit expression of the covariance matrix Eq. (30) of the Gaussian stationary state for the mechanical modes and the optical modes. We have used Gaussian intrinsic entanglement of two-mode continuous variables Gaussian states to quantify the amount of entanglement between mechanical and optical modes at strong coupling under thermal effect, which allowed us to highlight the phenomenon of sudden death entanglement under thermal effect. We have also shown the influence of various factors, such as temperature T, squeezing parameter r and optomechanical cooperativity C on entanglement generation. The analysis of purity as a witness of the mixing between the mechanical and optical modes, has shown that the purity is degraded under the thermal effect. The general nonclassical correlations were also quantified using Gaussian geometric discord in terms of Hellinger distance (GGD-Hd). We have found that GGD-Hd is more robust than entanglement for mechanical and optical modes under thermal effect. Indeed, this thermal effect lead to decoherence phenomenon, which remains a major challenge for information and quantum processing.