The basic interaction between a two-level atom and a classical light field was described by the Rabi model many years ago.^[1] Its fully quantized version in the rotating wave approximation (RWA) was introduced by Jaynes and Cummings later.^[2] The Jaynes–Cummings model can be easily solved due to the conserved excitations of the atom and the photonic number. It has been widely used in the quantum optics, because the basic physics explored in the Jaynes–Cummings model alone can be realized and observed in the earlier experiments due to the extremely weak coupling between the atom and the cavity, such as Rabi oscillations, collapses and revivals of quantum state populations, quadrature squeezing, and photon anti-bunching.^[3,4]

However, the situation has changed in the past decade. In many advanced solid devices, such as the circuit quantum electrodynamics (QED) system, two-dimensional electron gases, and trapped ions, the ultrastrong coupling^[5,6] and even deep strong coupling^[7,8] between the artificial atom and resonators have been accessed, and the RWA is demonstrated to be invalid.^[5] On the other hand, the two-level system appearing in the quantum Rabi model (QRM) and its variants is a qubit, which is the building block of quantum information technologies with the ultimate goal to realize quantum algorithms and quantum computations. Just motivated by the experimental advances and potential applications in quantum information technologies, the QRM in which the RWA is not made has attracted extensive attention.^[9–20] For more complete review, please refer to Refs. [21–23].

The QRM continues to inspire exciting developments in both experiments and theories recently. The anisotropic QRM^[24–26] was motivated by the recent experimental progress.^[27–29] It can be mapped onto the model describing a two-dimensional electron gas with Rashba (rotating wave coupling relevant) and Dresselhaus (counter rotating-wave coupling dependent) spin–orbit couplings subject to a perpendicular magnetic field.^[27] These couplings can be tuned by an applied electric and magnetic field, allowing the exploration of the whole parameter space of the model. This model can directly emerge in both cavity QED^[28] and circuit QED.^[29] For example, in Ref. [30], a realization of the anisotropic QRM based on resonant Raman transitions in an atom interacting with a high finesse optical cavity mode was proposed. On the other hand, Grimsmo and Parkins proposed a novel scheme by adding a nonlinear coupling term to the QRM Hamiltonian.^[31] This nonlinear coupling term has been discussed in the quantum optics literature under the name of dynamical Stark shift, a quantum version of the Bloch–Siegert shift, so it was later named the quantum Rabi–Stark model (RSM).^[32] This model also attracted much attention in recent years.^[33–35] Recently, the anisotropic Dicke model with the Stark coupling terms, which can be called as the anisotropic Dicke–Stark model, was demonstrated via cavity assisted Raman transitions in a configuration using counterpropagating laser beams.^[36] For one atom case, it is just the anisotropic RSM.

With the progress on various extensions of the QRM relevant experiments, different approaches have been developed to solve various QRMs.^[37] In this work, we will introduce a generical approach to solve the QRM and its several variants, such as the anisotropic QRM, RSM, and anisotropic RSM, in an unified way.

The paper is structured as follows. In Section 2, we propose and describe an unified analytic approach to the generalized QRM, which can be reduced to many different QRMs, using tunable coherent states. By solving the Schrödinger equation, all coefficients in the wave function can be related through the recurrence equations. The solutions for all eigenfunctions and eigenvalues of the model are obtained by locating zeros of a one-variable polynomial. The results are presented and discussed in Section 3, where the closed-form solutions for the ground-state and the first excited state are also given. The last section contains some concluding remarks.

The general QRM can be described as follows:

Fortunately, associated with this very general Hamiltonian is still the conserved parity , , where is the total excitation number. Π has two eigenvalues ± 1, depending on whether is even or odd. Due to this parity symmetry, we can study the general model (1) with the same scheme.

First, we employ the following transformation:

Next, we expand the eigenfunction as

By the Schrödinger equation, we have the same following equation for both up and down levels due to the conserved parity:

For any real physical systems, the wavefunction should be analytic and well defined, so the higher order coefficients should be vanishingly small. Strictly speaking, c_m→∞ → 0. But in the real calculation, one cannot set m to infinite as the numerical diagonalization proceeds in the truncated Hilbert space. Thus we need truncate the summation by setting c_mtr+1 = 0. c_{mtr + 1} is actually a polynomial in α, also in the energy E if using relation (6). The zero locations of Eq. (7) converge reasonably well with increasing truncated number m_tr. In principle, we can set infinite truncated number, but it is impossible to implement practically in the numerical calculations. All the coefficients can be obtained by this E-dependent polynomial equation, thus the eigenstates (4) can be also obtained. We actually can determine the solutions of the model with any desired accuracy by increasing truncated number m_tr. The solutions are demonstrated in the next section for arbitrary model parameters in various quantum Rabi models.

Most importantly, for arbitrary model parameters, the saturation calculation can be arrived at if m_tr is large enough, which results in exact solutions. It is very crucial to obtain the real roots of Eq. (7) for sufficient large truncation number m_tr. We plot a two-dimensional diagram c_{mtr + 1}(E). The schematic view of the solutions for the one-variable polynomial equation c_{mtr + 1}(E) with different model parameters in the most general model (1) are presented in Fig. 1. The real roots are just the intersection points of the curve and abscissa axis. The crossing points are just the solutions for eigenvalues E. Here the relative difference of the energy is less than 10⁻⁶ for all coupling strengths if m_tr is around 40. To confirm that all obtained eigenvalues are true ones of the model, we perform the numerical exact diagoanlizations (ED) in the Fock space. The ED results are indicated by the open circles. Excellent agreement is found for various parameters.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Schematic view of the solutions for the one-variable (E) polynomial Eq. (7) with (a) g = 0.5, U = 0.5, r = 0.5; (b) g = 1, U = 0.5, r = 0.5; (c) g = 0.5, U = 0.5, r = 2; and (d) g = 0.5, U = −0.5, r = 0.5. Even parity is denoted by blue and odd parity by red. The black circles are numerical ED solutions for the energy. Δ = 0.5.

By this method, we can further calculate the energy spectra for the general model (1) with arbitrary parameters. In Fig. 2, we plot the spectra for Δ = 0.5, U = 0.5, and r = 0.5. The numerical ED results are also exhibited with open circles. Both results are almost the same. Interestingly, the first two energy levels cross at one point. The level crossing just indicates the first-order quantum phase transition, because the first derivative of the lowest energy is discontinuous at this crossing point.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Energy spectra for Δ = 0.5, U = 0.5, r = 0.5 by both present approach (solid lines) and the numerical ED (black circles).

In the studies of the original simplest QRM, the analytical closed-form solution is very interesting and helpful.^[39,40] Now, in our unified framework, we can also present the closed-form solutions to this general model by terminating the summation in Eq. (7) at m_tr = 2, i.e., c₃ = 0, which yields

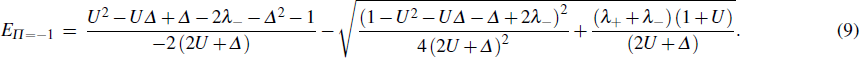Also considering the most complicate case, i.e., nonzero U and r ≠ 1, we plot the above two energies Eqs. (8) and (9) in Fig. 3 for Δ = 0.5, U = 0.5, r = 0.1. The first 4 energy levels from the exact solutions are also displayed for comparison. The level crossing of the first two exact energy levels also appears in the corresponding closed-form solutions. Although deviating from the true crossing point, the qualitative feature is still captured in the simple closed-form study. One may note that the present closed-form solution is only a second-order approximation, but the essential feature of the model is still included. It may highlight that in the present ansatz (4), only a few terms in the expansion can dominate the true one.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. A few low levels for Δ = 0.5, U = 0.5, r = 0.1 by both the closed form (filled circles) and the exact solutions by zeros of Eq. (7) (solid lines). Level crossing appears for both cases.

In the recent experiments, many solid-state devices can be operated in the ultra-strong cavity–cavity coupling regime, i.e., g < 0.2. From Fig. 3, one may see that the closed-form solutions are very close to the true ones up to the ultra-strong coupling regime. This situation becomes even better for the ground-state energy. In Fig. 4, we plot the ground state energy up to g = 0.5 by Eq. (8). An excellent agreement in wider coupling regime is obviously exhibited.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Comparisons of the ground-state energies by the present closed form solution (filled circles) and the exact solutions by zeros of Eq. (7) (solid curves) for Δ = 0.5, U = 0.5, (a) r = 0.5 and (b) r = 2 (right).

We have proposed a unified approach to the quantum Rabi model and its several variants. A polynomial equation with a single variable is derived by tunable extended coherent states for the most general model, which is more complicate than the often studied models. The solutions to this polynomial equation recover exactly all eigenvalues and eigenfunctions of the models for arbitrary model parameters. Closed-form solutions are also given for the first two levels, which are very accurate up to the ultrastrong coupling regime. The first-order quantum phase transitions for some parameters are observed in the unified exact solutions, and also appear in the closed-form ones. Further physics phenomena in the presence of anisotropy and nonlinear Stark coupling will be explored within this unified scheme in the near future.

Finally, we like to point out that this unified method should be very helpful to analyze the experimental data in the recent circuit QED systems from the weak coupling, ultra-strong coupling, and deep-strong coupling regimes. For some experimental device, the underlying interactions information such as anisotropy and nonlinearity are not very clear, and thus the specified model is unknown in priori. By using the present universal approach, one can easily fit the experiential data to the theoretical results based on the generalized model where all possible interactions are taken into account, and finally detect the real interactions in the experiments.