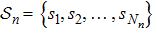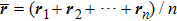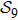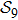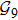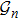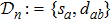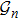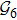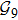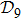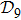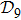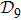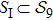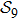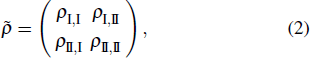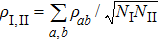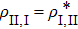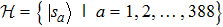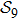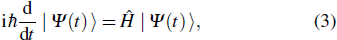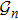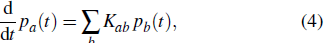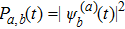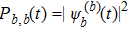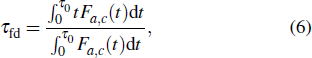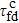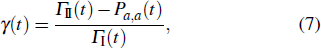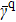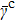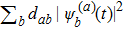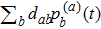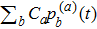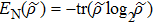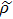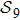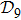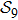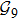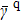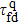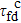1. IntroductionProtein folding problem has been an important topic in interdisciplinary field involving molecular biology, computer science, polymer physics as well as theoretical physics, etc. Levinthal noted early in 1967 that a much larger folding time is inevitable if proteins are folded by sequentially sampling of all possible conformations. It was widely assumed that a random conformational search does not occur in the folding process, for which various hypotheses with the help of a series of meta-stable intermediate states have been often proposed. There have been substantial theoretical models which are useful for understanding the essentials of the complex self-assembly reaction of protein folding with different simplifying assumptions, such as Ising-like model,[1,2] foldon-dependent protein folding model,[3] diffusion–collision model,[4,5] and nucleation-condensation mechanism.[6,7] However till now, this often brings in certain difficulties in connecting analytical theory to experimental results because some hypotheses can not be easily put into a practical experimental measurement since they often rely on various hypotheses.[8–12] As the approach of computing simulations introduced less hypotheses in comparison to those theoretical models, the atomistic simulations[13–15] have been also used to investigate the protein folding along with nowadays’ advances in computer science. All-atom computational method,[16] including physics-based and knowledge-based approaches, have provided useful insights on protein folding and design by building high-accuracy atomistic models of proteins. However, all those models are computationally costly for high-throughput folding studies and still need certain artificial hypotheses.
Recently, we proposed a quantum strategy[17] without making hypotheses to formulate protein folding as a quantum walk on a definite graph, in which we merely studied the model with six amino-acids as toy model. We know the shortest peptide chain in nature contains more than twenty amino-acid residues. Toward a genuine understanding, it is obligatory to study more complicate case with more residues. Here we consider the model with nine amino-acid residues and obtain that the folding time via our quantum approach is much shorter than the one obtained via classical random walk. Moreover, as the number of amino acid residues increases, the set of protein structures and the corresponding connection graph become more complicate, which drives us to introduce the projection method and several characteristic quantities. After calculating and analyzing those quantities, we find some new features on the folding pathways in addition to the fast protein-folding time. Our quantum approach that employs and combines the concepts of quantum walk and mean first-passage time not only reveals fast protein-folding time but also unveils the existence of quantum intelligence on the protein folding pathways, which is expected to open a significant new area of research.
2. Model descriptionIn the course-grained model the protein is considered as a chain of non-own intersecting unit[18–21] (usually referring an amino acid residue) of a given length on the two-dimensional square lattice. We indicated recently[17] that for a protein with n amino-acid residues, there will be totally Nn distinct lattice conformations that distinguish various protein intermediate structures, which provide us a point set with Nn objects. We call such a point set as structure set and denote it by
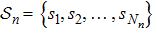 . The entire structure set includes various structures that may be an unfolded, partially folded or completely folded. To distinguish their difference, we introduce a concept of compactness of a structure,
. The entire structure set includes various structures that may be an unfolded, partially folded or completely folded. To distinguish their difference, we introduce a concept of compactness of a structure,
where the geometric center of the protein is located at
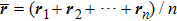
, and
rk refers to coordinates of the
k-th residues. Clearly, the compactness
Ca represents the average distance from each residues to its geometric center of a given structure
sa. We consider in this paper the case of
n = 9 and obtain
N9 = 388 through depth search algorithm (DSA). The 388 distinct structures that are unrelated by rotational, reflection or reverse-labeling symmetries
[20] were plotted (see supplementary material, Table S1). The straight-line structure is labeled lastly as
s388 for convenience since it is the farthest end of the depth-first algorithm search. We plot it together with the three most compact structures
s186,
s193, and
s236 in Fig.
1 as an illustration. For the structure set
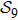
, the compactness of each structure is calculated (see supplementary material, Table S2). The largest value
C = 2.222 refers to the completely unfolded straight-line structure
s388, while the smallest value
C = 1.073 refers to the most compact structure
s186,
s193, and
s236.
In terms of the lattice model, we introduced previously the concept of one-step folding to describe the protein folding process.[17] The one-step folding is defined by one displacement of an amino acid in one of the lattice sites: two protein structures are connected via one-step folding if their chain conformations differ in one site only. For example, in Fig. 1, the structures s388 and s386 can be obtained by a one-step folding from s387, and so did s193 from s129. This enables us to establish certain connections between distinct objects in the structure set
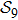 so that we have a connection graph
so that we have a connection graph
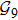 which is described by a 388 × 388 adjacency matrix Mat(Jab) that characterizes a classical random walk[22] on the connection graph.
which is described by a 388 × 388 adjacency matrix Mat(Jab) that characterizes a classical random walk[22] on the connection graph.
3. Distance space and its projectionsIf the aforementioned graph
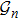 is completely connected, a distance between any two structures, saying sa and sb, is well defined. Then we will have a distance space
is completely connected, a distance between any two structures, saying sa and sb, is well defined. Then we will have a distance space
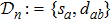 in which the magnitude of da b equals the number of steps of the shortest path connecting sa and sb in the graph
in which the magnitude of da b equals the number of steps of the shortest path connecting sa and sb in the graph
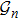 . There has been four line-crossings already when the 22-vertex graph
. There has been four line-crossings already when the 22-vertex graph
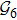 is plotted on a plane.[17] The
is plotted on a plane.[17] The
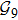 contains 388 vertices and appears very complicate if it is plotted on a plane. The largest distance in
contains 388 vertices and appears very complicate if it is plotted on a plane. The largest distance in
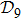 stretches between the completely unfolded straight-line structure s388 and the most compact structures s186 or s193, namely, d388,186 = d388,193 = 17. While the distance between the structure s388 and the other most compact structure s236 is no more the farthest, it is just d388,236 = 14.
stretches between the completely unfolded straight-line structure s388 and the most compact structures s186 or s193, namely, d388,186 = d388,193 = 17. While the distance between the structure s388 and the other most compact structure s236 is no more the farthest, it is just d388,236 = 14.
It will be very helpful to make a projection of the space
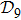 into an XY-plane. If mapping the s388 to the origin point (0,0) and either s186 or s193 to the farthest point at (17,0), we will have a set of points in the XY-plane where each point corresponds to one or several objects in the space
into an XY-plane. If mapping the s388 to the origin point (0,0) and either s186 or s193 to the farthest point at (17,0), we will have a set of points in the XY-plane where each point corresponds to one or several objects in the space
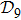 . Their concrete locations in the XY-plane are determined by the the distance away from (0,0) and that away from (17,0), respectively. The former represents the distance away from the straight-line structure s388 and the later represents that away from either s186 or s193 in the distance space
. Their concrete locations in the XY-plane are determined by the the distance away from (0,0) and that away from (17,0), respectively. The former represents the distance away from the straight-line structure s388 and the later represents that away from either s186 or s193 in the distance space
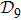 .
.
The color scatter diagram shown in Fig. 2 exhibits the aforementioned projection of
 on XY-plane, in which the color of each dot measures the degeneracy that is defined as the number of distinct structures mapping to the same point in the XY-plane. The degeneracy of each dot in the above figure and the concrete structures contained in the original images are all listed in supplementary material (see Table S3). Those points lain on the X axis in between (0,0) and (17,0) are the images of the objects referring to the shortest path leaving away from the initial structure s388 and approaching to a most compact structure. Those objects on the shortest path together with the one mapped to (17,0) constitute a subset
on XY-plane, in which the color of each dot measures the degeneracy that is defined as the number of distinct structures mapping to the same point in the XY-plane. The degeneracy of each dot in the above figure and the concrete structures contained in the original images are all listed in supplementary material (see Table S3). Those points lain on the X axis in between (0,0) and (17,0) are the images of the objects referring to the shortest path leaving away from the initial structure s388 and approaching to a most compact structure. Those objects on the shortest path together with the one mapped to (17,0) constitute a subset
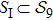 . If let Sii denote the set constituted by the other objects, then the structure set
. If let Sii denote the set constituted by the other objects, then the structure set
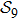 can be partitioned into two subsets Si and Sii, namely,
can be partitioned into two subsets Si and Sii, namely,
 .
.
The density matrix ρ(t) describing quantum dynamics is of 388 × 388 that is too large to manifest some useful information. The above projection picture helps us to properly reduce the large density matrix to a 2 × 2 one to extract certain useful information, namely,
where
ρI, I = ∑
aρaa,
ρII, II = ∑
bρbb,
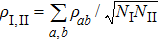
and
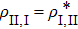
with
a ∈
SI,
b ∈
SII and
NI,
NII the total numbers of the objects in the corresponding subsets. Here the large density matrix stands for
ρ(
t) = |
Ψ(
t)〉〈
Ψ(
t)|.
4. On the time evolutionLetting |sa〉 denote the state of a protein structure in the shape of the a-th lattice conformation, we will have a quantum Hamiltonian in a 388-dimensional Hilbert space
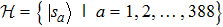 , namely,
, namely,
 where Jab refers to the connections between different objects in the structure set
where Jab refers to the connections between different objects in the structure set
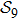 , i.e., Jab is not zero if the a-th protein structure can be transited into the b-th one by a one-step folding while vanishes otherwise. With these physics picture one can investigate quantum walk[23–25] on the aforementioned graph, which gives a quantum mechanical understanding of the protein folding, i.e., the process by which proteins achieve their native structure. As the time evolution is governed by the Schrödinger equation
, i.e., Jab is not zero if the a-th protein structure can be transited into the b-th one by a one-step folding while vanishes otherwise. With these physics picture one can investigate quantum walk[23–25] on the aforementioned graph, which gives a quantum mechanical understanding of the protein folding, i.e., the process by which proteins achieve their native structure. As the time evolution is governed by the Schrödinger equation
in which

, and the expansion coefficients
ψa(
t) can be solved numerically at least. In our numerical calculation, we set
ℏ and
J to be unity and take the time step as Δ
t = 0.02. For the initial condition, |
Ψ(0) = |
s388〉, we solve the first-order differential equation (
3) by means of Runge–Kutta method and obtain the magnitude of
ψa(
t) at any later time,
t =
j⋅Δ
t with
j = 1,2,…
In order to compare with the protein folding problem in the classical literature, i.e., a random conformation search process, let us revisit the classical random walk. The continuous-time classical random walk[24] on a graph
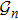 is described by the time evolution of the probability distribution p(t) that obeys the equation of motion
is described by the time evolution of the probability distribution p(t) that obeys the equation of motion
where
Kab =
Tab –
δab with
Tab being the probability-transition matrix. In the conventional classical random walk, the probability-transition matrix is determined by the adjacency matrix of an undirected graph, namely,
Tab =
Jab/deg(
b) where deg(
b) = ∑
cJcb represents the degree of vertex-
b in the graph.
It is widely believed that the native structure of a protein possesses the lowest free energy.[26] This can be interpreted by the hydrophobic force that drives the protein to fold into a compact structure with as many hydrophobic residues inside as possible.[19] How fast does a protein initially in a straight-line structure fold into the most compact structure and what is the main behavior during the folding process will be important issues to study.
5. Folding time and folding pathwayWe let Pa,b(t) denote the probability of a state being the basis state |b〉 at time t if starting from the state |a〉 at initial time t = 0. Quantum mechanically,
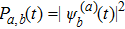 as long as we solved the Schrödinger equation (3) in terms of the initial condition |Ψ(0)〉 = |sa〉. Here the superscripts are introduced to distinguish the solution from different initial conditions. As we know, the first-passage probability Fa,b(t) from a state |sa〉 to another state |sb〉 after t time obeys the known convolution relation[27–31]
as long as we solved the Schrödinger equation (3) in terms of the initial condition |Ψ(0)〉 = |sa〉. Here the superscripts are introduced to distinguish the solution from different initial conditions. As we know, the first-passage probability Fa,b(t) from a state |sa〉 to another state |sb〉 after t time obeys the known convolution relation[27–31]
where
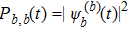
arises from the solution of Eq. (
3) from another initial condition |
Ψ(0)〉 = |
sb〉. In the classical case,
Pa,b and
Pb,b refer to the
pb(
t) solved from Eq. (
4), respectively, with initial conditions
pc(0) =
δac and
pc(0) =
δbc.
As protein folding is the process that proteins achieve their native structures, the folding time is the case that the starting state is chosen as |s388〉 and the target states are the most compact states |sc〉. For example, they are |s186〉, |s193〉 for n = 9 as aforementioned. With the help of the first-passage probability solved from Eq. (5), we can calculate the folding time by the formula
where
τ0 represents the time period when the first-passage probability vanishes
Fa,b(
τ0) = 0 firstly.
[17] Here
a = 388 and
c = 186 or 193. We know in a previous work that the quantum folding is faster than the classical folding with about four to six times even for the simplest model of 4 residues and it is faster than the classical folding with almost ten to hundred times or more for
n = 6.
[17] Here we calculate the folding time for
n = 9 that is given in Table
1. We can see that the quantum folding time
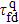
is much shorter than the classical folding time
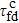
, and their difference becomes more significant in the case of
n = 9 in comparison to that of
n = 6.
Table 1.
Table 1.
 | Table 1. The probability ratio and the folding time. . |
In order to explore whether there are any intelligence hidden behind in choosing the protein-folding pathway, we compare the total probability on the shortest path and the other path by a probability ratio γ to demonstrate how it changes relatively after it leaves the initial state, namely,
where Γ
σ(
t) = ∑
b ∈ SσPa,b(
t) with
σ = I, II. Our result is plotted in Fig.
3, we can see that the magnitude of
γ changes from 0 to 1 monotonously during a short period of time for both quantum and classical cases. This implies that the probability on the shortest path is more favorable after leaving the initial state for it is on the denominator of
γ. In order to rule out the ambiguity on the time scales about classical and quantum literature, we evaluate a mean ratio,

and show them in Table
1. The mean ratio in quantum case
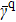
is smaller than that in classical case
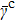
. This implies that the probability distribution is more aggregated on the shortest path in quantum case.
6. More on folding behaviorAlthough the random walk reflects a stochastic process, it is characterized by the probability distribution defined on all the distinct structures that can always give us intuitive information if we calculate some weighted average of the entire system. We can attain the time dependence of mean distance away from any structure sa by calculating
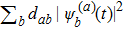 . We can also observe the time evolution of the mean compactness
. We can also observe the time evolution of the mean compactness
 . In classical case, the mean distance and mean compactness is evaluated by
. In classical case, the mean distance and mean compactness is evaluated by
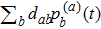 and
and
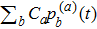 respectively. Our calculation of those two average quantities are given in Fig. 4. We can see that the mean distance of leaving away from the initial straight-line structure s388 increases much more rapidly in the quantum folding process than in classical case (see Fig. 4(a)). Correspondingly, the mean distance approaching to the most compact structures s186 and s193 decreases more rapidly (see Figs. 4(b) and 4(c)) in the quantum folding process than in classical one. Additionally, the average of compactness also decreases more rapidly in the quantum folding process than in class case (see Fig. 4(d)), thus the protein classically shrinks slower and it quantum mechanically shrinks faster.
respectively. Our calculation of those two average quantities are given in Fig. 4. We can see that the mean distance of leaving away from the initial straight-line structure s388 increases much more rapidly in the quantum folding process than in classical case (see Fig. 4(a)). Correspondingly, the mean distance approaching to the most compact structures s186 and s193 decreases more rapidly (see Figs. 4(b) and 4(c)) in the quantum folding process than in classical one. Additionally, the average of compactness also decreases more rapidly in the quantum folding process than in class case (see Fig. 4(d)), thus the protein classically shrinks slower and it quantum mechanically shrinks faster.
As we know, quantum mechanically, the off-diagonal elements of a density matrix reflect certain quantum coherent properties, but our discussion till now have not yet involve it directly. The partition of entire structure set into subset by considering the concept of shortest path helps us to have a 2 × 2 density matrix. It is then worthwhile to calculate von Neumann entropy[32]
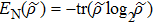 . We also calculated the Shannon entropy[33] ES = −pI log2pI – pII log2pII for the classical result to compare. Here pI = ∑a ∈ SIpa and pII = ∑b ∈ SIIpb. The aforementioned 2 × 2 density matrix
. We also calculated the Shannon entropy[33] ES = −pI log2pI – pII log2pII for the classical result to compare. Here pI = ∑a ∈ SIpa and pII = ∑b ∈ SIIpb. The aforementioned 2 × 2 density matrix
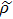 can also define a quantity called the degree of coherence[34,35]
can also define a quantity called the degree of coherence[34,35]
 , which is related to various quantum coherence phenomena, such as Rabi oscillation, self-trapping, etc. After making some calculus, one can find that the degree of coherence and the von Neumann entropy reach the extreme value at the same time, precisely, η(t) takes minimal value when EN(t) takes its maximum.
, which is related to various quantum coherence phenomena, such as Rabi oscillation, self-trapping, etc. After making some calculus, one can find that the degree of coherence and the von Neumann entropy reach the extreme value at the same time, precisely, η(t) takes minimal value when EN(t) takes its maximum.
The time dependence of both von Neumann and Shannon entropies are plotted in Fig. 5. We can see that both entropies change from 0 monotonously to a maximal value and then varies. The maximal von Neumann entropy means the quantum state is in a completely mixed state (the degree of coherence vanishes), while a maximal Shannon entropy implies the maximal information uncertainty. In our present problem, the population (or probability summation in classical case) on the shortest path is dominated during the time before the entropy reaches the maximal value. Clearly, such a period in quantum case is longer than in classical case. This illustrates from another angle of view that quantum folding process posses more intelligence in protein folding pathway.
7. SummaryIn the above, we studied the protein folding problem on the base of the quantum approach we proposed recently[17] by considering the model of protein chain with nine amino-acid residues. We have shown that the protein folding can be modelled as a quantum walk on the graph
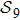 of 388 vertices. As such a graph appears complicate if it were plotted on a plane, we introduced the concept of distance space
of 388 vertices. As such a graph appears complicate if it were plotted on a plane, we introduced the concept of distance space
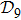 and its projections on a XY-plane by choosing two farthest structures (one is the completely unfolded straight-line structure and the other is a most compact structure) as reference-base points. According to our scheme,[17] we obtained the protein folding time by making use of the first-passage probability. In order to attain more understandings on the folding behavior, we introduced two characteristic quantities, one is called compactness of protein structure and the other is called probability ratio involving shortest path. The introduction of the concept of shortest path help us to reduce the 388 × 388 large density matrix to a 2 × 2 density matrix. Then we can conveniently evaluate the von Neumann entropy, etc. We also calculated the Shannon entropy on the base of classical random walk approach to compare. Our results not only confirmed the fast quantum folding time[17] but also unveiled that a quantum intelligence hidden behind in the choosing protein folding pathways.
and its projections on a XY-plane by choosing two farthest structures (one is the completely unfolded straight-line structure and the other is a most compact structure) as reference-base points. According to our scheme,[17] we obtained the protein folding time by making use of the first-passage probability. In order to attain more understandings on the folding behavior, we introduced two characteristic quantities, one is called compactness of protein structure and the other is called probability ratio involving shortest path. The introduction of the concept of shortest path help us to reduce the 388 × 388 large density matrix to a 2 × 2 density matrix. Then we can conveniently evaluate the von Neumann entropy, etc. We also calculated the Shannon entropy on the base of classical random walk approach to compare. Our results not only confirmed the fast quantum folding time[17] but also unveiled that a quantum intelligence hidden behind in the choosing protein folding pathways.