† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11764039, 11847304, 11865014, 11475027, 11305132, and 11274255), the Natural Science Foundation of Gansu Province, China (Grant No. 17JR5RA076), and the Scientific Research Project of Gansu Higher Education Department, China (Grant No. 2016A-005).
We analytically and numerically discuss the stability and dynamics of neutral atoms in a two-dimensional optical lattice subjected to an additional harmonic trap potential and artificial magnetic field. The harmonic trap potential plays a key role in modifying the equilibrium state properties of the system and stabilizing the cyclotron orbits of the condensate. Meanwhile, the presence of the harmonic trap potential and lattice potential results in rich cyclotron dynamics of the condensate. The coupling effects of lattice potential, artificial magnetic field, and harmonic trap potential lead to single periodic, multi-periodic or quasi-periodic cyclotron orbits of the condensate. So we can control the cyclotron dynamics of neutral atoms in optical lattice by manipulating the strength of harmonic confinement, artificial magnetic field, and initial conditions. Our results provide a direct theoretical evidence for the cyclotron dynamics of neutral atoms in optical lattices exposed to the artificial gauge magnetic field and harmonic trap potential.
Ultracold atoms in optical lattices provide an ideal platform for studying a lot of fundamental phenomena of many-body physics.[1,2] The technology of laser cooling and neutral atoms trapping[3] has been greatly developed, which provides the conditions for the realization of Bose–Einstein condensation (BEC). The dynamical properties of ultracold atoms trapped in optical lattices[4] subjected to an artificial gauge field have been attracted much attention in experimental and theoretical research.[5–9] Recently, the ways to synthesize optically magnetic field for neutral atoms resulting from the Berry’s phase[10] have attracted great interests. When a neutral atom moves in a predesigned laser field, its center-of-mass motion is similar to that of an electron subjected to a Lorentz force in a magnetic field.[9] There are many ways to generate an artificial gauge field, such as laser-assisted hopping,[5,11] Raman coupling,[10,12] and lattice shaking.[13] The realization of the artificial magnetic field in optical lattices[14–18] leads to the observation of many new phenomena, for instance, the creation of vortices,[10,19,20] the coherent transportation of atoms,[21–25] the nonlinear waves,[26,27] the phase transitions,[28,29] and the oscillations of atomic clouds.[30,31] The creation of vortices without rotating the atomic cloud indicates the existence of the artificial gauge magnetic field. The significant effects of artificial magnetic field on the dynamics of neutral atoms make this research very popular. Particularly, the artificial gauge magnetic field induces cyclotron dynamics of neutral atoms in optical lattices, which is well observed experimentally.[5–8] The cyclotron dynamics of the neutral atom is another direct evidence for the generation of the artificial magnetic field and plays a key role in manipulating the coherent transportation of the atoms in optical lattices. Thus it would be significant to study how to control the cyclotron dynamics of neutral atoms in optical lattices theoretically.[32]
Ultracold atoms trapped in optical lattices subjected to an artificial gauge magnetic field provide an ideal platform for manipulating cyclotron dynamics of neutral atoms in a controllable way.[7,8] However, neutral atoms in pure optical lattices under the action of the artificial magnetic field will experience the instability problems.[33] In order to improve the stability, it is important to study the effect of the additional external confinement potential on the dynamics of the neutral atoms in optical lattices. The modifications of the topological states caused by the smooth confinement potential in optical lattice were discussed.[34–39] However, the dynamics of neutral atoms in optical lattices under the influence of an artificial gauge field and a confinement potential is not clear. Therefore, it would be important to consider the dynamics and stability of neutral atoms in optical lattice with additional artificial magnetic field and confinement potential.
The aim of the present work is to study the stability and dynamics of ultracold atoms in two-dimensional (2D) square optical lattices under the action of an artificial gauge magnetic field and harmonic trap potential theoretically and numerically. The coupling effects of lattice potential, artificial magnetic field, and harmonic trap potential result in rich and complex cyclotron dynamics phenomena of neutral atoms. Without the harmonic trap potential, there are multiple equilibrium points in the system and the cyclotron center of the condensate is also multiple. The distribution of the (un)stable equilibrium points in lattice plane changes periodically with the lattice site. However, after the addition of the harmonic trap potential, only one equilibrium point exists in the system. The harmonic trap potential plays an important role in modifying the equilibrium state properties and stabilizing the cyclotron orbit of the condensate in magnetized optical lattice. In addition, the existence of the lattice potential complicates the cyclotron orbits of the condensate. Due to the coupling effects of lattice potential, artificial magnetic field, and harmonic trap potential, the cyclotron orbit of the condensate can be single periodic, multiply periodic or quasi-periodic. Hence, we can manipulate the cyclotron dynamics of neutral atoms in optical lattice by controlling the strength of artificial gauge magnetic field, harmonic trap potential, and initial conditions.
We focus on the influence of an artificial gauge field and an additional external potential on the dynamics of neutral atoms in 2D square optical lattices in (x,y) plane. The optical lattice is so deep that we can work in the tight-binding limit.[40] The vector potential corresponding to the effect of the uniform artificial gauge field under the Landau gauge is 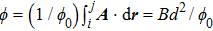
where 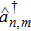
Here, the asterisk denotes the conjugation. The first term of Eq. (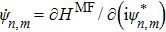
Obviously, the artificial magnetic field applied in the optical lattice is asymmetric in the x and y directions.
We focus on discussing the coupling effects of the optical lattice, artificial magnetic field, and harmonic trap potential on the cyclotron dynamics of the center of the mass of the condensate by using the variational method. Here we consider the case of noninteracting atoms (i.e., with g/J = 0, which can be tuned by the Feshbach technique).[41] Thus, the Gaussian ansatz is appropriate and valid
which defines a Gaussian distribution of the atoms centered at the position (ξx(t), ξy(t)) with width (Rx(t),Ry(t)) and momenta (px(t), py(t)) at a given time t. This Gaussian trial wave function is simple and convenient for obtaining the cyclotron dynamics of the center of the mass of the condensate with the variational analysis. For simplicity, we assume the widths of the condensate unchanged with time, i.e., Rx(t) ≡ Rx(0) and Ry(t) ≡ Ry(0). Taking the advantage of Euler–Lagrangian equations, where Lagrangian 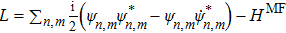

and the variational equations
Equation (
When the harmonic trap potential is absent, i.e., γ = 0, we can get the following equilibrium points from Eqs. (
where l,k = 0,±1,±2,… When px0, py0, and ϕ are fixed, equation (
At this case, the analytical results of cyclotron orbit of the condensate can also be obtained:
where H0MF is the initial Hamiltonian of the system. We can find that the cyclotron orbit of the condensate given by Eq. (
When the harmonic trap potential is present, i.e., γ ≠ 0, the system (2) only has one stable equilibrium point, i.e., 
Combining Eqs. (
Obviously, both the artificial magnetic field and harmonic confinement affect the cyclotron motion of the condensate. The coupling effects of the lattice potential, artificial magnetic field, and harmonic trap potential make the cyclotron dynamics of the condensate quite complexity. Although we cannot find the analytic result, we can obtain the asymptotical cyclotron orbit of the condensate under the condition of small cyclotron radius. By linearizing Eqs. (
Setting 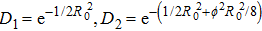
where
Here, parameters D1 and D2 express the effect of the optical lattice. When D1 = D2 = 1, the lattice is absent. We can see that the cyclotron dynamics of the condensate is affected not only by the artificial magnetic field ϕ and harmonic trapping γ but also by the lattice potential and initial conditions. On the other hand, the presence of the additional harmonic trap potential changes the equilibrium state properties and modifies the cyclotron dynamics of the system.
To understand the modification of the harmonic trap potential on equilibrium state and its stability of the system, figures 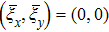
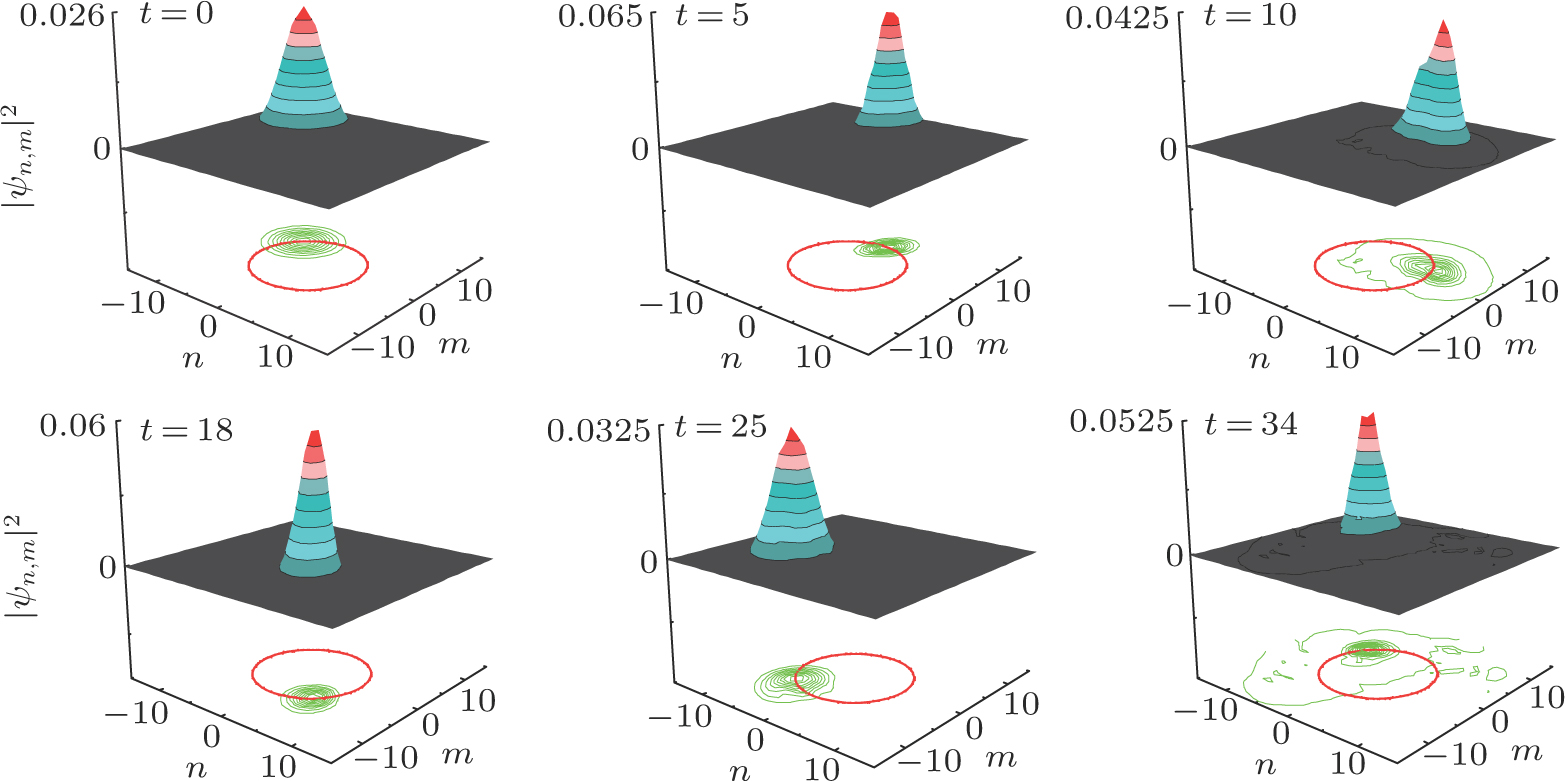
When ϕ = 0.189 and γ = 0, (ξx0,ξy0) = (50,50) is an unstable equilibrium point under the action of lattice potential. At this case, the cyclotron orbit is unstable and the condensate expand disorderly with time (see the first row in Fig.
In order to have a deeper understanding of the cyclotron dynamics of the condensate, the two eigenmodes of ω1 and ω2 given by Eq. (
In order to more clearly understand the dependence of cyclotron dynamics on the coupling effects of the lattice potential, artificial magnetic field, and harmonic trap potential, we obtain many kinds of cyclotron orbits from Eqs. (
We can obtain single periodic orbit by setting c1 = c2 = 0 or c3 = c4 = 0 according to the asymptotical solution of Eqs. (
So, the orbit of the condensate can be written as
It shows that when γ and ϕ satisfy Eqs. (
To confirm the above theoretical predictions, as an example, we set the initial position (ξx0,ξy0) = (−5,5) and the initial momenta (px0, py0) = (0.5,1.0). Then we can obtain the corresponding strength of the harmonic trapping γ = 0.018 and artificial magnetic field ϕ = 0.094 from Eqs. (
If ω1/ω2 is a rational number, the cyclotron trajectory given by Eqs. (
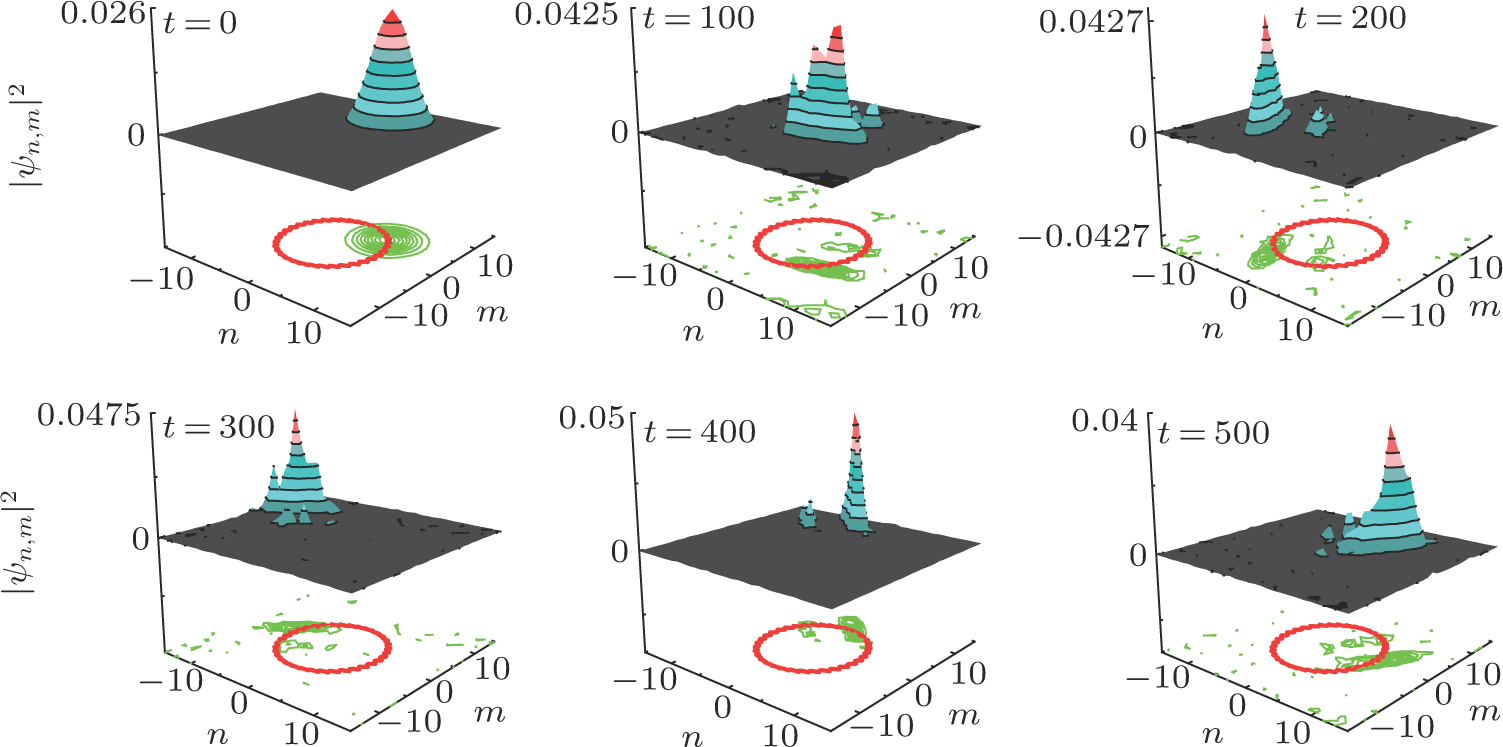
where 1/Q means a rational number. So given the initial conditions and the magnetic field intensity, we can get the corresponding strength of the harmonic trap potential which makes ω1/ω2 = 1/Q a rational number. We plot the orbits given by Eqs. (
We also plot the temporal evolution and the contour plot of the wave packet in Fig.
If ω1/ω2 is an irrational number, the asymptotical cyclotron orbit of the condensate given by Eqs. (
In summary, we considered the effects of the artificial magnetic field and harmonic trap potential on the cyclotron dynamics of the neutral atoms in optical lattices. Rich and complex dynamics phenomena of neutral atoms in optical lattices are predicted under the coupling effects of lattice potential, artificial magnetic field, and harmonic confinement.
In the absence of the harmonic trap potential, there are multiple equilibrium points with different stability characters in the system and the stability of the system depends on the stability of the equilibrium point. In this case, the stable orbit of the condensate is only the single periodic orbit, which circling around the stable equilibrium point. However, the existence of the harmonic trap potential significantly modifies the equilibrium state properties and the stability of the condensate in optical lattice exposed to the artificial magnetic field. There is only one equilibrium point in the system, so the cyclotron center is only one as well. The asymptotical cyclotron dynamics of the condensate is the composition of the two different eigenmodes. The lattice potential significantly modifies the high-frequency mode, which causes rich dynamics phenomena of the condensate. Therefore, the coupling effects of lattice potential, artificial magnetic field, and harmonic trap potential lead to single periodic, multi-periodic or quasi-periodic cyclotron orbit of neutral atoms. In these cases, although the condensate may not keep its initial Gaussian shape as time goes on, the mass center of the condensate follows the theoretically predicted trajectory. So we can manipulate the cyclotron dynamics of neutral atoms in optical lattice by adjusting the strength of the artificial magnetic field, harmonic trap potential, and initial conditions.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] |