We use the form of hierarchical geographical network model reported in Ref. [20] to describe the transportation system in the real world. There are H layers with N₁ nodes in the first layer and node number expansion rate q between layers h and h − 1, thus the number of nodes in layer h is

The total number of agents in the system is M = A × N, where A is the average number of agents in a node. Each agent i is assigned to an initial node n, corresponding to its permanent residence in the real world, and agent i is called a resident of its initial node n. Probability of i assigned to n is proportional to , where h_n is the layer of n, and 0 < ω < 1 is to adjust the difference of average number of residents in a node between each layer. Agents are all located in their initial nodes before the moving process begins.

We consider that agents move globally with preference for layers and memory of initial nodes. A highly developed traffic system enables human to arrive in any corner of the world in one day, thus in the model, agents can visit any node in the network in a time step, which is different from most metapopulation network models where agents can only visit neighbor nodes of their current nodes in a time step. Human moving process is modeled as follows.

(i) Travel For each agent i located in its initial node n, at each time step, i leaves n with probability p_travel and enters node m along the shortest path with the probability

(ii) Wait When i arrives in node m, it will be assigned a waiting time t_w that is drawn from the heavy-tailed distribution , where α is an adjustable parameter governing the distribution of t_w and T_max is the maximum waiting time in a non-initial node. Here i stays in m for t_w time steps then goes to step (iii).

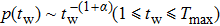
(iii) Return or drift After waiting for t_w time steps in node m, i will return back to its initial node n along the shortest path with probability p_return, then starts again from step (i) at the next time step; otherwise, it will drift to another non-initial node j that is chosen according to Eq. (3), followed by step (ii).

Local infection process is described by the SIR model. At each time step, each agent contacts with k other agents in the same node. In addition, each agent that moves at the time step additionally contacts with k other agents in each intermediate node it passed between the origin node and the destination node during the move. When a susceptible agent contacts with an infected agent, the susceptible one gets infected with probability p_SI if the contact occurs neither in the intermediate nodes of the infected agent nor in the intermediate nodes of the susceptible agent, or with probability r × p_SI otherwise. At the same time, infected agents are removed with probability p_IR at each time step.

At the first time step, agents are all susceptible and located in their initial nodes. In order to make the population distribution stable in each layer, we let agents move under the model rules for 1000 time steps before the infection is introduced. We set the initial infection in layer h_init by randomly choosing an agent in h_init as the initial infector, i.e., infection source. We fix the model parameters as default parameter settings in all the following discussions, unless a given parameter value is differently specified: the network parameters S = 100, H = 4, N₁ = 6, q = 6, thus N = 1554; the human moving parameters A = 100, M = 155400, ω = 0.5, p_travel = 0.005, p_return = 0.8, μ = 0, β = α = 0.6 and T_max = 365; and the infection parameters k = 5, p_SI = 0.06, p_IR = 0.1, r = 0 and h_init = 1.

According to Ref. [21], the Euclidean distance of human moving obeys power-law distribution p(r) ∼ r^{−(1 + b)}, which can also be generated in our model. Figure 2(a) shows the power-law exponent b decreases from 1.55 to 0.42, as μ decreases from 2.0 to −2.0, indicating that moving to high layers increases the frequency of long-range moves. The proportion of global moves between different subnetworks decreases as μ increases, as shown in Fig. 2(b), because of the shorter distance between high-layer nodes and other subnetworks. In addition, we compare the number of intermediate nodes in a move of the residents of each layer. Figure 2(c) shows that residents of low layers pass more intermediate nodes in a move than residents of high layers. In addition, moving to high layers further reduces the number of intermediate nodes for high-layer residents, while it increases the number of intermediate nodes for low-layer residents.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Human moving process in a hierarchical geographical network with H = 3 and q = 2. Larger nodes represent higher-layer settlements.

Fig. 2.

Figure Option ViewDownloadNew Window

Fig. 2. Impact of preference for layers on human moving behavior. (a) The move-length distribution of agents under different μ, where the move length is measured by the Euclidean distance. (b) The proportion of global moves as a function of μ. (c) The number of intermediate nodes in a move of residents of each layer under different μ. All the results are averaged by 100 runs, each of which lasts for 103 time steps.

Spreading velocity and propagation scale are two important concerns in epidemic spreading dynamics. In the SIR model, the spreading velocity is often measured by the peak timing of new infected cases, and the propagation scale is measured by the proportion of the removed agents at the end of the infection, i.e., at the time when there are no infected agents left. However, propagation scale is not appropriate to measure the spreading risk, due to the different spreading behaviors, including surging or ultra-slow increase of the infected agents, and rapid extinction or ultra-slow decrease of them. For example, slowly increasing the number of infected agents with long time scale leads to large propagation scale, but the risk is low due to the sufficient time to deploy mitigation measures. Therefore, more attention should be paid to the spreading velocity in the case-growing phase of the spreading process. The peak timing of new infected cases is also not enough to measure the spreading velocity, because it only expresses the time it takes for an infection to reach its maximum value of new infected cases, i.e., the peak value, and the peak value is also an important index of the spreading velocity. In this study we focus on large-scale spreading of epidemics, i.e., global spreading, in which infected nodes exist in every subnetwork. In this case, the peak value and peak timing of new cases, respectively represented as C(τ) and τ, are used to measure the velocity of the spreading, with larger C(τ) and smaller τ corresponding to larger spreading velocity.

We first investigate the influence of h_init and μ on the spreading velocity in each layer. Figures 3(a) and 3(b) display C(τ) and τ of each layer respectively in the case of different μ and h_init. Infection always spreads faster in high layers than in low layers regardless of the preference for layers and location of infection source, while moving to low layers and early infection in low layers reduce the difference of spreading velocity between high and low layers. This is because of the aggregation of agents in the relatively small number of high-layer nodes. Then we study the influence of h_init and μ on the overall spreading velocity. Figure 3(c) shows that the infection spreads faster when h_init is smaller, and smaller μ further accelerates epidemic spreading, indicating that early infection in the high-layer nodes and moving to the high-layer nodes both accelerate epidemic spreading. A node is infected when there are infected residents in it. Therefore, a node gets infected by two means: resident-induced infection and visitor-induced infection. Resident-induced infection is caused by the return of infected residents that get infected in other non-initial nodes, and visitor-induced infection is caused by residents of the node that get infected by infected visitors entering the node. Due to the faster infection in high-layer nodes, moving to the high-layer nodes increases the proportion of visitor-induced infection of high-layer nodes, while it reduces the proportion of visitor-induced infection of low-layer nodes, as shown in Fig. 3(d). This result also indicates that larger proportion of nodes in high layers get infected by visitor-induced infection than in low layers, and resident-induced infection is the main form of node infection. Here h_init has little influence on the proportion of visitor-induced infection of each layer, as shown in Fig. 3(e). In the real world, moving behavior differences exist among residents of different layers due to the position in the traffic system and social relations. In this paper we mainly discuss two aspects of layer-related moving behavior differences that may have influence on epidemic spreading, i.e., travel frequency and preference for layers.

Fig. 3.

Figure Option ViewDownloadNew Window

Fig. 3. Epidemic spreading under different preference for layers and location of infection source. (a) C(τ) and τ of agents in each layer under different μ. (b) C(τ) and τ of agents in each layer under different hinit. (c) Overall C(τ) and τ versus hinit under different μ. (d) Proportion of visitor-induced infection of nodes in each layer under different μ. (e) Proportion of visitor-induced infection of nodes in each layer under different hinit. Each point is generated from 500 simulations of global infection.

To represent the differences of travel frequency between residents of each layer, we first set the average travel probability of all the agents as p_travel, thus the average number of agents travelling from their initial nodes at each time step is M_init (t) × p_travel, where M_init (t) is the total number of agents that are in their initial nodes at time t. Next, we consider that the number of travelling agents of layer h is proportional to h^λ at each time step, where λ governs the degree of the difference in the number of agents travelling from each layer. Thus the number of agents travelling from layer h is

Figure 4 exhibits C(τ) and τ versus λ. Figures 4(a) and 4(b) shows the case of h_init = 1 and h_init = 4, respectively, with no infection in the intermediate nodes considered, i.e., r = 0. Curves of C(τ) have different trends under different μ. C(τ) increases monotonically as λ increases from 0.0 to 4.0 in the case of μ = −2, while C(τ₀) increases first and then decreases in the case of μ = 2. This can be explained as follows. As residents in low layers are more dispersed, travel of low-layer residents is conducive to making residents of more nodes contact with each other. According to Figs. 3(a) and 3(b), agents in high layers get infected earlier. When μ is small, larger λ causes susceptible residents of more nodes to move up and contact with infected agents in high layers, thus increases resident-induced infection and C(τ₀) increases with λ. However, when μ is large, moving of low-layer residents no longer causes more resident-induced infection, due to more moves between low-layer nodes and contact between susceptible agents, which contribute little to the infection. At the same time, visitor-induced infection decreases as λ increases due to fewer infected agents travelling from high layers. Therefore, C(τ) first increases and soon decreases with λ in the case of μ = 2. Here τ increases monotonically as λ increases. According to Fig. 3(c), moving to the high-layer nodes accelerates the spreading process. When λ is small, there are relatively more agents travelling from high layers, leading to easier exchange of agents between subnetworks due to the shorter distance between high-layer nodes and other subnetworks, which accelerates the spreading process and reduces τ.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Peak value C(τ) and peak timing τ versus λ: (a) hinit = 1, r = 0, (b) hinit = 4, r = 0, (c) hinit = 1, μ = 2. The solid points represent C(τ) and hollow points represent τ. Each point is generated from 500 simulations of global infection.

Figure 4(c) shows the case that the infection in intermediate nodes is considered under h_init = 1 and μ = 2. Different from the case of r = 0, C(τ) increases monotonically with λ under r = 0.5 and r = 1. Larger r leads to larger difference in C(τ) and smaller difference in τ among cases of different λ. This is because low-layer residents go through more intermediate nodes than high-layer residents in a move, and when r ≠ 0, larger λ makes low-layer residents participate in the infection of more high-layer intermediate nodes, take the infection to other susceptible high-layer nodes, and bring the infection to their initial nodes, thus increases C(τ) and reduces τ.

To study the influence of the difference of preference for layers between residents of each layer on epidemic spreading, we first set λ = 0 to ensure that the number of agents moving from each layer is the same at each time step. We consider that residents of layer h has the same layer preference coefficient μ_h, and the layer preference coefficients of all layers are considered as an arithmetic progression, with the average value and tolerance Δμ. Thus the layer preference coefficient of residents of layer h is

Figures 5(a) and 5(b) shows the cases of h_init = 1 and h_init = 4, respectively, with r = 0. As can be seen from the figures, C(τ) decreases monotonically as Δμ increases. According to Figs. 3(a) and 3(b), infection spreads faster in high-layer nodes than in low-layer nodes. Cross-layer moving pattern enhances both visitor-induced infection by high-layer infected agents moving to low-layer susceptible nodes, and resident-induced infection by low-layer susceptible agents moving to high-layer infected nodes, thus increases C(τ). When r = 0, τ first decreases then increases as Δμ increases under h_init = 1, while τ increases monotonically under h_init = 4. This phenomenon can be explained as follows. Larger Δμ makes moves between high-layer nodes more frequent, and when the infection source is in the high layers, the infection can quickly spread to all the high-layer nodes, thus accelerates the spreading process and reduces τ. However, larger Δμ also makes residents of low-layer nodes, which accounts for most part of the total population, move to low-layer nodes, slowing down epidemic spreading. Therefore, when Δμ is too large, τ increases. On the other hand, when the infection source is in low-layer nodes, smaller Δμ instead facilitates the quick infection of high-layer nodes due to the cross-layer moving pattern. It also makes low-layer residents move to high-layer nodes, which further accelerates the spreading process. Thus τ increases monotonically as Δμ increases.

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Peak value C(τ) and peak timing τ versus Δμ: (a) hinit = 1, r = 0, (b) hinit = 4, r = 0, (c) hinit = 1. The solid points represent C(τ) and hollow points represent τ. Each point is generated from 500 simulations of global infection.

Figure 5(c) shows the case that infection in intermediate nodes is considered for h_init = 1. As r increases, the curve of τ gradually loses the decrease phase and increases monotonically. This is because larger r enhances the effects of cross-layer moving on the quick infection of high-layer nodes, by low-layer residents participating in the infection of more intermediate high-layer nodes when Δμ is small.

Border screening is a common strategy to prevent epidemics from spreading to other discrete settlements.^[39,40] However, effectiveness of border screening is still controversial. For example, confronted with the bursts of severe acute respiratory syndrome (SARS), Chinese government implemented entry screening policy which turned out to be very effective in preventing SARS from spreading to more cities. However, some research on travel restriction stated that travel restriction is highly ineffective in containing epidemics.^[10] In this paper, we propose two kinds of screening strategies respectively aiming at moves into or out of high-layer nodes, and moves of long distance.

As we know from the analysis above, moving to high-layer nodes is more conducive to reducing τ, and moving between high-layer and low-layer nodes is more conducive to increasing C(τ). Thus, strategy I is to weaken the spreading by shutting down high-layer nodes, i.e., preventing agents from moving into or out of high-layer nodes. On the other hand, global moves increase the contact range of agents and reduce the proportion of repeated contact between agents from different nodes, thus facilitates the spreading. Hence, to achieve better effects, preventing moves into or out of high-layer nodes should be together with preventing global moves, which is strategy II.

In order to ensure the feasibility, for strategy I we choose nodes in the top two layers to implement move screening in sequence from 1^st-layer nodes to 2^nd-layer nodes, and nodes are chosen randomly in the same layer. As N₁ = 6 and q = 6, the maximum number of target nodes is N₁ +N₂ = 42 and N_s = 6 represents move screening for 1^st-layer nodes. For strategy II, moves between subnetworks are also screened besides move screening for high-layer nodes. In addition, the probability that a chosen move is successfully screened is set as p_s = 0.8, which serves as the measure of success rate of the screening strategy. If a move is successfully screened when the agent is returning, then the return probability of the agent is 1 before the agent arrives in his initial node, representing that the trip out of the initial node is finished. Once the agent arrives in the initial node, his return probability is 0.8 again.

Figure 6 exhibits the results of strategy I and strategy II. Figure 6(a) shows the average proportion of moves screened out of all the moves in a time step before τ, which is represented as M_s, versus the number of target high-layer nodes N_s for strategy I and strategy II under μ = −2 and μ = 2. These two strategies screen more moves when μ is smaller. M_s increases monotonically as N_s increases, and the curves have larger slope when N_s ≤ N₁ = 6, especially under μ = −2. In addition, strategy II screens more moves than strategy I. The difference in M_s between the two strategies becomes smaller as N_s increases, and their difference is larger under μ = 2 than under μ = −2, indicating that screening for high-layer nodes can effectively screen out global moves when agents tend to move to high-layer nodes, but it is not effective when agents move to low layers. Figures 6(b) and 6(c) show C(τ) and τ versus N_s under different μ respectively for strategy I and strategy II. The curves of C(τ) and τ for strategy I have similar trends with them for strategy II. C(τ) decreases monotonically as N_s increases, especially sharply when N_s ≤ N₁ = 6, which is opposite to the trend of M_s versus N_s, while the curves of τ have similar trends with M_s versus N_s. Figures 6(d)–6(e) show the comparison of the effects between strategy I and strategy II respectively under μ = −2 and μ = 2. Strategy II has better effects in delaying epidemic spreading than Strategy I with the same value of N_s, and the difference of their effects increases under larger μ due to the enlargement of the difference of M_s according to Fig. 6(a).

Fig. 6.

Figure Option ViewDownloadNew Window

Fig. 6. Effects of strategy I and strategy II on delaying epidemic spreading under different μ. (a) Ms versus Ns for strategy I and strategy II under μ = −2 and μ = 2. (b) C(τ) and τ versus Ns for strategy I under μ = −2 and μ = 2. (c) C(τ) and τ versus Ns for strategy II under μ = −2 and μ = 2. (d) C(τ) and τ versus Ns for strategy I and strategy II under μ = −2. (e) C(τ) and τ versus Ns for strategy I and strategy II under μ = 2. Each point is generated from 500 simulations of global infection.

At the same time, we investigate on the screening strategy focusing on moves of long distance, which is strategy III. Here we set the distance threshold d_c, and moves with distance that is larger than d_c at the time step will be screened with p_s. Figure 7(a) exhibits M_s as a function of d_c under μ = −2 and μ = 2. M_s decreases monotonically, and the curves of M_s become flatter as d_c increases. M_s under μ = 2 decreases faster when d_c is small, while M_s under μ = −2 decreases faster when d_c is large. The shape of the curves of M_s versus d_c depends on the distribution of the moving distance under different μ. Figure 7(b) exhibits C(τ) and τ versus d_c under different μ. Similarly, as d_c increases, the curves of C(τ) and τ become flatter. It is noticeable that strategy III achieves better results in delaying epidemic spreading when μ is large, as τ under μ = 2 increases much faster than τ under μ = −2 as d_c decreases.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Effects of strategy III on delaying epidemic spreading under different μ. (a) Ms versus dc under μ = −2 and μ = 2. (b) C(τ) and τ versus dc under μ = −2 and μ = 2. Each point is generated from 500 simulations of global infection.

In the real world, M_s is an important factor to consider, and our goal is to minimize the value of M_s, at the same time meet the effects of delaying epidemic spreading. Expanding the screening range, i.e., increasing the number of target high-layer nodes for strategy I and strategy II, or reducing the value of d_c for strategy III, and increasing the success rate p_s, both can enhance the effects of delaying spreading, at the same time increase M_s. Thus, we discuss which method can achieve better results with the same M_s. Figure 8 shows the results of the three screening strategies with M_s in the case of different screening range and μ, and the value of M_s corresponds to different p_s in each case. Under the same value of M_s, smaller N_s with larger p_s has better effects than larger N_s with smaller p_s. Similarly, larger d_c with larger p_s has better effects than smaller d_c with smaller p_s for strategy III. Their difference is larger under μ = 2 than under μ = −2. This indicates that increasing the success rate of screening strategies for higher-layer nodes and longer-distance moves is more effective in delaying epidemic spreading than expanding screening range.

Fig. 8.

Figure Option ViewDownloadNew Window

Fig. 8. C(τ) and τ of the three strategies versus Ms with different screening range and ps from 0.1 to 0.9 under different μ. (a) Strategy I with Ns = 6,18,30,42 under μ = −2. (b) Strategy I with Ns = 6,18,30,42 under μ = 2. (c) Strategy II with Ns = 6,18,30,42 under μ = −2. (d) Strategy II with Ns = 6,18,30,42 under μ = 2. (e) Strategy III with dc = 5,20,35,50 under μ = −2. (f) Strategy III with dc = 5,20,35,50 under μ = 2. The solid points represent C(τ) and hollow points represent τ. Each point is generated from 500 simulations of global infection.

According to Fig. 2, agents moving to high-layer nodes increases the frequency of global moves and long-distance moves. Therefore, strategy I, strategy II and strategy III have similar effects in delaying epidemic spreading. However, they still have their own characteristics. Figures 9(a)–9(f) exhibit the comparison of the results of the three strategies with M_s in the case of different p_s and μ, and the value of M_s corresponds to different screening range in each case.

Fig. 9.

Figure Option ViewDownloadNew Window

Fig. 9. Comparison of the results of the three strategies with Ms in the case of different μ and ps: (a) μ = −2, ps = 0.4, (b) μ = 2, ps = 0.4, (c) μ = −2, ps = 0.6, (d) μ = 2, ps = 0.6, (e) μ = −2, ps = 0.8, (f) μ = 2, ps = 0.8. The value of Ms corresponds to different screening ranges in each case. The solid points represent C(τ) and hollow points represent τ. Each point is generated from 500 simulations of global infection.

Figures 9(a) and 9(b) show the comparison of the results respectively in the case of μ = −2 and μ = 2 under p_s = 0.4, and Figs. 9(c)–9(d) and Figs. 9(e)–9(f) show the comparison of the results in the case of different μ under p_s = 0.6 and p_s = 0.8. With the same value of M_s, the three strategies have similar effects on delaying epidemic spreading under μ = −2, because most global moves and long-distance moves start or end in high-layer nodes. However, when μ gets larger, larger proportion of global moves and long-distance moves are between low-layer nodes. Thus, the differences in the effects between the strategies become larger. Besides, larger μ also weakens the role of high-layer nodes in accelerating spreading, thus strategy II achieves smaller C(τ) and larger τ than strategy I with the same M_s.

Strategy III has the worst effects when M_s is small. This is because for strategy III, small M_s corresponds to large d_c, which means that moves of extremely long distance will be screened. In this case, moves between low-layer nodes account for a large proportion of the moves screened due to the long distance between them, which contribute less to the spreading velocity than moves into or out of high-layer nodes. As M_s increases, strategy III can screen global moves, even moves between high-layer and low-layer nodes within a subnetwork. At the same time, strategy III limits the moves of agents within the range of d_c, thus reduces the number of nodes whose agents can contact with each other. In contrast, strategy I does not reduce the move range of agents, and strategy II only limits moves within each subnetwork. Therefore, when M_s increases, strategy III reduces C(τ) and increases τ more obviously than strategies I and II. When M_s is large enough, strategy III has the best effects in reducing C(τ), while strategy I has the worst effects. However, strategy III does not outperform other strategies in increasing τ, because it is less effective than strategies I and II on screening moves into or out of high-layer nodes.