† Corresponding author. E-mail:
Project supported by the Science Fund from the Ministry of Science and Technology of China (Grant No. 2016YFA0301300) and the Fundamental Research Funds for the Central Universities, China.
We theoretically investigate the strong coupling in silver-molecular J-aggregates-silver structure sandwiched between two dielectric media by using classical methods. Fresnel equations are employed to solve our proposed structure. The results show that both the reflection and transmission spectra show a Rabi splitting-like line shape, revealing the strong coupling phenomenon. Furthermore, the radiative angle versus incident wavelength exhibits a Fano line shape. The strong coupling phenomenon can be well tuned by controlling the surface plasmon excitation, such as the incident angle and the thickness of the silver films. Our structure has potential applications in quantum networks, optical switches, and so on.
Strong interactions between cavities and quantum emitters open a new branch to manipulate light, which has much applications such as quantum networks,[1] single-atom lasers,[2] ultrafast single-photon switches,[3] and quantum information processing.[4–6] Recently, plasmonics cavities are widely used to realize strong coupling phenomenon with emitters in both theory and experiment at room temperature, which would lead the cavity and emitter mode hybridization and Rabi splitting.[7] There are lots of plasmonic cavities, such as single metallic nanoparticle/metallic nanoparticle array,[8–14] metallic gratings,[15,16] subwavelength hole arrays,[17] and the most popular structures of Krestchmann configurations.[18–22]
Kretschmann configuration is a fundamental structure to generate surface plasmon polaritons (SPPs).[23–26] Lots of Kretschmann configurations are widely used in nano-tweezers,[27] four-wave mixing,[28] and optical bistability.[29] The nonlinear effect of the lateral shift or Goos–Hänchen (GH) shift[30] is reported in Kretschmann configuration involving Kerr nonlinear medium.[29,31] If the molecular J-aggregates is sandwiched between two Kretschmann configurations instead of the dielectric medium, the relation between input and output turns to be very interesting and is a great point of exploration.
In this paper, we investigate the strong coupling in the structure based on two Kretschmann configurations involving molecular J-aggregates. The proposed structure is made up of a molecular J-aggregate layer sandwiched between two Kretschmann configurations. Incident light is injected from one Kretschmann configuration with an incident angle, and the output is detected in the other configuration. Fresnel equations are employed to solve our proposed structure. The parameters of molecular J-aggregates and Ag film are changed in order to show the impact on the output. Our structures have potential applications in quantum networks, optical switches, and so on.
The sketch of our calculation model is shown in Fig. 

 |
By solving the wave equation for the magnetic field at the interface between L2 and L3 (H3,down), we can obtain the relation between H3,down and the magnetic field at the interface between L3 and L4 (H3,up) as
 |
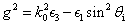
 |
 |
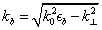
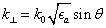
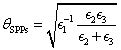
First, we calculate the structures without and with molecular J-aggregates. The thicknesses of Ag films and molecular J-aggregates are 20 nm and 50 nm, respectively. The incident angle is adopted as 40°. f is chosen as 0.01. We calculate the reflection and the transmission in the corresponding surfaces. The reflection (R), the transmission (T), and the output angle (θ0) versus the incident wavelength (λ) of the structures without and with molecular J-aggregates are shown in Fig.
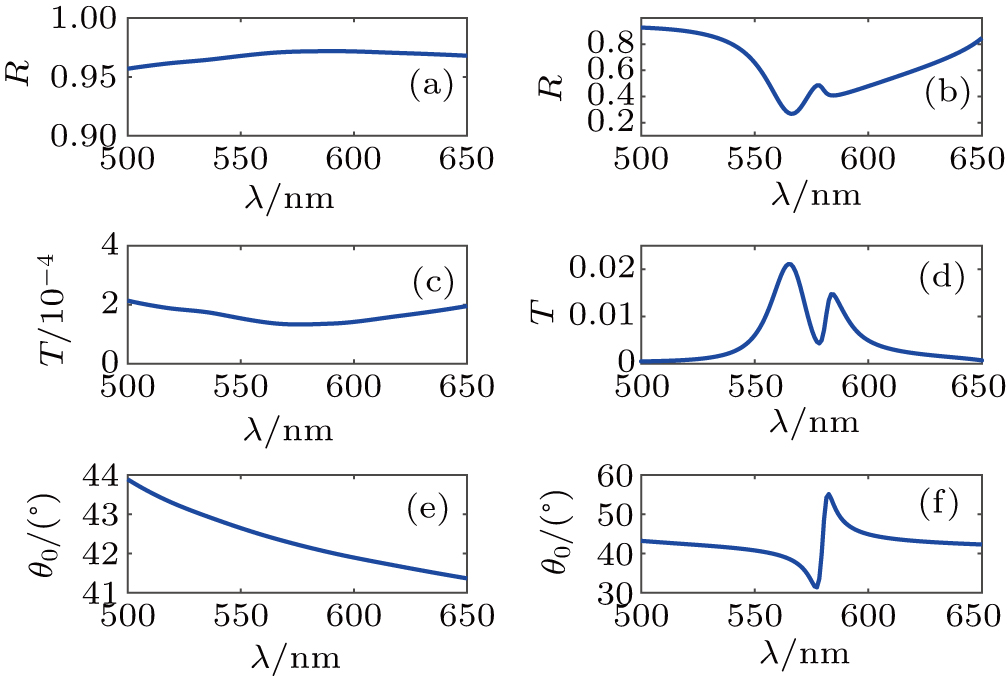 | Fig. 2. The reflection R [(a) and (b)], the transmission T [(c) and (d)] and the output angle θ0 [(e) and (f)] versus the incident wavelength λ without and with molecular J-aggregates. |
As shown in Figs.
The Fano line shape is induced by the interaction between SPPs and molecular J-aggregates. Light is injected from L1 onto L2 and is changed to SPPs which provides a dark mode, while molecular J-aggregates support a bright mode.[34–36] The interaction of the two modes makes the output angle versus the incident wavelength showing a Fano line shape with SPPs decoupling in the structure made up of L3, L4, and L5.
We also plot the real and the imaginary parts of r123 and r543 in Fig.
 | Fig. 3. The real and the imaginary parts of r123 and r543 with d1 = 20 nm, d2 = 50 nm, and θi = 40°, respectively. |
Furthermore, we use finite-difference time-domain (FDTD) method to calculate our proposed structure. We choose three wavelengths of 550 nm, 580 nm, and 583 nm, which covers the wavelengths around λx. The incident angle θi and the thickness of Ag film d1 are 40° and 20 nm. The thickness of molecular J-aggregates d2 is 50 nm. The indies of Ag and molecular J-aggregates are adopted as above. The gird is 0.5 nm. The output angle θ0, the transmission T, and the reflection R are listed in Table
| Table 1. Comparisons between FDTD and calculation. . |
Then, we change the incident angle θi to show the changes of the reflection spectrum R and the transmission T. The incident angles 38°, 40°, and 42° are adopted, R and T versus λ are shown in Fig.
 | Fig. 4. The reflection spectra (a) and the transmission spectra (b) with θi = 38°, 40°, and 42°, respectively. |
Rabi splitting in Kretschmann configuration is related with the interaction between SPPs and molecular J-aggregates. The intensities of SPPs for each wavelength are determined by the difference between the incident angle and θSPPs (Δθ = θi − θSPPs). If Δθ is less than 0 and θi is less than θSPPs in all wavelength regimes, there are few SPPs excited in Kretschmann configuration. θSPPs is changed from 30° to 55° in the wavelength regime from 500 nm to 650 nm. With the incident angle increasing from 38° to 42°, the wavelength regime for the best SPP excitation increases and there more and more SPPs interact with molecular J-aggregates. Hence, the Rabi splitting increases with the increase of the incident angle. With the increase of θi, much more energy of incident light is used to generate SPPs propagating along the interface between molecular J-aggregates and Ag film. Hence, the transmission decreases.
Then, we show the impact of f on the reflection spectra. The f is considered as 0.005, 0.01, and 0.015, and the results are shown in Fig.
 | Fig. 5. The reflection spectra (a) and the transmission spectra (b) with f = 0.005, 0.01, and 0.015, respectively. |
Finally, we change the thickness of Ag film to show how Rabi splitting changes. We adopt d1 = 15 nm, 20 nm, and 25 nm, and the reflection and the transmission spectra are shown in Fig.
 | Fig. 6. The reflection spectra (a) and the transmission spectra (b) with d1 = 15 nm, 20 nm, and 25 nm, respectively. |
As figure
In summary, we theoretically investigate the strong coupling in silver–molecular J-aggregates–silver structure sandwiched between two dielectric media by using Fresnel equations. Results show that both the reflection and the transmission spectra show the strong coupling phenomenon. The radiative angle versus the incident wavelength exhibits a Fano line shape around the resonant wavelength of molecular J-aggregates. The incident angle not only impacts on the intensity of the transmission, but also influences on the Rabi splitting. The oscillator strength and the thickness of Ag films are also used to tune the strong coupling. Our structure has potential applications in quantum networks, optical switches, and so on.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] |


