† Corresponding author. E-mail:
Project supported by the Fundamental Research for the Central Universities of China, the National Key Laboratory Project of Shock Wave and Detonation Physics of China, the Science and Technology Foundation of National Key Laboratory of Shock Wave and Detonation Physics of China, the National Key R&D Program of China (Grant No. 2017YFB0202303), the National Natural Science Foundation of China (Grant Nos. 51871094, 51871095, 51571088, NSFC-NSAF U1530151, and U1830138), the Natural Science Foundation of Hunan Province of China (Grant No. 2018JJ2036), and the Science Challenge Project of China (Grant No. TZ2016001).
Many of our previous studies have discussed the shock response of symmetrical grain boundaries in iron bicrystals. In this paper, the molecular dynamics simulation of an iron bicrystal containing Σ3 [110] asymmetry tilt grain boundary (ATGB) under shock-loading is performed. We find that the shock response of asymmetric grain boundaries is quite different from that of symmetric grain boundaries. Especially, our simulation proves that shock can induce migration of asymmetric grain boundary in iron. We also find that the shape and local structure of grain boundary (GB) would not be changed during shock-induced migration of Σ3 [110] ATGB, while the phase transformation near the GB could affect migration of GB. The most important discovery is that the shock-induced shear stress difference between two sides of GB is the key factor leading to GB migration. Our simulation involves a variety of piston velocities, and the migration of GB seems to be less sensitive to the piston velocity. Finally, the kinetics of GB migration at lattice level is discussed. Our work firstly reports the simulation of shock-induced grain boundary migration in iron. It is of great significance to the theory of GB migration and material engineering.
The migration of grain boundary (GB) is an important mechanism to change the internal structure of materials, so it is of great significance to properties of materials. Previous studies have shown that GBs would move under loading conditions, such as heating,[1] tensile,[2] shear,[3–6] surface deformation[7,8] and irradiation,[9] etc. Particularly, molecular dynamics simulations have indicated that some GBs can migrate automatically only in the thermal fluctuation under the free boundary condition.[4] It is very important to study the GB migration under these loading conditions to deepen our understanding of material science theory. The GB migration can be divided into two types: diffusion-based and shear-coupled ones.[2] Diffusion-based GB migration is achieved by atomic jump and driven by free energy difference.[10] Shear-coupled GB migration will not change the position of atoms dramatically and is driven by the shear stress along the GB surface.[11,12] In addition to the above loading conditions, GB migration also occurs under strong shock-loading conditions because strong shock will cause the instantaneous increases of pressure, shear stress and temperature, which can lead to GB migration. The studies of GB migration under shock-loading are still very little. Long et al.[13] found that shock-loading would induce migration of GBs in copper, and the GB migration occurs mainly in ATGBs. However, their works only involve the case that the shock direction is parallel to GBs. Moreover, the shock responses of face-centered cubic (FCC) metals (aluminum and copper) are quite different from those of body-centered cubic (BCC) metals (iron).[14–18] The mechanism of GB migration should be different for different lattice types. At present, we are still unclear about the mechanism of GB migration in iron under strong shock-loading.
Due to the significant role of iron in human industrialists and in the earth’s core, the behavior of iron under shock-loading has attracted a great deal of attention. A large number of experiments and simulations have been performed to investigate the shock response of iron.[19–26] A series of experiments[27,28] and simulations[10,29–31] have been carried out to study GB migration in iron. However, GB migration in iron under strong shock-loading has not been simulated. One of the reasons is that there is no suitable potential to simulate the plasticity of iron before phase transformation under shock for a long time. Therefore, it is impossible to perform the simulation related to the plasticity of iron under shock. Until recent years, Gunkelmann et al.[32] and our group (Wang et al.[15]) made a breakthrough in iron potential, respectively. Wang et al. developed the modified analytic embedded-atom method (MAEAM) potential, successfully simulated the plasticity before phase transition under shock, and greatly reduced the proportion of FCC atoms in phase transition products during BCC→hexagonal close-packed lattice (HCP) (a large number of FCC could not be observed in experimental[22]). After the breakthrough of potential, the simulation of iron under shock has more abundant phenomena than before. Another reason is that the stacking fault energy of iron is so high that GB migration cannot be observed easily in the simulation. Therefore, understanding of GB migration in iron under strong shock is almost absent.
Our group has carried out a series of works to study the interaction between GBs and phase transformation under shock-loading.[17,33–35] Gunkelmann et al. made a lot of achievements in studying the shock response of polycrystalline iron.[32,36,37] Unfortunately, the phenomenon of GB migration in iron under shock has never been observed in the simulation. Both symmetrical and asymmetrical grain boundaries have important effects on materials.[38–40] In our previous works, only shock response of iron bicrystal with symmetrical GBs is studied. What about asymmetric GBs? This work studys the shock response of asymmetric GBs, and shows the migration of Σ3 [110] ATGB under shock. The special shock response of GB migration is the reason why we choose Σ3 [110] ATGB. However, there are so many ATGBs, and it is difficult to summarize why only a part of ATGBs in iron under shock can migrate at present. Nevertheless, this paper firstly reports the simulation of GB migration in iron under shock-loading, which can fill in the blank of simulation and provide a reference for the experiment. Moreover, this study about the effect of GB migration on phase transition is an important supplement to our previous works about the interaction between GBs and phase transformation under shock-loading. Also, the mechanism of GB migration in iron under shock will attract a lot of attention because of the need of material dynamic damage research. Therefore, we discuss in detail the GB migration in iron bicrystal under shock-loading in this paper, and the interaction between GB migration and phase transformation under shock-loading are also revealed.
Non-equilibrium molecular dynamics (NEMD) simulations are performed through the LAMMPS[41] to investigate the migration of Σ3 [110] ATGB in iron bicrystal under shock. The potential used in this paper is MAEAM potential[15] developed by us recently, which has unique advantages in simulating the plastic behavior in iron under strong shock-loading. Figure
The GB migration in iron under shock has not been observed in previous simulations, where the GBs only provide nucleation sites for phase transformation, and even some GBs can be directly transformed into HCP lattices.[34,35] Due to the fact that the stacking fault energy of iron is very high, the phenomena of dislocation, stacking fault, slip and migration of GB are not easy relatively to be observed in the shock simulation. However, we recently discovered the migration of Σ3 [110] ATGB in iron bicrystal under shock.
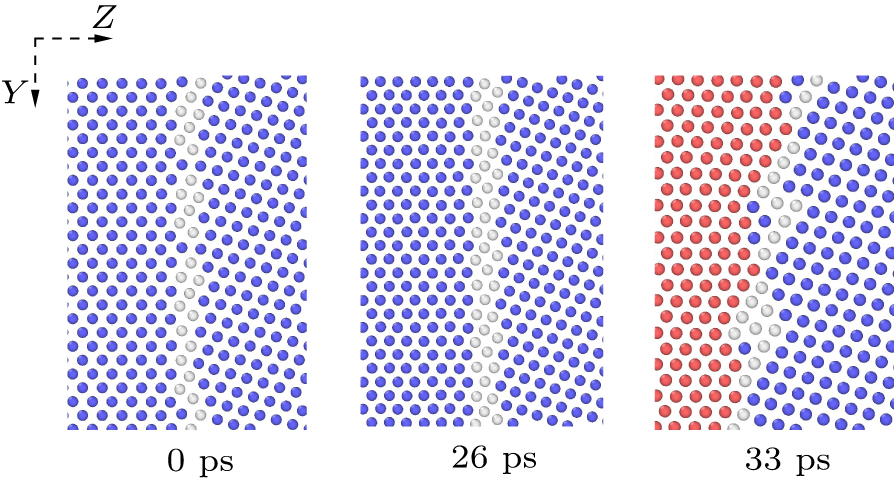
Phase transformation will be induced during GB migration when the piston velocity is 0.5 km/s. In order to study the interaction between GB migration and phase transition, the results with up = 0.5 km/s are analyzed emphatically. Figure
Although GB migration can be directly observed in morphology figures at different times, it can also be verified by means of tracing the GB at different times and the original GB atoms. The O in Fig.
Figure
As shown in Fig.
It was found that the migration of GB should be related to the shear stress on both sides of GB. Figure
 | Fig. 6. Evolution of the grain boundary migration velocity and difference between shear stress on both sides of grain boundary with up = 0.5 km/s. |
As mentioned above, the GB migration begins between about 23 and 24 ps when the piston velocity is 0.5 km/s. In Fig.
The study of dynamics can help to reveal the mechanism of GB migration. Figure 
Figure
 | Fig. 10. A group of atoms at about 10 nm to the right of the GB with up = 0.5 km/s at different times: (a) 0 ps, (b) 29.6 ps, (c) 29.8 ps, (d) 30.2 ps. The color code is the same as Fig. |
In order to investigate the mechanism of GB migration, we would track the movement of the selected atoms. Lattice constants are defined in the legend of Fig.
It has been mentioned above that GB migration is beneficial to phase transition, but it does not seem to have much effect on the threshold of phase transition. Figure
We have investigated the shock-induced migration of Σ3 [110] ATGB in α iron bicrystal via NEMD simulations. We observe the Σ3 [110] ATGB migration in iron bicrystal under shock and the migration type is shear-coupled. The shock-induced migration of Σ3 [110] ATGB would not change the shapes and local structures of GBs without the effect of phase transition. The migration of GBs seems to be less sensitive to the piston velocity, and the maximum velocities of GB migration with different piston velocities between 0.3 km/s and 0.6 km/s are nearly the same. The shock-induced shear stress difference between the two sides of GB is the key factor leading to GB migration, which can explain why migration of GBs occurs mainly in ATGBs. In particular, the dynamics of GB migration in iron is revealed firstly, and GB migration can help induce the phase transition. Also, it has been found that the phase transformation near the GB would change the shape and migration mechanism of GBs.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] |