† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11804085) and the Doctoral Foundation of Heze University, China (Grant No. XY18BS13).
We employ molecular dynamic simulation to investigate metabasin dynamics for supercooled polymer melt. We find that, in a small system, the α-relaxation process is composed of a few crossing events that the monomers hops from one metabasin to another. Each crossing event is very rapid and involves a democratic movement of many particles, whereas such collective motion is not string-like. Evaluation on the contributions of metabasin exploration and democratic movement shows that the structural relaxation is mostly governed by the latter. Our calculated results show that the metabasin–metabasin transitions are not the main reason of spatially dynamical heterogeneity. It is different from the binary Lennard–Jones mixture model in which the metabasin–metabasin transitions are relevant for the spatially dynamical heterogeneity.
The physical mechanism of glassy dynamics remains a central open problem in condensed matter physics.[1–4] One concerned topic is the nature of the motion of particles in the α-relaxation process at low temperature. This relaxation has been believed to proceed by means of cooperatively relaxing regions whose time scale and size grow considerably as the temperature is lowered.[1–8] In this relaxation process, the dynamics may vary by orders of magnitude from one region of the system to another.[5–7] This spatially dynamic heterogeneity (DH)[9–16] has been observed both in experiment and simulation. From the simulations of binary Lennard–Jones mixture (BLJM) systems[10] and direct observations in colloidal suspension experiments,[12,13] it is also found that the spatially DH is related to the cooperative motion, in which a small number of particles (a few percent) undergo a string-like collective motion with the displacements comparable to the distance between the neighboring particles.
One way to understand the α-relaxation dynamics is through the potential energy landscape (PEL).[1,17–19] The PEL is very rugged with the presence of many barriers and the dynamics becomes slow at low temperature. Within the concept of the inherent structures, the “metabasin” (MB) is defined as some minima which are locally connected and are not separated by significant barriers. The motion of the system in the PEL can roughly be decomposed into two types:[20,21] i) The system moves from one MB to another by crossing over barriers. This process is believed to correlate to the α-relaxation,[3] i.e., it is the elementary event of the α-relaxation.[21] ii) The system explores in an MB.
By molecular dynamic (MD) simulation, Appignanesi et al.[22] found that the α-relaxation of a small BLJM system (150 particles) corresponds to a small number of barrier hopping events from one MB to a neighboring one. Such hopping events are also realized by the collective motion of a significant fraction of particles which form relatively compact clusters. This movement is very different in nature from the string-like motion driven by a few fast moving particles in the context of spatially DH.[8,12,13] For a small BLJM system, the dynamics is also quite heterogeneous in time as the consequence of MB–MB transitions,[22,23] which leads to sharp bursts of mobility. This MB–MB transition that involves the collective motion of a significant fraction of particles has also been identified in the supercooled water simulation[24] and colloidal suspension experiment.[25] Polymer is a major glass-forming material that has been extensively studied.[26,27] The α-relaxation behavior of the polymer melt has been investigated in a wide range of temperatures.[28] The spatially correlated dynamics of the glass-forming polymer melt has also been studied by MD simulations.[29] But, whether the MB–MB transition exists in the polymer system or whether there are qualitative or quantitative differences in MB–MB transition between polymers and simple molecules is not clear. Hence, in this paper, we perform MD simulations on a coarse-grained polymer model to study the MB–MB transitions. Since we are interested in individual MB–MB transitions, one has to avoid the presence of several independent local rearranging regions, but this will occur in a large system and obscures the analysis of the individual event. So a small (100 monomers) system is employed.
The paper is organized as follows. Section
We adopt a bead-spring model of linear chains and each chain contains N = 10 monomers.[28–33] All monomers interact via a truncated and shifted Lennard–Jones (LJ) potential
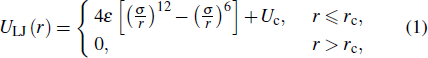 |
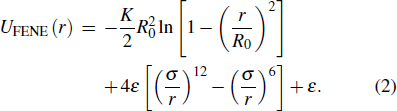 |
Using the above model, we perform MD simulations for a small (10 chains) system to study the MB dynamics, and a large (270 chains) system is also used to calculate the characteristic time. The implementation has two steps[28,32] with a time step dt = 0.001. The volume of the simulation box is first determined in an isobaric simulation at P = 1. Then, this volume is fixed and the simulation is continued in the canonical ensemble using the Nosé–Hoover thermostat. The simulation is under the temperature T = 0.48, which is slightly above the mode coupling theory critical temperature Tc = 0.45.[28] The monomer density is ρm = 1.03. All results are obtained from simulations in equilibrium.
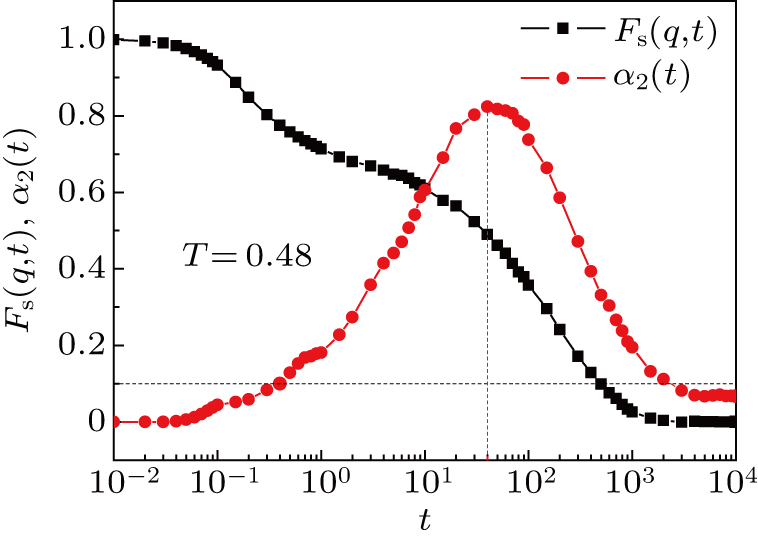
To serve for the study of MB dynamics, a large system (270 chains) is used to calculate the characteristic time at T = 0.48, and twenty independent configurations are simulated for statistical average. An important quantity that is widely used to study the relaxation dynamics is the self-intermediate scatting function
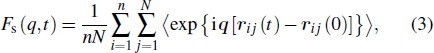 |
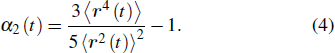 |
The MBs are studied in a single run of the small system (10 chains),[22–24] so that the two types of motion (exploring in an MB and MB–MB transition) are separated in time. In order to identify the MBs, the following distance matrix (DM), which has been described detailedly in Refs. [22] and [23], is calculated:
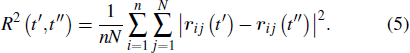 |
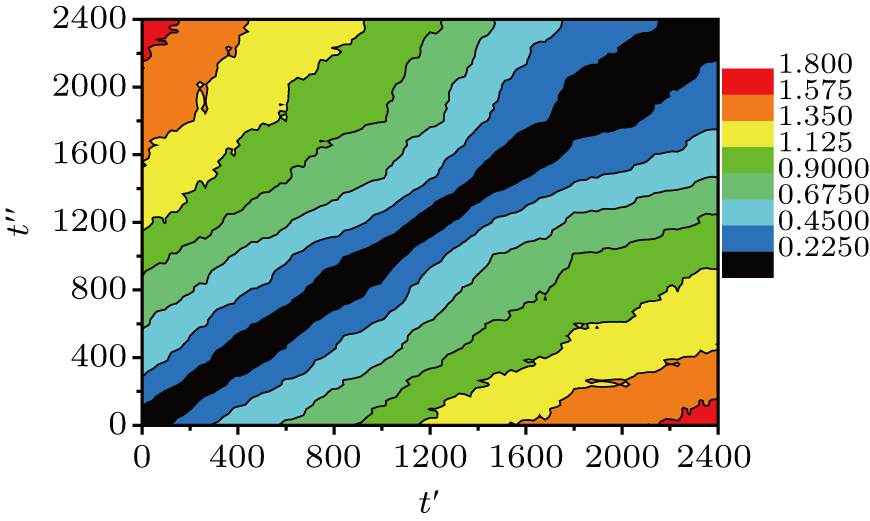
Figure
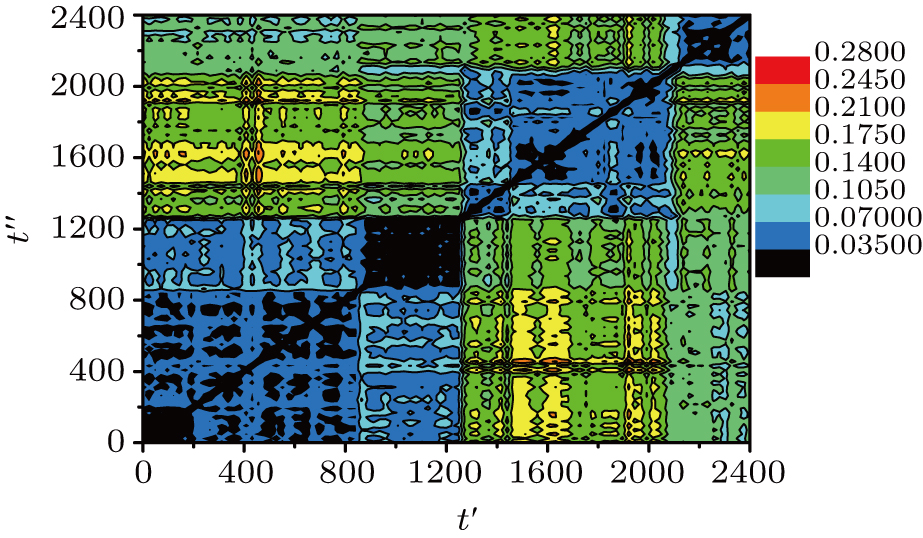 | Fig. 2. Distance matrix R2(t′,t″) of the small system (10 chains) at T = 0.48. The different colors correspond to values of R2(t′,t″) (see the color bar). |
The typical sojourn time within one MB is around 200–400, which is around 50% of τα ≈ 550. So the α-relaxation is realized after several (1–3) MB–MB transitions. We have t* ≈ 40, which is much smaller than the MB sojourn time. Hence, we can conclude that the MB–MB transition is not the main reason of spatially DH, and the same conclusion has been obtained through an experiment of glassy colloidal systems.[25] However, it is different from the BLJM system,[22] in which the time scale of t* corresponds to the sojourn time within one MB, and the MB–MB transitions are relevant for the spatially DH.
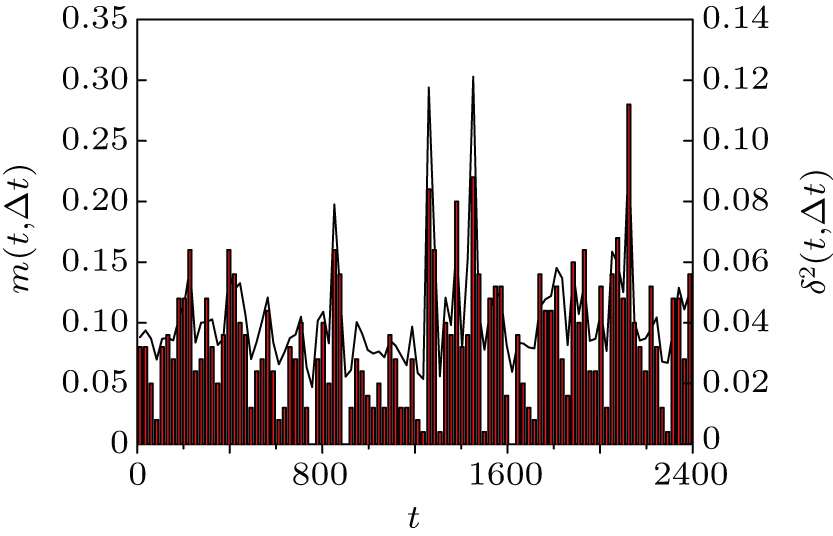
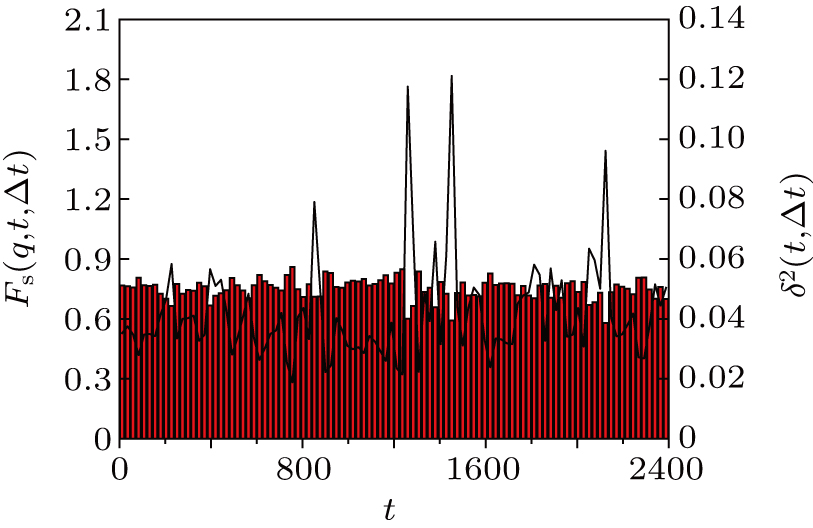
It is also found that the typical sojourn time within one MB is much larger than the MB–MB transitional time. Hence, the dynamics of the system is quite heterogeneous in time, i.e., the system stays for a significant time in an MB before it finds a pathway out. The occurrence of the MB–MB transitions is not regular but random.
To investigate the physical mechanism of MB dynamics, we calculate the averaged squared displacement (ASD) of the monomers within a time interval Δt. It is defined as
 |
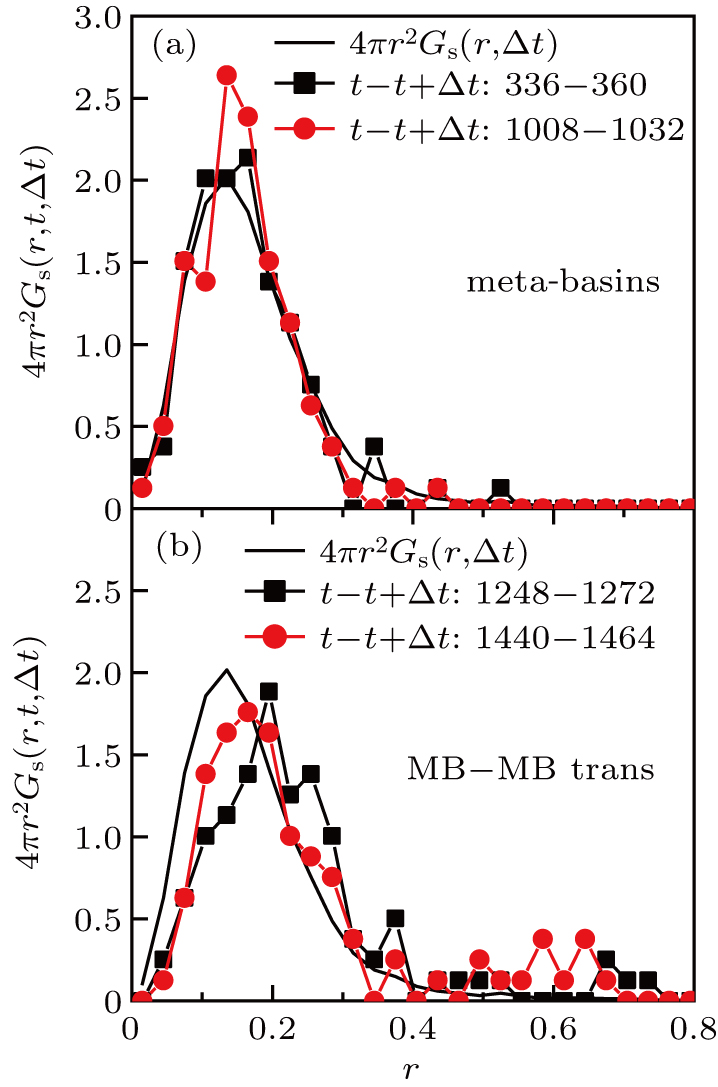
In order to further understand the nature of the motion of monomers when the system leaves an MB, the distribution of the displacement r of the monomers is calculated, which is defined as
 |
To further clarify that the number of monomers that participate in the democratic motion is indeed substantial, the number fraction of mobile monomers is extracted by integrating the distribution of Gs (r,Δt) from rth = 0.30 to infinity and gets 0.065. From Fig.
In order to study the relation between the structural relaxation and MB dynamics, we define the following function:
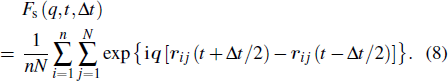 |
To check whether the MB dynamics appears in large systems, the DM of a large system (270 chains) is shown in Fig.
The metabasin dynamics of the supercooled polymer melt is investigated by molecular dynamic simulation. In a small system, the α-relaxation process is composed of a few crossing events that the monomer hops from one metabasin to another. Each crossing event is very rapid and involves a democratic movement of many particles. Evaluation on the contributions of metabasin exploration and democratic movement shows that the structural relaxation is mostly governed by the latter. The dynamics of a small system is heterogeneous in time, i.e. the averaged motion does not evolve gradually with time but exhibits rapid bursts of mobility signaling a democratic movement of many particles. The MB–MB transitions of different small parts of the large system appear randomly. Hence, the relaxation of the large system is gradual on average. At last, we note that the metabasin dynamics are also found for the BLJM model[22] and colloidal suspension experiment.[25] Through comparing the maximum non-Gaussian time with the sojourn time of metabasin, our polymer melt simulation and the colloidal suspension experiment[25] show that the metabasin–metabasin transitions are not the main reason of spatially dynamical heterogeneity. However, the metabasin–metabasin transitions of the BLJM model[22] are relevant for the spatially dynamical heterogeneity.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] |