† Corresponding author. E-mail:
Project supported by the National Key Research and Development Program of China (Grant No. 2017YFA0304203), the National Natural Science Foundation of China (Grant Nos. 61675120, 11434007, and 61875110), Project of the National Natural Science Foundation of China for Excellent Research Team (Grant No. 61121064), the Shanxi “1331 Project” Key Subjects Construction, PCSIRT, China (Grant No. IRT 17R70), and the 111 Project, China (Grant No. D18001).
Optical nanofiber (ONF) is a special tool for effectively controlling coupling of light and atoms. In this paper, we study the ladder-type electromagnetically induced transparent (EIT) under ultralow power level in a warm cesium vapor by observing the transmission of ONF that couples the 6S → 6P Cs atoms in the presence of a 6P → 8S control beam through the same fiber. The linewidth and transmission of the EIT signal are investigated at different intensities of the control laser. In addition, we theoretically study the nonlinear interaction at the ONF interface using the multi-level density matrix equations, and obtain good agreements between theory and experiments. The results may have great significance for further study of optical nonlinear effect at low power level.
Researchers have been working on how to realize the nonlinear photon–atom interaction at low power, a topic of great importance in both nonlinear optics[1] and quantum optics.[2,3] To enhance the nonlinear effects, the nonlinear optical polarization of matter can be enhanced by quantum interference. A famous example is electromagnetically induced transparency (EIT).[4] On the other hand, an efficient way to enhance the nonlinear effect of low light is to reduce the mode volume. Approaches toward this direction including confining light in waveguides and cavities, where photonic band-gap fiber, integrated waveguide or optical nanofiber (ONF) can achieve this characteristic very well.[5–12] There are also researches that combines the two methods, so as to explore quantum interference-enhanced nonlinear effects with confined light field.[13,14] In this work, we use nanofiber to study the EIT effect at ultralow power, which belongs to this category as well. Compared with other structures, the nanofiber can confine the light field more tightly in the surface of fiber, forming the tightly-confined evanescent optical mode interacting with surrounding atoms at long distance.[11,15] This property of ONF provides a new platform for studying nonlinear effects at ultralow power.
The electromagnetically induced transparency is a special nonlinear effect exhibited by the interaction between light and matter. The absorption of the weak probe field at the resonant frequency is reduced when a strong control field is used.[4,16–18] The EIT effect can be widely used in four-wave mixing,[19–21] all-optical switching,[22,23] slow light, and optical storage.[24,25] Recently, researchers have demonstrated EIT phenomenon in cold atoms ONF-based systems at ultralow power, and achieved the optical storage at the single photon level by the Λ-type EIT.[26,27]
In this paper, we use an ONF-based system with hot cesium (Cs) atomic vapor to study the three-level ladder-type EIT phenomenon at ultralow power. This system is simpler than the cold atom system, and we can still observe obvious EIT phenomenon with a few microwatts of the control laser. The probe laser field couples the transition of 6S1/2 → 6P3/2, and the control laser field couples the 6P3/2 → 8S1/2. The EIT spectrum with Doppler-broadened background is obtained by scanning the frequency of the probe laser and fixing the frequency of the control laser when both lasers propagating in opposite directions. The transmission and linewidth of the EIT window as a function of the control laser power are also investigated. To systematically study the EIT effect, we numerically simulate the EIT spectrum by solving the steady-state density-matrix equations and integrating over the atomic velocity distribution. The simulation results show a good agreement with the experimental measurements.
We use the “flame-brush” technique with a hydrogen–oxygen flame to produce ONFs from standard fiber (Fiber Core SM800 5.6/125).[28,29] The nanofiber for the experiment is composed of three parts: the input and output sections composed of a standard fiber, the 5-mm nanofiber regime with 500-nm diamter, and two tapered fiber regimes that smoothly connect the two parts. The simple structure of ONF is shown in Fig.
In our system, ONF is mounted on a U-shaped bracket and placed in a vacuum system filled with Cs vapor, and release the atomic vapor by applying a current to the Cs dispenser. In order to reduce transmission losses due to the accumulation of atoms on the nanofiber surface, we maintain the fiber temperature with special heater element and keep the temperature of the fiber slightly higher than the vacuum chamber.[30] Figure
The schematic diagram of our experimental scheme is shown in Fig.
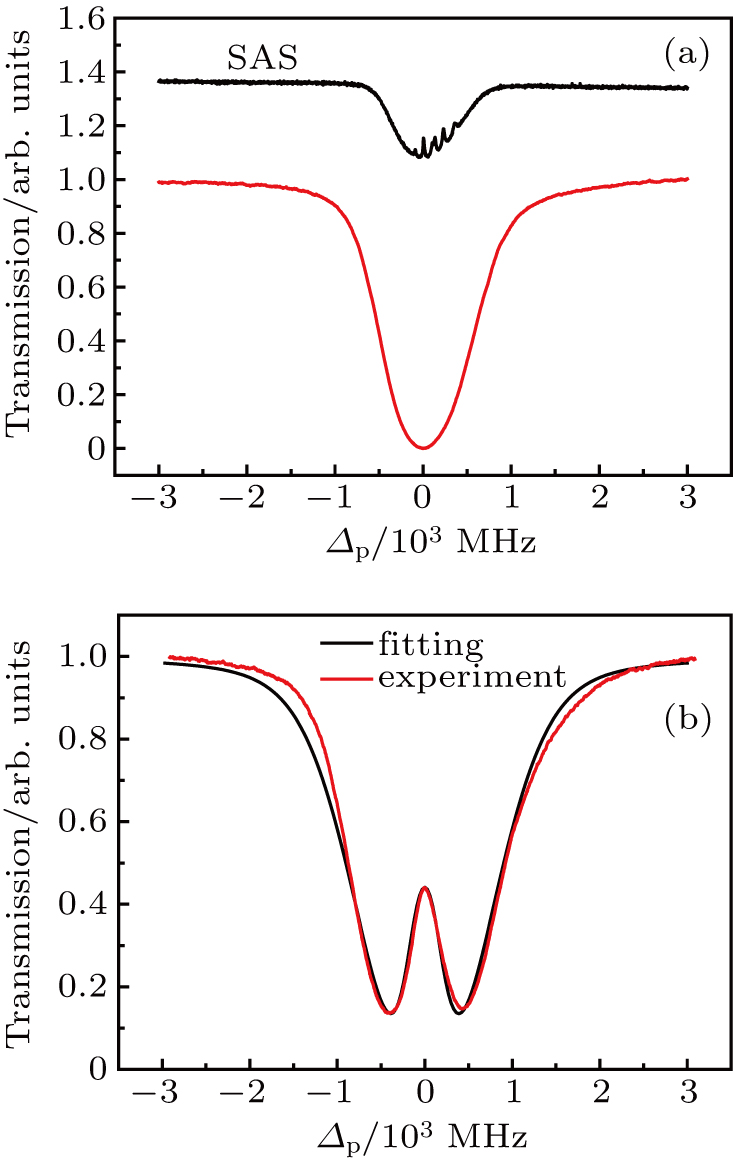
The red line in Fig.
To get a better understanding of physics behind this observation, we numerically solve the density matrix equation, taking into account the velocity distribution of atoms, and compare the numerically evaluated results with the experimental observations. Start from a three-level model as shown in Fig.
In the weak probe limit, the matrix element ρ21 is obtained by solving the above equation with first-order perturbation approximation[31,32]
 |
In our experiment, the probe laser and control laser are counter-propagating and the Doppler shift needs to be considered due to their large frequency difference. In the Doppler-broadened system, when the atom with velocity ν moves toward the probe laser, the detuning Δp of the probe laser should be substituted by Δp + ωpν/c and the detuning Δc of the control laser should be substituted by Δc − ωcν/c.[32] The absorption characteristic of the atomic medium is determined by the imaginary part of total susceptibility[31,32]
 |
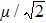
To investigate the effect of control power on the full width at half maximum (FWHM) and transmission intensity of EIT window, the different control powers are used and the probe power is fixed at 1.5 nW. The black dots with error bars in Fig.
 |
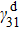
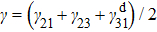
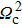
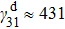
Figure
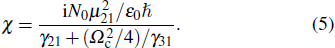 |
In conclusion, we study the three-level ladder-type EIT effect using a nanofiber–Cs vapor interface in the presence of Doppler-broadened and using very low-power probe and control laser beams. We use density matrix equations to numerically reproduce the experimental observations, showing fairly good agreements between the simple theory and experimental observations. The benefit of light confinement in ONF should allow other type of nonlinaer optical experiments, in addition to the ladder-type EIT as in this work. This study may also contribute to realization of EIT-based low-light level optical switch and optical memory.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] |