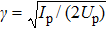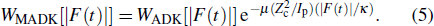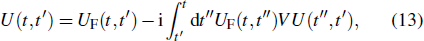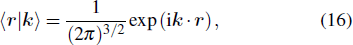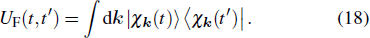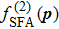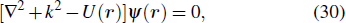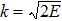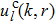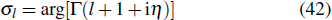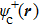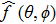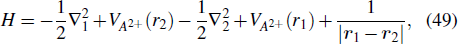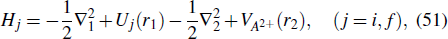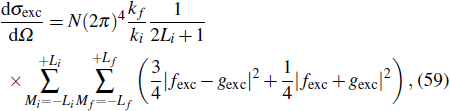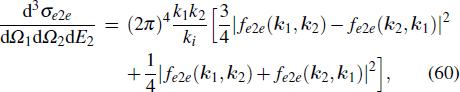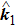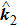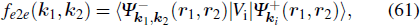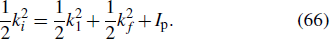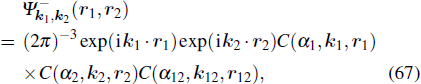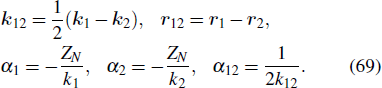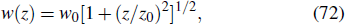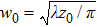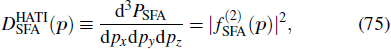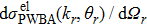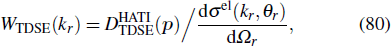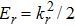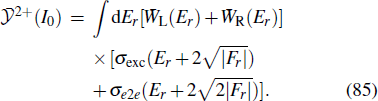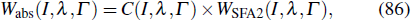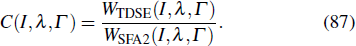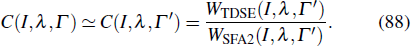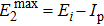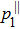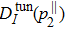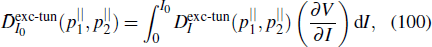1. IntroductionNonsequential double ionization (NSDI) of atoms in strong laser fields has attracted considerable interest both experimentally and theoretically for more than three decades, and still remains one of the most interesting and challenging topics in strong-field physics. The interest on NSDI was first stimulated by the early measurements of the number of doubly charged ions of rare gas atoms exposed to intense laser pulses versus the peak laser intensity.[1–5] The characteristic “knee” structure observed in experiment provides the distinct evidence for NSDI since double-ionization yields could be several orders of magnitude greater than the prediction by the standard theory based on the assumption that electrons are emitted one by one, with the second ionization independent of the previous one. However, with the only available experimental data for the total yield of doubly charged ion, the mechanisms responsible for the two-electron transition were still a matter of controversy. For example, it was suggested that the second electron could be shaken-off by a nonadiabatic change of the potential caused by the emission of the first electron.[3] Alternatively, it was argued[6] that the first electron, released by tunneling through the potential barrier of the combined atomic and field potential, is driven back to its parent ion by the laser field and ionizes the second electron, in a process analogous to an (e,2e) collision. The debate on the mechanisms responsible for NSDI was further settled by the differential ionization measurements, which were first carried out at the turn of this century, for momentum distributions of the doubly charged ion along the laser polarization direction[7] and the momentum correlations between the two outgoing electrons.[8] Those differential ionization measurements provide more detailed insight into the dynamics of the NSDI process and provide a much improved testing ground for the different theoretical models in the dispute. Nowadays, it has already been widely accepted that the main mechanisms leading to NSDI are the laser-induced recollisional (e,2e) and the recollisional excitation with subsequent ionization of the second electron from the excited state of the parent ion.[9]
Over the past three decades, there have been no shortage of theoretical efforts devoted to NSDI (for a review, see Refs. [10] and [11]). It has been well recognized that five interactions are involved in NSDI: the interactions of the laser field with the two electrons, the Coulomb interactions between the doubly charged ion and the two outgoing electrons, and the electron–electron interaction. All the five interactions are strong and roughly equal in importance, so ideally they must be treated on an equal basis. However, in actual numerical calculations, one has to resort to simplifying approximations to make the calculations tractable. In general, the numerical methods developed for NSDI fall into two categories. The first approach takes the set of fundamental interactions of the electrons and solves the time dependent Schrödinger equation (TDSE) or the time dependent Newton equations (TDNE) for the motion of the two electrons. Indeed, a complete description of NSDI could be obtained by an exact solution of the TDSE. However, it is still a formidable computational challenge because of computer speed and memory requirements, and the results alone would not offer much insight into the basic mechanisms for the double ionization processes. So far, only a very few TDSE calculations, with more or less approximations, have been carried out for NSDI.[12–15] On the contrary, it is easier to solve the TDNE for NSDI,[16] and a number of predictions with at least semiquantitative agreement with a relatively wide variety of experimental data have been achieved.[17,18] The second approach is based on the rescattering model from which conceptual clarity derives more easily, even though this might come at the expense of possible loss of physical reality. Within this framework, the S-matrix theory was first developed by extending the strong field approximation (SFA) for high order above threshold ionization (HATI)[19,20] to double ionization.[21] While the TDSE results contain all possible outcomes, which are mixed together, from a given initial state, the S-matrix theory allows one to select any particular item, and hence is more powerful in identifying the specific mechanisms of the NSDI process. Similarly, a recently developed full quantum theory for NSDI, called quantitative rescattering (QRS) model, is also based on the rescattering model. While laser-induced rescattering processes can be qualitatively interpreted by the classical rescattering model,[6,22] the QRS model provides the quantitative description. In addition, the semiclassical theory including the tunneling effect, indeed, has also been widely recognized as a useful approach to simulate the NSDI.[23–27]
The QRS model was first proposed for HATI,[28,29] in which the momentum distribution of the HATI photoelectron is factorized as a product of the returning electron wave packet (RWP) and the differential cross sections (DCS) for elastic scattering of the returning electron with the parent ion. The only difference between HATI and NSDI is that the returning electron experiences different types of collisions, one is elastic scattering and the other is inelastic scattering including electron impact ionization and electron impact excitation. Based on this philosophy, the QRS model was extended to NSDI.[30–32] The past decade has witnessed great success of the QRS model in dealing with various laser-induced rescattering processes.[33,34] Recently, the QRS model for NSDI has been further improved[35–39] by taking into account the lowering of threshold due to the presence of electric field at the instant of recollision.[40]
In this review, we will limit ourselves to the presentation of the improved QRS model for NSDI and its applications to some of the major experimental observations. This article is organized as follows. In Section 2, we will review the basic theoretical tools used in the numerical simulations. In Section 3, we will present the numerical procedures for the simulations of the total yield of doubly charged ion, the double-to-single ionization ratio, and the correlated two-electron momentum distribution. Finally, a summary and outlook will be given in Section 4.
Unless indicated otherwise, atomic units (a.u.) are used throughout this paper.
2. Basic theoretical tools2.1. Theoretical model for single ionization rateIonization of atoms is the first step of the laser-induced rescattering processes such as HATI,[41] high-order harmonic generation (HHG),[42] and NSDI.[5,8]
In general, two mechanisms have been classified for ionization of atoms exposed to an intense laser field by using the Keldysh parameter[43]
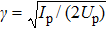, where Ip is the ionization potential and Up is the ponderomotive energy. In the multiphoton ionization regime when γ > 1, an atom absorbs more photons than the minimum number required for the ejection of an electron, leading to the the characteristic above-threshold ionization (ATI) peaks in the photoelectron energy spectra which are separated by the photon energy, while their positions are shifted by the ponderomotive potential. On the other hand, at higher laser intensities, when γ < 1, the liberation of an electron is understood to proceed through tunneling ionization.
The most commonly used theory for ionization of atoms by a linearly polarized laser field is the Ammosov–Delone–Kainov (ADK) approach,[44] which is generally valid for tunneling ionization when the adiabaticity parameter γ is lower than 1.
Suppose an atom is exposed to a linearly polarized laser pulse (along the z axis) with carrier frequency ω and the carrier envelope phase (CEP) φ, the field can be expressed as
for the time interval (−
τ/2,
τ/2) and zero elsewhere. According the ADK model, the ionization rate of the atom at time
t is given by
where
In the above equations,
κ = (2
Ip)
3/2,
n* =
Zc(2
Ip)
−1/2 is the effective quantum number with
Zc being the charge of the residual ion,
l* =
n* −1 is the effective orbital quantum number, and
l and
m are the orbital and magnetic quantum numbers of the valence electron of the atom, respectively.
The ADK model has also been generalized to molecular systems.[45] However, Tong and Lin[46] found that the ADK rates significantly overestimate the numerically calculated static ionization rates for atoms in the barrier-suppression regime, hence they modified the original ADK model to extend the ADK rates from the tunneling ionization region to the near- and over-the-barrier regimes by introducing an empirical correction factor. The modified ADK rate w[|F(t)|] is given by[46]
The fitted parameter
μ in Eq. (
5) for a few atoms and ions has been given in Ref. [
46], which is in the range of 6 <
μ < 10.
The ADK model represents the limit when γ → 0 of the theory proposed by Perelomov, Popov, and Terent’ev (PPT),[47] which is valid for arbitrary γ values. In the PPT model, the ionization rate reads
where
The details about the coefficients
Am(
ω,
γ) in Eq. (
6) can be found in Refs. [
48] and [
49].
With the calculated ionization rate, one can obtain the total ionization probability by a laser pulse as
where
m stands for ADK, MADK, or PPT.
2.2. The strong field approximationThe strong field approximation is a very effective tool to deal with the interaction of atoms with strong laser field. While the SFA can also be used to obtained the total ionization probability of an atom by a laser pulse, it further provides a fairly good quantitative description of the photoenergy spectra as well as the momentum distributions. In general, the SFA model is valid when Ip ≤ 2Up. This condition implies that when the electron appears in the continuum it is only under the influence of a very strong laser field. In addition, when the electron comes back to the parent ion it has a large kinetic energy, so that the Coulomb force of the atomic potential can be neglected.
In the length gauge and the dipole approximation, the laser–electron interaction can be expressed by
Within this approximation, the exact expression for the probability amplitude of detecting an ATI electron with momentum
p and kinetic energy
E =
p2/2 can be written formally as
[50]
where
Ψ0(
t) and
Ψp(
t) are the ground state and a scattering state with asymptotic
p, respectively, of the atomic Hamiltonian
and
U(
t,
t′) is the time-evolution operator of the complete Hamiltonian
The time-evolution operator satisfies the Dyson equation
where
UF(
t,
t′) is the time-evolution operator corresponding to the Hamiltonian of a free electron in the laser field, which is
The eigenstates of the time-dependent Schrödinger equation with the Hamiltonian
HF(
t) are the Volkov states
where
A(
t) is the vector potential of the laser field
F(
t), |
k〉 denotes a plane wave state
and the action
Sp(
t) reads
The Volkov time-evolution operator is then given by
Introducing the strong field approximation, i.e., replacing 〈Ψp(t)|U(t,t′) with 〈χk(t)|U(t,t′) in Eq. (10), and truncating the full time-evolution operator U(t,t′) after the second term, one obtains the SFA ionization amplitude as
where the first term
corresponds to the standard SFA, and the second term
is the first order correction to the standard SFA which consists of ionization, propagation in the continuum, and the interaction of the returning electron with the parent ion.
The form of fSFA(p) in Eq. (19) allows one to identify the contribution from each individual term. If
is dropped in Eq. (19), the standard SFA result can be obtained. For convenience, the standard SFA is referred to as SFA1, while the result from keeping
only in Eq. (19) is referred to as SFA2.[20] The details of numerical procedures for evaluation of the probability amplitude have been presented in Refs. [19], [20], and [51].
It should be noted that, in the numerical calculations, one needs to use a short-range potential
where
α is a parameter introduced to avoid the singularity in
.
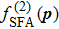
The angular and momentum distribution of an electron emitted in the direction of
is given by
For a linearly polarized laser field, the system has cylindrical symmetry. As a result, the two-dimensional momentum distribution is defined as
where
and
θ is the angle between the polarization axis of the laser field and the direction of the ejected photoelectron. Obviously, the integration over the azimuthal angle
φ has been carried out in Eq. (
24). Furthermore, by integrating over
θ, we obtain the energy spectra
It should be noted that the numerical results depend on the screening factor α. It has been found that the photoelectron energy spectra of SFA2 at low energies increase very rapidly as α decreases. Nevertheless, in the high energy regime, when E > 4Up, the dependence becomes relatively weak, and the shape of the energy spectra almost remains the same. Usually, in the numerical calculations, the value of α is chosen in such a way that direct ionization (SFA1) dominates the photoelectron spectra for the energies bellow 2Up.[52,53]
2.3. The time-dependent Schrödinger equationWhile the SFA allows for intuitive physical interpretation of the intense laser–atom interaction, the numerical solutions of the time-dependent Schrödinger equation, in principle, provide a full quantum description of various phenomena, including the ATI spectra, for an atom in a strong laser field. Within the single-active-electron approximation, the TDSE for single ionization of an atom in the presence of a linearly polarized laser field can be written, in the length gauge, as
where
Hi and
Ha are the laser–electron interaction and the atomic Hamiltonian given by Eqs. (
9) and (
11), respectively. The above time-dependent equation is solved by using a second-order split operator method
[54,55]
and the wave function is expanded by the direct products of discrete variable representation basis sets
[56–58] associated with the Legendre polynomials.
The probability amplitude is obtained by projecting the total final wave function at the end of the laser pulse onto eigenstates of a continuum electron with momentum p
where the continuum state
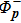
is the outgoing asymptotic Coulomb wave function satisfying the following equation:
Indeed, by solving the TDSE one can obtain the most accurate numerical results provided that the calculations are practical. Unfortunately, the TDSE calculations require a large amount of computing time and are impractical for long pulses at high intensities, so that results can only be obtained for a restricted regime of laser parameters. In addition, the insight into physics is hidden even though the numerical solutions of TDSE can be obtained.
2.4. Standard potential scattering theoryThe QRS model was first proposed for HATI[28] in which laser-induced elastic scattering of electron with the parent ion plays a decisive role.[29,59,60] In this section, we briefly summarize the standard potential scattering theory which has been well documented in the text books; see Refs. [61] and [62], for example.
The scattered wavefunction of an electron by a potential V(r) satisfies the time-independent Schrödinger equation
where
U(
r) = 2
V(
r) is the reduced potential and
k is the momentum, related to the electron energy by
.
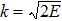
For a short-range potential which falls faster than r−2 as r → ∞, the wavefunction of the scattered electron in the asymptotic region is given by
where
f(
θ,
ϕ) is the scattering amplitude.
To get the scattering amplitude, we solve Eq. (30) by expanding the scattered wavefunction in partial waves
where
Ylm is a spherical harmonic. We take the convention that all continuum waves are normalized to
δ(
k −
k′). The radial equation that
ul(
k,
r) satisfies can be obtained from Eq. (
30) as
Here, we assume that the potential is radially symmetric, i.e.,
V(
r) =
V(
r).
For a plane wave when V(r) = 0, the radial component ul(k,r)/kr in Eq. (32) is a standard spherical Bessel function jl(kr).
When r → ∞, the boundary condition satisfied by ul(k,r) for V(r) = 0 is
while for a short-range potential
V(
r),
From Eqs. (
34) and (
35) we see that it is the quantity
δl, called the phase shift, that displays the influence of the interaction.
By matching the coefficients of the outgoing spherical waves in Eqs. (32) and (31), and using Eqs. (34) and (35), one finds that the scattering amplitude is independent of ϕ and given by
where
Pl(cos
θ) are the Legendre polynomials.
For the scattering by a pure Coulomb potential
where
Z1 and
Z2 are the charges of the projectile and the target, respectively, the method of partial waves is of little interest, since the Coulomb interaction drops off so slowly for large
r. Fortunately, it can be treated in parabolic coordinates and the scattering amplitude can be obtained analytically
where
However, for a real situation frequently encountered in electron scattering in which a short-range potential V(r) is added to a pure Coulomb potential Vc(r) due to decreasing screening of the nucleus of the target ion by its electrons, one still needs to resort to the partial wave decomposition. Similarly, we expand the wavefunction as
and find that the radial wave equation for
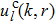
reads
where the quantity
is called the Coulomb phase shift. The asymptotic boundary condition satisfied by the scattered wavefunction
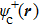
is
Here,
ϕc(
r) is the Coulomb wavefunction given by
The boundary condition satisfied by
when r → ∞ is
Again, the phase shift
δl is due to the short-range interaction
V(
r). Similarly, the scattering amplitude
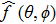
in Eq. (
43) can be obtained by matching the coefficients of the outgoing spherical waves in Eqs. (
40) and (
43) with the help of Eq. (
45)
Therefor, the scattering amplitude for the general case is given by
and the elastic scattering DCS for a given incident energy reads
2.5. Theoretical model for electron impact excitationLaser-induced electron impact excitation is one of the main mechanisms in NSDI. To simulate the correlated two-electron momentum distributions based on the QRS model, one needs to calculate the DCSs for electron impact excitation of parent ions.
The distorted-wave Born approximation (DWBA) is one of most efficient methods dealing with inelastic collision processes. In this section, we briefly review the DWBA method for electron impact excitation of singly charged ion.
Suppose we have an electron with momentum ki which collides with an atomic ion A+, after the collision, the scattered electron has momentum kf, and one bound electron in the ground state is promoted to an excited state (nl). In the frozen core approximation, the exact Hamiltonian for the whole system is given by
where
r1 and
r2 are the position vectors for the projectile and the bound state electron with respect to the nucleus, respectively, and
VA2+ is the effective potential based on the single active electron approximation.
Both the exact initial state wavefunction Ψi(r1,r2) and the final state wavefunction Ψf(r1,r2) of the system satisfy the Schrödinger equation
where
E is the total energy of the system. Since equation (
50) cannot be solved analytically, we form approximate Hamiltonians, which can be expressed as
where
Ui (
Uf) is the distorting potential used to calculate the wavefunction
χki (
χkf) for the projectile in the incident (exit) channel with momentum
ki (
kf). With this approximation, the initial (final) state wavefunction can be expressed as a product of the initial (final) state wavefunction for the projectile and the wavefunction for the bound electron in the ground (excited) state.
The wavefunctions for the electron in both initial ground state Φi(r2) and final excited state Φf(r2) satisfy the differential equation
where
εj (
j =
i,
f) are the corresponding eigenenergies of the initial and final states. The wavefunctions for the projectile in the initial and final states can be obtained by solving the following equation:
Due to the energy conservation, we have
The distorting potentials Ui and Uf used in Eq. (53) play an important role in the numerical calculations, since the calculated DCSs are sensitive to the distorted wavefunctions describing the projectile. Unfortunately, neither Ui nor Uf is determined directly by the formalism. Here, we use the static potentials which are obtained by averaging over the motion of the active electron
Obviously, the distorting potentials given by Eq. (
55) for electron impact excitation of singly charged ion are Coulomb potential asymptotically.
In DWBA, the direct transition amplitude for excitation from an initial state Φi to a final state Φf is given by
where
Vi is the perturbation interaction
And the exchange scattering amplitude is given by
To evaluate the scattering amplitude, we perform the standard partial wave expansions. The details of numerical calculations for the scattering amplitude have been presented in Ref. [63]. Finally, the spin-averaged differential cross section for electron impact excitation from (Ni,Li) to (Nf,Lf) is given by
where the prefactor
N denotes the number of electrons in the subshell from which one electron is excited.
The DWBA is a relatively simple model with respect to other sophisticated theoretical models, such as R-matrix method[64] and convergent close-coupling (CCC) approach.[65] For the calculations of correlated two-electron momentum distributions of NSDI at high laser intensities, the DWBA model is a good candidate since it can be calculated very quickly. Furthermore, the main important physics has been considered in DWBA such that the shape of the DCS is typically in fairly good agreement with the experimental measurements. However, it is well known that, at low energies, the total cross sections (TCS) predicted by the DWBA significantly exceed the experimental values, especially at energies near the threshold, which implies that the DCSs of DWBA are also larger than the absolute experimental data. This suggests that the DCSs of DWBA at low energies require a special treatment before they are used to simulate the parallel momentum distributions for the returning electron after recollisional excitation of the parent ion. This special treatment has been accomplished by introducing a calibration procedure for DWBA.[66]
2.6. Theoretical model for electron impact ionizationNow we consider electron impact ionization which is another dominant mechanism in NSDI. Different from the process of electron impact excitation, in (e, 2e) process, there are two outgoing electrons. Suppose we have an electron with momentum ki which collides with a singly charged ion in its ground state; after the collision two outgoing electrons with momentum k1 and k2 are detected in coincidence. For this process, the triple differential cross section (TDCS) is given by
where
Ω1(
θ1,
ϕ1) and
Ω2(
θ2,
ϕ2) are the solid angles of detectors for the two electrons leaving the collision along
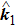
and
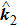
, and
fe2e(
k1,
k2) and
fe2e(
k2,
k1) are the transition amplitudes for the direct and exchange processes, respectively. In the prior form, the direct transition amplitude of the (
e, 2
e) process is expressed by
where
Vi is the perturbation interaction given in Eq. (
57), and
r1 and
r2 are the position vectors of the projectile and the bound state electron, respectively, with respect to the target nucleus.
2.6.1. The DWBA modelSimilar to electron impact excitation, the transition amplitude for the (e, 2e) process can also be evaluated by using the DWBA model. The initial state wavefunction is exactly the same as that for electron impact excitation, i.e.,
In DWBA, the asymptotic final state wavefunction for the two outgoing electrons is expressed as
The wavefunctions for the two outgoing electrons satisfy the following equations:
Due to the energy conservation, we have
The standard partial wave expansions are also made to evaluate the scattering amplitude for (e, 2e). For details, see Ref. [67].
Again, the DWBA model for (e, 2e) is also only valid at high impact energies since the final-state electron–electron interaction, which is important in the collision process at intermediate and low energies, has not been taken into account. The group of Madison has improved the DWBA model by including the final-state Coulomb interaction directly in the final-state wavefunction.[68,69] It has been found that, for intermediate energies, the post-collision interaction between the two outgoing electrons has an important effect and leads to an overall improvement in the agreement between experiment and theory.
2.6.2. The BBK modelFor electron impact ionization of He+ ion, the final-state electron–electron interaction has been taken into account in the Brauner, Briggs, and Klar (BBK) model[70] in which an approximate three-body scattering wavefunction for the final state that satisfies the asymptotic three-body Schrödinger equation (50) exactly was derived analytically. The BBK wavefunction consists of a product of three Coulomb (3C) wavefunctions which is expressed as
where the Coulomb part of the wavefunction is defined as
with
In Eq. (
68),
Γ is the gamma function and
1F1 is the confluent hypergeometric function. If 1/|
r1 −
r2| is dropped in Eq. (
49), the interaction between the two outgoing electrons is turned off. Consequently, the final-state wavefunction becomes a product of two Coulomb (2C) wavefunctions by setting
α12 = 0 in Eq. (
67). It should be noted that the 2C wavefunction, which is equivalent to the asymptotic final state wavefunction in DWBA if the distortion of the short range potential is neglected, does not satisfy the proper asymptotic three-body boundary condition.
In the BBK model which was originally proposed for the process of electron impact ionization of hydrogen, a plane wave is used to describe the incoming electron since the target is neutral. However, for electron impact ionization of He+ ion, a Coulomb wave should be employed to account for the Coulomb attraction between the incident electron and the target ion. The Coulomb wavefunction for the incident electron takes the form
where
αi = −1/
ki. In this case, the transition amplitude involves four Coulomb (4C) wavefunctions. With the precollision interaction between the incident electron and the target ion taken into account, Jia
et al.[71] first carried out the numerical calculations of TDCS for electron impact ionization of He
+ ion at intermediate impact energies.
It should be mentioned that some deficiencies still exist in the BBK wavefunction although it satisfies the asymptotic three-body Schrödinger equation exactly. The major limitation of the 3C wave function lies in the fact that the influence on the strength of the interaction of any two particles by the presence of a third one has not been taken into account. This deficiency was first corrected for the case in which the two outgoing electrons have equal energies by introducing effective Sommerfeld parameters,[72] and was later generalized for any energy sharing in all geometries.[73] Such a modification reflects the dynamic screening of the three-body Coulomb interactions.
2.7. Focal volume averagingNumerical simulations for spectra are usually performed for a single laser intensity. However, when atoms are exposed to a laser field, they experience different intensities across the beam profile. For a Gaussian beam, the intensity distribution is given by
where
and
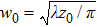
denotes the Rayleigh range of the focus.
Since experiment collects electrons originating from atoms located anywhere in the interaction volume, direct comparison of the experimental data with the theoretical spectra is acceptable only when the focal volume effect has been taken into account. Therefore, integration over the focus volume should be performed by finding the volume of each isointensity shell. For example, the focal volume averaged total yield of single ionization at a peak intensity I0 can be obtained by
where the volume of an isointensity shell between
I and
I + d
I is given by
[74]
with
c1 = [(
I0 −
I)/
I]
1/2 and
c2 = {[
I0 − (
I + d
I)]/(
I + d
I)}
1/2.
3. The quantitative rescattering modelLaser-induced rescattering processes have been well understood based on the three-step classical rescattering model.[6,22] In the first step, the electron tunnels out from an atom. In the second step, the electron moves in the laser field and returns to the parent core. Finally, in the third step, the electron collides with the parent ion. During the collision, both elastic and inelastic scatterings could take place. The elastic scattering of the returning electron with the parent ion leads to HTAI,[75] and the recombination of the returning electron with the parent ion produces HHG.[76] On the other hand, NSDI[77] is due to inelastic scattering of the returning electron by the parent ion, in which two mechanisms could be involved, one is the direct ionization of the parent and the other one is recollision excitation with subsequent ionization. In the simulation of all the laser-induced rescattering processes, the RWP which describes the momentum distribution of the returning electron plays a significantly important role.
3.1. Returning electron wave packetAccording to the QRS model, the momentum distribution of the HATI photoelectron with momentum p is expressed as a product of the RWP and the DCS for elastic scattering of the returning electron with the parent ion.[28,29] By defining
the QRS model for HATI reads
where
W(
kr) is the RWP describing the momentum distribution of the returning electrons, and
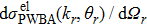
is the DCS, calculated within the plane wave first-order Born approximation (PWBA), for an electron with a momentum of magnitude
kr to be scattered at an angle
θr with respect to the direction of the returning electron.
The detected photoelectron momentum p and the momentum kr of the scattered electron are related by[28]
with
where
Ar ≡
A(
tr) is the instantaneous vector potential at the returning time
tr when the recollision takes place. It should be noted that the relation between
kr and |
Ar| is determined approximately by solving the Newton’s equation of motion for an electron in a monochromatic laser field.
[28] Equation (
28) is an inherent approximation used in the QRS theory but the error is insignificant. This issue has been discussed in detail in Ref. [
28] in which the validity of the QRS model for HATI has also been extensively verified.
The RWP is then obtained by
It has been established[28] that, equation (76) also holds for the HATI photoelectron spectra from the TDSE if the DCS for elastic scattering of electron with the parent ion is calculated based on the standard potential scattering theory. This indicates that the RWP can also be obtained from solving the TDSE, i.e.,
where
Figure 1 shows the RWPs extracted from the HATI photoelectron momentum distributions, calculated by solving the TDSE and using the SFA2, for Ar in 5 fs laser pulses with the wavelength of 800 nm at the intensities of 1.0 × 1014 W/cm2 and 2.0 × 1014 W/cm2, respectively. One can see that the RWP from SFA2 bears a striking resemblance to that from TDSE. Figure 1 also demonstrates that, the RWPs from both SFA2 and TDSE exhibit no dependence on the rescattering angle θr. This property indicates that one only needs to calculate the RWP at an arbitrary rescattering angle. In the real calculations, usually a large scattering angle, say θr = 170°, is chosen.
Another important property of the RWP is that it is almost independent of the target. Figure 2 displays the RWPs from SFA2 for single ionization of H and Ar in 5-cycle pulses at the intensity of 1.0 × 1014 W/cm2 with the wavelength of 800 nm and the intensity of 0.8 × 1014 W/cm2 with the wavelength of 2000 nm, respectively. Due to the reason stated above, in Fig. 2 the RWPs are extracted from the HATI photoelectron momentum distributions along a fixed outgoing angle θ, which has a one-to-one relation with the rescattering angle θr, and plotted as a function of only the momentum of the returning electron. It can be seen that the RWPs shown in Fig. 2(a) are quite different from those in Fig. 2(b). However, the RWP for H is almost the same as that for Ar for a given laser pulse. This indicates that the RWP depends only on the laser parameters but not on the target. It is well known that the information of both the laser parameters and the atomic structure is imprinted in the HATI photoelectron momentum spectra. Nevertheless, since the RWP only depends on the laser field and the DCS is totally determined by the target, the QRS model, as it is expressed by Eq. (75), can be used to extract the information of the target structure from the HATI photoelectron momentum spectra measured in experiment.[78–80]
3.2. Total yield of doubly charged ionThe QRS model for NSDI was first applied to the calculations of the total yield of doubly charged ion.[30] The total yield of doubly ionization due to NSDI in a linearly polarized laser pulse at a single peak intensity I can be expressed by
where
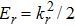
is the energy of the returning electron,
σexc(
Er) and
σe2e(
Er) are the TCSs for electron impact excitation and ionization from the ground state of the target ion, and
WL(
Er) and
WR(
Er) are the returning electron wave packets extracted from the “left” (
pz < 0) and the “right” (
pz > 0) sides of the 2D momentum distributions for the HATI photoelectrons, respectively. For long pulses considered here,
WL(
Er) =
WR(
Er).
As mentioned in Subsection 2.7, to compare with experiment, the focal volume effect has to be taken into account. However, since the total cross sections σexc(Er) and σe2e(Er) in Eq. (82) do not depend on the laser parameters, the focal volume integral has only to be performed for the returning electron wave packets. Therefore, the total yield for the doubly charged ion at the peak intensity I0 can be obtained by
where
are the focal volume averaged wave packets.
In Fig. 3, the simulated results by using Eq. (83) for the yields of doubly charged ions for NSDI of He in a linearly polarized laser pulse at 780 nm with the pulse duration of 120 fs[35] are compared with the experimental measurements of Walker et al.[5] In the numerical calculations, the returning electron wave packets and the total cross sections are evaluated by using the SFA2 and the R-matrix theory,[81] respectively. It can be seen from Fig. 3 that, while the model results are in good agreement with experiment in the regime of intermediate intensities, the QRS model fails to reproduce the total yield of doubly charged ion at both low and high intensities. This clearly indicates that the QRS model should be improved when it is applied to NSDI.
According to the classical rescattering model, the maximum kinetic energy that a returning electron can gain from the field is 3.17Up, which is proportional to the laser intensity. This indicates that a minimum intensity, referred to as the threshold intensity, is required for the returning electron to have enough energy to ionize an electron of the residual ion or to promote this electron to an excited state. Nevertheless, this threshold intensity has never been observed in experiment.[82] van der Hart and Burnett[40] argued that the incorrect threshold intensity appears from the assumption in the recollision model that scattering can be treated as if it takes place in a free atom. As a matter of fact, this assumption is not true. In a free atom or ion, an incoming electron can promote the ground-state electron to an excited state and remain a continuum electron only when its kinetic energy is larger than the energy difference between the ground state and the excited state, since the total energy of a continuum electron must be positive. In contrast, in the case when the collision takes place in an electric field, the combined atomic and electric potentials form a barrier below zero. As a result, the projectile electron can escape from the atom or ion even with negative energy as long as its energy is higher than the potential barrier.[40] Therefore, in the laser-induced recollision process, electron impact excitation of the parent ion can still take place even when the returning electron has an energy less than the energy difference between the ground state and the excited state. This phenomenon is usually referred to as “lowering of threshold”. This does not mean, however, that the energy level of an excited state is lowered.
The maximum barrier height in the combined Coulomb and electric field potentials is given by[40]
where
Zeff is the effective charge of the Coulomb potential seen by the projectile electron asymptotically, and
Fr is the electric field at the instant of collision. For electron impact excitation and ionization of a singly-charged ion,
Zeff = 1 and 2, respectively. Thus, for electron impact excitation and electron impact ionization taking place in an electric field, the threshold is lowered by |
Vb|.
Unfortunately, it is still a formidable task to perform actual numerical calculations with the lowering of threshold included. Alternatively, van der Hart and Burnett[40] suggested that, to account for the lowering of threshold, one should adjust the collision energy so that the returning electron energy Er (=Ei) corresponds to the incoming energy Er + |Vb| for electron impact excitation and ionization in the field-free case. Based on these considerations, the QRS model could be improved, and thus equation (83) should be modified as
Furthermore, since the barrier height of the combined atomic and electric field varies with the time when the laser-induced electron returns to the origin, an “average” returning time is chosen to make the calculations tractable. The method used to determine the average returning time was described in Ref. [
37]. For example, by choosing an average returning time of
ω tr = 290°, one obtains the maximum shifts for the threshold energies of 21 eV and 15 eV, for ionization and excitation, respectively, at a laser peak intensity of 15 × 10
14 W/cm
2.
As demonstrated in Fig. 3, by using Eq. (85) with the lowering of threshold taken into account, the improved QRS model successfully reproduced the the total yield of the doubly charged ion measured in experiment at low intensities. However, as also seen from Fig. 3, the threshold shift does not improve the model results at high intensities. In contrast, the agreement between the simulations and measurements at intensities above 9.0 × 1014 W/cm2 becomes even worse. This deviation has been traced back to the returning electron wave packet in the region of low energy.[35]
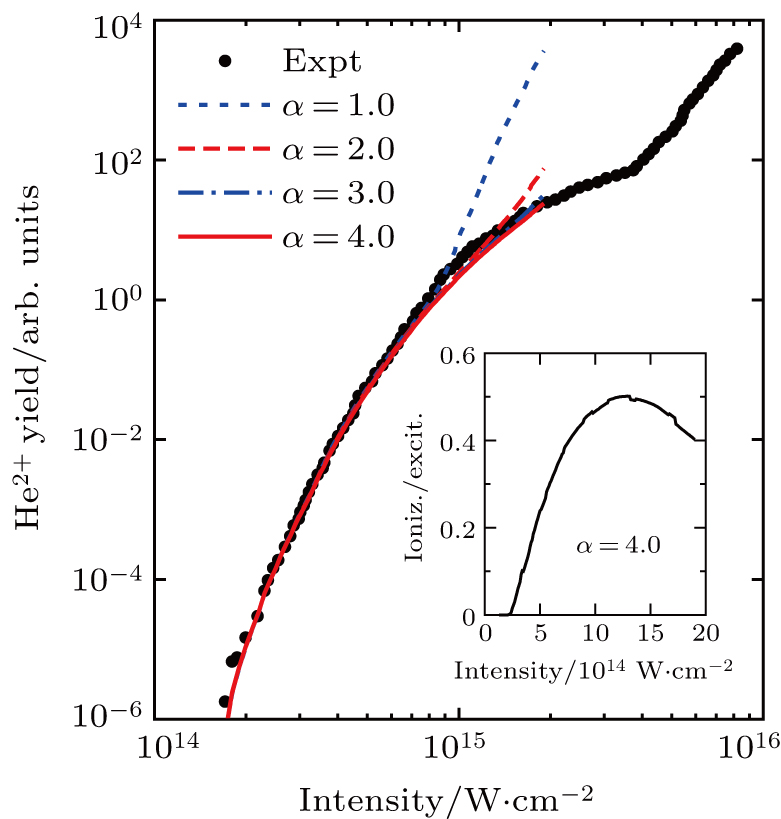
As indicated in Subsection 2.2, a screening parameter α was introduced in Eq. (22) to avoid the singularity in the probability amplitude of SFA2. In Fig. 3, the parameter α = 1.0 was used. It has already been recognized[20] that the HATI photoelectron energy spectra generated by SFA2 are sensitive to the screening factor at low energies (below 2Up), but remain almost the same at high energies (above 4Up). This is also true for the returning electron wave packets obtained from SFA2. Figure 4(a) shows how the RWP changes with the returning energy for α = 1.0 at three peak laser intensities. One can see that each RWP starts with a fast drop at low energies before becoming flat in the plateau region, somewhat mimicking the HATI spectra. The disagreement between theory and experiment in the high-intensity region, shown in Fig. 3, originates from the large magnitude of the low-energy distribution in the RWP. When the excitation threshold is shifted down by the laser field, the low-energy part of the RWP contributes more to double ionization. That is why the simulated results deviate more from experiment when the lowering of threshold energy is included. The dependence of the RWP on the screening parameter is displayed in Fig. 4(b). As it is expected, the screening factor does not affect the RWP in the plateau region. On the contrary, in the low energy region, the RWP decreases substantially with the increase of the screening factor until α = 3 when it is stabilized.
It is found that as α is increased, the model calculations converge to the experimental data, as demonstrated in Fig. 5. The inset of this figure depicts the ratio of ionization with respect to excitation for the production of He2+ ions as a function of the peak laser intensity.
It should be noted that, for He, singlet cross sections for both electron impact excitation and electron impact ionization of the parent ion should be used in the numerical simulations for NSDI, since the two electrons involved in the process start in the singlet ground state, and their singlet coupling is preserved during recollision. This effect is virtually absent in other noble gases with many valence electrons and hence spin-averaged cross sections should be used.
With the improved QRS model, Chen et al.[36] have also simulated the total yields of doubly charged ions for NSDI of He and Ne in intense laser pulses at wavelengths of 390 nm and 400 nm, respectively, and the obtained results are in very good agreement with the experimental data over a broad range of laser intensities.
3.3. Double-to-single ionization ratioWhile double ionization yields versus laser intensity provide the first evidence that strong-field NSDI occurs in favor of the classical recollision model, the measured experimental data are relative. In contrast, the absolute values of the double-to-single ionization ratio can be determined in experiments and hence offer a more stringent test of the theoretical models. Theoretically, to simulate the double-to-single ionization ratio, one needs to obtain the absolute values for both double and single ionization yields.
In the previous section, the RWPs used in the simulations of the double ionization yield are evaluated by using SFA2. Nevertheless, it has been demonstrated[28] that the RWP of SFA2 only has the correct momentum or energy dependence but not the absolute value with respect to the RWP calculated by solving the TDSE. This might indicate that, in order to obtain the absolute total yield of doubly charged ion, one should use the RWP from TDSE. Unfortunately, the TDSE calculations are very time-consuming and very computationally demanding for long pulses at high intensities. Therefore, it is almost impossible to solve the TDSE for the simulations of real experiments, as for the situations considered here. However, since the only difference between the RWPs from SFA2 and TDSE, for a given laser pulse at a peak intensity I with a wavelength λ and a pulse duration Γ, is a normalization factor, it is still possible for one to obtain the correct absolute RWPs by renormalizing the RWP from SFA2 according to[38]
 | |
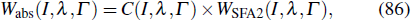where the normalization factor is given by
Nevertheless, the above equations are essentially useless since they only mean that
Wabs(
I,
λ,
Γ) =
WTDSE(
I,
λ,
Γ). However, since the RWPs from SFA2 and TDSE should have the same pulse duration dependence, the normalization factor should not depend on the pulse duration significantly. Consequently, equation (
87) can be approximately rewritten as
The great advantage of the above equation is that it allows one to choose a few-cycle short pulse in the actual calculations for the normalization factor.
To obtain the double-to-single ionization ratio, one also needs to evaluate the total single ionization yield. Several theoretical models, such as ADK, PPT, SFA, and TDSE, can be used to calculate the single ionization yield. All of these theoretical models, except TDSE, are not able to reproduce the correct absolute ionization yields despite that the general trend of the ionization yield as a function of laser intensity can be well predicted by PPT and SFA. Again, this indicates that one also needs to calibrate the PPT or SFA results. For single ionization, a similar procedure could be applied by using the ionization probability from solving the TDSE for a short pulse at low intensity to renormalize the ionization probability from PPT or SFA. Details of the TDSE calculations and the normalization procedure can be found in Refs. [38] and [55], respectively.
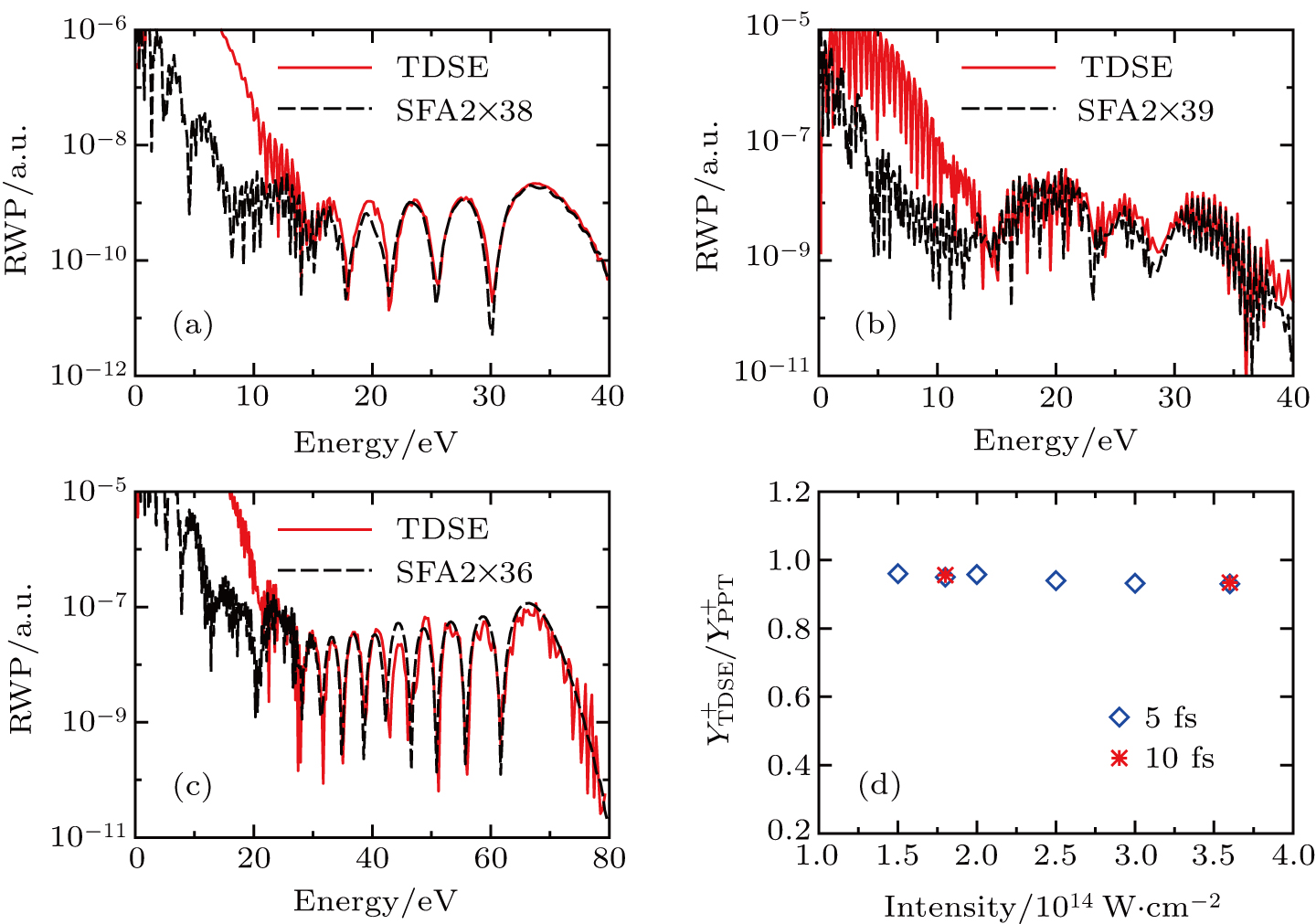
As an example, in Fig. 6 we show the comparison of the returning electron wave packets from TDSE and SFA2 for Ne in a linearly polarized 800 nm laser field as well as the ratio of the single ionization yield from TDSE over that of PPT. From Figs. 6(a)–6(c), one can see that, with appropriate rescaling factors, the RWPs of SFA are in very good agreement with those of TDSE in the plateau region. In addition, it is demonstrated that the normalization factors for different pulse durations and different laser intensities are quite close, which confirms the assumption made in Eq. (88). It should be noted that in the low energy regime, the RWPs of TDSE are much higher than those of SFA2. This is due to the fact that the contributions from direct ionization and laser-induced rescattering cannot be separated in the TDSE photoelectron spectra below 2Up. Similarly, one can see from Fig. 6(d) that, the ratios of
at different intensities are almost constant and very close to 1. This indicates that the PPT theory is a good candidate to evaluate the total single ionization yield, and the ratio of
does not depend on the pulse duration and the laser intensity either.
With the carefully prepared absolute double and single ionization yields, it is straightforward to obtain the double-to-single ionization ratio.
Using the improved QRS model, Chen et al.[35,36,38] have recently calculated the double-to-single ionization ratios for He and Ne in intense fields with various different laser parameters, and the numerical results were found to be in good accordance with the experimentally measured data.[5,82–85] Figure 7 shows the double-to-single ionization ratios simulated by the QRS model for He in a 120 fs pulse with a wavelength of 390 nm and for Ne in a 40 fs pulse with a wavelength of 400 nm, respectively. In both cases, the results of the QRS model are in remarkably good agreement with the experimental measurements[82,83] over the whole range of laser intensity. It should be noted that, in Fig. 7(a) the measured intensities are multiplied by 1.5, as suggested by Parker et al.[12] who performed the corresponding TDSE calculations, and in Fig. 7(b) the experimental data of the double-to-single ionization ratio for Ne were deduced from the total ionization yields of Ne2+ and Ne+ measured by Ekanayake et al.[83] One can see from Fig. 7(a) that the QRS model also reproduces the TDSE results of Parker et al.[12] very well, except for the intensities below 5.0 × 1014 W/cm2. However, the calculations of van der Hart and Burnett,[40] which are also based on the rescattering model, predict a lower intensity dependence especially at low intensities.
Very recently, the QRS model has also been employed to investigate the pulse-duration dependence of the double-to-single ionization ratio of Ne by intense 780-nm and 800-nm laser fields.[38]
3.4. Correlated electron momentum distributionWhile the early measurements of the total ionization yields for doubly charged ions greatly stimulated the investigation of NSDI, the experimental data could only give little insight into the ionization mechanism compared to the correlated two-electron momentum distributions (CMD). Since the first measurement performed by Weber et al.[77] at the turn of this century, the CMD have been shown to provide the most detailed information of NSDI, and hence yield direct and intuitive insight into the dynamics of laser–atom interaction.
In 2010, just two years after it was first development for HATI and HHG,[86] the QRS model was quickly extended to the simulations of CMD for NSDI of He, Ne, and Ar atoms.[31,32,87] Different from the calculations of total ionization yields for doubly charged ions in which only the TCSs for electron impact excitation and electron impact ionization of the parent ion are needed, in the simulations of CMD for NSDI, it is necessary to evaluate the DCSs for the corresponding inelastic collision processes. Consequently, the numerical procedures become much more complicated. Very recently, the QRS model was further improved and the NSDI processes of He were revisited.[37,39]
Within the framework of the present QRS model, the CMD for recollisional (e,2e) process and recollisional excitation with subsequent tunneling of the second electron are simulated separately.
3.4.1 Recollisional (e,2e) processAccording to the QRS model, the CMD for laser-induced (e,2e) collision in NSDI can be factorized as a product of the RWP and the field-free differential cross section for ionization of the parent ion by the impact of the laser-induced returning electron. In experiment, the CMD for NSDI are measured only for the momentum components along the laser polarization axis for the two outgoing electrons. Thus, to compare with experiment, the calculated TDCS for the laser-free (e,2e) process needs to be projected on the polarization axis. For a given incident energy, the two-electron momentum spectra along the incident direction for the laser-free (e,2e) process can be obtained by integrating the TDCS over ϕ2 and E2
where
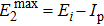
, and
Ip is the ionization potential of the parent ion. In Eq. (
89), we set
ϕ1 = 0 owing to the cylindrical symmetry of the TDCS, and the integration over
ϕ2 is performed only from 0 to
π since the TDCS is symmetric about the plane formed by
k1 and
ki.
For laser-induced recollisional (e,2e) process, the two electrons are still under the influence of the laser field after the collision, and thus at the end of the laser pulse each electron will gain an additional momentum −Ar, where Ar is the vector potential at the time when the recollision takes place. Therefore, by using the relation in Eq. (77) for each of the two outgoing electrons, the CMD for recollisional (e,2e) process in a strong field at an intensity I can be expressed by
where
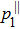
and
are the parallel momenta of the two correlated electrons along the laser polarization, respectively.
Based on the classical simulation[28] for HATI in which laser-induced elastic scattering takes place, the vector potential Ar at the collision time is approximately determined by the relation in Eq. (78). Nevertheless, for laser-induced inelastic collision of the returning electron with the parent ion, as discussed in Subsection 3.2, the threshold energy could be lowered due to the presence of electric field. Since it is extremely formidable to perform the actual numerical calculations including the lowering of the threshold energy, an alternative strategy was suggested by van der Hart and Burnett[40] in which it was assumed that the energy of the incoming electron with respect to the maximum of the barrier in the atomic and electric potential corresponds to the incoming electron energy in the field-free case. Based on this assumption, equation (78) should be modified and rewritten as
where Δ
E = |
Vb| and
Vb is given by Eq. (
92).
To obtain the CMD for a given intensity, one has to consider the contributions from all collisions at different incident energies weighted by the RWP. This gives
where
WI(
Ei − Δ
E) is the RWP in the laser field at a single intensity
I, which can be calculated by using SFA2. We emphasize that the lowering of threshold has been taken into account in Eq. (
92).
Finally, to compare with experimental measurements, the integration over the focus volume should be performed
where
I0 is the peak intensity of the laser field.
We comment that the above numerical procedures for recollisional (e,2e) in NSDI are directly applicable to all rare gas atoms except that for He the spin conservation should be considered such that in Eq. (89) the singlet TDCS should be used. Clearly, the simulated CMD highly depends on the theoretical models employed to calculate the TDCS for laser-free electron impact ionization of the parent ion. For example, very recently, Chen et al.[37] have presented numerical simulations on the CMD for recollisional (e,2e) process in NSDI of helium by a 800 nm laser field at an intensity around 4.5 × 1014 W/cm2 based on the improved QRS model. In the TDCS calculations for (e,2e) on He+, several theoretical models, which are referred to as 2C, 3C, 4C, DS3C, and DS4C, respectively (see Subsection 2.6 and Ref. [37] for details), have been used. The simulated results were compared with experimental measurements of Staudte et al,[14] as shown in Fig. 8. It has been found that while the postcollision Coulomb interaction is responsible for the observed fingerlike structure, the precollision Coulomb interaction changes the orientation of the two fingers from V-type to parallel, and the dynamic screening of the three-body Coulomb interactions in the final state reduces the separation of the two fingers.
3.4.2. Recollisional excitation-tunneling processApart from recollisional (e,2e), another main mechanism in NSDI is recollisional excitation-tunneling. At a single peak intensity, the CMD for recollisional excitation-tunneling of atoms in a linearly polarized laser pulse can be expressed as a product of the parallel momentum distribution for the scattered electron after recollisional excitation and the parallel momentum distribution for tunneling-ionized electron from the excited state.
The parallel momentum distribution for the scattered electron after excitation at a given incident energy Ei can be obtained by projecting the DCS dσexc/dΩ for laser-free electron impact excitation of parent ion onto the polarization direction
where
k1 is the momentum of the scattered electron and
with
θ being the scattering angle. Again, according to the QRS model, the corresponding parallel momentum distribution for the recollisional excitation process taking place in a strong laser field at an intensity
I can be obtained from Eq. (
94) by shifting the momentum of the projectile electron by −
Ar
where
Ar is the vector potential at the instant of recollision, which is related to the returning (incident) electron energy by Eq. (
91).
For tunneling ionization of electron from excited state of the parent ion, several theoretical models, such as ADK, PPT, SFA, and TDSE, can be used to evaluate the parallel momentum distribution. Among all of these theoretical methods, the ADK model is the simplest one. Using the ADK model, the ionization rate, with the depletion effect taken into account, can be expressed as
where
W[|
F(
t)|] is the modified ADK rate given by Eq. (
2) in Ref. [
46]. Assuming that the initial velocity of the tunneling electron is zero, the momentum spectrum for single ionization of the parent ion is given by
With the parallel momentum distributions
for excitation and
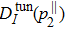for tunneling ionization, the CMD for laser-induced electron impact excitation at incident energy Ei with subsequent tunneling ionization in the laser field at a peak intensity I reads
For a given intensity, in principle, excitation takes place as long as the kinetic energy of the returning electron is larger than the lowered threshold energy. Therefore, similar to recollisional (
e,2
e), an integral over
Ei should be performed to account for the contributions from collisions at all incident energies
where
Iexc is the threshold energy for excitation.
Finally, to compare with experiment, an integration over the focus volume should be performed according to
where
I0 is the peak intensity of the laser field.
As indicated in Eqs. (98) and (99), the CMD for recollisional excitation-tunneling consists of the parallel momentum distribution for the returning electron after collision, the parallel momentum distribution for the electron ionized from the excited state of the parent ion, and the momentum (energy) distribution of the returning electron before collision. Each of the three ingredients plays an important role in the simulations of the CMD.
In a previous work, the CMD for recollisional excitation-tunneling in NSDI of He was simulated by Chen et al.[32] who used the DWBA model to calculate the DCSs for electron impact excitation of He+ while the parallel momentum distribution for tunneling-ionization was evaluated by using the modified ADK model. However, it is well known that, the total cross sections predicted by the DWBA often exceed the experimental values significantly at low energies, even though the angular distribution of the DCS from DWBA calculations is typically in fairly good agreement with experiment. On the other hand, a damping factor was introduced empirically in the modified ADK model. Unfortunately, the damping factor is not available for ionization from the excited states although it has been well estimated for ionization from the ground state of a few atoms and ions.[46]
Very recently, the recollisional excitation-tunneling process in NSDI of helium in 800 nm laser pulse was revisited and the CMD measured by Staudte et al.[14] was re-simulated by Chen et al.[39] using the improved QRS model. In those
CMD simulations, the DCSs for electron impact excitation of He+ were calculated using the state-of-the-art many-electron R-matrix theory, and the tunneling ionization rates for electrons in the excited states were evaluated by solving the TDSE. The calculated CMD is displayed in Fig. 9(a), which demonstrates that the fourfold symmetry with regard to the parallel momentum components is broken. This is in contradiction to the prevalent view that the correlation pattern for excitation-tunneling in NSDI is symmetric with respect to the coordinate axes. Nevertheless, in order to compare with the entire CMD measured in the experiment, the momentum distribution for the recollisional (e,2e) process has to be included. Figure 9(b) shows the CMD for the recollisional (e,2e) process in NSDI of He.[37] By summing the CMD in Figs. 9(a) and 9(b), the predicted CMD for NSDI of He including both recollisional (e,2e) and excitation-tunneling is obtained, as depicted in Fig. 9(c). Figure 9(d) shows the original experimental data of the CMD for NSDI of He.[14] However, by comparing the simulated CMD in Fig. 9(c) with the experimental data shown in Fig. 9(d), one observes that the populations along the axes in the experimental CMD are not reproduced by the QRS model. This is due to the fact that the kinematically allowed regime for the correlated electron momentum components parallel to the laser polarization axis in excitation-tunneling does not reach this region for the case considered here, even with the potential change taken into account. It has been argued[32] that an additional mechanism might be responsible for the distribution along the axes in the CMD which can be separated from the entire CMD measured in the experiment, as displayed in Fig. 9(e). By deducting the CMD in Fig. 9(e) from that in Fig. 9(d), one obtains the “refined” experimental CMD owing to the mechanisms of recollisional ionization and excitation-tunneling only, as shown in Fig. 9(f). Therefore, the simulated CMD in Fig. 9(c) should be compared directly with the corresponding CMD of experiment in Fig. 9(f), and the comparison demonstrates that the theoretical predictions are in fairly good agreement with the experiment.
