Relaxation dynamics of Kuramoto model with heterogeneous coupling
Project supported by the National Natural Science Foundation of China (Grant Nos. 11905068, 11847013, 11175150, and 11605055), Postgraduate Research and Practice Innovation Project for Graduate Students of JiangSu Province, China (Grant No. KYCX18-2100), and the Scientific Research Funds of Huaqiao University, China (Grant No. 605-50Y17064).
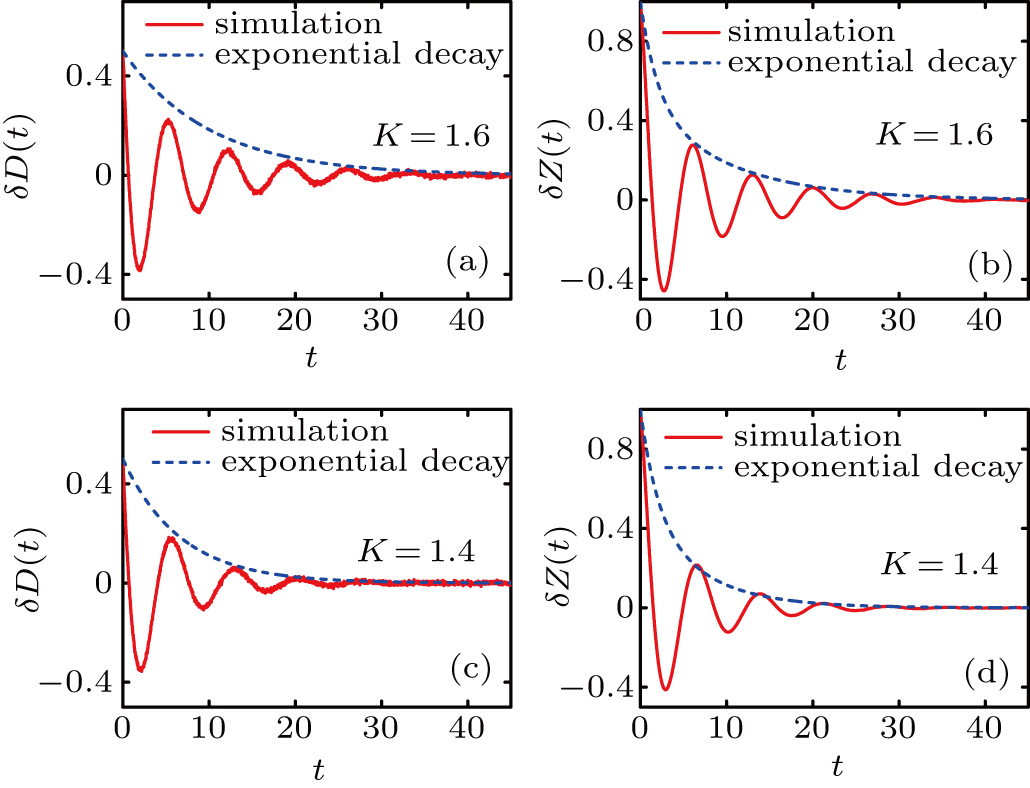
The decay of δ D(t) and δ Z(t) in the in-frequency-weighted case with different K (K < Kc). The solid lines are the direct numerical solutions of Eq. (