Project supported by the National Key Research and Development Program of China (Grant No. 2018YFE0308102), the National Natural Science Foundation of China (Grant Nos. 11735015 and 51771185), the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant No. 17KJB140008), and Jinling Institute of Technology, China (Grant Nos. jit-fhxm-201601 and jit-b-201616).
Project supported by the National Key Research and Development Program of China (Grant No. 2018YFE0308102), the National Natural Science Foundation of China (Grant Nos. 11735015 and 51771185), the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant No. 17KJB140008), and Jinling Institute of Technology, China (Grant Nos. jit-fhxm-201601 and jit-b-201616).
† Corresponding author. E-mail:
Project supported by the National Key Research and Development Program of China (Grant No. 2018YFE0308102), the National Natural Science Foundation of China (Grant Nos. 11735015 and 51771185), the Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant No. 17KJB140008), and Jinling Institute of Technology, China (Grant Nos. jit-fhxm-201601 and jit-b-201616).
The carbon diffusivity in tungsten is one fundamental and essential factor in the application of tungsten as plasma-facing materials for fusion reactors and substrates for diamond growth. However, data on this are quite scarce and largely scattered. We perform a series of first-principles calculations to predict the diffusion parameters of carbon in tungsten, and evaluate the effect of temperature on them by introducing lattice expansion and phonon vibration. The carbon atom prefers to occupy octahedral interstitial site rather than tetrahedral interstitial site, and the minimum energy path for its diffusion goes through a tetrahedral site. The temperature has little effect on the pre-exponential factor but a marked effect on the activation energy, which linearly increases with the temperature. Our predicted results are well consistent with the experimental data obtained at high temperature (>1800 K) but significantly larger than the experimental results at low temperature (<1800 K).
Diffusion of carbon atoms in metals is of great scientific and technological interests because it is closely related to many important phenomena in materials science.[1–5] A typical example is that the diffusion of carbon controls kinetics of carbonization of parent metal and alloy elements.[3,4] In addition, diffusion of impurity carbon significantly affects its surfaces and grain boundary segregation properties, which in turn leads to changing mechanical properties of metals.[5,6] Recently, carbon behavior in tungsten has attracted a great deal of attention. Firstly, both tungsten and carbon have been selected as the plasma-facing materials (PFM) in the international thermonuclear experimental reactor (ITER).[7,8] During operation of this device, carbon will be inevitably introduced in tungsten and thus become one of the most frequent impurity atoms in it. Secondly, the drawback of tungsten as PFM in future fusion reactors is its high ductile-to-brittle transition temperature (DBTT) and therefore high brittleness at the operation temperature.[9] The introduce of fine and uniform dispersion of carbides in tungsten is an effective way to improve ductility by lowering DBTT.[9,10] In addition to the application in fusion reactors, tungsten has also been considered as the best substrates for diamond growth.[11] The diffusion behavior of carbon in tungsten substrates can affect the nucleation and surface morphology of diamond. For these reasons, it is very important to know the diffusion behavior of carbon in tungsten.
The diffusion of carbon in tungsten has been thoroughly investigated experimentally for over 50 years.[12–20] However, data on this are still scarce and, more importantly, the values of diffusion parameters obtained are different. As shown in Table
| Table 1. The pre-exponential factors and activation energies obtained by experimental measurements and first-principles calculations . |
The diffusivity of interstitial solute atoms in solid solutions can be expressed as[34]
 |
One method is based on Eyring’s theory of the activated complex, involving time-consuming calculations of vibrational frequencies,[35–38] which is denoted by hTST. In this method, the jump rate (denoted by ΓhTST) is given by
 |
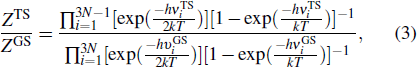 |
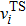
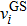
 |
 |
The temperature effect is taken into account by considering the thermal expansion and phonon vibration. Lu et al.[40] have proposed an equation to describe the lattice thermal expansion of tungsten, whose calculated results are fully consistent with the experimental data reported. Therefore, this equation can be used to correlate the temperature with the lattice parameter value. Similarly to previous works,[25,28,29] the relevant lattice constant (aT) at temperature T can be calculated by multiplying the DFT-optimized lattice constant a0 at 0 K by the ratio 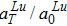
 |
 |
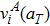
 |
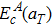
The present calculations are performed by the Vienna ab-initio simulation package (VASP) code based on density functional theory (DFT). The projector augmented wave (PAW) pseudo-potentials are used to describe interactions between ions and valence electrons.[41] For the exchange–correlation potential, the generalized gradient approximation as parameterized by Perdew–Wang (PW91) is used.[42,43] A supercell containing 128 lattice points (4 × 4 × 4) is used. Throughout the calculations, the atomic position is allowed to relax while the shape and volume of the supercell are fixed. The plane wave cutoff of 500 eV and k-point grid density of 5 × 5 × 5, generated by the Monkhorst–Pack method,[44] are employed, which give a convergence of the total energy within 0.001 eV per atom. The structural optimization is truncated when forces on all atoms in the supercell are less than 0.01 eV/Å. Lattice vibrations are calculated using the harmonic approximation and the frozen phonon approach. Similar to the previous work,[28] localized vibrations of the interstitial carbon atom and its neighboring tungsten atoms are assumed to be decoupled from vibrations of other metal atoms, i.e., only the interstitial carbon atom and its neighboring tungsten atoms are allowed to vibrate.
The calculated lattice constant of the tungsten at 0 K is 3.177 Å, which agrees well with the previous calculation results[29–31,33] and is slightly larger than the experimental value (3.165 Å[45]). Using Eq. (
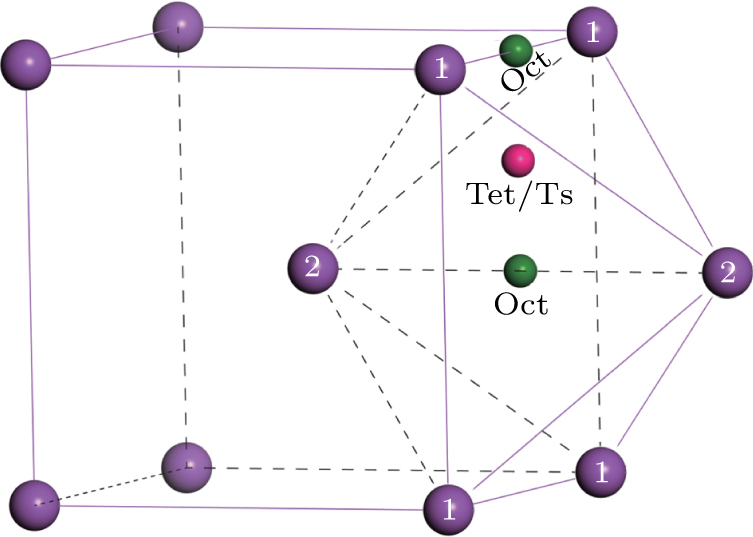
To verify the accuracy of our calculations, the solution and diffusion properties of interstitial carbon in tungsten at 0 K are calculated. Being small enough, carbon will occupy interstitial sites in bcc metal. Two possible interstitial sites, i.e. tetrahedral (Tet) and octahedral (Oct) sites, are considered. The formation energy is calculated by Ef = EWC – EW – EC, where EWC is the total energy of the tungsten lattice with a carbon atom at interstitial site, EW is the total energy of tungsten perfect supercell, and EC is the energy of carbon isolated. Using this equation, the formation energies of carbon in tetrahedral and octahedral sites are calculated to be −4.45 eV and −5.92 eV, respectively. This means that the carbon atom prefers to occupy octahedral interstitial site rather than tetrahedral interstitial site. For seeking the saddle point in the process of the carbon atom migration, the nudged elastic band (NEB) method is utilized. The interpolation points of the system are set 5 to construct a minimum energy path. According to our calculation, the minimum energy path for the interstitial carbon diffusion is found directly through a Tet, i.e., the path Oct→Tet→Oct shown in Fig.
The temperature effect on the activation energy can be evaluated by substituting Eq. (
 |
 |
 |
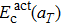
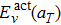

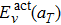
| Table 2. The carbon interstitial atom induced lattice stress (in GPa) in bcc tungsten. The compressive stress is negative and the tensile stress is positive. . |
Similar to the case of hydrogen in tungsten,[28,46] the dependence of 
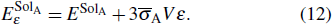 |
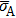
 |
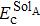
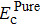
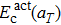
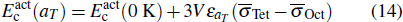 |
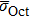
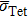
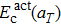
Lattice expansion in general leads to a softening of vibrational modes, which in turn affects the vibration free energy and the partition functions (see section 
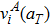


Using the two distinct methods of the calculation of the jump rate described in Section 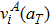
 | Fig. 5. The predicted diffusivity of carbon in tungsten with and without the temperature effect and the corresponding pre-exponential factors and activation energies. |
The agreement with experimental results is an extremely important criterion to verify theoretical predictions. For the interstitial diffusion of light elements in metals, the diffusivity data obtained at high temperatures are usually believed to be more reliable since they are likely less influenced by both surface and trapping effects. However, it is difficult to experimentally determine the temperature range without trapping effects due to the lack of the benchmarks. A comparison of experimental and theoretical data may hopefully solve this problem. Figures
We have performed a series of first-principles calculations to predict the carbon diffusion parameters in tungsten, namely, pre-exponential factor, activation energy, and diffusivity. The temperature effects on these diffusion parameters are evaluated by considering the lattice expansion and phonon vibration. It is found that the carbon atom prefers to occupy octahedral interstitial site rather than tetrahedral interstitial site, and the minimum energy path for its diffusion goes through a tetrahedral site. The predicted pre-exponential factor is around 3 × 10−7 m2/s over the investigated temperature range of 300–2700 K, which is not affected by temperature and consistent with the experimental results. The predicted activation energies linearly increase from 1.47 eV to 1.67 eV at temperatures 300–2700 K, which are consistent with the experimental data obtained at high temperatures (>1800 K) but much lower than those obtained at low temperatures (<1800 K). The temperature effect on the carbon diffusivity in tungsten is not significant because the change of activation energies with temperature contributes less to the diffusion coefficient at high temperatures. Similarly to the activation energies, our predicted diffusivity data are very good consistent with the high-temperature experimental values (>1800 K) but larger than the low-temperature experimental results.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] |