† Corresponding author. E-mail:
The principle of dual-energy x-ray grating phase-contrast imaging (DEPCI) is clarified by using the theory of x-ray interference and Fresnel diffraction. A new method of retrieving phase from the two interferograms is proposed for DEPCI, and its feasibility is verified via simulation. Finally, the proposed method applied to DEPCI experiment demonstrates the effectiveness of the method. This paper lays the theoretical foundation for performance optimization of DEPCI and the further integration of DEPCI and computed tomography.
Traditional x-ray imaging is based on the varied absorption of x-rays by the different materials in the object of interest. While it is widely used in medical imaging and industrial non-destructive testing, the poor absorption of x-rays by soft tissues in organisms, such as in ligaments and tumors, results in poor absorption contrast. Fortunately, phase contrast imaging can compensate for this deficiency. Absorption and phase contrast of x-rays result from the attenuation of their amplitudes and shifts of their phases, respectively. Upon exposure to hard x-rays (0.01 nm–0.1 nm), the shift of phase is at least three orders of magnitude higher than that caused by the attenuation of amplitude. Even for thin specimens, the presence of light elements can cause an obvious phase contrast. This means that phase-contrast imaging can achieve more detailed imaging of specimens that are unrecognizable when imaged by absorption contrast. Therefore, for objects composed of light elements, detecting a shift of phase is easier and more efficient than detecting an attenuation of the amplitudes.
Since the late twentieth century, various forms of x-ray phase-contrast imaging have gradually been developed. Although the crystal interferometer[1] and free-space propagation techniques[2] yield ideal results for specific problems, none of them has found wide applications in medical or industrial area, which typically require the use of a laboratory x-ray source, a large imaging field of view and good imaging system stability. Grating phase contrast imaging represented by the Talbot–Lau interferometer[3] can solve the above problems. However, its corresponding method of retrieving the phase, called “phase stepping”, requires the multi-stepping of the grating in its single period with the sample existing, which will bring two limitations. The first limitation is that the objects need to be exposed to x-rays at least three times (generally 5–11 times), prolonging the data acquisition time, and causing the ionizing x-ray radiation to be absorbed excessively, which may leads organisms to suffer from genetic disease or even carcinosis. The second limitation is that the grating must be moved in micron-sized steps, thus requiring a high-level mechanical precision. The reduction of radiation doses during x-ray imaging and the number of phase steps have been a focus of recent investigation.
Zhu et al.[4] proposed a method of projecting objects forward and backward without a stepping device for grating in 2010. Their method reduces the exposure time but requires high grating uniformity. Liu et al.[5] proposed a two-step method by combining the analyzer grating with fluorescent screen in 2010. However, a stepping device was still required. In 2017, for free-space propagation techniques, Wang et al.[6] proposed an excellent method, which is expected to be used in zero-step grating phase contrast imaging. In 2010, Kottler et al.[7] applied the dual-energy modality of the traditional x-ray imaging to the Talbot–Lau interferometer, thus enabling the phase contrast imaging to discriminate the information about the specific material composition. With this background, Rong[8] et al. proposed the dual-energy x-ray grating phase contrast imaging (DEPCI) with a dual-energy analyzer grating[9] in 2018. With omitting the stepping device, only the working energy in the DEPCI system needs to be changed once in the imaging experiment. However, accurate theoretical calculations have not yet been made for this method of retrieving the phase. In this paper, the theoretical framework of DEPCI is first elaborated. Furthermore, a new method of retrieving the phase is proposed. The relevant simulation and experimental results demonstrate the effectiveness of this method.
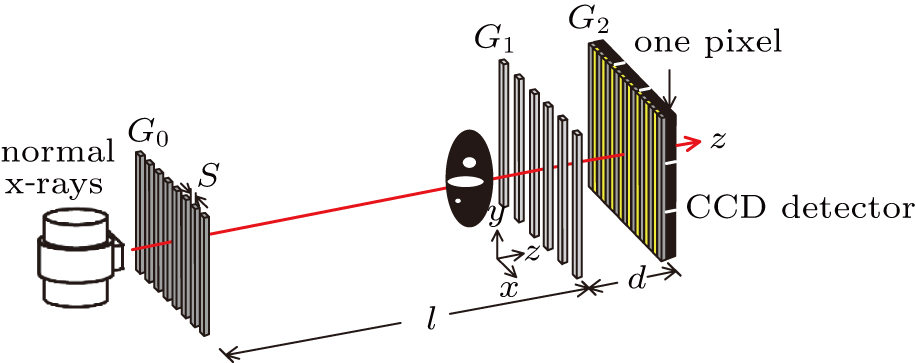
As shown in Fig.
The source grating G0 divides the normal x-rays into several slit x-rays. In particular, x-rays within the same slit are coherent. The Talbot effect occurs when the spatial coherence length 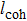
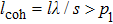
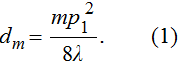 |
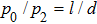
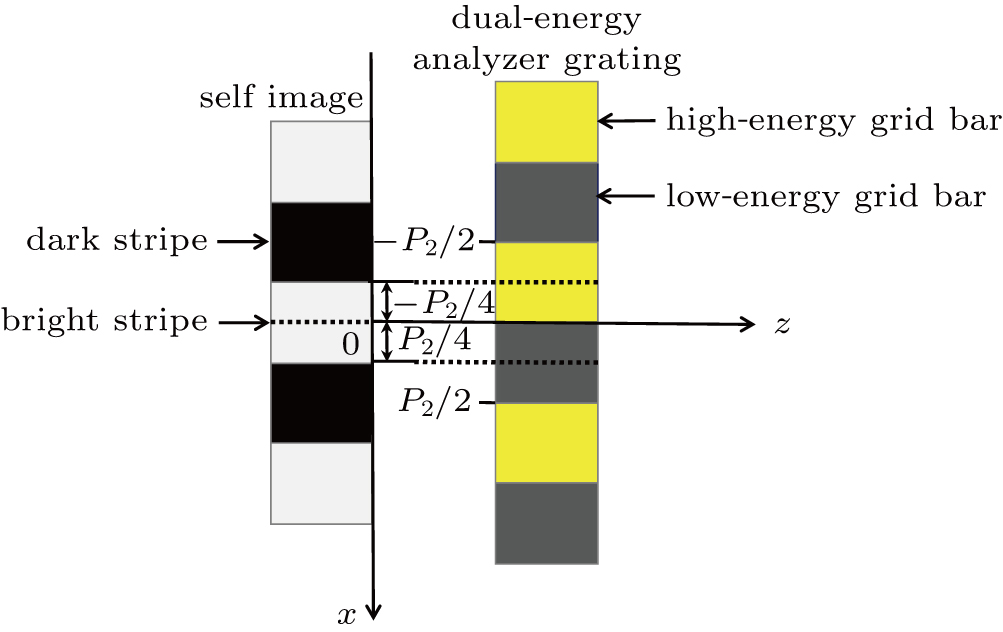
However, the period of a self-image is typically a few microns, which is smaller than the minimum resolution of CCD detector. Therefore, a dual-energy analyzer grating G2 is overlapped with the self-image at an angle to form large-period moirè fringes. The coordinates of the self-image and dual-energy analyzer grating are shown in Fig.
The alternating response of the high- and low-energy grid bars of G2 to high- and low-energy x-rays are equivalent to a step in the traditional grating of Talbot–Lau interferometer. Therefore, it is necessary to ensure that the Talbot distance and fringe distribution of the self-images in high- and low-energy x-rays are consistent with each other. According to Eq. (

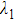
 |
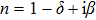
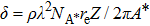
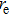
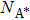
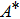
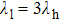

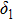
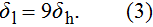 |
Assuming that 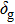
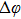
 |
In DEPCI, G1 is designed to shift the phase of the low-energy x-rays by π. Correspondingly, G1 shifts the phase of the low-energy x-rays by 3π. The self-images of the π and 3π phase grating are consistently distributed.[14]
As shown in Fig. 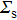
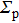
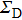

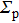
The complex wave-front amplitude propagating from the point source a of 
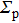
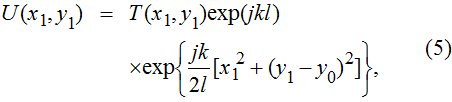 |

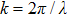
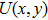
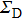
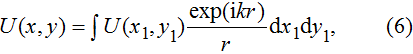 |
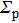
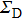
 |
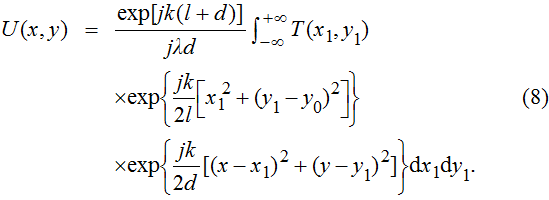 |
 |
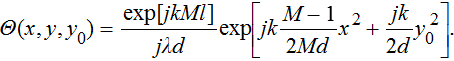 |
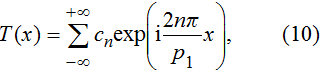 |
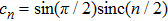
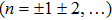
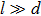
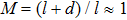
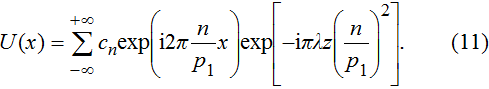 |
When a sample is placed in the DEPCI system, x-rays undergo amplitude (A(x)) attenuation and phase 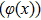
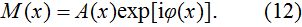 |
The phase grating G1 splits the x-rays, producing a shear expressed as 
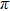
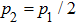
 |
For hard x-rays in light-element objects, the shear quantity of the amplitude attenuation is quite small, so we can reasonably take the following approximation: 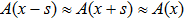
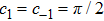
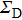
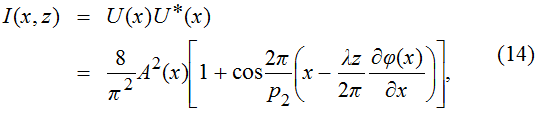 |
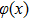
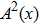
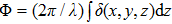
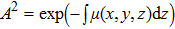
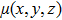
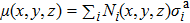
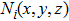
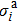
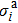
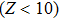
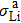
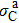
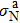
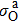
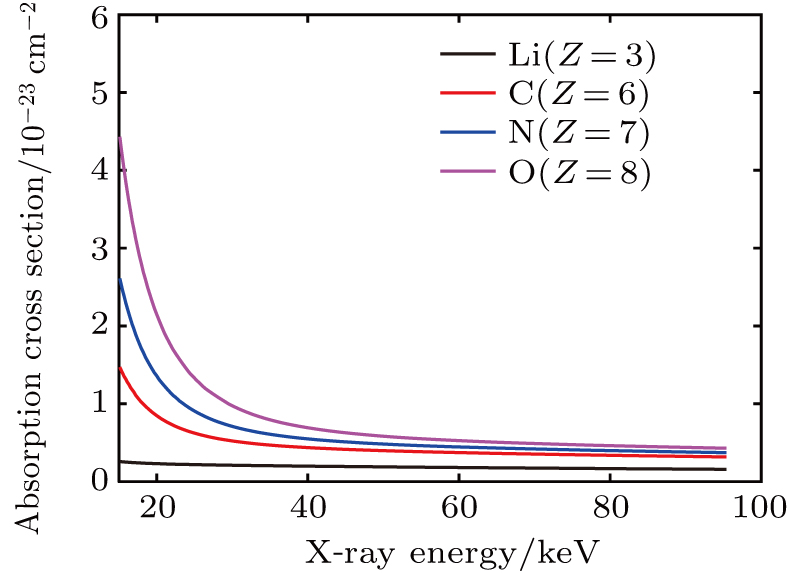
It should be noted that as the x-ray energy increases, the values of the absorption cross sections 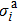

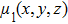
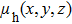
As shown in Fig.
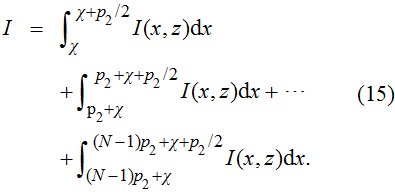 |
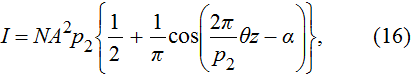 |
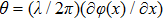
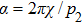
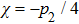
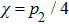
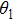
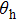
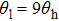
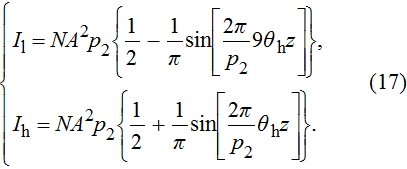 |
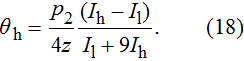 |
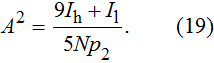 |
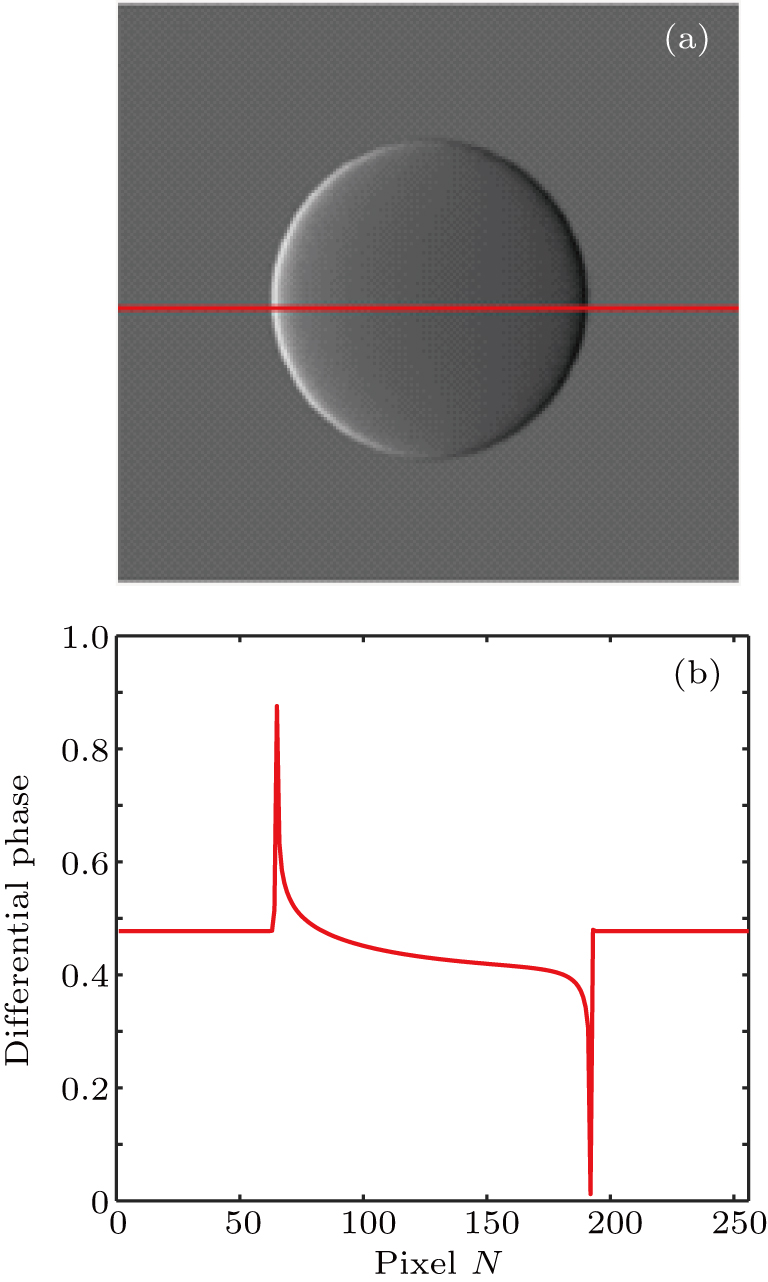
To demonstrate the feasibility of the proposed method, we simulated the imaging procedure of DEPCI with a PMMA-formvar ball. The ball had an average density 
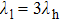
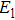
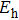
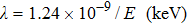
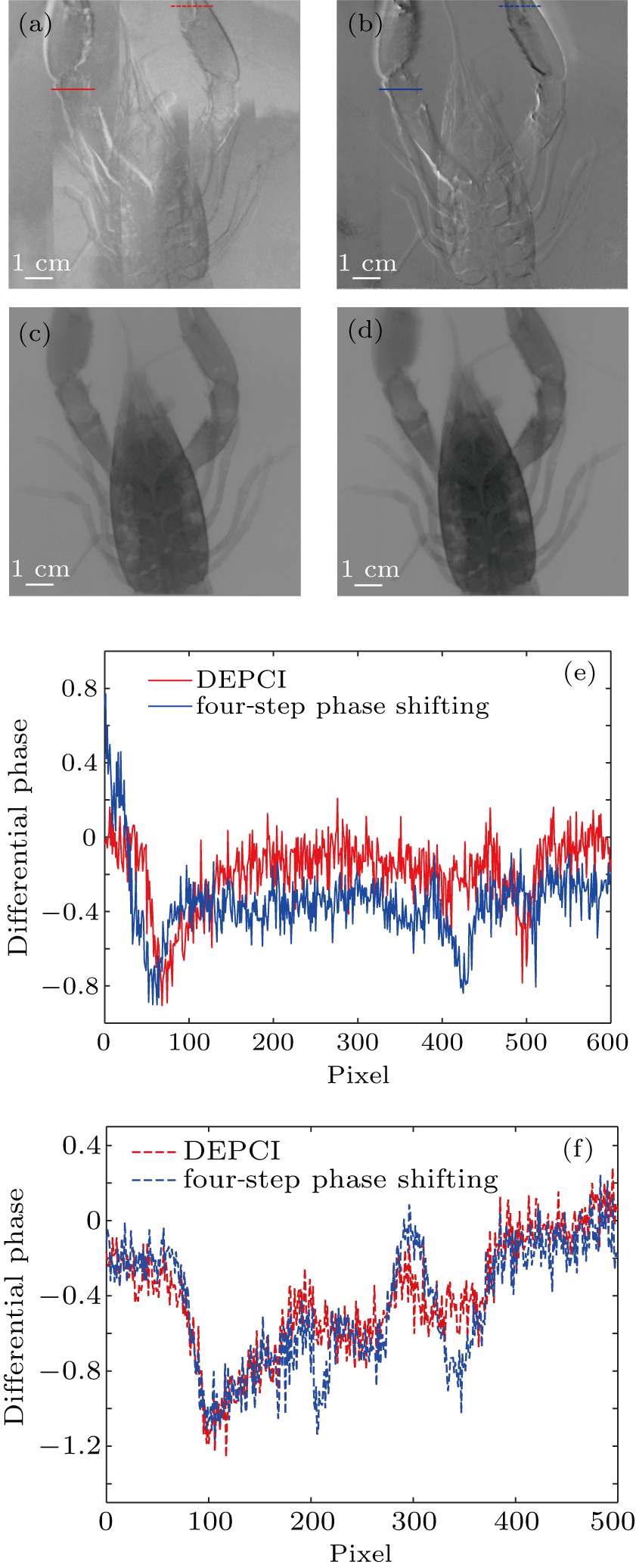
As shown in Fig.
During the DEPCI experiment, the focal spot size of the conventional tungsten target x-ray source was 1 mm×0.8 mm. An x-ray energy radiation detector was used to calibrate the energy of x-rays. Since the required exposure decreased as the difference between the two energies increased,[23] the wide-spectrum x-rays with the central photon energy of 20 keV and 60 keV were selected as the values of low and high energies, respectively. The tube current was also adjustable from 2 mA to 4 mA. The duty ratios of G0 and G1 were 1:3 and 1:2, respectively. The following parameters were used in the simulation: 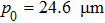
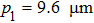
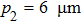
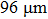
From the extracted information shown in Fig.
However, the DEPCI has a disadvantage that it cannot be used for dark field imaging. In Ref. [24], equation (
In this paper, we present theoretical calculations for DEPCI. Furthermore, by exploiting the intrinsic phase change and characteristics of linear absorption coefficient of low- and high-energy x-rays, a method of retrieving the phase for DEPCI is found. The results of simulation and experiment demonstrate that this method is suitable for DEPCI. The phase-contrast image recovered from the two interferograms collected by the DEPCI without moving any device has a similar effect to the phase-contrast image recovered from the four interferograms collected by the Talbot–Lau interferometer by moving the grating four times. Due to the short exposure time, high stability, and computed tomography (CT) compatibility, the DEPCI may become, we believe, a popular method of obtaining the x-ray grating phase contrast imaging.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] |