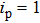† Corresponding author. E-mail:
Project supported by the Thirteenth Five-Year Program for Science and Technology of Education Department of Jilin Province, China (Grant No. JJKH20191007KJ) and the Program for Development of Science and Technology of Siping City, China (Grant No. 2016063).
Micromagnetic simulation is employed to study the gyration motion of magnetic vortices in distinct permalloy nanodisks driven by a spin-polarized current. The critical current density for magnetic vortex gyration, eigenfrequency, trajectory, velocity and the time for a magnetic vortex to obtain the steady gyration are analyzed. Simulation results reveal that the magnetic vortices in larger and thinner nanodisks can achieve a lower-frequency gyration at a lower current density in a shorter time. However, the magnetic vortices in thicker nanodisks need a higher current density and longer time to attain steady gyration but with a higher eigenfrequency. We also find that the point-contact position exerts different influences on these parameters in different nanodisks, which contributes to the control of the magnetic vortex gyration. The conclusions of this paper can serve as a theoretical basis for designing nano-oscillators and microwave frequency modulators.
Magnetic vortex (MV) often exists in nanodisks made of soft ferromagnetic materials, which can be characterized by an out-of-plane polarity and an in-plane chirality.[1,2] The MV has received much attention for its technological applications in spin-transfer-torque magnetic random access memories, logical devices, and nano-oscillators because of its unique dynamical behaviors.[3–10] In order to apply MV to new spintronic devices, the key point is to control the dynamic properties of MV such as the polarity reversal, chirality reversal, and gyration.[4,11–19] Recently, we investigated the polarity reversal mediated by a spin-polarized current in a confined geometry, finding that not only the MV can be easier triggered but also the polarity can be reversed with a lower current density and using less time if the point-contact is not designed in the nanodisk center.[20,21] Furthermore, our research found that the position and the size of point-contact can control the eigenfrequency of MV gyration.[15,22,23] Taking into account the previous studies and considering the better application of MV,[24] we particularly focus on the MV gyration in permalloy (Py) nanodisks with different sizes in this paper and investigate the effects of the point-contact position on MV gyration, including the critical current density of MV gyration, eigenfrequency, trajectory, velocity, and the time for a magnetic vortex to obtain the steady gyration.
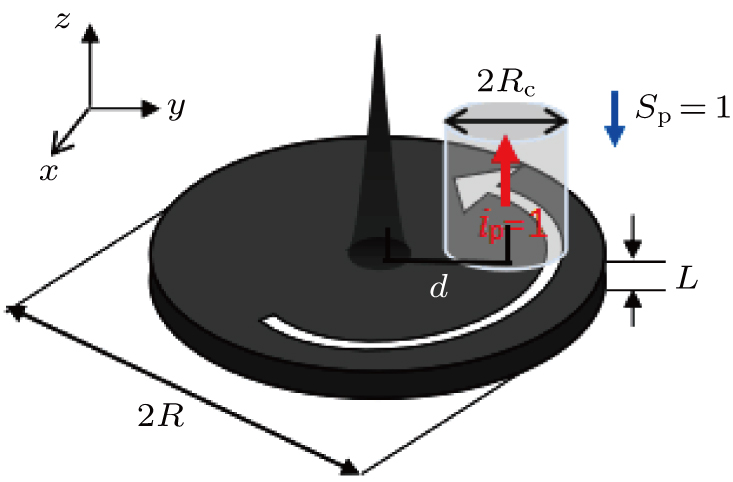
In this work, we pay our attention to the MV gyration in Py nanodisks with different sizes as shown in Fig. 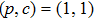
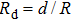
Magnetization simulation calculation is performed by OOMMF based on Landau–Lifshitz–Gilbert (LLG) equation with spin-transfer-torque (STT) and Oersted field induced by the current,[18,19,25]
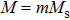
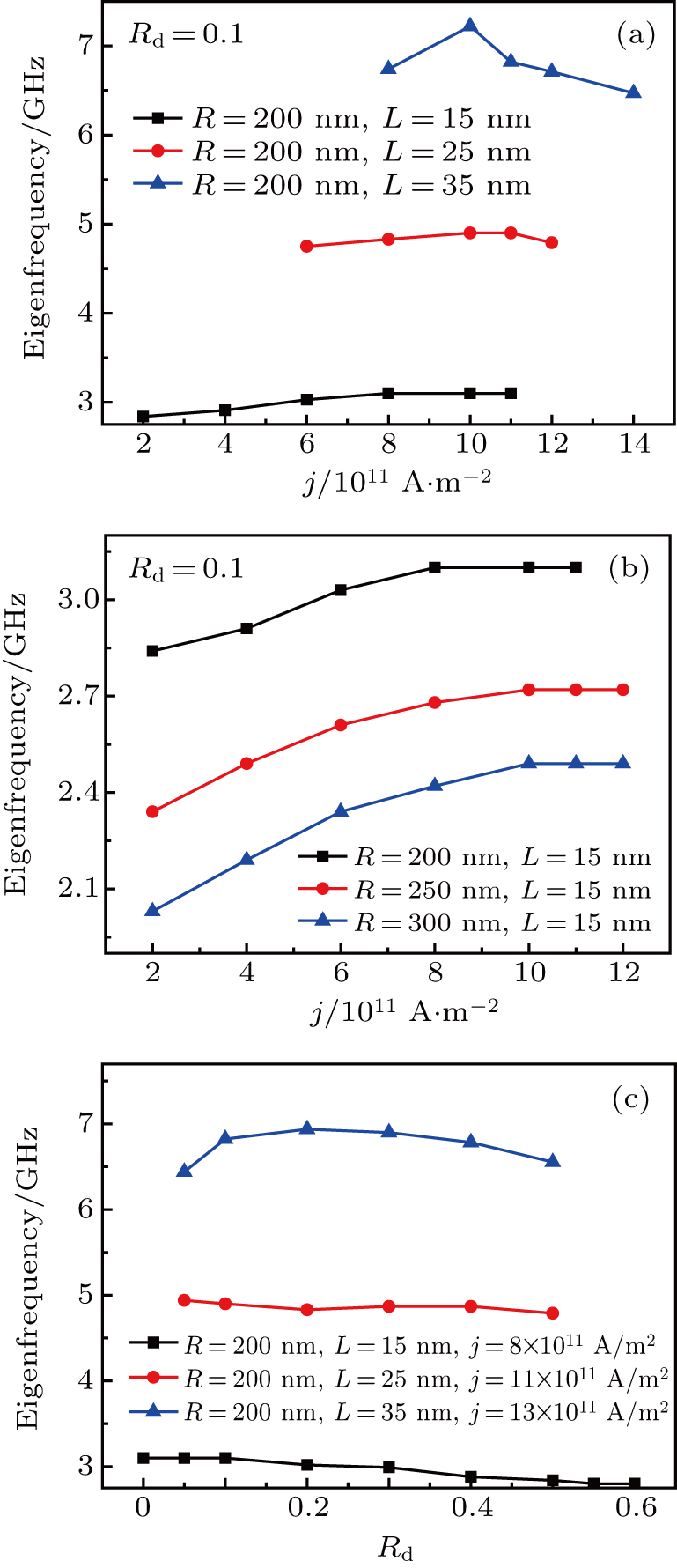
Firstly, we should confirm the minimum value of the current density that can trigger the MV gyration in different nanodisks, and this value is defined as critical current density jg. Figure 
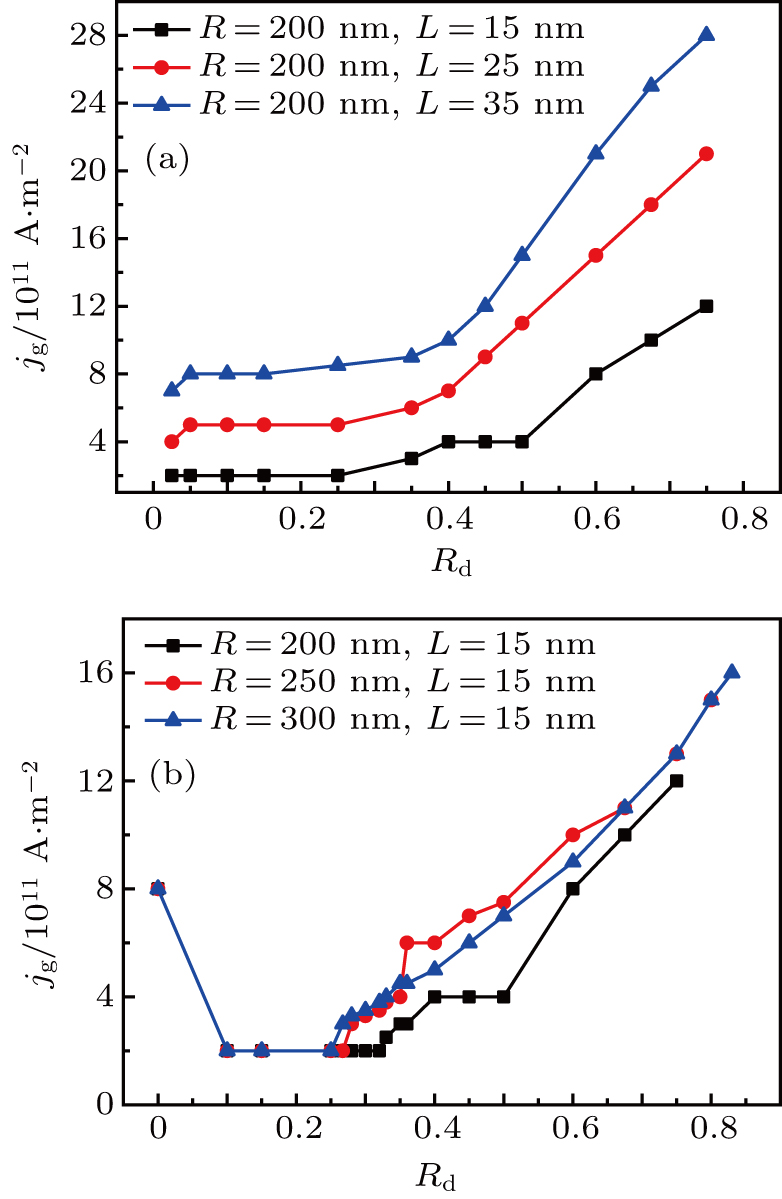 | Fig. 2. Plots of critical current density of gyration jg versus Rd (a) for nanodisks with the same R and different values of L, and (b) for the nanodisks with the same L and different values of R. |
The eigenfrequency is a vital parameter of the MV application for nano-oscillators and modulators. We obtain the eigenfrequency of MV gyration from fast Fourier transform based on magnetization 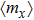
The MV trajectory and velocity are other two important dynamic parameters of gyration. The trajectory is also different in thick and thin disk at Rd=0.1 as shown in Figs.
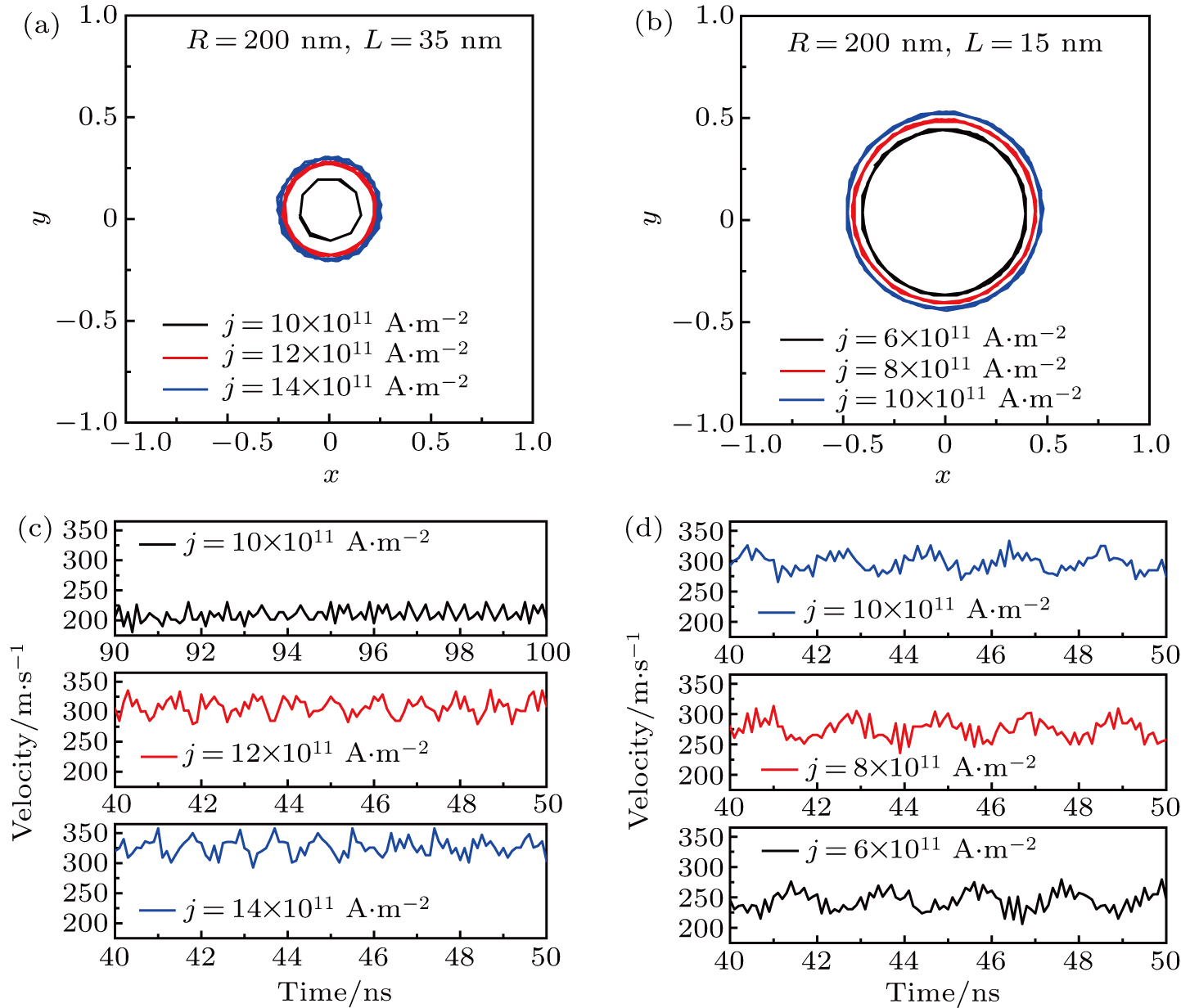 | Fig. 4. Steady gyration orbits of magnetic vortex in (a) thick and (b) thin nanodisk. Steady gyration velocities of magnetic vortex in (c) thick and (d) thin nanodisk. |
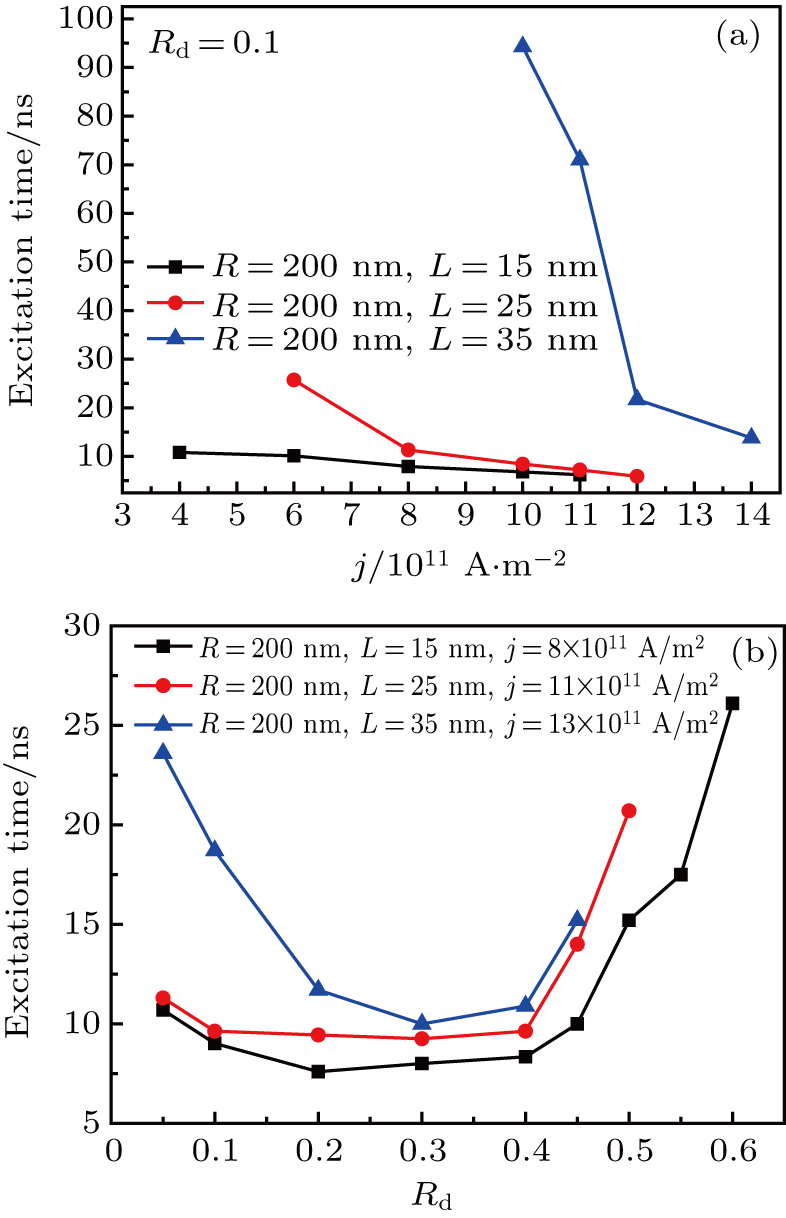
Besides the different orbit radii and steady velocities, another parameter should be paid more attention to, which is the excitation time and it is defined the time interval between the start of current injection and the MV reaching the steady gyration. We plot excitation time as a function of j and Rd in Fig.
In this work, the gyration of the magnetic vortex in different permalloy nanodisks are analyzed, including the critical current density of triggering magnetic vortex gyration, eigenfrequency, trajectory, velocity, and excitation time. It is observed that the magnetic vortices in larger and thinner nanodisks can obtain gyration at a lower current density and shorter excitation time, whereas they have low eigenfrequencies. On the contrary, the magnetic vortices in thicker nanodisks need higher current density and longer time to attain steady gyration but have larger eigenfrequencies. Furthermore, the simulation results demonstrate that the point-contact position of spin-polarized current has great effects on these parameters and therefore, the magnetic vortex gyration can be controlled by the point-contact position. The calculation results and analyses in this work can open the way for designing magnetic vortex nano-oscillators and modulators.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] |