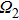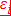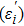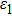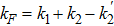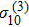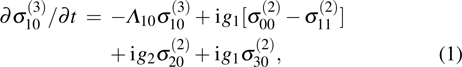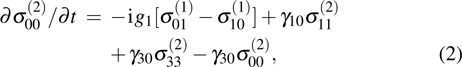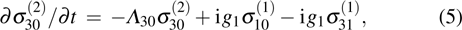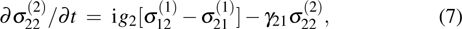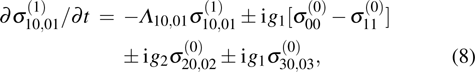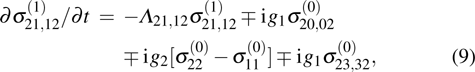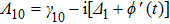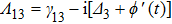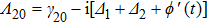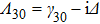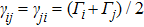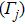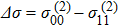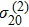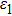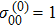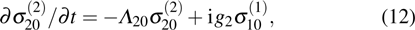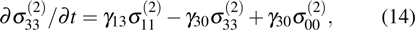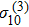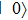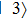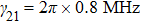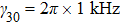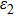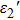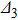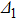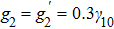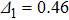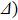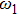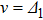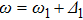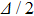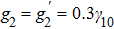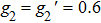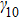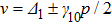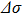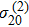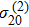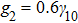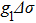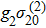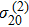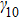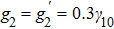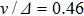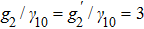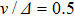Dynamic and inner-dressing control of four-wave mixing in periodically-driven atomic system
Institute of Physics, Xi’an University, Xi’an 710065, China
† Corresponding author. E-mail:
liyynxcn@aliyun.com
1. IntroductionThe suppression and enhancement of four-wave-mixing (FWM) process in electromagnetically induced transparency (EIT) windows[1–8] can be implemented in many multi-level systems, such as ladder-type,[2,9,10] Y-type,[8] and double lambda-type[4–6,11–13] level configurations. In a ladder-type system with hyperfine ground states, the magnitude of FWM signal is found to be dependent on the transition route, and dominantly related to the residual two-photon coherence according to the degree of optical pumping to the other ground state.[9] While these features in the cycling transition are dramatically influenced by ladder-type and V-type two-photon coherence components, respectively.[9] Highly efficient FWM and six-wave mixing (SWM) signals coexisting in EIT windows were reported in an open four-level Y-type atomic system, in which the interplay between these two nonlinear processes is due to three- and five-photon destructive interferences.[8] Recently, in a backward double-lambda system, the conversion efficient in cold rubidium atoms was observed to be 63%, and the conversion efficient was predicted to be 96% by using a medium with a large optical depth.[13]
The control of FWM process can be achieved by changing several parameters of the fields applied to the system, e.g., the detuning and the strengths,[8,14] the relative phases,[15] and the pulse dynamics.[16] This control of FWM process can be applied to the quantum entanglement,[17] the fabrication of scalable multimode quantum resources,[18] and the enhancement of bright-seeded SU(1,1) interferometer.[19,20] In the present work, we consider a reverse Y-type atomic system driven by one probe and two coupling fields. The probe field is periodically modulated by a phase function. The two coupling fields are involved in both FWM and dressing process, thus we term the coupling fields inner-dressing fields hereafter. We will show that the FWM process can be successfully controlled by selecting different dynamic parameters of the probe field, and strengths of the inner-dressing fields. We will also show that the controllable FWM process is dominantly influenced by the evolution of atomic population difference and two-photon coherence. This type of dynamic and inner-dressing control of FWM can be probably used in optical information processing.
2. Theoretical modelA reverse Y-type four-level atomic system is shown in Fig. 1(a), where
 and
and
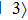 are selected as hyperfine levels with a splitting difference Δ;
are selected as hyperfine levels with a splitting difference Δ;
 and
and
 are the intermediate and the excited states of the atom, respectively. Beams diagram is shown in Fig. 1(b), where beam 1 represents a weak probe field
are the intermediate and the excited states of the atom, respectively. Beams diagram is shown in Fig. 1(b), where beam 1 represents a weak probe field
 , while beams 2 and
, while beams 2 and
 propagating with a small angle difference (∼0.5°) represent strong inner-dressing fields
propagating with a small angle difference (∼0.5°) represent strong inner-dressing fields
 and
and
 , respectively. The transition frequency of
, respectively. The transition frequency of
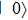 –
–
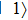 ,
,
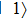 –
–
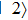 , and
, and
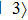 –
–
 are
are
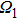 ,
,
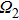 , and
, and
 respectively. The frequency, the detuning, the Rabi frequency and the wave vector of the field
respectively. The frequency, the detuning, the Rabi frequency and the wave vector of the field
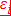
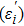 are denoted as
are denoted as
 ,
,
 , gi
, gi
 , and
, and

 respectively. The
respectively. The
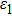 is assumed to be periodically modulated by a phase function
is assumed to be periodically modulated by a phase function
 , where A and ν are the modulation amplitude and frequency, respectively.[21] If the phase-matching condition
, where A and ν are the modulation amplitude and frequency, respectively.[21] If the phase-matching condition
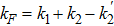 is satisfied, the FWM signal propagating in the direction almost opposite to the beam
is satisfied, the FWM signal propagating in the direction almost opposite to the beam
 can be generated.
can be generated.
The FWM signal is governed by the third-order density matrix elements
 and
and
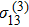 . Considering that
. Considering that
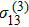 exhibits almost the same feature as
exhibits almost the same feature as
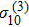 , we calculate only the density matrix element
, we calculate only the density matrix element
 by using the following coupling equations:
by using the following coupling equations:
where the complex detunings
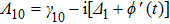
,
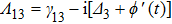
,
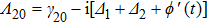
,

,
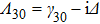
,

with

(

); the decay rate from level

to

(

) is defined as
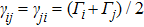
with

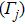
being the decay rates of level

(

).
To obtain the above coupling equations, we assume that
 and
and
 . It is obvious that the modification of
. It is obvious that the modification of
 is mainly influenced by the evolution of population difference
is mainly influenced by the evolution of population difference
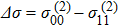 , two-photon coherences
, two-photon coherences
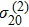 and
and
 . To solve these coupling equations, Fourier expansion of the field
. To solve these coupling equations, Fourier expansion of the field
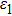 is usually used to find the resonant components involved in the coupling of relative transitions.[19] However, this method is cumbersome and incomplete for solving the dynamic and inner-dressing problem. In the following discussion, we numerically solve the above coupling equations by using the algorithm developed in Refs. [21] and [22]
is usually used to find the resonant components involved in the coupling of relative transitions.[19] However, this method is cumbersome and incomplete for solving the dynamic and inner-dressing problem. In the following discussion, we numerically solve the above coupling equations by using the algorithm developed in Refs. [21] and [22]
To simplify the calculation, the atoms are assumed to be initially populated at the ground state
 , i.e.,
, i.e.,
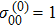 and
and
 (
(
 ), one can obtain immediately
), one can obtain immediately
 . The coupling equations (3)–(6), and (8) are reduced to Eqs. (11)–(14), and (15) respectively:
. The coupling equations (3)–(6), and (8) are reduced to Eqs. (11)–(14), and (15) respectively:
The FWM signal is proportional to the third-order density matrix element
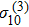 , which can be obtained by numerically solving Eqs. (1), (2), and (11)–(15). In the following, we analyze these numerical results of FWM signals modified by dynamic parameters of the probe field, and the strength of the inner-dressing fields.
, which can be obtained by numerically solving Eqs. (1), (2), and (11)–(15). In the following, we analyze these numerical results of FWM signals modified by dynamic parameters of the probe field, and the strength of the inner-dressing fields.
3. Numerical results and discussionParameters of 85Rb atom corresponding to possible experiments are chosen in our numerical calculation, where 5S1/2 (F = 2), 5S1/2 (F = 3), 5P1/2, and 5D1/2 levels are corresponding to states
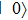 ,
,
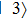 ,
,
 , and
, and
 , respectively. These resonances at the structure are feasible to accomplish a chip-scale setup, which have a great practical importance. At the same time the harmonic phase modulation (frequency deviation) of miniature semiconductor laser (so-called VICSEL) is ordinarily used in practice.[23] The decay rates are
, respectively. These resonances at the structure are feasible to accomplish a chip-scale setup, which have a great practical importance. At the same time the harmonic phase modulation (frequency deviation) of miniature semiconductor laser (so-called VICSEL) is ordinarily used in practice.[23] The decay rates are
 ,
,
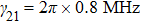 ,
,
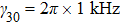 ,
,
 , and
, and
 , respectively. It is assumed that the probe field
, respectively. It is assumed that the probe field
 is always very weak, with taking
is always very weak, with taking
 , the strengths of the inner-dressing fields
, the strengths of the inner-dressing fields
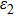 and
and
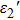 are much greater than that of the probe field. We also assume that the dressing fields are detuned exactly to
are much greater than that of the probe field. We also assume that the dressing fields are detuned exactly to
 transition, i.e.,
transition, i.e.,
 . Considering that
. Considering that
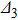 satisfies
satisfies
 (Fig. 1(a)), we are concerned about only the detuning
(Fig. 1(a)), we are concerned about only the detuning
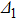 in the following. A typical modulation frequency is usually
in the following. A typical modulation frequency is usually
 , and the FWM lines versus
, and the FWM lines versus
 around
around
 are examined in all cases.
are examined in all cases.
We consider first the case that the strengths of the inner-dressing fields are far less than
 , with taking
, with taking
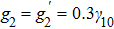 . In this case, both coherent population trapping (CPT)[24] in lambda-type sub-system (
. In this case, both coherent population trapping (CPT)[24] in lambda-type sub-system (
 –
–
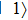 –
–
 ) and EIT in ladder-type sub-system (
) and EIT in ladder-type sub-system (
 –
–
 –
–
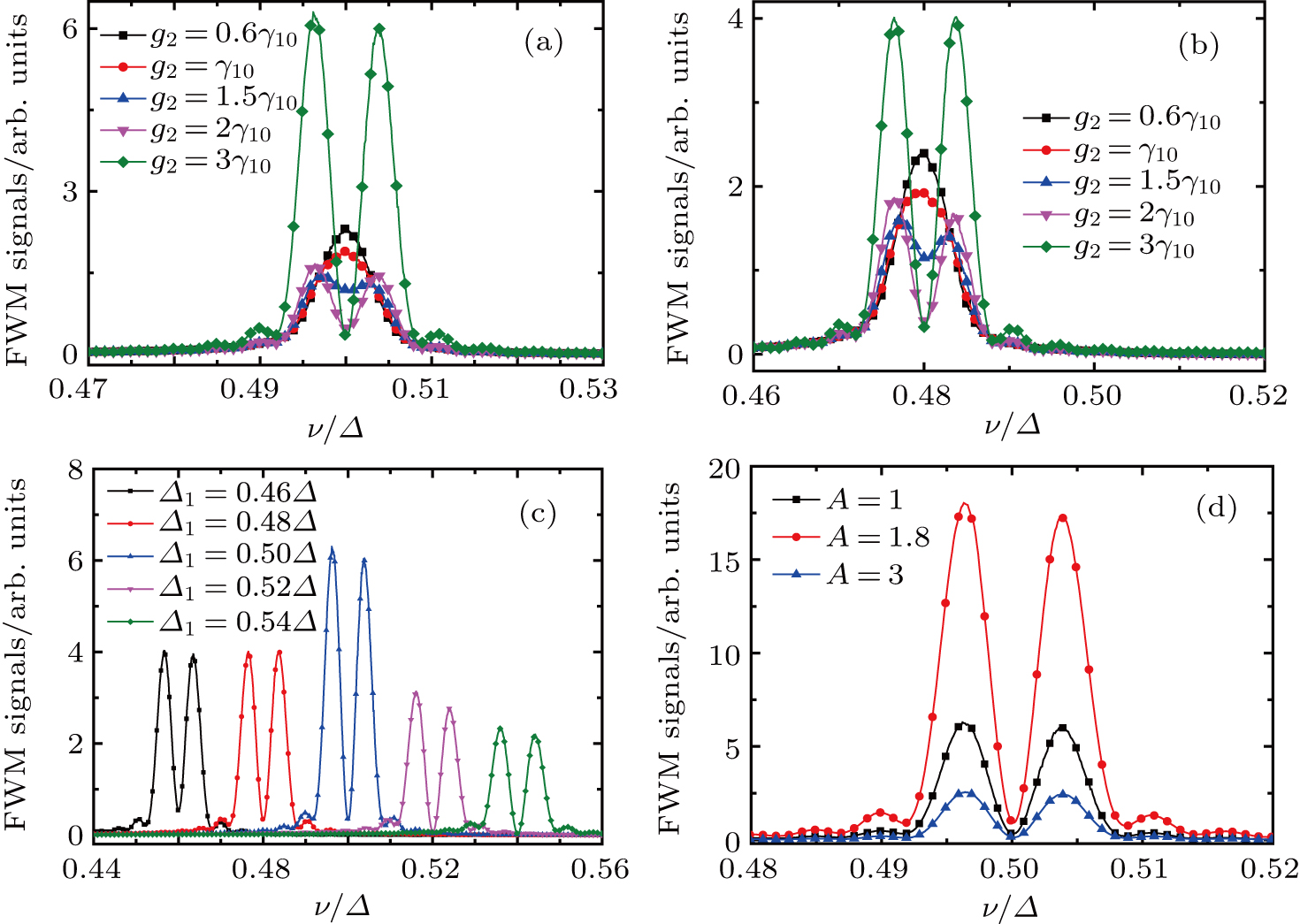
 ) contribute to the formation of a dark state, and FWM signals can transmit in the medium almost without any absorption. The FWM lines are shown in Fig. 2 for the different probe detuning values:
) contribute to the formation of a dark state, and FWM signals can transmit in the medium almost without any absorption. The FWM lines are shown in Fig. 2 for the different probe detuning values:
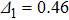 , 0.48, 0.50, 0.52, and 0.54 (in units of
, 0.48, 0.50, 0.52, and 0.54 (in units of
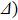 , respectively, where the modulation index A = 1. The peaks of these lines are at the resonant position of
, respectively, where the modulation index A = 1. The peaks of these lines are at the resonant position of
 , i.e., if
, i.e., if
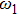 is detuned away from
is detuned away from
 –
–
 transition with a value of
transition with a value of
 , a probe field with a modulation frequency
, a probe field with a modulation frequency
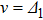 can introduce an enhanced FWM process at
can introduce an enhanced FWM process at
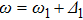 . When the modulation frequency ν is tuned to a fixed value
. When the modulation frequency ν is tuned to a fixed value
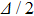 , the peak values of these signals exhibit a damped oscillation behavior (Fig. 3(a)), which indicates that the FWM process can be optimized by appropriately choosing modulation frequency and indices. To verify this, FWM lines are plotted in Fig. 3(b) for A = 0.5, 0.8, 1, 1.95, 2.5, and 3, respectively. It is shown apparently that the FWM signals can be controlled by choosing different modulation parameters of the probe field.
, the peak values of these signals exhibit a damped oscillation behavior (Fig. 3(a)), which indicates that the FWM process can be optimized by appropriately choosing modulation frequency and indices. To verify this, FWM lines are plotted in Fig. 3(b) for A = 0.5, 0.8, 1, 1.95, 2.5, and 3, respectively. It is shown apparently that the FWM signals can be controlled by choosing different modulation parameters of the probe field.
Next, we examine the modulation dependent FWM lines for relative larger inner-dressing strength (Figs. 4(a)–4(d)). In this case, the EIT in ladder-type sub-system (
 –
–
 –
–
 ) dominantly contributes to the formation of a dark state, and FWM signals transmit in the EIT windows. Figure 4(a) and 4(b) show FWM lines for the inner-dressing strengths
) dominantly contributes to the formation of a dark state, and FWM signals transmit in the EIT windows. Figure 4(a) and 4(b) show FWM lines for the inner-dressing strengths
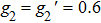 , 1, 1.5, 2, and 3 (in
, 1, 1.5, 2, and 3 (in
 units), respectively, where the modulation index A = 1, and the probe detuning for Figs. 4(a) and 4(b) are
units), respectively, where the modulation index A = 1, and the probe detuning for Figs. 4(a) and 4(b) are
 and 0.48 (in units of
and 0.48 (in units of
 ), respectively. It can be found that an increasing dressing intensity can suppress FWM signals at the resonant frequency of
), respectively. It can be found that an increasing dressing intensity can suppress FWM signals at the resonant frequency of
 . As the dressing strength becomes greater than
. As the dressing strength becomes greater than
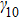 , a largely suppression of FWM signal happens at
, a largely suppression of FWM signal happens at
 , and several enhanced peaks can be observed at
, and several enhanced peaks can be observed at
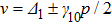 (p = 1, 2, 3, …). As shown in Fig. 4(c), this type of suppression and enhancement of FWM signals can persist for different probe detuning values:
(p = 1, 2, 3, …). As shown in Fig. 4(c), this type of suppression and enhancement of FWM signals can persist for different probe detuning values:
 , 0.48, 0.50, 0.52, and 0.54 (in units of
, 0.48, 0.50, 0.52, and 0.54 (in units of
 ). One can find that the red detuning of the probe field can introduce a larger suppression of FWM signals when the resonant condition
). One can find that the red detuning of the probe field can introduce a larger suppression of FWM signals when the resonant condition
 is satisfied. The modulation index A can also dramatically modify FWM signals in a strong coupling regime (Fig. 4(d)). The greater the peak amplitude, the larger the suppression at the resonant position will be. We believe that this suppression of FWM signals results dominantly from destructive interference between two channels induced by inner-dressing fields,[14] while the enhancement of FWM signals is induced by both dynamic parameters of the probe field and the strong inner-dressing effect.
is satisfied. The modulation index A can also dramatically modify FWM signals in a strong coupling regime (Fig. 4(d)). The greater the peak amplitude, the larger the suppression at the resonant position will be. We believe that this suppression of FWM signals results dominantly from destructive interference between two channels induced by inner-dressing fields,[14] while the enhancement of FWM signals is induced by both dynamic parameters of the probe field and the strong inner-dressing effect.
The controllable FWM signals can be explained by analysing the evolution of atomic level population difference and two-photon coherences. As stated, this evolution of FWM signals is mainly influenced by population difference
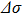 , two-photon coherences
, two-photon coherences
 and
and
 . However,
. However,
 is of third order and less than
is of third order and less than
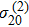 in our calculation, thus the modification of FWM process is influenced dominantly by
in our calculation, thus the modification of FWM process is influenced dominantly by
 and
and
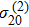 . An increasing coupling intensity will suppress the FWM signals at resonant position, while an enhanced contribution induced by the population change can counteract part of the suppression, e.g., the peak amplitude for
. An increasing coupling intensity will suppress the FWM signals at resonant position, while an enhanced contribution induced by the population change can counteract part of the suppression, e.g., the peak amplitude for
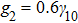 is larger than that for
is larger than that for
 .
.
As the dressing strength is greater than
 ,
,
 is dominantly determined by two-photon coherence
is dominantly determined by two-photon coherence
 , since
, since
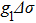 is far less than
is far less than
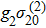 . In this case, the signal features can be explained by analysing the evolution of
. In this case, the signal features can be explained by analysing the evolution of
 . The real (imaginary) part of
. The real (imaginary) part of
 is shown in Figs. 5(a) 5((b)) and 5(c) 5((d)) for different coupling strengths and modulation indices, respectively. Where the parameters used in Figs. 5(a) (5(b)) and 5(c) (5(d)) are corresponding to Figs. 4(a) and 4(d), respectively. At
is shown in Figs. 5(a) 5((b)) and 5(c) 5((d)) for different coupling strengths and modulation indices, respectively. Where the parameters used in Figs. 5(a) (5(b)) and 5(c) (5(d)) are corresponding to Figs. 4(a) and 4(d), respectively. At
 , the imaginary part of
, the imaginary part of
 is zero, and the FWM process is governed mainly by the real part of
is zero, and the FWM process is governed mainly by the real part of
 , which gives rise to a largely suppression of FWM signals for an increasing dressing strength. As the modulation frequency is detuned away from the resonant position, the real part of this coherence decreases fast to zero, and then changes to a gain region with a damped oscillation behaviour, both the real part and imaginary part contribute to the splitting of peaks and the oscillation fringes. A similar evolution process can also be observed in the change of modulation index A as shown in Figs. 5(c) and 5(d). Thus, the control of FWM process can be achieved by tuning the dynamic parameters of the probe field and strengths of the inner-dressing fields.
, which gives rise to a largely suppression of FWM signals for an increasing dressing strength. As the modulation frequency is detuned away from the resonant position, the real part of this coherence decreases fast to zero, and then changes to a gain region with a damped oscillation behaviour, both the real part and imaginary part contribute to the splitting of peaks and the oscillation fringes. A similar evolution process can also be observed in the change of modulation index A as shown in Figs. 5(c) and 5(d). Thus, the control of FWM process can be achieved by tuning the dynamic parameters of the probe field and strengths of the inner-dressing fields.
Here we should point out that this dynamic and inner-dressing controlling method suffers the competition between EIT and CPT induced by probe and coupling fields, and by the modulation of the probe field as well, respectively. It is different from the process in the out-dressing system investigated in Refs. [25]–[28] where the control process is achieved mainly by the modulation of electromagnetically induced gratings (EIG) formed by the dressing fields via switching between bright and dark states.