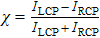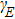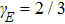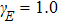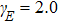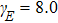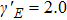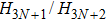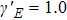† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61575077), the Natural Science Foundation of Jilin Province of China (Grant No. 20180101225JC), the China Postdoctoral Science Foundation (Grants Nos. 2018M641766 and 2019T120232), and the Graduate Innovation Fund of Jilin University, China (Grant No. 101832018C105).
We theoretically investigate the high-order harmonic generation (HHG) of helium atom driven by bichromatic counter-rotating circularly polarized laser fields. By changing the intensity ratio of the two driving laser fields, the spectral chirality of the HHG can be controlled. As the intensity ratio increases, the spectral chirality will change from positive- to negative-value around a large intensity ratio of the two driving fields when the total laser intensity keeps unchanged. However, the sign of the spectral chirality can be changed from positive to negative around a small intensity ratio of the two driving fields when the total laser intensity changes. At this time, we can effectively control the helicity of the harmonic spectrum and the polarization of the resulting attosecond pulses by adjusting the intensity ratio of the two driving laser fields. As the intensity ratio and the total intensity of the driving laser fields increase, the relative intensity of either the left-circularly or right-circularly polarized harmonic can be enhanced. The attosecond pulses can evolve from being elliptical to near linear correspondingly.
High-order harmonic generation (HHG) is a highly nonlinear phenomenon which serves as table-top sources of coherent, bright, extreme ultravilet (XUV) and soft-x-ray radiations.[1] The high harmonic can be used to generate isolated attosecond pulses and attosecond pulse trains for probing electron motion on attosecond time scale.[2] Many studies have been made to generate the supercontinuum spectrum by using linearly polarized laser fields which results in typically linearly polarized attosecond pulses. For example, a static electric field scheme,[3] the inhomogeneous laser field,[4] the chirped laser pulse,[5,6] and the two-color field[7–9] have been used to control the recolliding electron trajectory and smooth the harmonic spectrum. The HHG and isolated attosecond pulse generation in a synthesized two-color laser pulse with a wavelength-adjustable weaker pulse have also been investigated, an almost linearly polarized isolated attosecond pulse has been generated.[10] The similar coherent control of the light beams in the sum-frequency polarization beat is subtle. The polarization beat can be extended to any sum frequency of energy levels and becomes an ultra-fast process of effectively modulating attosecond pulses, which has been investigated both theoretically and experimentally.[11–13]
Circularly polarized harmonics are generated when the circularly polarized bichromatic fields interact with gas, which opens up the possibility and motivation of generating bright circularly polarized HHG.[14,15] A series of experiments investigating the ionization processes by changing the relative strength of the electric fields between the two colors in the two-color circularly polarized laser fields have been demonstrated.[16,17] Moreover, the bright circularly polarized harmonics have been generated by counterrotating circularly polarized laser fields.[14] Thus, this technique is realizable in the experiment to shape the polarization properties of the emitted attosecond pulses. The circularly polarized (CP) HHG of the ellipticity from linear to almost circular can be generated driven by bichromatic counter-rotating circularly polarized (BCCP) laser fields. Recently, the circularly-polarized light and the non-linearly polarized attosecond pulse have been a hot topic due to their applications of probing chiral-specific phenomena, such as ultrafast spin dynamics[14] and magnetic circular dichroism.[15]
The BCCP laser field consists of a circularly polarized fundamental field and its counter-rotating second harmonic, which results that the total field has the three-fold symmetry.[18] According to the angular momentum selection rules, only the harmonics orders 3N+1 and 3N+2 are allowed, while the 3N harmonics are forbidden in a BCCP laser field. Most recently, the control of the helicity of circularly polarized high harmonics has been achieved by changing the intensities of the two fields, and the elliptically polarized attosecond pulse trains (APTs) have been generated.[19,20] In the same respect, the time delay between the bichromatic laser fields can be adjusted to control either the right- or left-circularly polarized harmonics.[21] The generation of circularly polarized high-order harmonics has been investigated by controlling the electron recollisions, a classical trajectory analysis and quantum studies have been presented.[22] A scheme to generate tunable chirality of APTs from nearly linear to nearly circular has been illustrated by using the BCCP laser field, the results show that the ellipticity of the APTs is sensitive to the relative phase of the BCCP laser field.[23]
In this paper, we investigate the high harmonics generated in the two-dimensional (2D) helium atom model by the BCCP laser fields. The chirality of high harmonics and ellipticity of the APTs are illustrated by changing the intensity ratio of the two driving laser fields with different total intensities, and the ellipticity of the APTs can be varied correspondingly.
We investigate the HHG and attosecond pulse from helium atom interacting with a BCCP laser field based on the single-electron approximation. The harmonic spectrum generation can be investigated by numerically solving the two-dimensional time dependent Schrödinger equation (
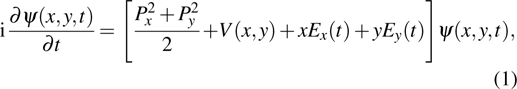 |
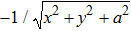
The dipole acceleration can be given according to the Ehrenfest theorem[27,28]
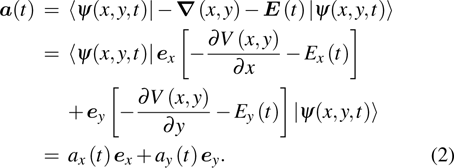 |
 |
 |
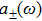
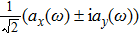
The temporal profile of an attosecond pulse can be obtained by superposing several harmonics
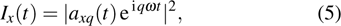 |
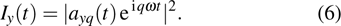 |
We investigate the helicity of harmonic generation from helium atom in a BCCP laser field. The BCCP laser field in the (x, y) polarization plane is given as[29,30]
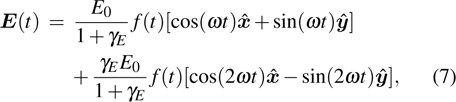 |
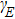
The spectral chirality can be characterized by the degree of chiral 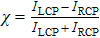
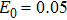
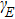

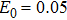
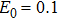
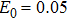
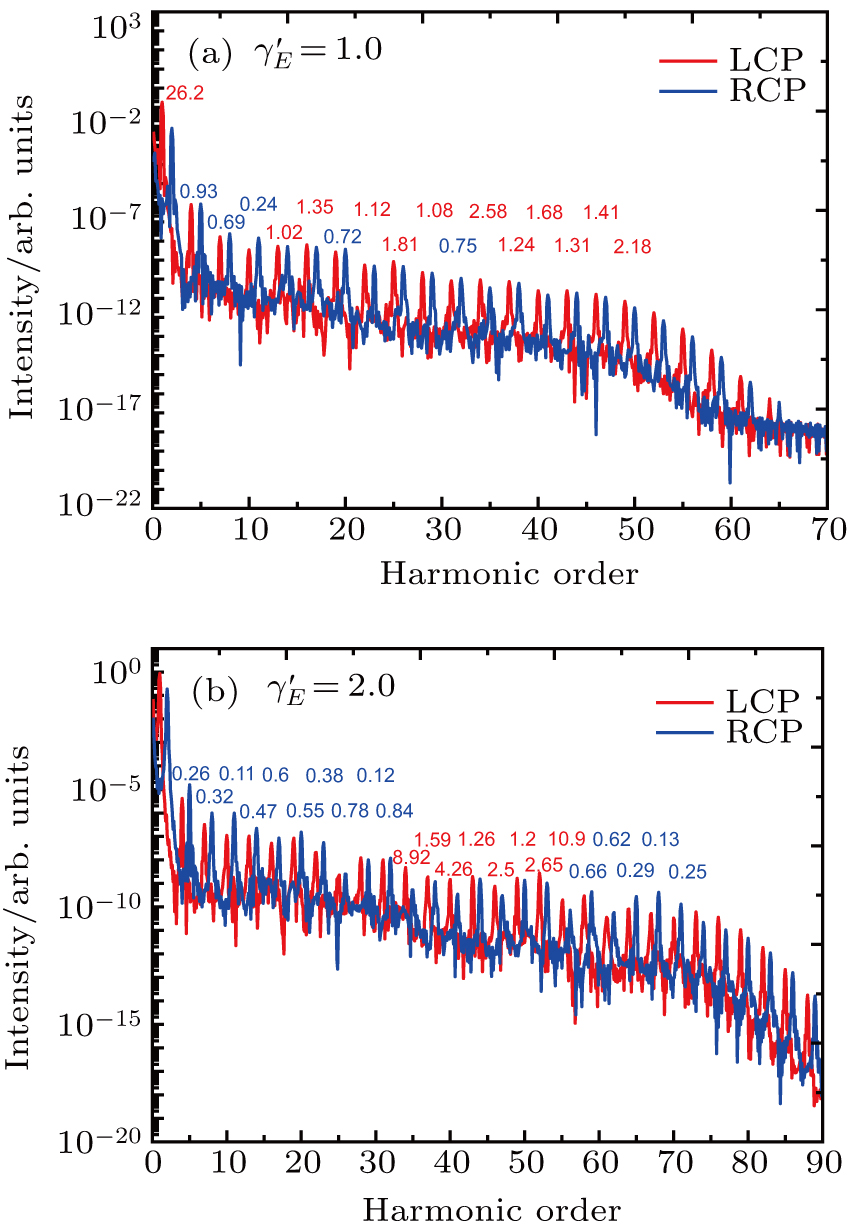
To further understand the underlying physical mechanisms, we will give a qualitative explanation. The HHG spectrum driven by a bichromatic circularly polarized laser field shows that only the harmonic orders 3N+1 (left circularly polarized harmonic) and 3N+2 (right circularly polarized harmonic) are allowed, while the 3N harmonic orders are forbidden. The 3N+1 order is generated by absorbing 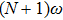
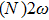
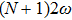

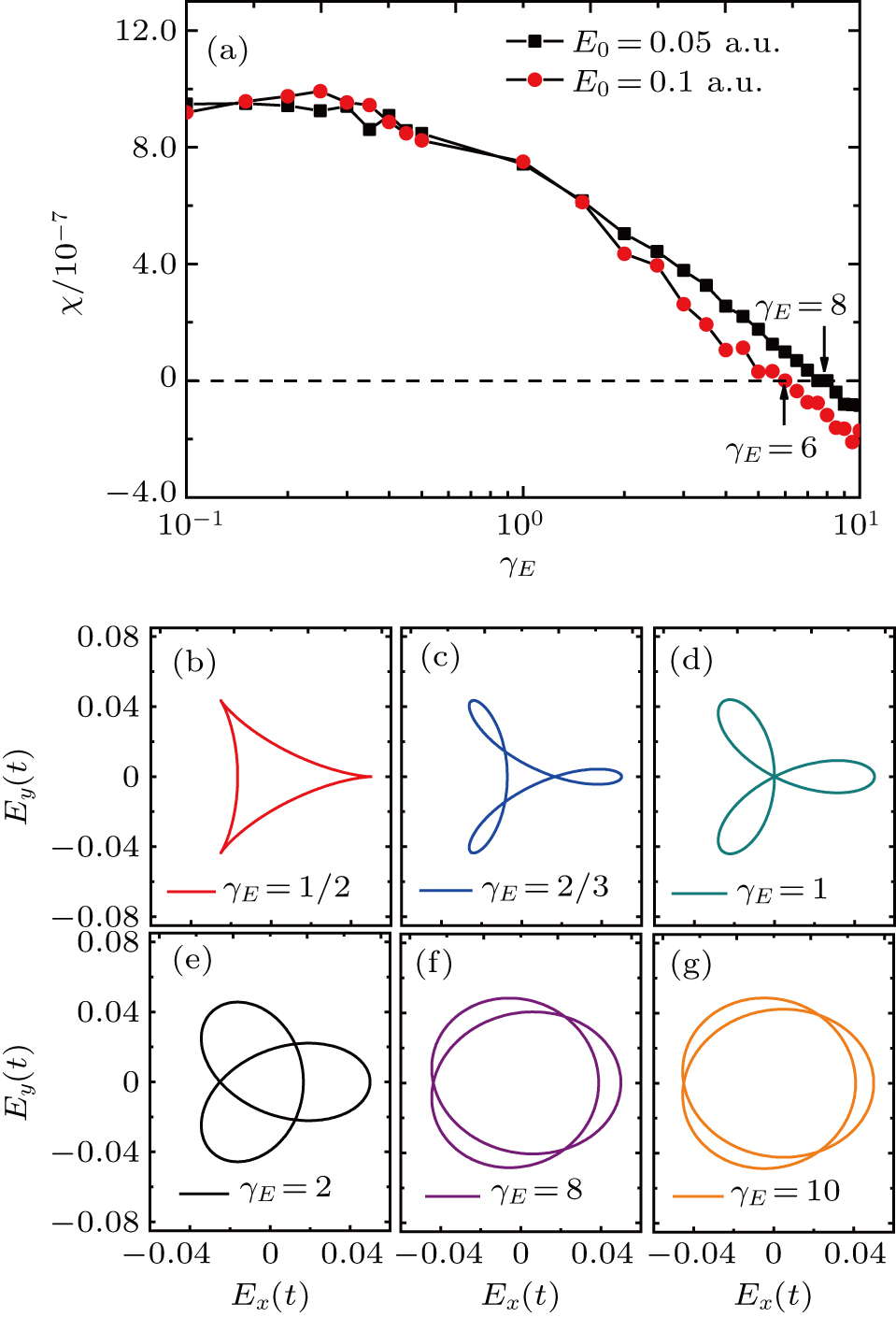
The Lissajous figures of the BCCP laser fields with different intensity ratios (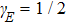
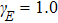
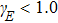
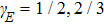
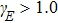
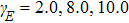

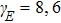
In order to control the spectral chirality effectively, we reconsider the laser field in the (x, y) polarization plane as
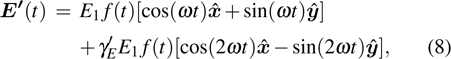 |
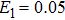
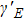
Figure 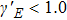


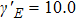
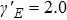
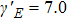
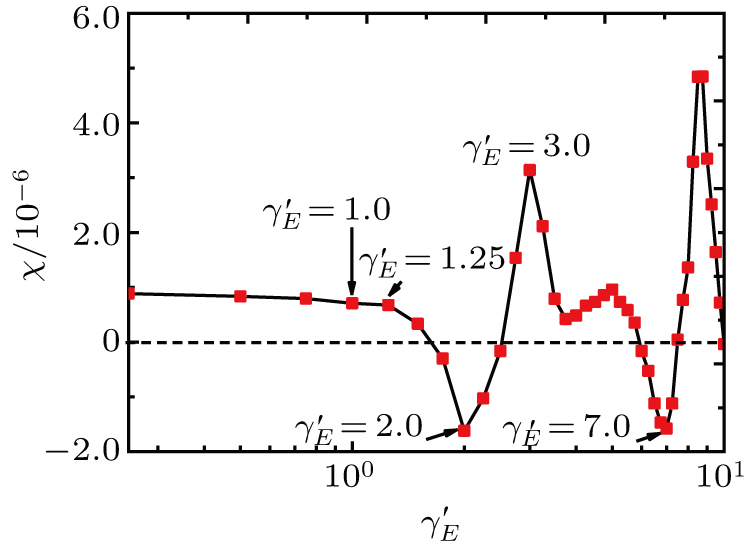 | Fig. 2. Spectral chirality as a function of the intensity ratio 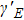

|
The physical explanation to that the spectral chirality of the HHG changes with the parameters of the bichromatic laser fields for the same total intensity as shown in Fig. 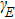
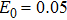
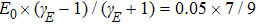
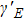
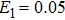
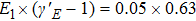
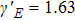

Due to the sign of the spectral chirality is more sensitive to the intensity ratios by the change of the total intensity compared with the case by the same total intensity, we will take 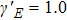
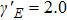
Figure 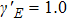
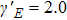
Figure 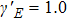
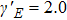
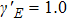
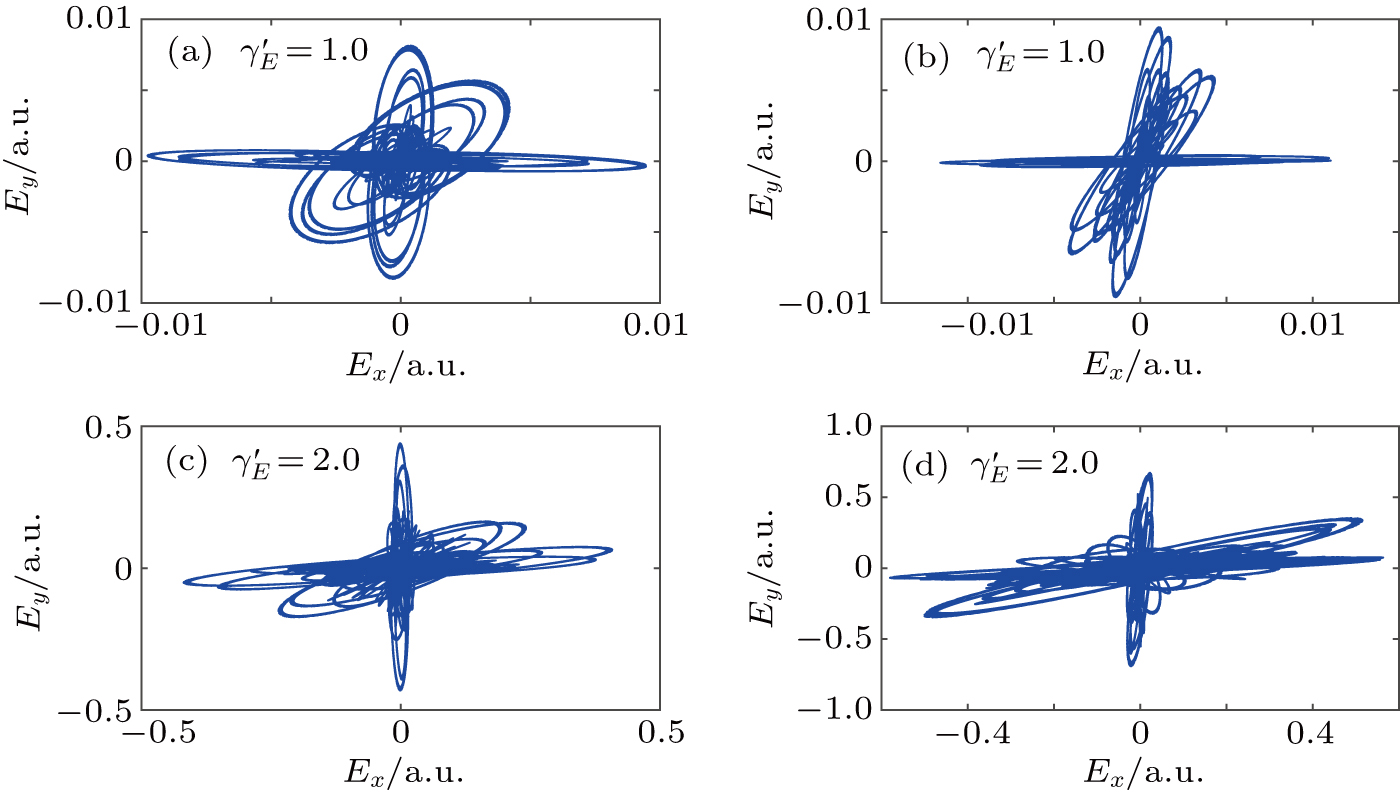
Next, we illustrate the attosecond pulse trains with different ellipticities obtained from our scheme with different intensity ratios as indicated in Fig. 
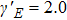
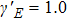
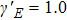
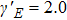
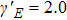
We have theoretically investigated the helicity of harmonic generation and the attsecond pulse polarization by solving the two-dimensional time dependent Schrödinger equation. The results show that the spectral chirality of high harmonics decreases slowly with the increase of the intensity ratio between the two driving fields at the same total intensity. The spectral chirality of high harmonics will change from positive- to negative-value with a large intensity ratio. We also investigate the control of the spectral chirality by adjusting the intensity ratio accompanied by the change of the total intensity. The sign of the spectral chirality can be changed at a small intensity ratio. At this time, either the right circularly polarized harmonic or the left circularly polarized harmonic is selectively enhanced. The elliptical and near linear attosecond pulse trains have been synthesized by superposing the proper harmonics.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] |