† Corresponding author. E-mail:
High-order harmonic generation below ionization threshold of He atom in the laser field is investigated by solving the three-dimensional time-dependent Schrödinger equation. An angular momentum-dependent model potential of He atom was used for getting the accurate energy levels of singlet states. The satellite-peak structures of the below-threshold harmonic generation (BTHG) of He are observed. We analyze the emission properties of the BTHG by employing a synchrosqueezing transform technique. We find that the satellite-peak structures have two types related to two kinds of transitions. One is the transition of the dressed states of the excited states, the other is the transition between the excited states and the ground state in the field-free case. Furthermore, our results show that the maximum Stark shift of the 2p state is about 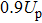

High-order harmonic generation (HHG) radiated from atoms or molecule in intense laser field has attracted considerable attention during the past decades. Based on their potential applications, such as attosecond time-resolved spectroscopy,[1,2] observation and control of the electronic dynamical processes in attosecond timescale,[3–6] researchers pay a close attention to the HHG at the plateau and near the cutoff region because its important application in ultra-short attosecond pulse. The generated high-energy photons can be well explained by the semiclassical three-step model.[7] First, the electron in atoms is ionized by the tunneling, then it propagates in the laser field and is driven back towards the parent ions (rescattering) and gains energy. Finally, the electron recombines into the ground state and emits the photons to produce the high-order harmonics. The maximum harmonic photon energy is located approximately at the cutoff energy 


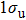

In this paper, we focus on the BTHG below the ionization threshold of He atom. We calculate the BTHG spectra of He atom by solving the three-dimensional time-dependent Schrödinger equation (TDSE) of He atom with the angular momentum model potential for the accurate bound states structures of the singlet state. We find not only the traditional odd peaks but also the satellite-peaks of the BTHG of He atom, and the origin of the satellite-peaks is explored by means of the time-frequency transform and the energy relation of the transitions.
The BTHG of helium atom in the laser field can be obtained by solving the TDSE of He atom with a single-electron approximation. In the length gauge, the TDSE of He atom in dipole approximation can be written as (atomic units are used, unless otherwise stated)
 |
 |
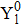
 |

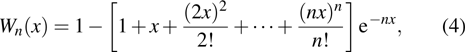 |

 |

The time-dependent generalized pseudo-spectral (short as TDGPS) method[21] is used to solve the TDSE (1) in spherical coordinates accurately. This method takes the non-uniform optimal spatial discretization of the coordinates. The time propagation of the wave function under this method is performed by the split operator method as follows:
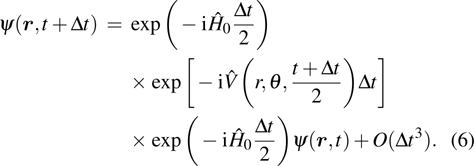 |
 |
The HHG power spectra in the length form can be obtained using the Fourier transformation of the time-dependent dipole moment 
 |
To understand the dynamic process of the HHG, we perform the time-frequency analysis by means of the synchrosqueezing transform (SST).[11] Compared with traditional TF techniques, such as Gabor transform, Morlet transform, etc., the SST can resolve the intrinsic blurring in the TF spectra below the ionization threshold and produce a clear spectrum.
By using the method mentioned above, we have calculated the BTHG of He atom in the laser field when the initial state of the atom is in the ground state. In our calculation, we choose a laser electric field with a 34-cycles and 
 | Fig. 1. The BTHG spectra of He atom driven by the laser pulses with different intensities (a) and wavelengths (b). |
In Fig. 
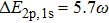
Next, we will recognize the contributions of excited states to the satellite-peaks of left-side of the 7th order near the end of the laser field. In Fig. 
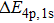

 |



 | Fig. 4. The BTHG spectra (a) of He in laser pulse with wavelength 470 nm, intensity 1.4×1014 W/cm2, and SST (b) analysis. |
 | Fig. 5. The BTHG spectra (a) of He in laser pulse with wavelength 425 nm, intensity 1.4×1014 W/cm2, and SST (b) analysis. |
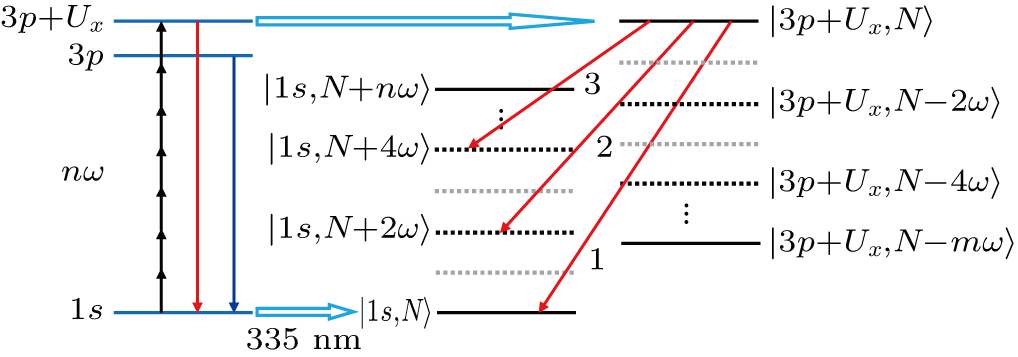
According to multi-photon process, the BTHG is the result of the transition between the dressed states formed by the same state in field-free (not shown in Fig. 
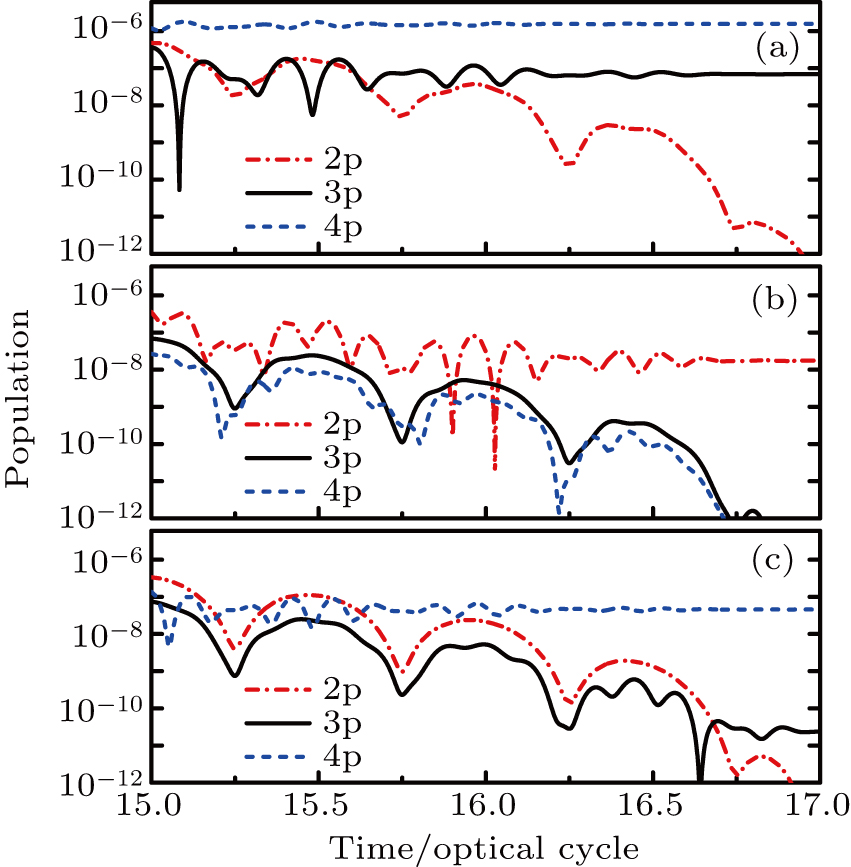
To study the characteristics of the satellite-peaks of the BTHG when only one excited state has a distinct population, for example, 2p state, we calculated the low-order harmonics of He atom driven by a laser pulse with the wavelength 470 nm and intensity I = 1.4×1014 W/cm2, and the corresponding time-frequency analysis (SST). Our results are shown in Fig. 

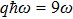


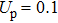


For the satellite-peaks of the 7th order, although the side peak does not appear in Fig. 

If we choose the laser wavelength is 425 nm, intensity is 1.4×1014 W/cm2, we calculated the BTHG of He atom. The results are shown in Fig. 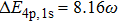
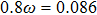


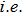
It should be pointed out that the position of the satellite-peaks of the BTHG would change with the laser intensity when the satellite-peak emission only comes from the transition between the dressed states in laser field. And when the satellite-peak emission originated from two kinds of transition, i.e., the transition between the dressed states in laser field and the excited state to ground state in field-free, for the part of the transition between the excited state to ground states in the field-free, the position of the satellite-peaks is independent of the laser intensity. If the contribution of the transition between the dressed states is dominant, the position of the satellite-peak will still change with the laser intensity (as shown in Fig.
For the analysis of the side peaks above is based on the energy relation of atomic energy levels and Stark shift, which include the transition of 4p–1s or 3p-1s (Fig.
In the first case (Fig.
We have investigated the BTHG emission of He atom driven by a laser pulse by solving 3D TDSE. In our study, we use the precise model potential of He atom, which can give the accurate singlet state energy levels. Meanwhile, we use the SST method to analyze the emission process of the BTHG in detail because the method has a high resolution for energy. In our study, we found the satellite-peaks of the BTHG for He atom appear. Through the analysis of SST, we are able to identify the contribution of some satellite-peaks only comes from the dressed states in laser field, and some peaks caused by the transition of the excited state to the ground state in field-free and of the dressed states in the laser field. For the former, we can explain the reason that the interval between the adjacent satellite-peaks is 2ω because the transition takes place in the dressed states formed from the different states in field-free. For the later, if only one excited state has high population, then the energy difference between the satellite-peaks and the main peak means the largest Stark shift for the excited state in laser field. Based on the structure of the satellite-peaks, we can obtain that the maximum Stark shift of 2p state for helium atom in the laser field is 

| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] |