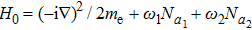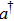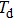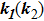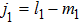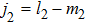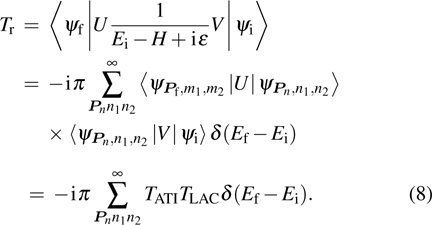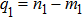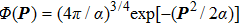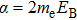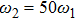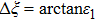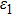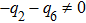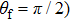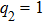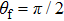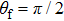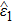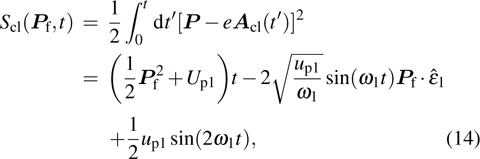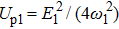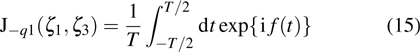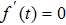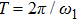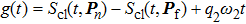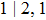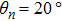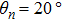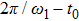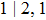Cite this Article
Zhou Xu-Cong, Shi Shang, Li Fei, Yang Yu-Jun, Chen Jing, Meng Qing-Tian, Wang Bing-Bing. Asymmetric structure of atomic above-threshold ionization spectrum in two-color elliptically polarized laser fields. Chinese Physics B, 2019, 28(10): 103201  
Permissions
Asymmetric structure of atomic above-threshold ionization spectrum in two-color elliptically polarized laser fields
Zhou Xu-Cong1, 2, Shi Shang2, 6, Li Fei2, 6, Yang Yu-Jun3, Chen Jing4, 5, Meng Qing-Tian1, Wang Bing-Bing2, 6, †
School of Physics and Electronics, Shandong Normal University, Jinan 250358, China
Laboratory of Optical Physics, Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China
Insititute of Atomic and Molecular Physics, Jilin University, Changchun 130012, China
HEDPS, Center for Applied Physics and Technology, Peking University, Beijing 100871, China
Institute of Applied Physics and Computational Mathematics, Beijing 100088, China
University of Chinese Academy of Sciences, Beijing 100049, China

 

† Corresponding author. E-mail: wbb@aphy.iphy.ac.cn

Abstract

According to the frequency-domain theory, we investigate the asymmetric structure of above-threshold ionization (ATI) spectrum of an atom in two-color elliptically polarized (EP) laser fields. When both laser fields are linearly polarized (LP), the spectrum shows that the multi-plateau structure is symmetric about the emitted angle of electron at π/2, while the spectrum becomes asymmetric and shifts rightwards with the increase of the EP degree of the IR laser field. Since the total ATI process is regarded as including direct ATI and the rescattering ATI, we analyze the spectrum structure of direct ATI and rescattering ATI separately. Using the saddle-point approximation, we find that for direct ATI, the fringes on the spectrum are mainly attributed to the fact that the ionization probability becomes very small when the direction of emitted electrons is perpendicular to the direction of the XUV laser polarization; while for the rescattering ATI, the interference fringes on the spectrum mainly come from the superposition of the waist structures on the spectra of all sub-channels.

PACS: 32.80.Rm;33.15.Dj;42.50.Hz;87.15.-v
Keyword:above-threshold ionization;elliptically polarized;two color laser fields;asymmetric structure
1. Introduction

In the last decades, the rapid development of ultrashort laser pulse technology has promoted the study of light-matter interactions. Especially when an atom or molecule is exposed to an intense laser field, a lot of novel phenomena, such as above-threshold ionization (ATI),[1,2] high-order above-threshold ionization (HATI),[3,5] high harmonic generation (HHG),[6,7] and non-sequential double ionization (NSDI),[8,9] may occur. These processes can be described by three-step model.[10] In this model, the bound electron in an atom or molecule can firstly absorb photons and be ionized by the strong laser. In the next step, the ionized electron is accelerated to escape from the parent ion. Finally, when the direction of laser field is reversed, part of ionized electrons can go back to the parent ion and collide with it. Some electrons can combine with the parent ion and then emit high energy photons, which process is called HHG; some may have an elastic collision with the parent ion, which may lead to the HATI; while part of electrons have inelastic collisions and cause another electron to be ionized, which is called NSDI. By using elliptical polarized laser fields, it was found that the probability and the cutoff of HATI spectrum decrease with the degree of the laser ellipticity increasing, which demonstrates the correction to the three-step model.[11]

Recently, the ionization of an atom in two-color laser fields is becoming a hotspot. Kazansky et al.[12] studied the angle-resolved spectra of photoelectrons by infrared and extreme ultraviolet (IR+XUV) two-color laser pulses. Radcliffe et al.[13] found a plateau-shape envelope of the ATI spectrum with increasing the intensity of the IR laser field. What is more, Zhang et al.[14] observed a step-like structure of ATI spectrum in IR+XUV two-color laser fields. Most of these studies are based on linearly polarized (LP) laser fields, because EP laser field is difficult to deal with experimentally and theoretically. Therefore, the ionization by an elliptically polarized (EP) laser pulse has attracted the attention of many scientists.[15,18] Busuladžić et al.[15] investigated the symmetry properties of molecular HATI spectra by changing the molecular orientation in an EP laser field. Li et al.[16] investigated the strong-field ionization dynamics of atoms in circularly polarized laser fields by a three-dimensional (3D) electron ensemble method. Furthermore, Yu et al.[17] explored the ionization dynamics of high-energy photoelectrons in EP laser fields. In this paper, we investigate the asymmetric structure for ATI of an atom in two-color EP laser fields.

2. Theoretical method

Here the ionization of the atom in two-color laser fields is taken as a research object. The laser field includes an EP laser field and an LP laser field. This atom–laser system can be regarded as an isolated system, where the total energy is conserved. Based on the frequency-domain theory, the Hamiltonian of this system is

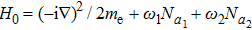
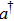
where represents the electron–photon energy operator, with and being the photon number operators of the two laser fields with different frequencies and , respectively, and with i = 1 and 2, where a and are the annihilation and creation operators of the photon mode respectively; U represents the atomic binding potential, and V is the electron–laser interaction potential and expressed as
where is the vector potential with , where with being the normalized volume of the laser field. The polarization state of the laser field is defined as , where the degree of the elliptical polarization is defined as , such that corresponds to circular polarization and corresponds to linear polarization.[19]

We now consider the ATI of an atom in a two-color laser field as a genuine scattering process. Using the formal scattering method,[20] the transition matrix element can be written as

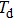
Here, the first term and the second term on the right-hand side of Eq. (3) correspond to the direct ATI and the rescattering ATI (i.e., HATI ), respectively. So equation (3) can also be written as , where is the process of the electrons being ionized by directly absorbing photons, while is the process of the electrons absorbing photons then going back to collide with the parent ion before it has been ionized.

The initial quantum state is expressed as , which corresponds to the eigenstate of the Hamiltonian with the associated energy , in which is the wavefunction describing the ground state of an atom, is the initial state of the laser field for (j = 1, 2), and Ip represents the threshold of the atom. The final state of the system can be denoted as , which is the Volkov state of the electron in the two laser fields, which can be expressed as

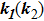
where is the normalized volume, is the final state momentum of ionized electron, , with being the ponderomotive potential in the first (second) laser field, and is the photon momentum of the first (second) laser field. The total energy of final state is
where m1 and m2 are photon numbers of the two laser fields, respectively.

The generalized Bessel function can be written as

with , where
On a whole, the direct ATI can be expressed as
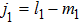
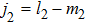
where , , with and j2 being the photon numbers of the electron absorbing from the two laser fields. And the transition matrix element of HATI is given by
In order to obtain Eq. (8), we utilize the completeness relation of the Volkov states . Therefore, the rescattering process can be divided into two parts, i.e., the ATI process and the laser-assisted LAC process.[21]
with , .

Finally, we can obtain[22]

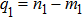
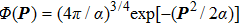
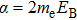
where , represent the number of the electrons absorbed from different fields in the LAC process. We assume that the initial phases of the two laser fields are both 0, which is for simplicity. The s wave function in the ground state of the momentum space is with . In this work, we employ the short potential to represent the interaction between the ionized electron and its parent ion. Atomic units are used throughout this work unless stated otherwise.

3. Numerical results

Firstly, we study the total angle-resolved ATI spectrum of hydrogen atom in two-color laser fields, which includes a beam of EP IR laser and a beam of LP XUV laser. The major axis of the EP laser field is along the z axis, and the minor axis is along the x axis. The LP laser field is along the z axis. The frequency of IR laser field is , and the field intensity is , while the frequency of the XUV laser is 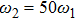and the field intensity is .

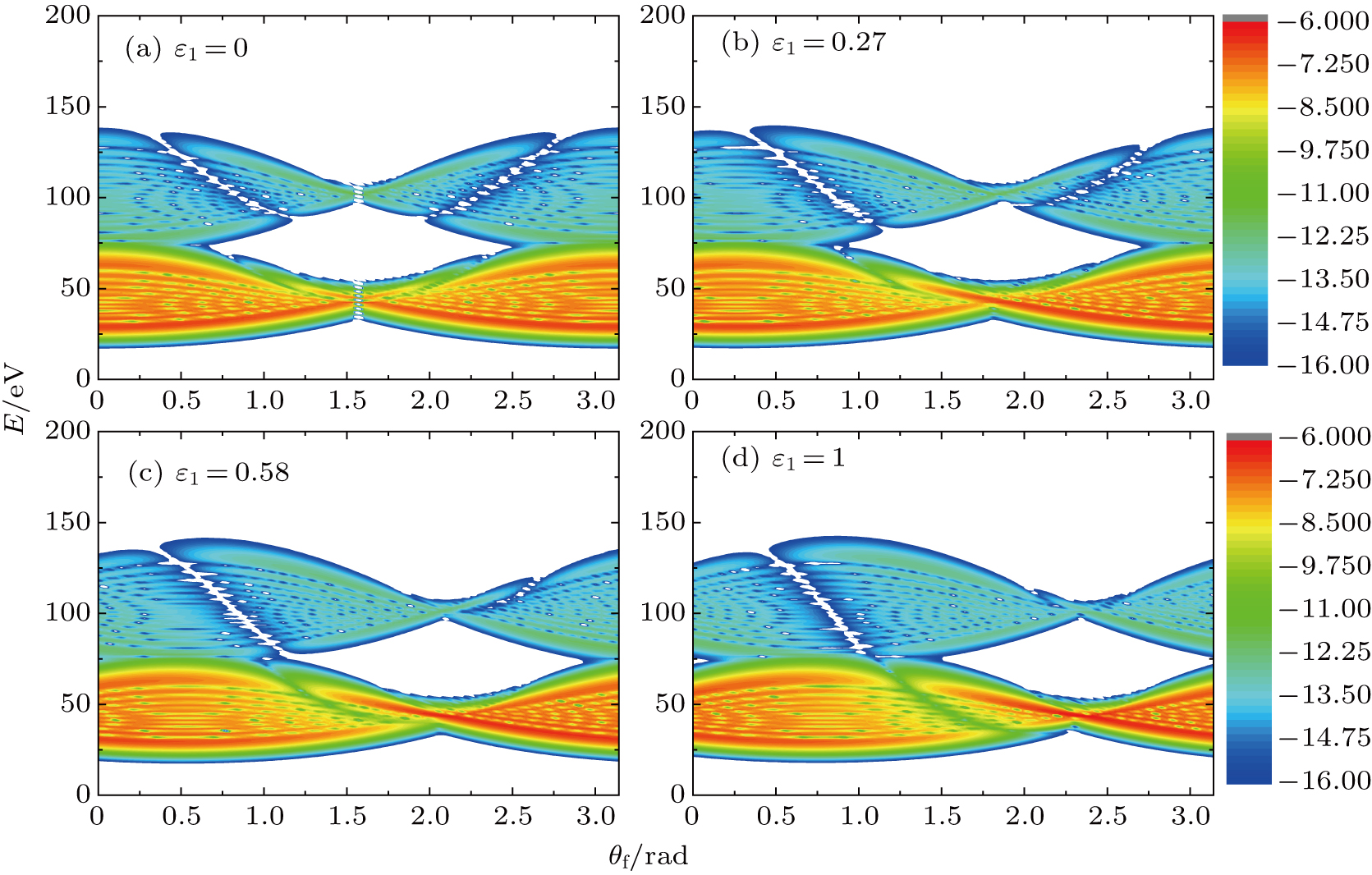
Figure 1 shows the total angle-resolved ATI spectrum of hydrogen atom for different values of right-handed EP degree of IR laser field, where is the angle between the momentum direction of the ionized electron and z axis. From Fig. 1, we can clearly see that the spectrum shows two plateaus, in which the probability of the first plateau is much larger than that of the second plateau. Especially, the total ATI spectrum is symmetric about the angle of in Fig. 1(a), when the IR laser is linearly polarized. However, the spectrum shows asymmetric for the IR laser becomes an EP field. Meanwhile, we can find that the spectrum shifts toward the right with the increase of the EP degree of the IR laser from Figs. 1(b)–1(d). This phenomenon can be easily understood as follows. For the EP IR laser, the ionization can be regarded as a tunneling ionization process, where the largest ionization probability is along the direction of the IR laser polarization, i.e., ; while for the XUV laser, the ionization can be regarded as a multiphoton ionization process, hence the ionization probability is not sensitive to the momentum direction of the ionized electron. As a result, the total angle-resolved ATI spectrum is mainly shifted by the EP laser field. Therefore, the greater the polarization degree of the EP laser field, the more the spectrum moves to the right.

Figure 1. Total angle-resolved ATI spectrum of H atom with (a), 0.27 (b), 0.58 (c), and 1 (d), and other parameters being , , , and .

By setting the spectral minimum point of the first plateau to be the reference point (marked by the arrows in Fig. 1), we may illustrate the shift of the spectrum versus the degree of the elliptical polarization of IR laser in Fig. 2, where the reference points are denoted by black square dots. Since the degree of the elliptical polarization is defined as , we can obtain the shift angle of the spectrum (denoted by red circle dots) from the formula 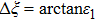. Figure 2 shows that the reference point curve coincide well with the curve of versus 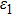. Moreover, the spectrum shift is strongly dependent on the polarization degree of EP laser field, and the spectrum shifts about π/4 as the polarization degree of the IR laser field changes from to 1. These results indicate that we may measure the degree of the laser elliptical polarization by angle-resolved ATI spectrum of atoms.

Figure 2. Spectrum shifting with polarization degree of EP laser field increasing.

Moreover, Figure 1 also shows the interference fringes on the two plateaus of the ATI spectrum. To explain these interference fringes on the spectrum, we analyze the total spectrum by two processes in the following: direct ATI and rescattering ATI.

Figure 3 depicts the direct ATI spectrum with different EP degrees of IR laser. The shift of the spectrum with EP degree is consistent with what we discussed above. We now focus on finding the cause of the interference fringes on the spectra. Under our present laser conditions, the generalized Bessel function in Eq. (7) can be reduced into

Figure 3. Angle-resolved direct ATI spectrum of H atom with (a), 0.27 (b), 0.58 (c), and 1 (d).

According to the property of the Bessel function, the Bessel function can be zero when for the order 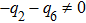, where corresponds to the case that the direction of emitted electrons is perpendicular to the XUV laser polarization (i.e., 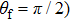. Therefore, the direct ATI spectra present the interference fringes for 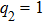and 2 at the angle 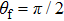. Moreover, since the Bessel function provides a small modulation in Eq. (11), the position of the interference fringes spreads a width around 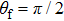. Figure 4 shows for the two plateaus of the direct ATI spectra by Eq. (12) with the sum for , −1, and 0. One may find that the spectra in Fig. 4 are consistent well with those of Fig. 3.

Figure 4. Values of by Eq. (12) as a function of with sum for , −1, and 0.

On the other hand, the width of each plateau on the direct ATI spectrum is found to be determined by the Bessel function under the present laser conditions. This Bessel function can be expressed as

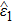
with . Here, the IR laser filed can be regarded as a classical field, where is the laser’s vector potential with E1 being the amplitude of IR laser field and the direction of the laser polarization. So the classical action of an electron in IR laser field is
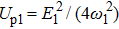
where is the ponderomotive energy of IR laser. Equation (13) becomes
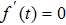
with . By using the saddle-point approximation, the saddle point t0 satisfies , which leads to the energy conservation relation as follows:
where q2 represents the number of XUV photons absorbed by the electron . Furthermore, we can obtain the final energy of ionized electron as follows:

By the saddle-point approximation, the beginning and the cutoff curves can be simulated by Eq. (16), and the results are shown in Fig. 5, indicating that they are also consistent well with the angle-resolved direct ATI spectrum.

Figure 5. Angle-resolved direct ATI spectrum of H atom with , beginning value (dashed line), and cutoff value (solid line of classical orbits at .

In the following part, we investigate the angle-resolved rescattering ATI spectrum with different EP degrees of IR laser and LP XUV laser as shown in Fig. 6.

Figure 6. Angle-resolved HATI spectrum of H atom with (a), 0.27 (b), 0.28 (c), and 1 (d), other parameters are , , , and .

Obviously, the angle-resolved HATI spectrum of H atom also shows clearly dip structures. In order to study the cause of the dip structures on the spectrum in detail, we divide the spectrum of HATI for into two parts depending on the different XUV photons absorbed by the electron as shown in Fig. 7.

Figure 7. Angle-resolved HATI spectrum for (a) the first plateau and (b) the second plateau.

Figure 7(a) shows the first plateau where the electron absorbs one XUV photon, while Figure 7(b) presents the second plateau where the electron absorbs two XUV photons. Obviously, the dip structure exists mainly on the second plateau.

According to the frequency-domain theory, we can regard HATI as two processes: ATI and LAC shown by Eqs. (9) and (10), respectively. In the following, we investigate the second plateau especially. We now define the channel (s2, , in which s2 and q2 refer to the electron-absorbed number of XUV photons in the ATI process and the LAC process, respectively. According to the above definition, the second plateau consists of three channels, (0,2), (1,1), and (2,0), where channels (1,1) and (2,0) are shown in Fig. 8. Channel (0,2) has little contribution to HATI, hence it may be ignored.

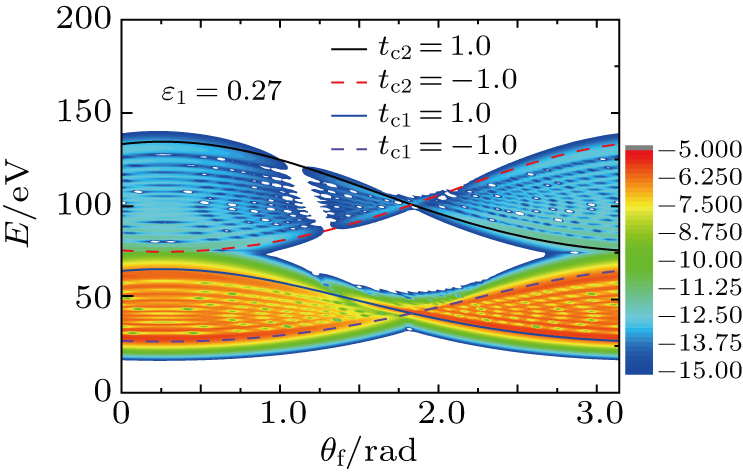
Figure 8. Angle-resolved HATI spectrum for (a) channel (1,1) and (b) channel (2,0).

From Fig. 8, we find that the dip structure of the second plateau mainly comes from the contribution of channel (1,1). In order to explain these dip structures, we investigate further channel (1,1) for different values of angle between the direction of electron momentum and the polarization direction of laser field, with , 40°, 60°, and 160° as shown in Figs. 9(a)–9(d). It is evident that all of the spectra show dip structures for four different angles, and the dip structure shifts rightwards with the increase of the angle.

Subsequently, we define sub-channel ( 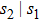, q2), where s1 is the number of IR photons absorbed by the electron in the ATI process. We show the spectra of different sub-channels in Fig. 9with sub-channel ( ) (Figs. 9(a1)–9(d1)), ( ) (Figs. 9(a2)–9(d2)), and ( ) (Figs. 9(a3)–9(d3)). By analyzing these sub-channels in detail, we find that the kinetic energy of the ionized electron increases with the increase of s1 value. It is easy to understand that the more the IR photons that are absorbed by the electron in the ATI process, the greater the kinetic energy that can be obtained by the electron. Besides, we can see that the location of dip structure in channel (1,1) corresponds to the waist structure of the sub-channels. Therefore, we find that the waist structure on the spectrum of channel (1,1) comes from the interference of all sub-channels, while the dip structure on it is attributed to the sum of the waist structures of all sub-channels.

Figure 9. Distribution of channel (1,1) with angle [(a), (a1)–(a3)], [(b), (b1)–(b3)], [(c) (c1)–(c3)], [(d), (d1)–(d3)] for [(a1)–(d1)] sub-channel (1 , 1), [(a2)–(d2)] ( ), and [(a3)–(d3)] ( ).

In order to further understand the interference fringes of the sub-channel in Fig. 9, we use the saddle-point approximation and analyze the Bessel function 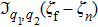in the LAC process in Eq. (10).[23] The Bessel function can be reduced into

For the Bessel function , it can be expressed in an integral form
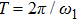
where . Like Eq. (15), now equation (19) becomes
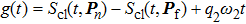
with . By using the saddle-point approximation, equation (20) can be rewritten as
where , and the saddle point t0 satisfies , and
Hence we obtain the energy conservation in the LAC process to be
where q2 represents the absorbed number of XUV photons in the LAC process. Finally, we derive the electron energy as follows:
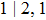
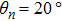
with being the kinetic energy of electron after the ATI process. So the energy of electron satisfies Eq. (23). In the following, we take the sub-channel ( ) for example, with , and the results are shown in Fig. 10.

Figure 10. Comparison between interference fringes of sub-channel ( ) and classical orbits with different values of collision moment and .

Additionally, we may find that the destructive interference appears in the angular distribution if , which indicates that the interference pattern is attributed to the interference of different orbits at collision moments t0 and 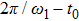in the LAC process.

The above analysis shows that the classical orbits are consistent well with the interference fringes, and these energy orbits come across the position of waist structure, where and the LAC process requires the electron momentum to be unchanged. However, electron absorbs one XUV photon in the LAC process in the sub-channel ( ). Therefore, it obviously violates the momentum conservation law and this is the reason why the destructive interference fringes occur at the waist structure. Meanwhile, equation (23) infers the waist structure shift rightwards with the increase of the laser ellipticity at the same .

4. Conclusions

In this work, we investigate the angle-resolved ATI spectra of H atom in different cases of EP two-color laser fields by using the frequency-domain theory. The spectrum presents asymmetric multi-plateau structure with interference fringes. It is found that the spectrum shifts with the increase of the EP degree of the IR laser filed. Furthermore, we study in detail the interference fringes on direct ATI spectrum and rescattering ATI spectrum. For the direct ATI, the fringes on the spectrum are mainly attributed to the fact that the ionization probability is very small when the direction of emitted electrons is perpendicular to the XUV laser polarization. While the interference fringes in the rescattering ATI spectrum mainly comes from the superposition of the waist structures of all sub-channels. This is because the electron momentum cannot keep conserved before and after the collision at some directions that the electron emits in the LAC process of the sub-channels. On the whole, the direct ATI process makes a dominate contribution to the whole ATI process.

Reference
[1] Agostini P Fabre F Mainfray G Petite G Rahman N K 1979 Phys. Rev. Lett. 42 1127
[2] Becker W Liu X Ho P J Eberly J H 2012 Rev. Mod. Phys. 84 1011
[3] Schafer K J Yang B DiMauro L F Kulander K C 1993 Phys. Rev. Lett. 70 1599
[4] Paulus G G Nicklich W Xu H Lambropoulos P Walther H 1994 Phys. Rev. Lett. 72 2851
[5] Walker B Sheehy B Kulander K C DiMauro L F 1996 Phys. Rev. Lett. 77 5031
[6] Li X F L’Huillier A Ferry M Lompre L A Mainfray G 1989 Phys. Rev. 39 5751
[7] L’Huillier A Balcou P 1993 Phys. Rev. Lett. 70 774
[8] Walker B Sheehy B DiMauro L F Agostini P Schafer K J Kulander K C 1994 Phys. Rev. Lett. 73 1227
[9] Becker A Faisal F H 1999 Phys. Rev. 59 R1742
[10] Corkum P B 1993 Phys. Rev. Lett. 71 1994
[11] Paulus G G Zacher F Walther H Lohr A Becker W Kleber M 1998 Phys. Rev. Lett. 80 484
[12] Kazansky A K Sazhina I P Kabachnik N M 2010 Phys. Rev. 82 033420
[13] Radcliffe P Arbeiter M Li W B Düsterer S Redlin H Hayden P Hough P Richardson V Costello J T Fennel T Meyer M 2012 New J. Phys. 14 043008
[14] Zhang K Chen J Hao X L Fu P Yan Z C Wang B 2013 Phys. Rev. 88 043435
[15] Busuladžić M Gazibegović-Busuladžić A Milošević D B 2009 Phys. Rev. 80 013420
[16] Li M Qin L Wu C Y Peng L Y Gong Q H Liu Y Q 2014 Phys. Rev. 89 013422
[17] Yu J Z Sun X F Shao Y Li M Gong Q H Liu Y Q 2015 Phys. Rev. 92 043411
[18] Wang Y L Yu S G Lai X Y Liu X J Chen J 2017 Phys. Rev. 95 063406
[19] Guo D S Drake G W F 1992 J. Phys. A: Math. Gen. 25 5377
[20] Gell-Mann M Goldberger M L 1953 Phys. Rev. 91 398
[21] Guo Y C Fu P Yan Z C Gong J Wang B 2009 Phys. Rev. 80 063408
[22] Zhang K Liu M Wang B Guo Y C Yan Z C Chen J Liu X J 2017 Chin. Phys. Lett. 34 113201
[23] Jin F Li F Yang Y Chen J Liu X Wang B 2018 J. Phys. B: At. Mol. Opt. Phys. 51 245601