Cite this Article
Lu Cun-Hao, Li Pu, Fang Yu-Ming. Efficient molecular model for squeeze-film damping in rarefied air. Chinese Physics B, 2019, 28(9): 098501  
Permissions
Efficient molecular model for squeeze-film damping in rarefied air
Lu Cun-Hao1, Li Pu1, †, Fang Yu-Ming2
School of Mechanical Engineering, Southeast University, Nanjing 211100, China
College of Electronic Science and Engineering, Nanjing University of Posts and Telecommunications, Nanjing 211100, China

 

† Corresponding author. E-mail: seulp@263.net

Abstract

Based on the energy transfer model (ETM) proposed by Bao et al. and the Monte Carlo (MC) model proposed by Hutcherson and Ye, this paper proposes an efficient molecular model (MC-S) for squeeze-film damping (SQFD) in rarefied air by releasing the assumption of constant molecular velocity in the gap. Compared with the experiment data, the MC-S model is more efficient than the MC model and more accurate than ETM. Besides, by using the MC-S model, the feasibility of the empirical model proposed by Sumali for SQFD of different plate sizes is discussed. It is proved that, for various plate sizes, the accuracy of the empirical model is relatively high. At last, the SQFD of various vibration frequencies is discussed, and it shows that, for low vibration frequency, the MC-S model is reduced to ETM.

PACS: 85.85.+j;47.45.Dt
Keyword:micro-electro-mechanical system (MEMS);squeeze-film air damping;rarefied air;molecular model
1. Introduction

Micro-electro-mechanical system (MEMS) devices, such as accelerometers, gyroscopes, and mirrors, have been widely used in many applications.[1–6] The air quality factor is one of the key characteristic parameters of MEMS devices.[7] When the microplate in MEMS devices is vibrating nearby the substrate, the air in the gap between the microplate and the substrate is squeezed in and out, which is called squeeze film.[8] Squeeze-film damping (SQFD) has been identified as an important mechanism of energy dissipation in microplates.[9] Over the past two decades, the SQFD effect on the dynamics of microplates has been extensively studied and many damping models have been proposed based on the continuum theory.[10–15] For higher performance of MEMS devices, one of the effective measures to reduce SQFD is to encapsulate the microplate in rarefied air.[16,17] In rarefied air, the inter-molecule collisions are so reduced that the gas under the microplate cannot be considered as a continuum, the viscous models based on the continuum theory may be questionable in this situation.[18–20] Therefore, for predicting SQFD in rarefied air, many molecular models have been proposed.[20]

Based on several assumptions for simplicity, Bao et al.[19] proposed a closed form energy transfer model (ETM) for SQFD in rarefied air. ETM is very simple to use and can directly show the relationship between the quality factor and the design parameters, including air pressure, gap distance, etc. However, noted by Hutcherson and Ye,[21] ETM suffers the large quantitative discrepancy due to the several assumptions, especially the assumption of constant molecular velocity in the gap. By releasing some assumptions of ETM, Hutcherson and Ye proposed a Monte Carlo (MC) numerical model, which shows higher accuracy than ETM. However, the huge computational cost makes the MC model hard to use. Considering the huge computational work of the MC model, Sumali[22] proposed a simple empirical model relating the ETM and MC model by fitting two data curves. However, pointed out by Sumali,[22] the empirical model has not been validated for SQFD of other plate sizes.

Based on the ETM and MC model, this paper gives an efficient molecular model (MC-S) by releasing the assumption of constant molecular velocity in the gap of ETM. The MC-S model can balance high accuracy and efficiency. Besides, by using the MC-S model, this paper discusses the feasibility of Sumali’s empirical model[22] for SQFD of different plate sizes. To our best knowledge, no paper has discussed the feasibility of the empirical model of different plate sizes. At last, the SQFD of various vibration frequencies is discussed. It should be noted that all plates discussed in this paper are rigid rectangular.

The outline of this paper is as follow. Section 2 gives brief introductions of ETM, the MC model, and the empirical model. In Section 3, the MC-S model is proposed. In Section 4, the results of the MC-S model are compared with the experiment data, the ability of the empirical model for different plate sizes is investigated by using the MC-S model, and the SQFD for various vibration frequencies is discussed. Section 5 gives a conclusion of the whole work.

2. Previous models
2.1. ETM

For SQFD of rectangular plates, Bao et al. have made several assumptions for simplicity:[19]

(i) Collisions of the gas molecule and plate are fully elastic and specula.

(ii) Molecular velocity in the gap between the plate and the substrate is assumed to be constant.

(iii) During the travel of a molecule in the gap, the velocity of the plate is assumed to be constant.

(iv) The gap length is assumed to be constant.

The number of molecules entering the gap per unit time is , where n is the concentration of molecules, the peripheral length of the plate, d the gap length, the average molecular velocity, k the Boltzmann constant, T the air temperature, and m the molecular mass. With the assumptions above, the number of collisions of a molecule traveling through the gap can be obtained. By calculating the change of kinetic energy of the gas molecules before and after passing through the gap, the total energy loss of the plate in one cycle is obtained as[19] where l2, , and have been approximated as the average traveling distance , , the molecule velocity and , meanwhile , p is the pressure, ρ is the gas density, and is the plate density. According to the definition of the quality factor, the analytical expression of ETM is written as[19] where Mm is the molar weight of the gas.

2.2. MC model and the empirical model

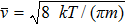
In the MC model, for higher accuracy, the assumptions (ii)–(iv) of ETM are released. The vibration period of the microplate is divided into M time divisions with an interval of . At the i-th time division, the number of molecules entering the gap is , . The kinetic energy change of a representative molecule entering at the i-th time division is calculated by tracking the motion of this molecule and recording the velocity changes after each collision with the plate. The initial position of the molecule is assigned on the basis of a uniform distribution, and the initial velocity is assigned as the average velocity . By summing up over M divisions, the quality factor of the MC model can be obtained as[21]

Although the MC model is much more accurate than ETM, the huge computational work makes it hard to use. By fitting the two data curves of ETM and MC model, Sumali proposed a very simple empirical formula relating the MC model and ETM[21] However, noted by Sumali,[22] the accuracy of the empirical model has not been verified for different plate sizes.

3. MC-S model

As can be seen, for releasing the assumptions of ETM, the MC model discretizes the vibration period of the plate, the initial velocity and the initial molecular position before entering the gap. However, these discretizations cost too much computational work. Based on ETM and the MC model, this paper proposes a new numerical model, which just releases assumption (ii). The process is shown as follows.[23]

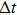
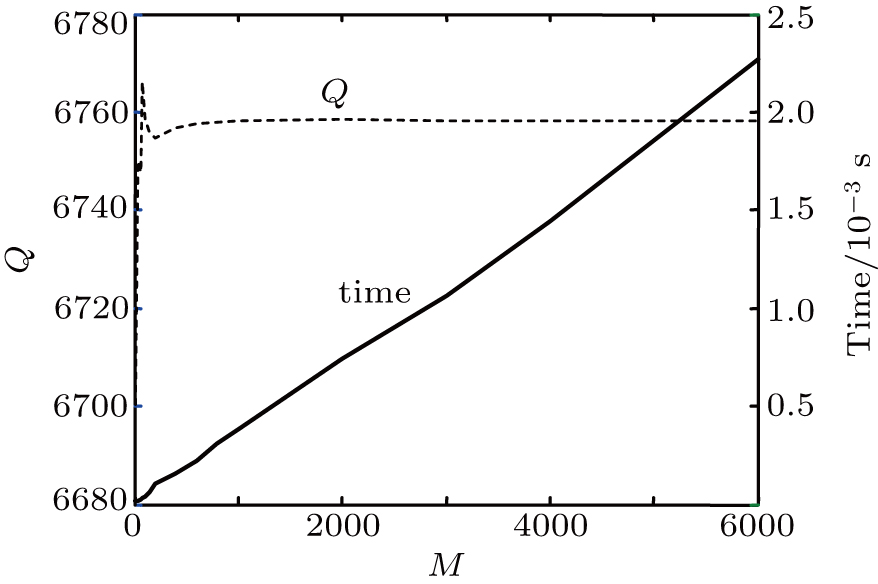
As with the MC model, the vibration period of the plate is divided into M time divisions with an interval of . When the molecule is going through the gap at the i-th time division, the velocity of the plate is considered to be constant . Due to the fully elastic and specula collisions of the molecule and the plate, the time of the molecule staying in the gap is calculated as , . At each collision with the plate, the molecule obtains a speed increment ,[19] For the first collision with the plate, the time cost is , . For the second collision, the time cost is . For the third collision, the time cost is , and so on. For the i-th time division, set the total collision times of a molecule and the plate as Ki, and the time cost is which should be less than or equal to the molecular travelling time in the gap , The calculation flow chart of Ki is shown in Fig. 1. By calculating all values of Ki of the M time divisions, the quality factor of the MC-S model can be obtained as[23]

Fig. 1. Calculation flow chart of Ki.
4. Comparisons
4.1. Vadiation of the MC-S model

To validate the MC-S model, Zook’s experiment data[17] is used. The parameters of Zook’s experiment are show in Table 1. Firstly, the convergence of M time divisions of the vibration period is discussed in Fig. 2. With less than 1000 time divisions, the results have converged to within 0.01%, and the computational time is less than 0.001 s, which shows high efficiency. Considering the computational work, the time division M is set as 1000, which can meet the convergence requirement.

Fig. 2. Convergence of simulation results at Kn = 561.
Table 1.

Parameters of Zook’s experiment.

.

Figure 3 gives the comparison of the quality factor. It is obvious that at Knudsen number (Kn) larger than 10, both the results of the MC model and MC-S model are more accurate than ETM. The curve of the MC-S model is very close to that of the MC model at the whole range of Kn. Table 2 lists the detailed values of the MC and MC-S models at .

Fig. 3. Comparison of quality factors in rarefied air.
Table 2.

Quality factors at .

.

In Table 2, the results of the MC-S model are slightly smaller than those of the MC model and are slightly closer to the experiment data. The largest deviation of MC-S model and MC model is less than 10%. Hutcherson and Ye[21] pointed that the main factor that influences the accuracy of ETM is assumption (ii), which may account for 90%. Assumptions (iii) and (iv) may take 10%. The MC-S model has just released assumption (ii) and the deviation is less than 10%, which also verifies that assumption (ii) is the main factor that influences the accuracy.

It may be confusing that the results of the MC-S model are slightly closer to the experiment data than those of the MC model. It should be noted that assumption (iii) considers the traveling time of each molecule entering the gap is smaller than the vibration period, which means during the vibration period, all molecules entering the gap can go through the gap. Actually, some gas molecules cannot go through the gap within a vibration period. As a result, assumption (iii) would slightly overestimate the energy change of molecules in the gap, and also underestimate the quality factor, which may explain that the MC-S model is “more accurate” than the MC model.

4.2. Empirical model of Sumali

Considering the huge computational work of the MC model, Sumali proposed a simple empirical formula to relate the ETM and MC model. The formula is fitted by two data curves. However, for SQFD of different plate sizes, the feasibility of the empirical model needs to be validated.[22]

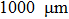
By using the MC-S model, this paper discusses the feasibility of the empirical model for various plate sizes. Zook’s experiment parameters are still used, plate length a and other parameters keep constant, while plate width b varies from to . Figure 4 gives the quality factors at , 100, 200, 500. The results of the empirical model agree well with those of the MC-S model at the whole range of b. However, the results of ETM are much larger than those of the other models. Table 3 gives the quality factor error at Kn = 500. The biggest error between the empirical model and MC-S model is 15%. As b increases, the quality factor error decreases. In general, it validates that the empirical model proposed by Sumali can have relatively high accuracy for various plate sizes.

Fig. 4. Quality factors of (a)–(d) Kn = 10, 100, 200, 500 at various plate widths.
Table 3.

Errors of quality factor at Kn = 500.

.
4.3. Limitation of the MC-S model

The MC-S model has calculated the SQFD of different Kn and different plate sizes, and the results are consistent with Sumali’s empirical model. Next, the MC-S model is used to study the SQFD of different vibration frequencies. Zook’s experiment parameters are still used, where the vibration frequency f varies from 500 Hz to 550000 Hz. Figure 5 shows the comparisons of quality factor at different frequencies. As can be seen, for different plate width b, the results of the MC-S model show a mutation with vibration frequency f. At small f, the results of the MC-S model agree with those of ETM; at large f, the results of the MC-S model become close to those of Sumali’s model. Besides, the frequency of quality factor mutation varies at different plate widths. At b = 40 m, the mutation of MC-S model occurs around 100000 Hz; at b = , it is around 40000 Hz; at , it is around 20000 Hz; at , it is around 10000 Hz. The frequency of mutation of the MC model decreases as the plate size increases. The reasons are shown as follows.

Fig. 5. Quality factors of Kn = 200 at different frequencies with (a) , (b) , (c) , (d) .

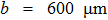
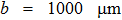
If assumption (ii) of constant molecular velocity is retained, the MC-S model is directly reduced to ETM The molecular velocity change due to the collision with the plate is reduced as the vibration frequency drops. When the vibration frequency drops to a certain extent, the values of Ki calculated by Eq. (5) are equal to those calculated by Eq. (7), and the MC-S model is reduced to ETM. So at small f, the curves of the MC-S model and ETM are the same in Fig. 5. When the frequency is relatively large, the molecular velocity change is large, which has an impact on Ki. The value of Ki calculated by Eq. (7) is larger than that of Eq. (5). So at large f, the results of the MC-S model start to be close to Sumali’s model in Fig. 5.

In order to simplify the SQFD model, the MC-S model does not discretize the initial position and direction of movement of gas molecules in the gap. Figure 6 shows the simulation diagrams of MC-S model and MC model. In Fig. 6(a), for the MC-S model, as with ETM, the position where gas molecules enter the gap is simplified to a fixed position, and the molecular velocity entering the gap is simplified to and . In Fig. 6(b), the MC model discretizes the initial position and direction of movement of gas molecules in the gap. Therefore, for a small plate size or a low vibration frequency, the results of the two simulation models in Fig. 6 are quite different. However, for a large plate size or a high vibration frequency, the difference between the two methods is small. In general, the MC-S model is also limited by the simplified model as with ETM. For relatively low frequency SQFD, the MC-S model is reduced to ETM.

Fig. 6. Simulation diagrams of (a) MC-S model and (b) MC model.
5. Conclusion

Based on the MC model and ETM, this paper proposes an MC-S model for SQFD in rarefied air. By releasing the key assumption of constant molecular velocity in the gap, the MC-S model has been proved to be more efficient than the MC model and more accurate than ETM. According to the above comparisons, the deviation between the MC-S model and MC model is less than 10%, and the simulation time of the MC-S model is less than 0.001 s. By using the MC-S model, the feasibility of the empirical model proposed by Sumali for SQFD of different plate sizes is discussed. The results verify that, for various plate sizes, the accuracy of the empirical model is still relatively high.

At last, this paper investigates the SQFD for various vibration frequencies. The results show that, for low vibration frequency, the MC-S model is reduced to ETM. The reason is that, for simplification, neither the MC-S model nor ETM discretizes the initial position and direction of movement of gas molecules in the gap. For large plate size or relatively high vibration frequency, the difference between the MC-S model and the MC model is small.

Reference
[1] Shi S L Chen D P Jing Y P Ou Y Ye T C Xu Q X 2010 Chin. Phys. B 19 076802 https://doi.org/10.1088/1674-1056/19/7/076802
[2] Wang D L Hao Y Q Zhai F X Yang K Liu H Q Chen Q Xie H K 2018 Chin. Phys. Lett. 35 120701 https://doi.org/10.1088/0256-307X/35/12/120701
[3] Zeng H J Li T Jin Q H Xu F F Wang Y L 2012 Chin. Phys. Lett. 29 126101 https://doi.org/10.1088/0256-307X/29/12/126101
[4] Zhang L M Jiao B B Yun S C Kong Y M Ku C W Chen D P 2017 Chin. Phys. Lett. 34 025101 https://doi.org/10.1088/0256-307X/34/2/025101
[5] Qiu H C Dara F Wu X Z Helmut S 2014 Chin. Phys. B 23 027701 https://doi.org/10.1088/1674-1056/23/2/027701
[6] Lei L H Li Y Fan G F Wu J J Jian L Cai X Y Li T B 2014 Chin. Phys. B 23 118703 https://doi.org/10.1088/1674-1056/23/11/118703
[7] Ishfaque A Kim B 2017 Nonlinear. Dyn. 87 1603 https://doi.org/10.1007/s11071-016-3136-z
[8] Bao M H Yang H 2007 Sens. Actuators A 136 3 https://doi.org/10.1016/j.sna.2007.01.008
[9] Li P Fang Y M Xu F F 2014 J. Sound Vib. 333 2688 https://doi.org/10.1016/j.jsv.2013.12.028
[10] Veijola T 2004 J. Micromech. Microeng. 14 1109 https://doi.org/10.1088/0960-1317/14/7/034
[11] Veijola T 2006 Microfluid Nanofluid 2 249 https://doi.org/10.1007/s10404-005-0072-5
[12] Li W L 2008 Microsyst Technol. 14 315 https://doi.org/10.1007/s00542-007-0479-x
[13] Pandey A K Pratap R 2008 Microfluid Nanofluid 4 205 https://doi.org/10.1007/s10404-007-0165-4
[14] Lee J W 2011 J. Mech. Sci. Technol. 25 3005 https://doi.org/10.1007/s12206-011-0820-2
[15] Fang Y M Li P Yang F Zuo W L 2016 Microfluid Nanofluid 20 152 https://doi.org/10.1007/s10404-016-1816-0
[16] Leung R Cheung H Gang H Ye W J 2010 Microfluid Nanofluid 9 809 https://doi.org/10.1007/s10404-010-0597-0
[17] Zook J D Burns D W 1992 Sens. Actuators A 35 51 https://doi.org/10.1016/0924-4247(92)87007-4
[18] Christian R G 1966 Vaccum 16 175 https://doi.org/10.1016/0042-207X(66)91162-6
[19] Bao M H Yang H Yin H Sun Y C 2002 J. Micromech Microeng. 12 341 https://doi.org/10.1088/0960-1317/12/3/322
[20] Lu C H Li P Bao M H Fang Y M 2018 J. Micromech. Microeng. 28 085003 https://doi.org/10.1088/1361-6439/aabdc0
[21] Hutcherson S Ye W J 2004 J. Micromech. Microeng. 14 1726 https://doi.org/10.1088/0960-1317/14/12/018
[22] Sumali H 2007 J. Micromech. Microeng. 17 2231 https://doi.org/10.1088/0960-1317/17/11/009
[23] Lu C H Li P 2018 5th International Conference on Mechanics and Mechatronics Research July 19–21, 2018 Tokyo, Japan 417 012006