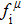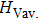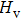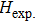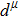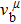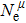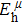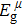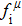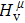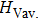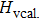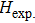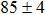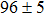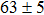† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 21671168 and 21875205), the Hebei Natural Science Foundation, China (Grant No. B2015203096), and the Qinhuangdao Science and Technology Support Program, China (Grant No. 201703A014).
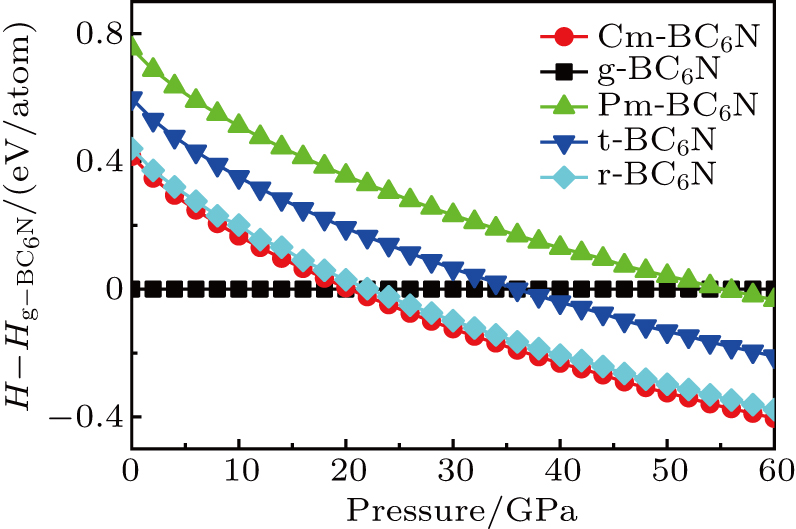
Via structural searching methodology and first-principles calculations, we predicted two new BC6N allotropes, a C-centered monoclinic BC6N (Cm-BC6N) and a primitive-centered monoclinic BC6N (Pm-BC6N). The lattice vibrations, elastic properties, ideal strength, theoretical hardness, and electronic structure of the predicted BC6N were investigated systematically. Our results reveal that Cm-BC6N is more favorable energetically than graphite-like g-BC6N above 20.6 GPa, which is lower than the transition pressures of r-BC6N, t-BC6N, and Pm-BC6N. Both Cm-BC6N and Pm-BC6N are indirect semiconductors with band gaps of 2.66 eV and 0.36 eV, respectively. Cm-BC6N exhibits the excellent ideal shear strength of 53.9 GPa in (011)[01 
Due to its broad industrial applications, superhard material is always of great scientific interest.[1,2] As we all know, the diamond and cubic boron nitride (c-BN) are well-studied superhard materials with excellent physical properties, such as wide band gaps, high hardness and thermal conductivity, large shear and bulk modules. However, the adhibition of diamond has been conditioned by its own imperfections, including brittleness, reacting with iron easily, and generating oxidizing reaction in the air at a high temperature. Cubic boron nitride shows better performance than diamond above, but its hardness and mechanical properties are obviously weaker than those of diamond.[3] B–C–N ternary system is considered to be harder and stronger than c-BN, chemically and thermally more stable than diamond.[4] Therefore, searching superhard materials from the B–C–N ternary system has been a focus of scientific research. Zhao et al.[5] successfully synthesized stoichiometric c-BC2N and c-BC4N crystals with diamond-like structures by using a diamond-anvil cell. Then Fan et al.[6–15] did systematic investigations of these structures based on the first-principles calculations, such as crystal structure, band gap, optical spectrum, ideal strength and hardness, in order to establish facts and reach new conclusions.
As we know that B–C–N compounds can consist of the typical sp3 covalent bonds containing B–C, B–N, C–N, and C–C bonds, the mechanical properties thus would be better with the increase of carbon content.[16–18] Graphite-like BC6N (g-BC6N)[19] has been found as an n-type semiconductor, which was synthesized by the chemical vapor deposition. The diamond-like t-BC6N and r-BC6N were proposed by Luo et al.,[20] which were obtained by replacing two carbon atoms in the eight-atom cubic diamond unit cell with a nitrogen atom and a boron atom. According to their results, the Vickers hardness of the two BC6N phases is about 80 GPa, higher than that of c-BN (66 GPa) and c-BC2N (76 GPa). In fact, the first-principles and their evolution methods are always used in predicting possible crystal structures or interpreting the mechanical properties of superhard materials.[21,22]
In the present work, a C-centered monoclinic BC6N (Cm-BC6N) and a primitive-centered monoclinic BC6N (Pm-BC6N) are proposed by structure searching method based on first-principles calculations. The structural, electronic, and mechanical properties of the proposed BC6N allotropes are investigated systematically. The Cm-BC6N and Pm-BC6N have dynamical and mechanical stability in ambient circumstance. We not only find their semiconductor nature from the band structures, but also can draw a conclusion that Cm-BC6N is more favorable than the previous predicted t-BC6N and r-BC6N in thermodynamics. By computing the ideal strength and theoretical hardness, we find out the superhard nature structures.
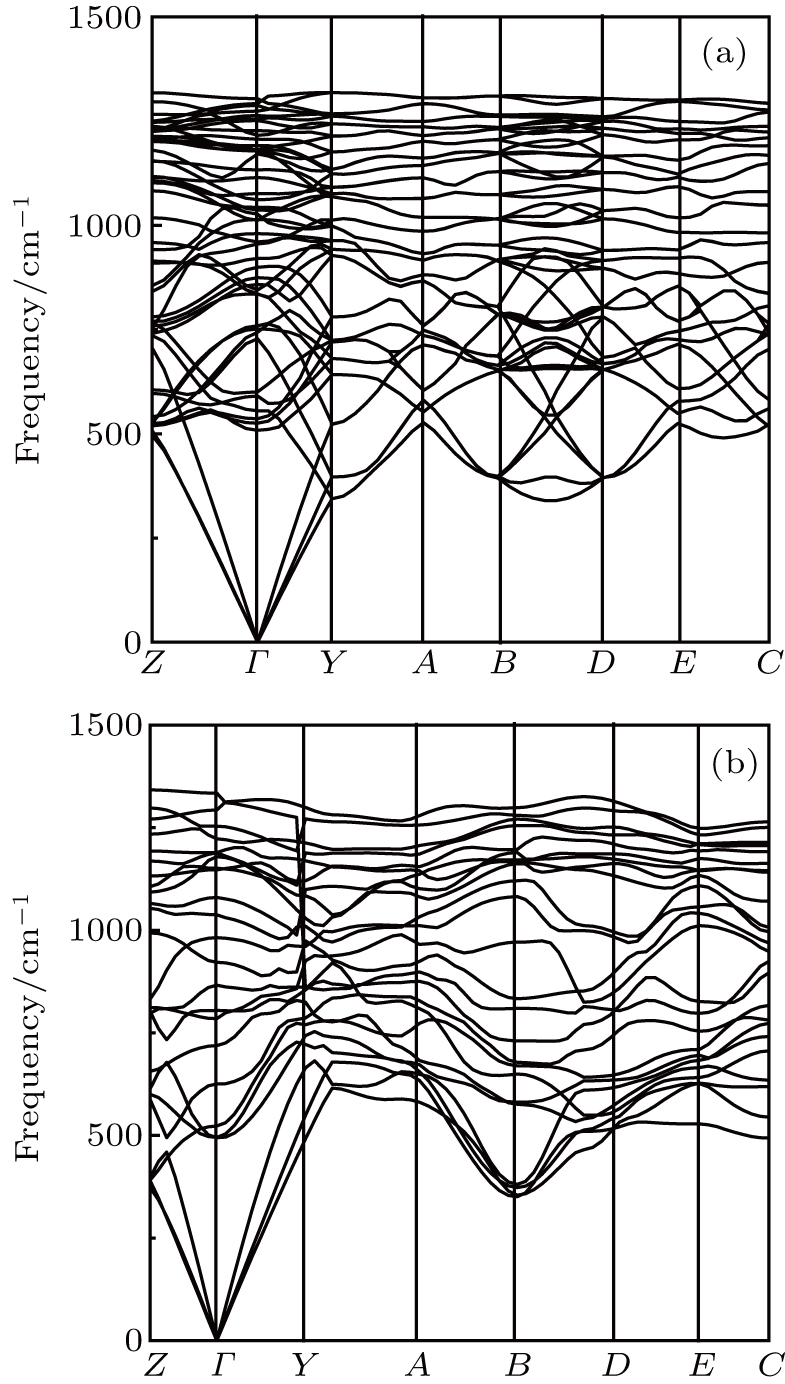
Crystal structures of Cm-BC6N and Pm-BC6N were explored by using the evolutionary methodology through particle swarm optimization as implemented in CALYPSO package,[23,24] which has successfully predicted various structures.[25–28] Subsequent structural relaxation and property calculations were performed based on the density functional theory[29,30] with the Vienna ab initio simulation software package (VASP) code, with a projector augmented wave (PAW) scheme[31] to show the electrons–ion interaction. The generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE)[32] functional was employed to describe the exchange and correlation potentials. From our text data, a plane-wave kinetic energy cutoff of 500 eV and quantitative value of k-points sampling of 0.25 Å−1 in Brillouin zone were used to give good convergence of the total energies. Optimization of the internal atomic positions and the lattice parameters was achieved by the minimization of forces and stress tensors. After calculating the elastic constants, the bulk modulus and shear modulus were figured out following the Voigt–Reuss–Hill (VRH) approximations.[33] From the local density approximation in plane wave basis, the phonon dispersions were calculated by the density functional perturbation theory, which has been implemented the Quantum ESPRESSO code[34] with the Troullier–Martins (TM) pseudopotentials.[35] Static enthalpy differences calculated relative to the graphite-like g-BC6N structure for the various structures are plotted in Fig.
The optimized structures of Cm-BC6N and Pm-BC6N are shown in Figs.
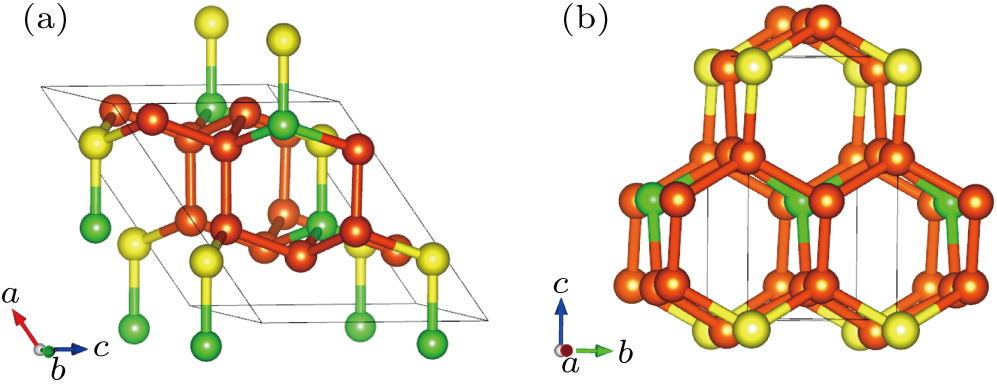 | Fig. 1. Structures of (a) Cm-BC6N and (b) Pm-BC6N; the yellow, orange, and green spheres represent B, C, and N atoms, respectively. |
| Table 1.
The equilibrium lattice parameters of a, b, c, density ρ, volume, and atomic positions. . |
To assess the thermodynamic stability of the BC6N (Cm-BC6N, Pm-BC6N, t-BC6N, and r-BC6N) phases, the relative enthalpies (without temperature effect) are calculated at the pressure range of 0–60 GPa. The pressure–enthalpy relationship calculated for all BC6N phases is shown in Fig.
By the Hookeʼs law, we calculate the single-crystal zero-pressure elastic constants Cij to comprehend Cm-BC6N and Pm-BC6N in elastic stability and mechanical properties.[44] For monoclinic symmetry, there are thirteen independent single-crystal elastic constants. As shown in Table
| Table 2.
Calculated zero-pressure elastic constants Cij (GPa), bulk modulus B (GPa), shear modulus G (GPa), Youngʼs modulus E (GPa), and Poissonʼs ratio υ of Cm-BC6N and Pm-BC6N. . |
Superhard materials not only manifest high bulk and shear moduli but also exhibit low Poissonʼs ratio, because of hardness strongly depending on the plastic deformation.[41] Additionally, the Voigt–Reuss–Hill approximation is used to reckon the polycrystalline elastic moduli as the Cij have been calculated, and the results are listed in Table 
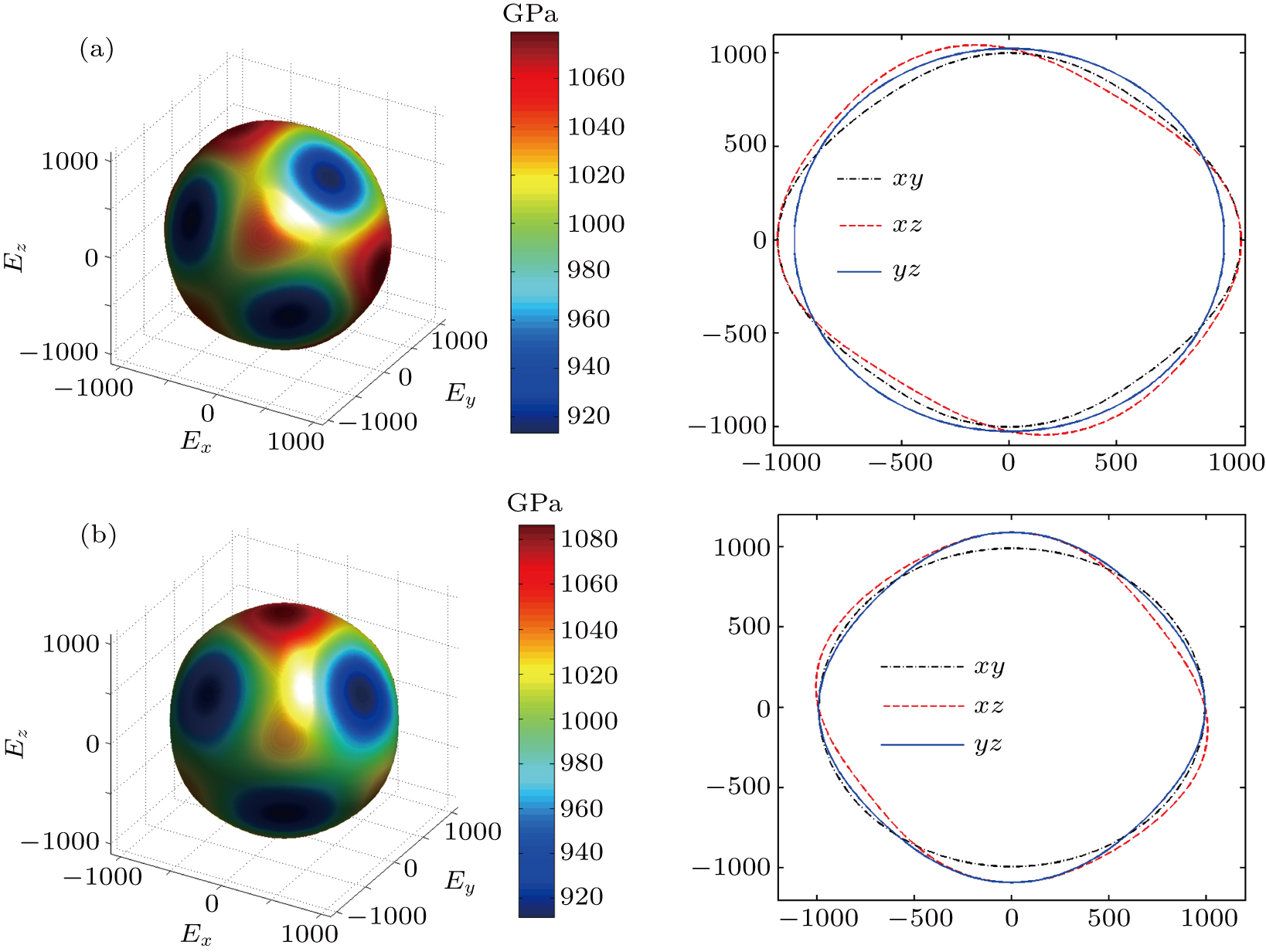
The Youngʼs module (E) is one of the most important parameters which measures the stiffness of a solid material. We show the three-dimensional (3D) representation and the corresponding two-dimensional (2D) projection of the Youngʼs modulus for Cm-BC6N and Pm-BC6N and in Fig. 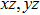
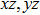
The calculated electronic band structure and density of states (DOS) of Cm-BC6N and Pm-BC6N at 0 GPa are presented in Fig. 
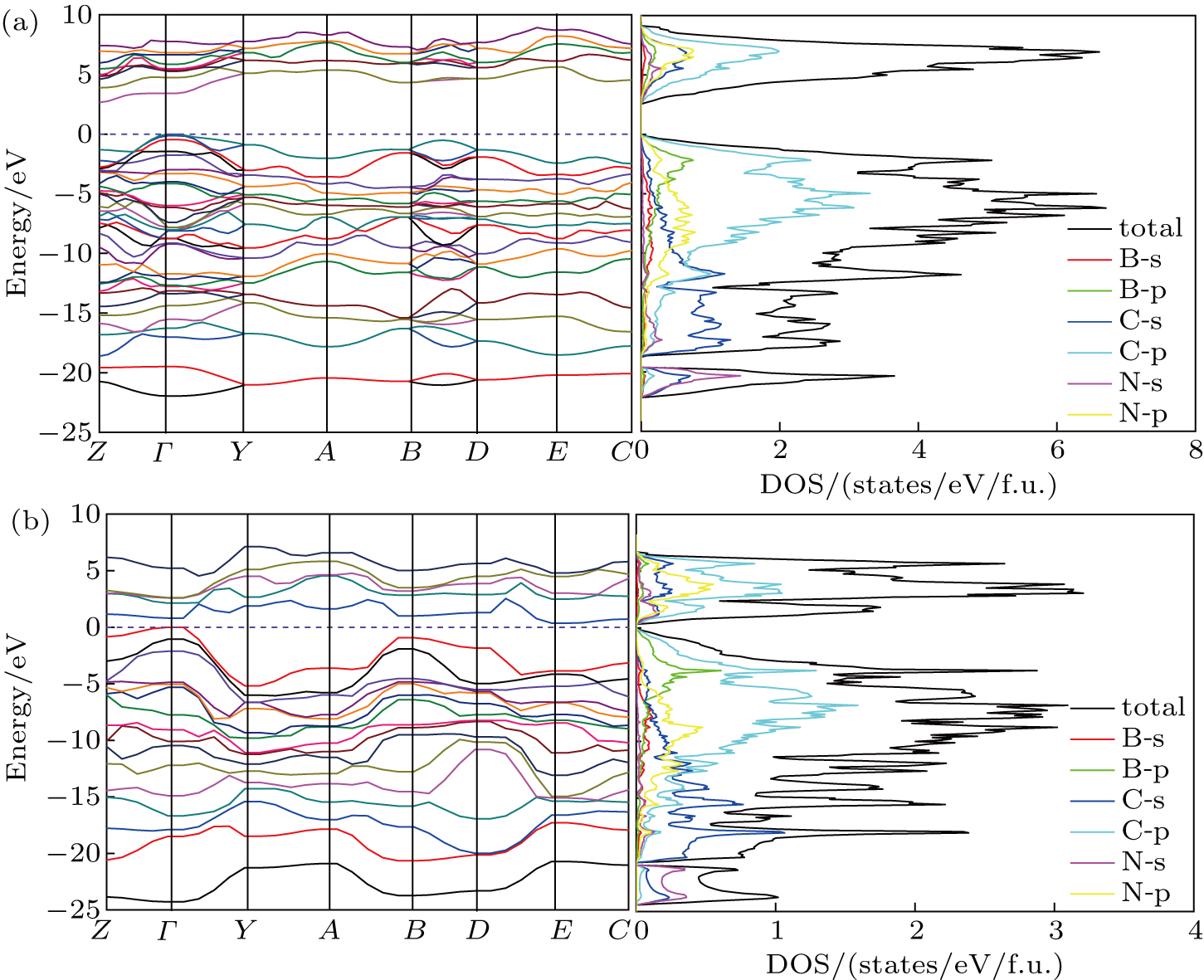 | Fig. 5. Electronic band structures (left panel) and density of states (right panel) of (a) Cm-BC6N and (b) Pm-BC6N. The energy is measured from the valence top. |
To further understand the chemical bonding and electronic properties, we calculate the partial density of states (PDOS) of Cm-BC6N and demonstrate the primary valence-electron states of B, C, and N atoms. From the right panel of Fig.
We also calculate the ideal strength to connect the atomic level strength under plastic deformation and permanent large strain.[48,49] The calculated tensile stress versus tensile strain of Cm-BC6N, Pm-BC6N, t-BC6N, and r-BC6N are shown in Fig. 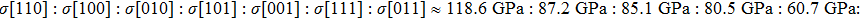
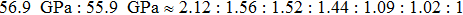
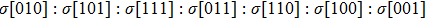
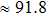
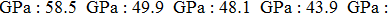
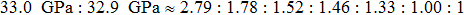
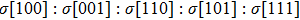
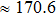
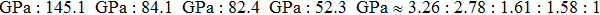
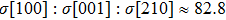
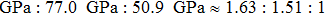
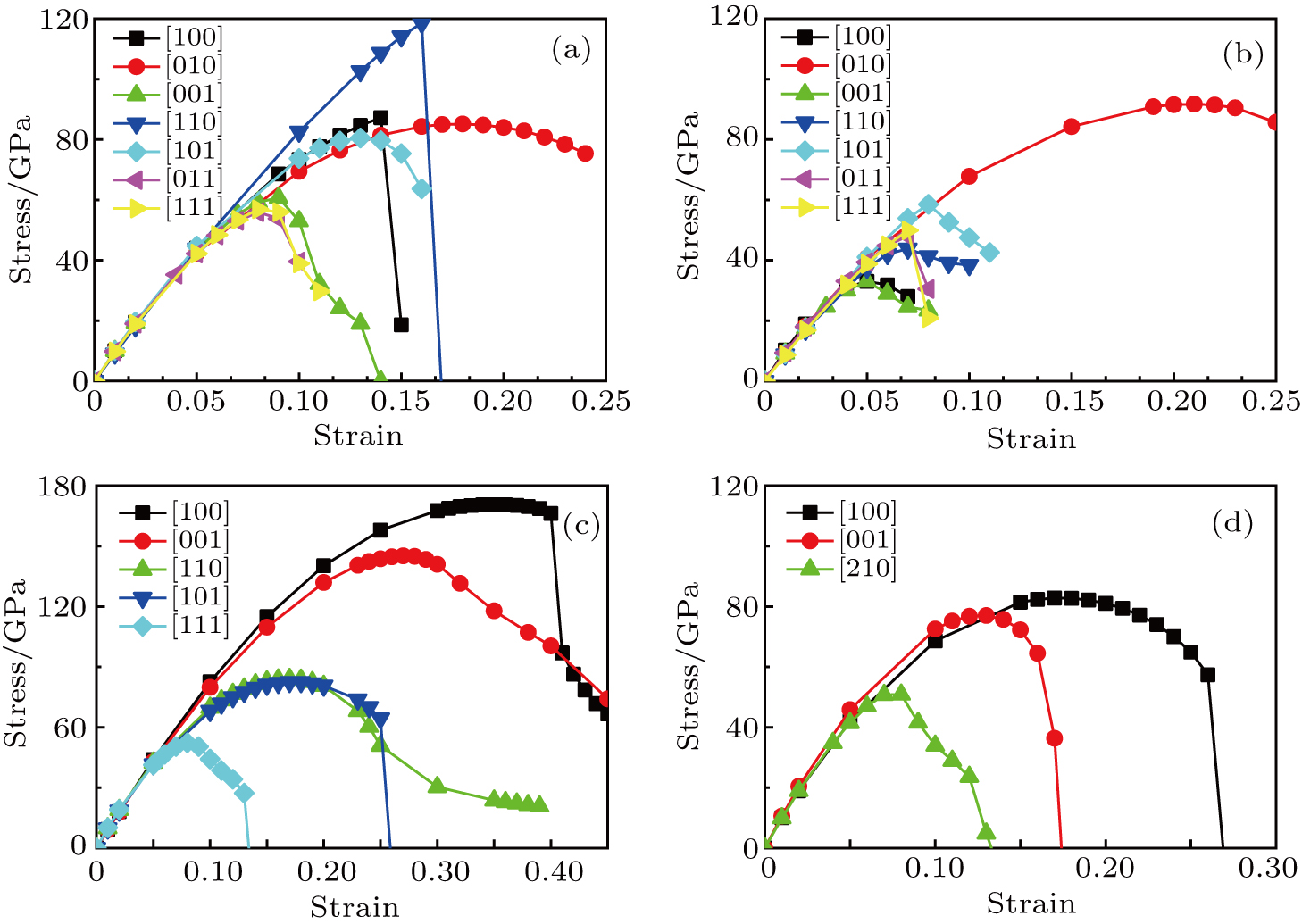 | Fig. 6. Calculated tensile stress versus tensile strain for (a) Cm-BC6N, (b) Pm-BC6N, (c) t-BC6N, and (d) r-BC6N in principal symmetry directions. |
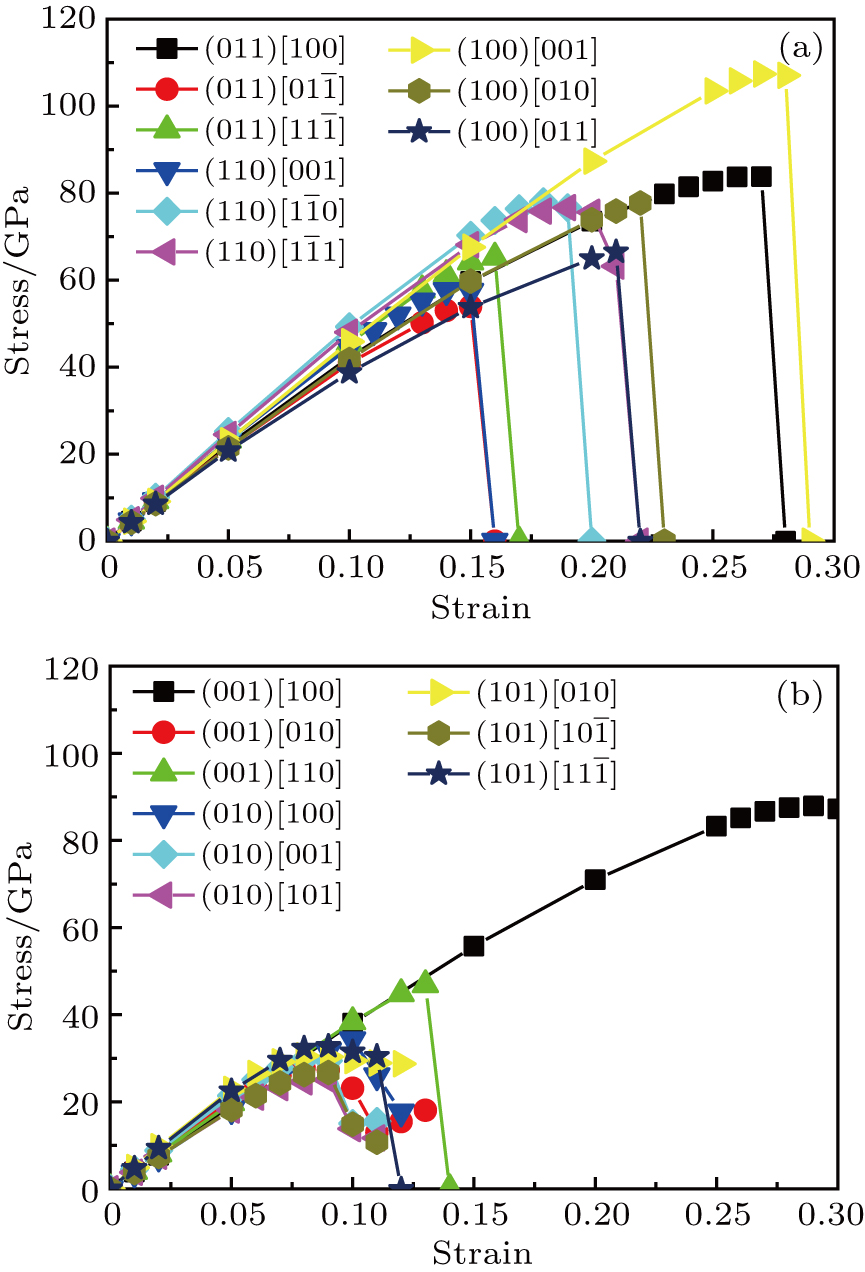 | Fig. 7. Calculated shear stress versus shear strain for (a) Cm-BC6N and (b) Pm-BC6N in principal symmetry directions. |
We also investigate the stress–strain relations of Cm-BC6N and Pm-BC6N in various principal symmetry directions under shear deformation. The anisotropy ratio of the ideal shear strengths for Cm-BC6N is 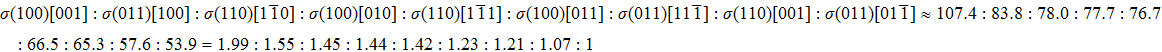
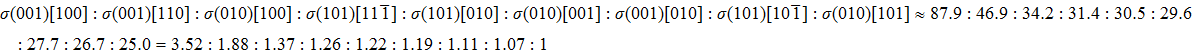
Due to the connection of the hardness and the bulk modulus or shear modulus, we can acquire the hardness. The hardness calculations are performed based on the microscopic models of hardness constructed by Gao et al.[41–43] and Chen et al.[52,53] respectively, which have been widely applied currently. In Gaoʼs microscopic hardness models, the hardness of a covalent material is determined by two factors: the properties of bonding at equilibrium and the number of bonds per unit area. The later includes the bond length, charge density, iconicity, etc. The Vickers hardness 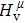
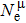
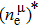
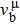
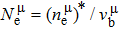
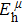
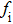
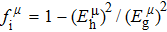
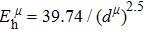
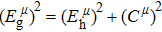
In practical applications, we define the geometric average hardness of all kinds of chemical bonds in crystals as follows:
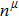
We calculate the atomic bond hardness of BC6N and show the result in Table 

| Table 3.
Hardness calculations of Cm-BC6N, Pm-BC6N, t-BC6N, r-BC6N, c-BC4N, c-BN, and diamond, where |
In summary, two surperhard BC6N with monoclinic structures were proposed. The structural, electronic, and mechanical properties were investigated by first-principles calculations. Cm-BC6N and Pm-BC6N are both mechanically and dynamically stable, and Cm-BC6N is suggested to be more easily synthesized than Pm-BC6N, t-BC6N, and r-BC6N. We found that the lowest stress peak of Cm-BC6N is 53.9 GPa, which is higher than that of other general hard materials. Comparing with other BCN allotropes which have been proposed and Pm-BC6N, Cm-BC6N has a higher hardness from Gaoʼs model (80.6 GPa). In Cm-BC6N, the B and N atoms connect each other by the prominent and strong C–C bond which results in its superior mechanical properties. Both of Cm-BC6N and Pm-BC6N are significantly harder than β-BC2N and c-BN, suggesting the intrinsic superhard materials.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] |