† Corresponding author. E-mail:
It is well known that the radiation efficiency of an acoustic dipole is very low, increasing the radiation efficiency of an acoustic dipole is a difficult task, especially in an ordinary waveguide. In addition, current acoustic superlenses all utilize in-phase sources to do the super-resolution imaging, it is almost impossible to realize super-resolution imaging of an acoustic dipole. In this paper, after using the Helmholtz resonator arrays (HRAs) which are placed at the upper and lower surfaces of the waveguide, we observe a large dipole radiation efficiency at the certain frequency, which gives a method to observe an acoustic dipole in the far field and offers a novel model which is promising to realize the superlens with a source of an acoustic dipole. We discuss how the arrangement of HRAs affects the transmission of the acoustic dipole.
Acoustic dipole is two point sound sources that are very close to each other and have the same amplitude of vibration but with opposite phases. For the same sound intensity, the sound pressure generated by an acoustic dipole is much smaller than that of an acoustic monopole, and the sound radiation power is proportional to the square of the sound pressure amplitude, so the radiation efficiency of the acoustic dipole is very poor. From this point of view, the wave induced by the acoustic dipole can also be regarded as an evanescent wave. However, due to its directivity characteristic, it is widely used in medical sensor and noise control research.[1,2] Helmholtz resonator (HR) has been widely used in acoustic metamaterial structures.[3–11] Because of its special acoustic properties at the resonance frequency, a Helmholtz resonator array (HRA) can turn a normal acoustic boundary into a negative impedance boundary[8] and make the effective modulus of the material change from positive to negative.[11,12] Thus, the properties of unconventional acoustic materials and phenomena such as acoustic cloak can be obtained.[13,14] The existing acoustic superlenses are all using in-phase sources,[15–24] if the acoustic dipole is used as the sound source, there is no doubt that more acoustic information can be achieved when excited with identical sound energy at the same time so that the imaging efficiency can be enhanced. Meanwhile, subwavelength propagation is to be seen by using the resonance propagation characteristics of the HR, which is conducive to the miniaturization of acoustic superlenses. If the method can be used to solve the problem of low transmission efficiency of the acoustic dipole, it is quite promising to realize the acoustic superlens of an acoustic dipole. In this paper, we propose a three-dimensional (3D) waveguide tube with HRAs placed at the upper and lower surfaces, which can enhance the transmissivity of a dipole source greatly.
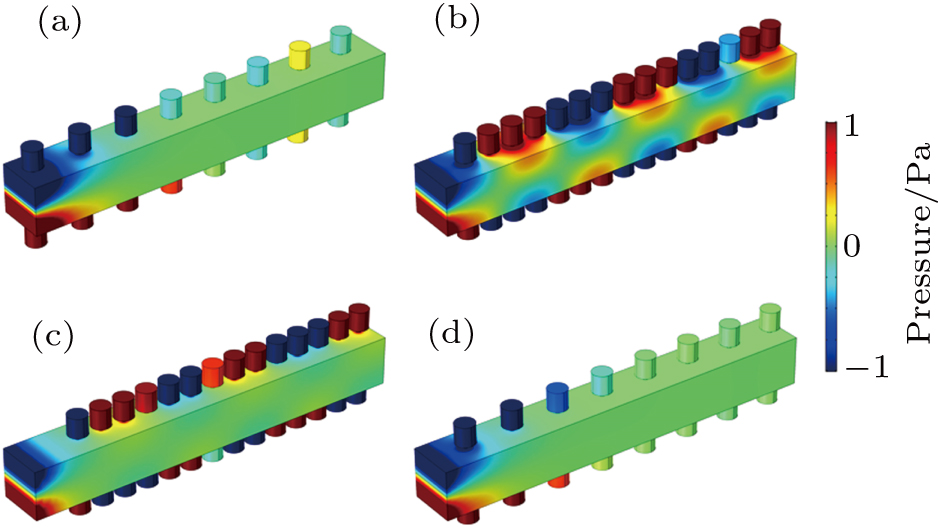
In order to improve the transmission of a dipole source, a structure consisting of a waveguide with symmetric HRAs is designed. We use finite element simulation software COMSOL to simulate the situations when the wave from a dipole-like source propagates through different waveguides without and with HRAs by sweep-frequency method. Left ends of both waveguides are set as dipole-like incident waves whose initial sound pressures of upper and lower parts are −1 Pa and 1 Pa. Right ends of both waveguides are set to the plane wave radiation boundary in order to avoid reflection and two boundary probes are set to monitor the sound pressure lever (SPL) in far fields. All the other boundary conditions of both waveguides are unified as hard boundaries and the background medium is air. As shown in Fig.
Because of the HRAs, the antisymmetric-like mode of transmission in the waveguide can be realized at 5160 Hz. From Fig.
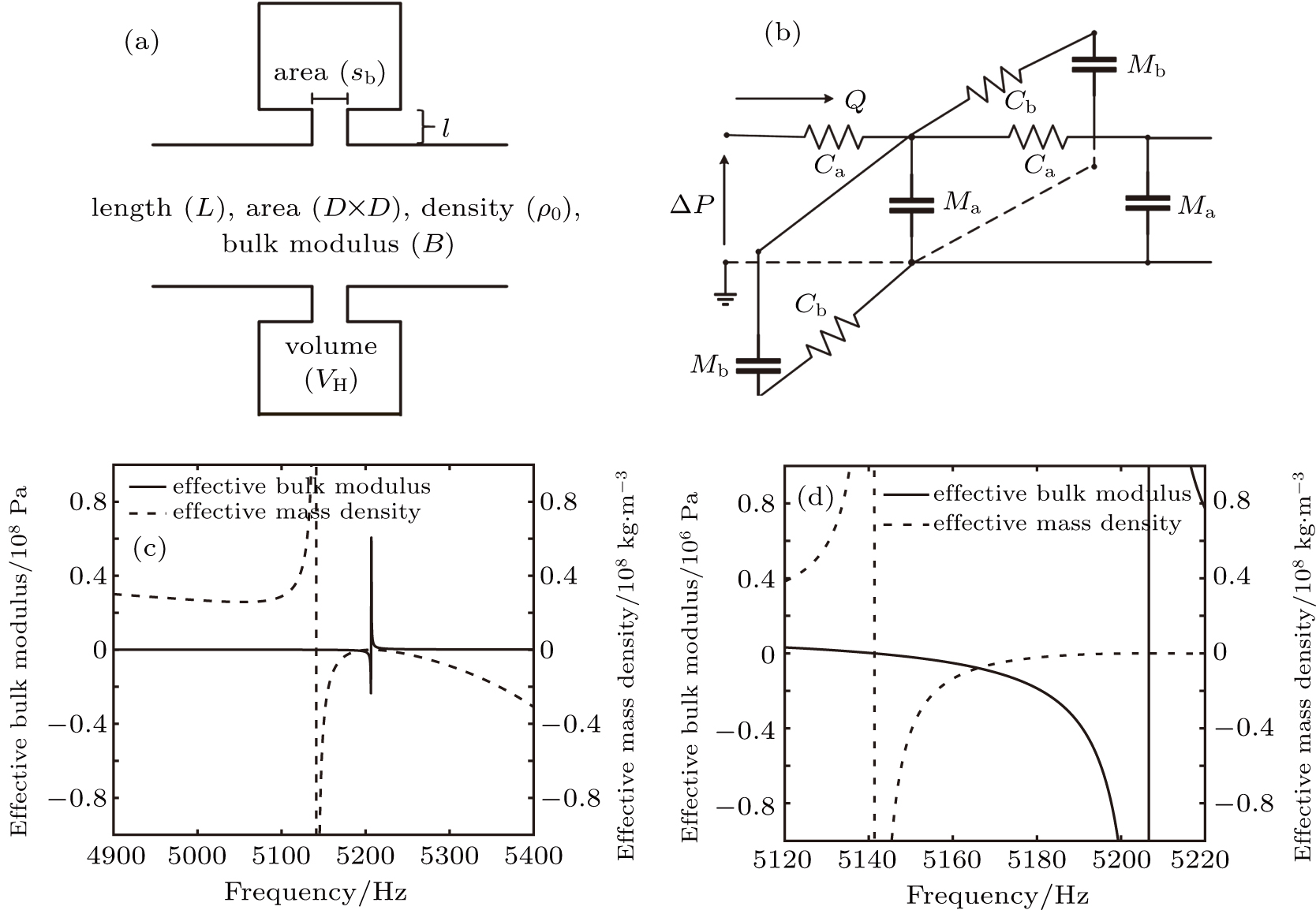
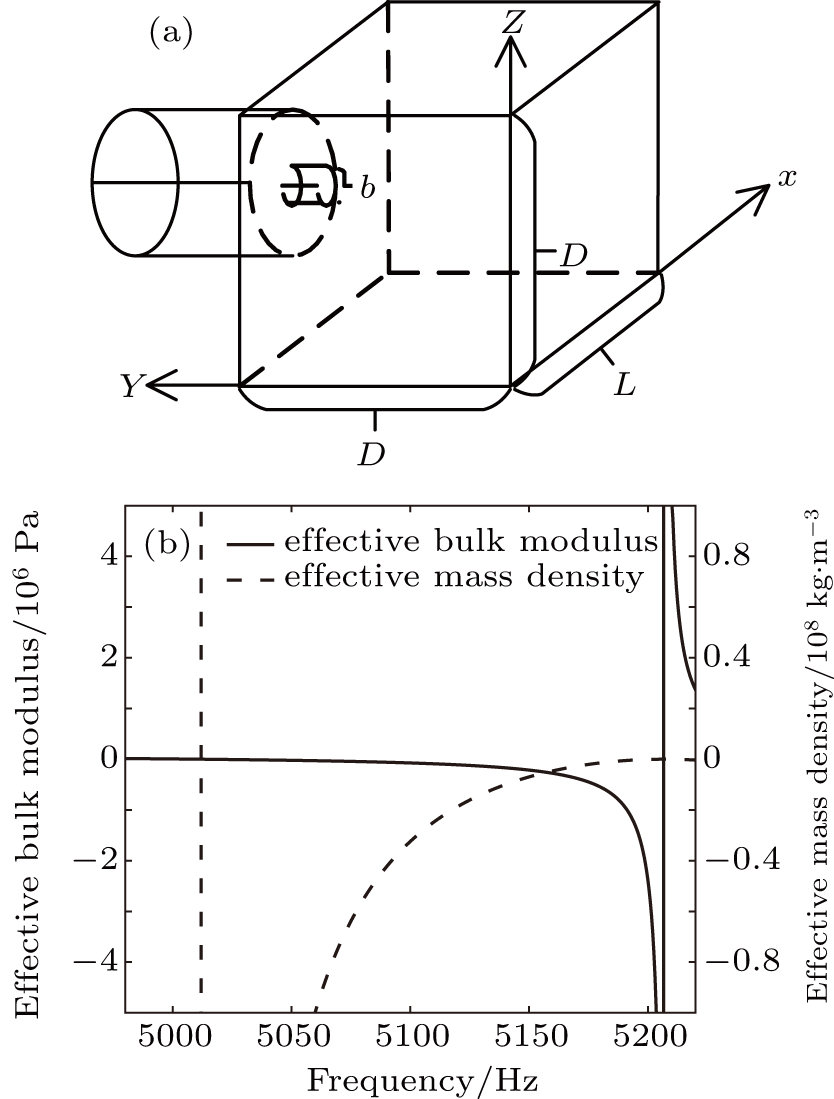
In order to explain the phenomenon, we use electro–acoustic analogy to analyze it. A unit cell is demonstrated in Fig. 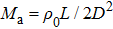
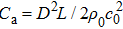
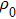
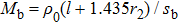
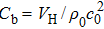
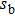
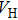
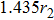
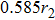

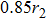
From Fig.
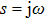
Similarly, we can obtain the equivalent impedance of the Helmholtz resonator
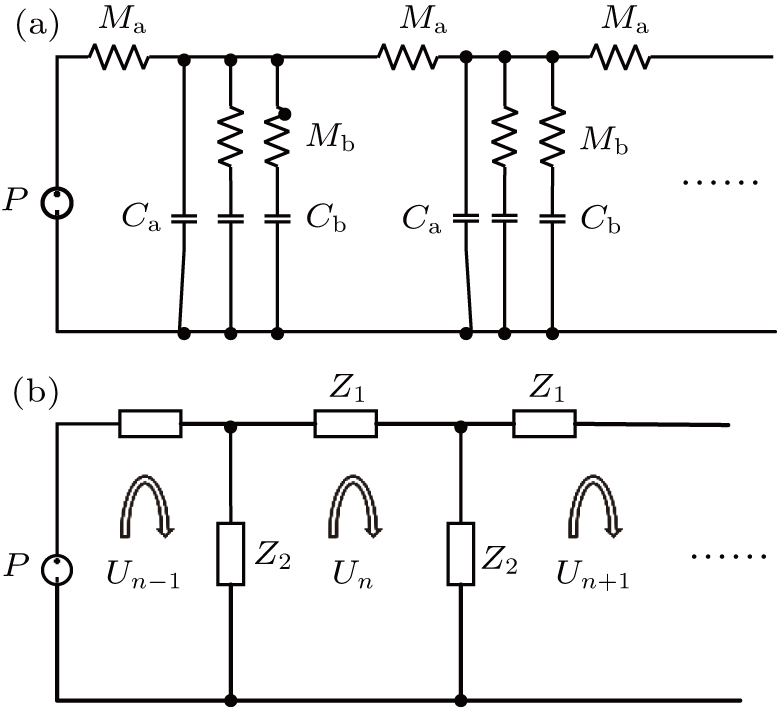 | Fig. 3. (a) Electro–acoustic analogy of the waveguide with HRAs at the upper and lower surfaces of the waveguide and (b) the simplified electro–acoustic analogy. |
In this case, the structure satisfies the situation 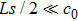
The acoustic volume flow rate in the waveguide can be given as

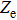
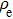
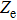
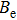
From another perspective, figure 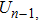

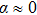
Therefore the respective impedances must satisfy the following inequality:
That is to say, the waveguide with HRAs is equivalent to a bandpass filter at the resonance frequency of the HR. It explains why the two columns HRAs at the upper and lower surfaces of the waveguide can greatly increase the transmittance of the acoustic dipole at the frequency slightly below the resonance frequency of the Helmholtz resonator. Combined with the frequency band of double-negative area, the waveguide with HRAs can be seen as a narrow-band acoustic filter.
Next we will discuss how the arrangement of HRAs affects the transmission of the acoustic dipole. By changing the initial position and period of HRAs, we exam whether the dipole wave can still propagate in the waveguide. To explore this problem, we do the following simulation. By comparing with Fig.
To enhance the transmittance of an acoustic dipole, a waveguide with two columns of HRAs at the upper and lower surfaces of the waveguide is proposed in this paper. By means of electro–acoustic analogy, a good explanation why the dipole wave can only be propagated to far field at the frequency below the resonance frequency of the HR is proposed. A double-negative area is present at the frequency slightly below the resonance frequency of the HR. It is found that the first position of the HRAs and the period of the HRAs have much to do with the transmittance. If the first position of the HRAs is too far away or the period of the HRAs is too large, it will cause the reduction of the attraction of the sound energy or the decline of the coupling intensity, which leads to the inability of the propagation of the wave. If the period is not matched with the half-wavelength of the sound wave, the wave shape distortion may occur although it can be transmitted. In conclusion, with proper first position and period of HRAs, HRAs at the surfaces of the waveguide can greatly improve the dipole transmission efficiency, which is fairly promising for the future application to acoustic superlenses.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] |