† Corresponding author. E-mail:
A comparison of differently polarized Bessel vortex beams propagating through a uniaxial anisotropic slab is discussed in terms of the vector wave function expansions. The magnitude profiles of electric field components, the transformation of polarization modes, and the distributions of orbital angular momentum (OAM) states of the reflected and transmitted beams for different incident angles are numerically simulated. The results indicate that the magnitude profiles of electric field components for different polarization modes are distinct from each other and have a great dependence on the incident angle, thus the transformation of polarization modes which reflects the change of energy can be affected largely. As compared to the x and circular polarization incidences, the reflected and transmitted beams for the radial polarization incidence suffer the fewest transformation of polarization modes, showing a better energy invariance. The distributions of OAM states of the reflected and transmitted beams for different polarization modes are diverse as well, and the derived OAM states of the transmitted beam for radial polarization present a focusing effect, concentrating on the state between two predominant OAM states.
The vortex beams carrying orbital angular momentum (OAM)[1] have been widely studied over a few past decades, including generation,[2,3] characteristics,[4–6] and applications in optical communication,[7] imaging,[8] micro-particle manipulation,[9] etc. In particular, the different OAM states are mutually orthogonal while propagating coaxially and thus promote potential applications in improving the capacity of communication systems. Gibson et al. implemented the initial demonstration of using OAM for free-space communication, experimentally proving the possibility of transmitting information by vortex beams.[10] The team led by Wang has been working on the multiplex/demultiplex of OAM in the optical band and has obtained several valuable research results.[11,12] Appreciable literatures on the transmission efficiency,[13–15] the security performance,[16] and the mitigation of crosstalk[17] of vortex beams have been reported. Some other researches which are worth mentioning also boost the development of vortex beams in quantum communication,[18] RF communication,[19] and material processing.[20] Whereas, the propagation of vortex beams in media inevitably results in the distortion of electric field amplitude and further causes the crosstalk of OAM states.[21] Such distortion is even serious in anisotropic media because of the double refraction behavior. Yu[22] and Wang[23] studied the propagation of Airy Gaussian vortex beams and chirped Airy vortex beams in uniaxial crystals, respectively. The results prove that the ratio of extraordinary and ordinary refractive indices affects the asymmetry of the intensity a lot. As a kind of typical anisotropic media, uniaxial anisotropic media are widely applied in optical signal processing,[24] optical element design,[25] and manufacturing of microwave devices.[26] Exploring the variations of field profile, polarization mode, and OAM state of the reflected and transmitted beams during the propagation of vortex beams in uniaxial media can potentially improve the quality and efficiency of practical applications.[27]
Compared to other vortex beams, Bessel vortex beams[28] whose electric field intensity is independent of propagation distance are treated to be more advantageous for long-distance communication,[29] optical imaging,[30] and other applications[31,32] since its field profile can self-reconstruct after passing through obstacles. Besides, such diffraction-free beams suffer less power loss than Gaussian beams,[33] which means a higher signal-noise ratio in practical optical communication. With the need of large data transmission for optical communication, according to the Fresnel–Arago interference law,[34] the general way is to use the same information-carrying beams with two orthogonal linear polarization modes at the input of an optical communication system to provide twofold data channels.[35] However, it will lower the transmission efficiency of communication systems because there must be corresponding polarizers at the receiving end to decode the information carried by beams with different linear polarization modes. A high extinction ratio polarization beam splitter skillfully utilizing the displacements of TE- and TM-polarized beams in a low-symmetric photonic crystal was designed to simplify the optical communication system in the precondition of high transmission efficiency.[36] Furthermore, Quabis et al. found that the radially polarized beams have the favorable focusing characteristic which could be used to build improved near field sensors.[37] Generally speaking, the polarized Bessel vortex beams (PBVBs) which simultaneously possess the polarization characteristics and OAM properties are potential to increase information capacity and transmission efficiency by combining with the polarization–division multiplexing (PDM) and mode–division multiplexing (MDM) systems. However, in this case, the distortion of electric fields and the crosstalk of OAM states stemming from the transformation of polarization modes need to be taken into account. As far back as 2001, Nesterov and Niziev had investigated the propagation characteristics of beams with axially symmetric polarization, finding that such polarized beams are free from polarization aberrations.[38] King also found the derivation of topological charge of a circularly polarized Bessel vortex beam in biaxial crystals and demonstrated the transformation of a Bessel beam from zeroth to first order and then from first to second order.[39] Furthermore, the oscillating polarization along the optical axis of Bessel beams in free space was discussed by Fu and his co-worker.[40] It seems that the influence of polarization mode on the propagation of a Bessel vortex beam is still worth considering for further understanding, especially in the communication systems involving both polarization–division multiplexing and OAM–division multiplexing.
In this paper, the comparison of three kinds of polarized Bessel vortex beams incident on a uniaxial anisotropic slab is investigated by use of the cylindrical vector wave function expansions and the eigen plane wave spectrum representation. The paper is arranged as follows: section
The sketch of an arbitrary polarized Bessel vortex beam which is obliquely incident on a uniaxial anisotropic slab is shown in Fig. 
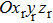


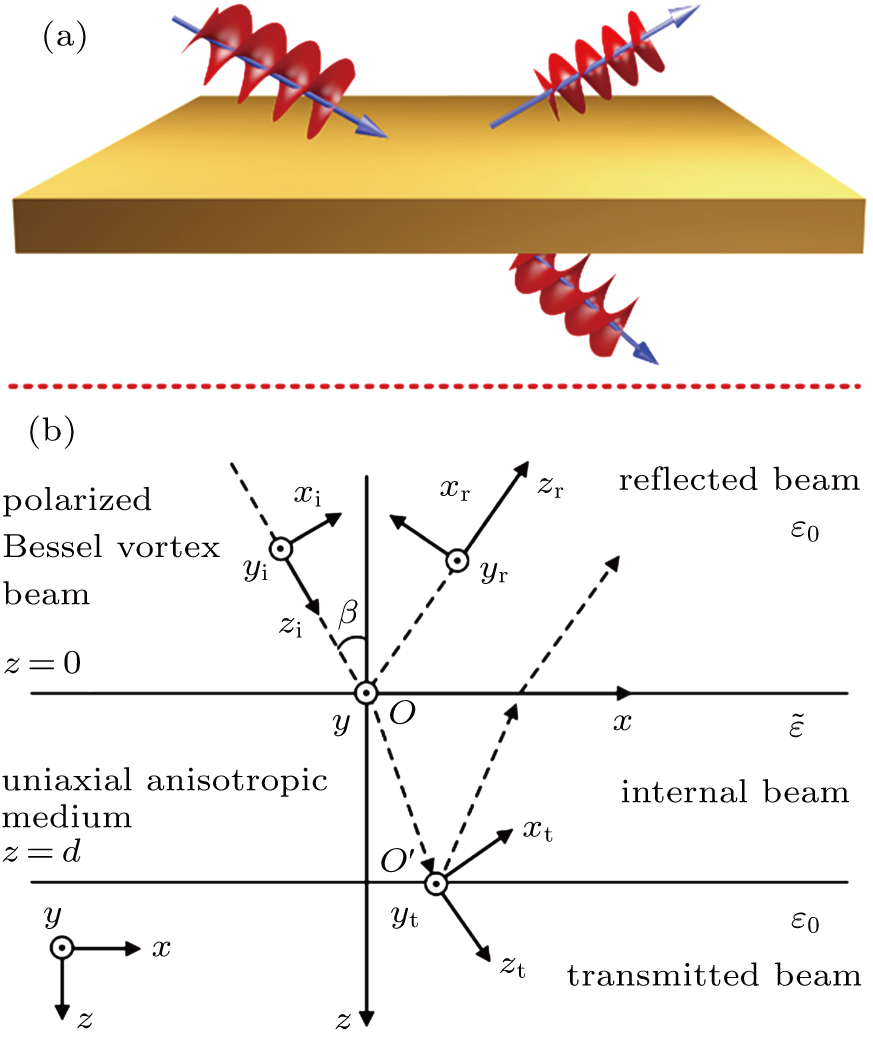 | Fig. 1. Oblique incidence of an arbitrarily polarized Bessel vortex beam on a uniaxial anisotropic slab. |
According to the angular spectrum decomposition (ASD) method, the electric and magnetic field vectors of a polarized Bessel vortex beam under the incident coordinate system 
 |
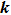
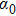
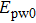
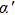
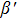
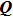
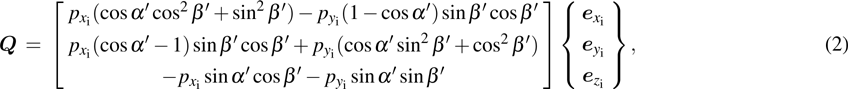 |


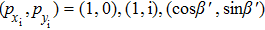
By expanding the factor 
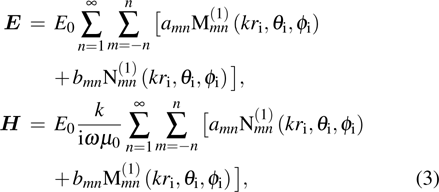 |
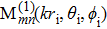
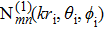
 |
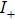
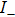
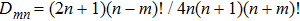
Considering the incident angle β, by utilizing the addition theorem of the SVWFs, the electric field vector of the incident beam can be expressed under the global coordinate system Oxyz as[44]
 |
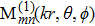

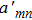
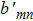
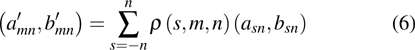 |
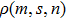
According to the transformation relationship between the SVWFs and the CVWFs,[44] equation (
 |
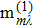
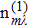
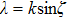
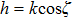
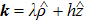
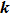
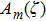
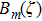
 |
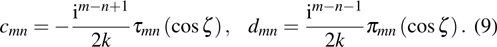 |
The corresponding expansion for the magnetic field vector can be obtained by Maxwell equations.
Let us consider the actual incidence of a PBVB which can be interpreted as the superposition of plane wavelets. Under this proposition, only the plane wavelets which illuminate on the upper surface of the slab are considerable, which means that the integration interval of ζ in Eq. (
Similarly, the electric field vectors of the reflected and transmitted beams are as follows:
 |
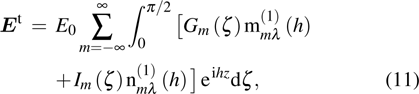 |
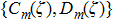
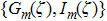
The electric field of the internal beam in a uniaxial anisotropic slab whose optic axis is perpendicular to the upper surface (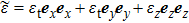
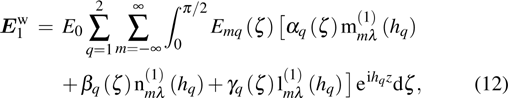 |
 |
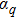
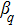
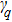
Through the electromagnetic fields boundary conditions that the tangential components of the electromagnetic fields are continuous, a set of simultaneous equations can be obtained, from which the expansion coefficients and then the corresponding field components can be solved numerically.
To analyze the effects of such media on the transformation of polarization modes during the propagation of a PBVB, the following expression[47] which is similar to the definition of the polarization extinction ratio (PER) is used to investigate the polarization characteristics of the reflected and transmitted beams:
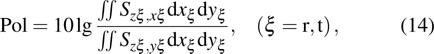 |
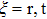
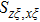

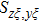
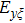
Similar to the angular spectrum decomposition, vortex beams can be interpreted as the superposition of infinite spiral harmonics 
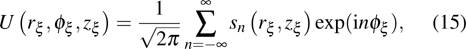 |

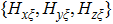
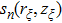
 |
As we all know that the time-averaged energy density of a beam is 
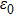

 |
To intuitively analyze the influence of the incident angle and polarization on the deformations of the electric field amplitude and OAM state, as well as the transformation of polarization mode, numerical simulations are given below by using the theoretical formulae derived in section 


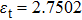

Figure 


 | Fig. 2. Magnitude profiles of the electric field components of incident beam for different polarization modes. |
As we can see from Fig. 



The magnitude profiles of electric field components of the reflected beam for different polarization modes are displayed in Figs. 

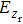
 | Fig. 3. Magnitude profiles of the reflected electric field components for the x polarized incidences. |
 | Fig. 4. Magnitude profiles of the reflected electric field components for the circularly polarized incidence. |
 | Fig. 5. Magnitude profiles of the reflected electric field components for the radially polarized incidence. |
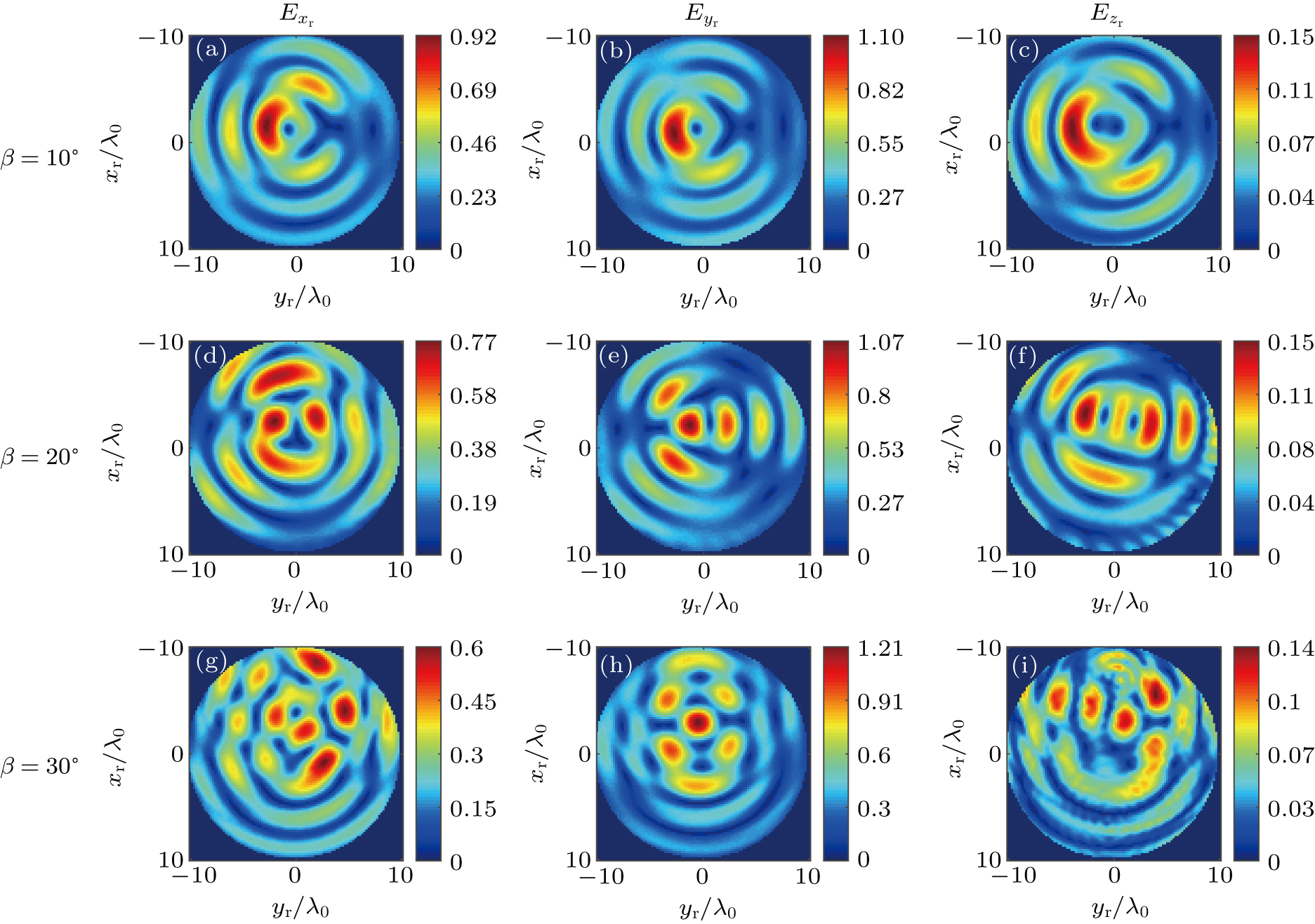
It can be seen from Figs. 
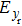

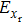
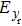
Compared to the circular polarization incidence, the difference between the maximum values of the transverse electric field components 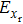

Similarly, the magnitude profiles of electric field components of the transmitted beam are presented in Figs. 


 | Fig. 6. Magnitude profiles of the transmitted electric field components for the x polarized incidence. |
 | Fig. 7. Magnitude profiles of the transmitted electric field components for the circularly polarized incidence. |
 | Fig. 8. Magnitude profiles of the transmitted electric field components for the radially polarized incidence. |
Just as the behaviors of reflected field components, the magnitude profiles of the transmitted field components also have distortions. Comparing with the incident beams, the central circular rings in the contours shown in Figs. 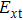

To have a clear understanding about the variations of the polarization of the reflected and transmitted beams, the value of Pol by Eq. (
In order to provide a reference for comparison, the polarization patterns of the incident beams are presented in Fig.
 | Fig. 9. Polarization patterns of the incident beam: (a) x polarization; (b) circular polarization; (c) radial polarization. |
Figure
Figure
It can be seen from Figs.
Tables
| Table 1.
Pol of the reflected beam with different incident angles. . |
| Table 2.
Pol of the transmitted beam with different incident angles. . |
It reveals in Tables 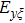
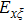

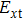
The transformation of polarization modes finely reflects the energy transfer along the polarization directions. However, for practical applications of vortex beams, the investigation into the energy of each helical harmonic is important as well, especially in an OAM multiplexing system. To analyze the effects of polarization modes and incident angles on the deformation of OAM states, figures
Figures 
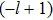

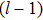
The reflection and transmission of a PBVB by a uniaxial anisotropic slab had been investigated by use of the cylindrical vector wave function expansions. The electromagnetic fields of the incident, reflected, and transmitted beams, as well as their corresponding expansion coefficients, were obtained utilizing the CVWFs. The magnitude profiles of the field components, the transformation of polarization modes, and the distributions of OAM states of the reflected and transmitted beams were analyzed in detail. The results indicated that the magnitude profiles of the reflected field components were more obviously complicated than those of the transmitted field components, and their contours are seriously distorted as the incident angle increases. Compared to x and radial polarization incidences, the reflected beam for the circular polarization incidence had the minimum transformation of polarization modes between the transverse electric field components. Although the magnitude profiles of the reflected field components for three kinds of polarization modes were in wild disorder with a bigger incident angle, the energy of the reflected beam seemed to go back to the predominant OAM states. Different from the cases of x and circular polarization incidences, the derived OAM states in the transmitted beam for the radial polarization incidence located at the OAM state between its two predominant OAM states, leading to the focused effect of OAM state. The results in this paper may provide some supports in the design of optical devices and the OAM multiplexing communication combining with a polarization–division multiplexing segment.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] |





