Atoms and molecules driven by intense laser pulses radiate high-order harmonics generation (HHG) whose frequencies are integer multiples of the incident laser frequency. HHG is a promising method to produce a unique table-top source of coherent x-ray and attosecond pulses for ultrafast spectroscopy.^[1] The physical mechanism behind HHG has been clearly declared by the classical three-step model.^[2] Step one: the electron is liberated by tunneling from the potential barrier that built by the collaboration of atomic potential and the electric potential of laser field. Then step two, the electron oscillates in the laser field, and gains large amount of kinetic energy (from 1 to hundreds of photons) from the laser field. Finally, in the step three, the electron recombines with the parent ion and releases the gained energy by radiating a harmonic photon.

Symmetry plays an important role in the HHG of atomic and molecular systems. If the medium (atom or molecule) is inversion-symmetric, such as an atomic or non-oriented molecular gas, the suppression of even-harmonics has been certified,^[3] only odd harmonics can be observed in experiments.^[4–6] The absence of even-harmonics can be explained by the concept of inversion symmetry. In the quantum system with a center of inversion symmetry, the parity of the systemʼs eigenstates must be +1 or −1. In the view point of perturbation theory, the cause and mechanism of the n-th order HHG can be treated as follows: absorbing n photons of laser frequency and then releasing a harmonic photon. Since the transition between two states must be different parity, therefore, an even number of photons could not be absorbed by the system. This is why the atoms could not produce even-harmonics, i.e., even-harmonic generation is absolutely forbidden in atoms. More details by studying the symmetry properties to obtain the selection rules for even and odd harmonics can be found in Refs. [3] and [7]. In an ensemble of oriented diatomic molecules, except the homonuclear molecules, the inversion symmetry is broken. It has been predicted that the even-harmonic generation in the asymmetry molecules shined by laser field.^[8–11] There are plenty of investigations on the selection rules^[12,13] and applications^[10,14,15] on the even harmonics of asymmetric molecules.

In recent years, people focus on HHG in a spatially inhomogeneous field^[16–18] produced by a metal nanostructure when it is illuminated by a short laser pulse. By using such an inhomogeneous field, relying on the strong confinement of plasmonic hot spots, HHGs in nanostructures show a lot of novel characteristics, such as extending the harmonic cutoff energy^[17,19–22] and increasing the harmonic yield.^[23,24] Moreover, the isolated attosecond pulse has been proposed to generate by selecting the quantum path with inhomogeneous fields. Those characteristics just fit one of the most major branches of HHG studies. On the other hand, Ciappina et al. observed the generation of even-harmonics within inhomogeneous field of single-tip nanostructure.^[25] To understand how the induced inhomogeneous field plays its role in even-harmonics generations, in this work, we performed a theoretically numerical analysis to investigate the HHG from a hydrogen atom in two different types of spatially inhomogeneous field. By comparing HHG spectra in two kinds of inhomogeneous field which generated by bow-tie and single-tip nanostructures respectively, we will discuss how the inhomogeneous field produces modifications in the harmonic periodicity, and reveal the mechanism of even-harmonics generations by laser-induced inhomogeneous field. By analyzing the HHG process using time-frequency and semiclassical calculations, we present strong evidence about the atomic even-harmonic generation due to symmetry-breaking effects induced by the spatially inhomogeneous field. Unless specifically stated otherwise, the atomic units (a.u.) are used throughout this paper.

To fully describe the HHG process in quantum mechanics, it is required to solve the three-dimensional (3D) time-dependent Schrödinger equation (TDSE). However, the previous investigation on simulations of one-dimensional (1D) and 3D TDSEs shows that the harmonic spectra and the positions of the cutoff are remarkably similar.^[26] Therefore in this work, we will perform the simulation of HHG process from a hydrogen atom in a spatially inhomogeneous field by solving the 1D TDSE in length-gauge

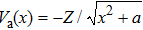
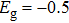
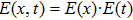
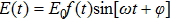
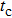
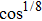
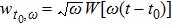
In this section, the effect of electric field inhomogeneity on the spectral profile of the high-order harmonic spectrum will be discussed. We have calculated the HHG spectra of hydrogen atoms emitted by two kinds of inhomogeneous field which generated by the bow-tie [Fig. 1(a1)] and the single-tip [Fig. 1(a2)] nanostructure, respectively. The typical intensity of the inhomogeneous field is taken to be 70 TW/cm², the laser pulse has a Gauss-shaped envelope and total duration of 10 optical cycles (o.c.), the CEP φ of driving field is 0. Spatial function of two fields are expressed as (i) bow-tie: and (ii) single-tip: . The value of the parameter ε is 0.06. Figure 1(a1) and 1(a2) show the scheme of two systems considered in our paper, and different gold nanostructures result in great differences in the space-varying electric field. The behaviors of the corresponding resonance-enhanced electric fields are significant divergence in one optical cycle (black square zone). Axial symmetry and inversion symmetry of space are distinctly shown in Figs. 1(b1) and 1(b2), respectively. Briefly, in the case of bow-tie nanostructure, the electric field at and has the same sign for a fixed time t in Fig. 1(b1), i.e. , which can characterize the symmetrical spatial inhomogeneity. However, figure 1(b2) displays different electric fields at and , i.e., .

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Interaction scheme considered in this work: a few-cycle 800-nm laser beam is focused into a gold bow-tie nanoantenna (a1) or a single nanotip (a2), and (b1), (b2) corresponding induced fields, respectively. (c) Harmonics are generated from hydrogen atom by two kinds of enhanced driving field and homogeneous field.

Figure 1(c) shows harmonic spectrum obtained from a hydrogen atom under the irradiation of bow-tie (black dashed-dotted curves) and single nanotip (red curves) inhomogeneous fields, respectively. The cyan dashed curves are plotted as a comparison without inhomogeneous field. Due to different field enhancements by two nanostructures, the harmonic efficiency of black line is higher than the red one for the high-order harmonics. We can notice the enhanced harmonic (black curve) and an extra peak at the harmonic order. The subtle structure of greater differentiation between two spectra are shown in the subgraphs. Pure odd-harmonic generation (black curve) occurs when the bow-tie nanostructure is utilized. However, a comb of well-resolved odd and even harmonics appears in the red curve of single-tip case. Even-harmonic which has the same order of magnitude as the odd ones can be distinctly found in the harmonic emission spectrum (red dotted curve).

For both kinds of inhomogeneous field, it can be seen that an apparent peak–valley structure appears in the harmonic spectrum. To clarify the peak–valley structure and illustrate the dynamics from the harmonic platform in two inhomogeneous fields, we employed the wavelet transform of time-dependent induced dipole acceleration. First, for comparison, in Figs. 2(a1) and 2(a2), we show the transient information of harmonic emission and classical kinetic simulation with homogeneous field. We can only observe HHGs at very low orders. Then, in Figs. 2(b1) and 2(c1), we show the transient information of harmonic emission of each kind of inhomogeneous field. As expected, the main contribution to the harmonic signal comes from the central part of a laser pulse whose intensity is the strongest. As we can see, for two different inhomogeneous cases, the time–frequency spectra are very distinctive. In Fig. 2(b1), the bow-tie inhomogeneous field, same as the homogeneous field, two light emissions can be found in each optical cycle. However, in Fig. 2(c1), the single nanotip case, only once light emission appears. According to three-step model,^[2] the tunneled electron could be treated as classical particle. As it is shown in Figs. 2(b2) and 2(c2), we also calculate the classical action of the ionized electrons to investigate the origin of the harmonic interference. We describes the motion of an ionized electron in the inhomogeneous field (neglect the influence of the atomic potential) by solving Newtonʼs equation . In our simulation, it is tacitly assumed that the electron leaves the ‘tunnel’ with zero velocity, which means the initial velocity is zero. Also, the position of the ionized electron is set to zero. The time-dependent total energy is equal to the ionized electronʼs kinetic energy plus the ionization energy of the atom. Upon comparing the classical and quantum calculations, as shown in Fig. 2, they agree well with each other. The half-wave symmetry of the time-periodic homogeneous field is expressed by ,^[27] where T is the period of laser field. By that analogy, the electron density of the quantum system in homogeneous field is , which provided the initial field-free state possesses the inversion symmetry. This initial field-free state makes constructive interference appear on odd-harmonics and destructive interference of even-harmonics. Pure odd-harmonics show up when atom is illuminated by homogeneous field. In two systems of our simulation, axial symmetry and inversion symmetry of spatially inhomogeneous fields are distinctly as shown in Figs. 1(b1) and 1(b2), respectively. The introduce of spatial inhomogeneity of the electric field reinforces the modulation of the electric field manipulates the electron. For the axial symmetry case, i.e., , as shown in Fig. 2(b1), it emits light twice in a cycle, so the half-wave symmetry plus axial symmetry of inhomogeneous field still works well as homogeneous field of Fig. 2(a1). For the inversion symmetry case, i.e., , generation of even harmonics indicates that it may break inversion symmetry under the influence of the external field, which is equal to the half-wave symmetry plus inversion symmetry of inhomogeneous field.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Wavelet time-frequency spectra (absolute value) of the dipole acceleration and classical kinetic simulation.

To illustrate the possible half-wave symmetry breaking, we have calculated the time-dependent probability to find the electron and analyzed the profiles of the classical trajectories in both cases. Figure 3 shows the results for two inhomogeneous cases where the HHG spectra differ qualitatively. As we can see, in Fig. 3(a), during each period of laser pulse (e.g., between the 4th to the 5th o.c.), the probabilities to find the electron which is back to parent ion in the up half-space and the down half-space correspond to the half-wave symmetry plus axial symmetry: on each half cycle, undergoing the “acceleration–deceleration–reverse acceleration” process, the electron returns the parent ion. This is the same as the homogeneous field of Fig. 3(d). With the single-tip inhomogenous field, as it is shown in Fig. 3(b), the electron plays the same role which in bow-tie inhomogeneous field on first half cycle, but the electron never returns on the second half cycle. In Fig. 3(c), we present electron trajectories of both inhomogeneous fields. Between the time 4 o.c. and 4.5 o.c., we can observe complete trajectories: from the birth time to the first recollision time. They present a striking contrast between inhomogeneous field of bow-tie and single-tip nanostructures. We blame this on symmetry in the total electric field. In another word, the symmetry-breaking effects make it possible that even-harmonic generates when an atom is illuminated by single nanotip spatially inhomogeneous field.

Fig. 3.

Figure Option ViewDownloadNew Window

Fig. 3. Evolution of the electronic wave-packet and classical trajectory analysis (red curves) for (a) bow-tie field, (b) single nanotip field and without nanotip with the same temporal function E(t), respectively. (c) Classical trajectory analysis for bow-tie field (red lines) and single nanotip field (white lines). (d) Electronic wave-packet and classical trajectory analysis (red curves) with homogeneous field.

The HHG processes of hydrogen atoms under the interaction with two kinds of spatially inhomogeneous field were investigated by numerically solving the TDSE. These spatially inhomogeneous fields lie in a vicinity of the metal nanostructure when they are illuminated by ultrashort laser pulses. Due to the effect of inhomogeneity of induced field, the inhomogeneous field produced modifications in the harmonic periodicity. The odd and even-harmonics were both observed in the single nanotip case. The bow-tie nanostructure could produce only odd harmonics, it still follows the same symmetry rules as that of homogeneous field with atomic targets. By employing the classical equation of motion for an electron moving in a linearly polarized inhomogeneous electric field and time–frequency analysis, we demonstrated the origin of even HHG from the symmetry-breaking of the total atom–laser system.