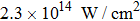High-order harmonic generation (HHG) from intense laser–matter interaction has been proven to be a fruitful method for producing extreme ultraviolet (XUV) coherent light^[1–3] and attosecond pulses.^[4–7] HHG is currently a key technology to obtain tabletop ultrafast short-wavelength laser sources. In the semi-classical picture, HHG can be treated as a three-step process:^[8–10] First, an electron in an atom or molecule is ionized by an intense laser field through tunnel-ionization into continuum. Then, the liberated electron is driven back by the oscillating laser field, which can possibly return to the parent ionic core. Finally, the returned electron could recombine with the ionic core to emit redundant energy as coherent XUV photon flux. The emitted high-order harmonics have been shown to contain the information of the target in sub-femtosecond time scale and sub-nanometer spatial resolution. High-order harmonic spectroscopy has been used to obtain the electronic structure and dynamics of an atom or molecule in intense-field ultrafast processes, including multi-electron dynamics,^[11–13] Cooper minima,^[14,15] and structure interference.^[16–18]

Comparing to atoms, molecules exhibit much more complex phenomena when interacting with strong laser fields due to their diverse geometric and electronic-state structures, as well as additional rotational–vibrational degrees of freedom. These features provide explicitly extra parameters to control HHG or contain more information for imaging molecular orbitals. In recent theoretical^[19,20] and experimental studies,^[17,21–27] the structure and symmetry of molecular orbitals have been revealed through HHG. For instance, the electronic structure of the target molecules can be revealed by observing the minimum of the molecular harmonic spectrum induced by the two-center interference.^[16] By controlling the angle between the molecular axis and the driving laser field, the motion of the electron in ionization and recombination processes could be determined, providing a new opportunity to explore the geometrical structure of the molecular orbitals.

It is reasonable to expect that only the least bound molecular orbital, i.e., the highest occupied molecular orbital (HOMO), would contribute to HHG. In recent years, however, lower lying orbitals have been demonstrated to be involved in the process of HHG, showing multi-orbital effects which are encoded in the harmonic signals. For example, McFarland et al.^[28] investigated HHG of aligned N₂ molecules, showing the contribution of HOMO-1 by measuring the distinct revival structures between the plateau and cutoff harmonics. The contribution of HOMO-1 to HHG of N₂ was further studied by Le et al.^[29] using a quantitative rescattering theory. The results indicated that the contribution of HOMO-1 becomes significant near the cutoff region and depends on the intensity of the driving laser. By measuring the harmonic spectral phase of aligned N₂, Diveki et al.^[30] found that the relative contributions of HOMO and HOMO-1 could be manipulated by adjusting the intensity of the driving laser. Very recently, Troβ et al.^[31] investigated the contribution of multiple orbitals on HHG from aligned N₂ by measuring the revival structure and the angular distribution of harmonic signals.

In this work, we measure the HHG from aligned N₂ molecules irradiated by a linearly or elliptically polarized strong laser field. The harmonic yield is investigated as a function of the angle between the molecular axis and the polarization of the driving laser field. We investigate the ellipticity dependence of HHG from N₂ molecules which are aligned either parallel or perpendicular to the major axis of the polarization ellipse. Based on our experiment results, we discuss the contribution of HOMO and HOMO-1 on HHG in both linearly and elliptically polarized laser fields.

Molecular harmonics were generated and measured by a home-built XUV flat-field grating spectrometer, which has been described in detail in our previous publications.^[32–34] Briefly, the output of a Ti: sapphire laser system (1 kHz, 35 fs, 800 nm) was divided into two laser beams by a beam splitter. One beam with lower energy (the aligning laser) was used to create rotational wave packets to nonadiabatically align the molecules. The other beam with higher energy (the driving laser) was used to produce HHG from the aligned molecules. The diffraction efficiency of spherical grating depends on the angle between the polarization direction of harmonics and the groove of the grating. To minimize this influence, the ellipticity of the driving laser was adjusted by a zero-order half-wave plate placed before a fixed zero-order quarter-wave plate. The half-wave plate was placed on a motorized rotation mount to change the ellipticity (ε) continuously between ε =0 (linearly polarization) and ε =1 (circular polarization). The delay time of the two beams was precisely adjusted by a translation stage. The intensities of the two laser beams were controlled by a half-wave plate and a high extinction Glan laser calcite polarizer. The angle Θ between the polarizations of the aligning and the driving laser fields was adjusted by tuning a half-wave plate in the path of the aligning beam. An adjustable iris was placed along the path of the two beams to control and ensure the focus point of the aligning laser to be larger than that of the driving laser in the focusing region of the supersonic gas jet. The two laser pulses were collinearly focused into the gas zone by a lens (f = 300 mm). The intensity of the aligning laser was about and that of the driving laser was . The N₂ (99.999%) gas was introduced into the chamber with a diffuse nozzle ( diameter) with a backing pressure about 2 bar. The density of gas in the interaction region was about with a rotational temperature less than 100 K, which was estimated by the supersonic expansion of the molecular beam in the gas jet. The generated harmonics signals were reflected by an Au-coated mirror into the XUV spectrometer where the harmonics were spectrally resolved by a spherical grating with a groove density of 1200 groves/mm (Shimadzu 30–002) and then were imaged onto a microchannel plate detector (Tectra) fitted with a phosphor screen (P46). The signals from the phosphor screen were recorded by a CCD (Hamamatsu ORCA R2) with a high dynamic range. Each harmonic intensity was extracted by integrating the images in the spatial (vertical) and spectral (horizontal) directions. Each spectrum was typically averaged over laser shots.

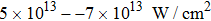
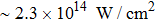
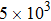
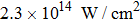
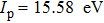
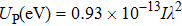
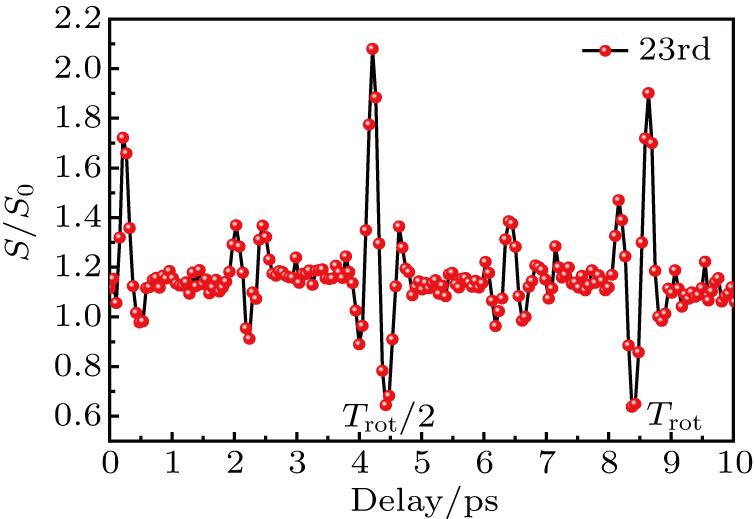
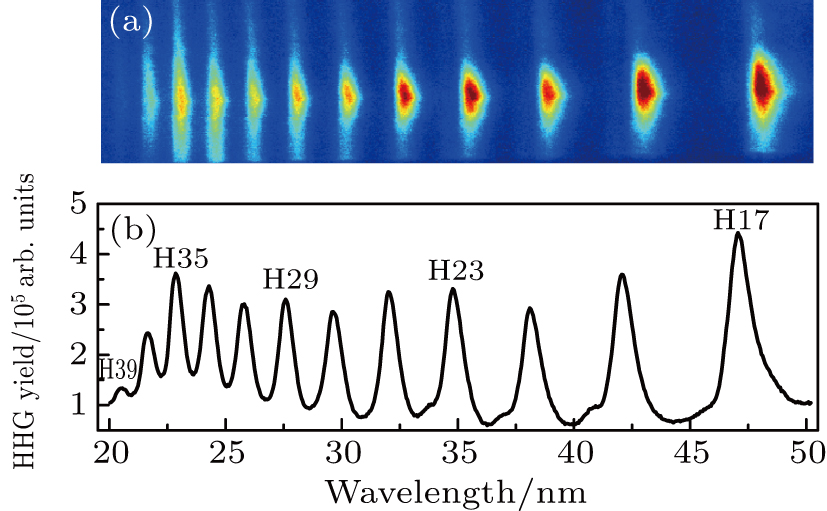We present part of harmonic spectrum of nitrogen (N₂) molecules irradiated by an 800 nm, 35 fs linearly polarized driving laser with peak intensity of in Fig. 1(a). The corresponding integrated HHG intensity is shown in Fig. 1(b). The orders of HHG are indicated in Fig. 1(b) as Hn (n is the order of the harmonics). For HHG in strong laser fields, the cutoff energy of HHG is expressed as^[9,35]

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (a) Part of harmonic spectrum of N2 generated by an 800 nm, 35 fs linearly polarized driving laser with peak intensity of 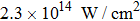, (b) the corresponding integrated HHG intensity.

We first measure the dependence of the harmonic intensity on the delay time between the aligning and driving lasers with linear polarization. The polarizations of the lasers are parallel to each other. Figure 2 shows the result of the 23rd harmonic as an example, in which the ratio of the harmonic intensity of the aligned molecules to that of the nonaligned molecules ( ) is presented. In our experiments, the pulse duration of the driving laser τ =35 fs is more than two orders of magnitude shorter than the rotational period of N₂ molecules ( ps). Thus the aligning pulse will induce a nonadiabatic field-free alignment. The interaction firstly excites a rotational wave packet.^[36–38] During the field-free evolution, the created molecular rotational wave packet rephrases when the pulse has passed, aligning the molecules periodically along the polarization direction of the laser. The effect of such nonadiabatic impulsive alignment on the molecules results in the modulation in the intensity of the harmonics upon changing the delay time between the aligning and driving laser fields.^[16,17] As shown in Fig. 2, the deepest modulation occurs at a delay time of T_rot/2 (half revival) or T_rot (full revival), corresponding to revivals of the aligned state. In the following measurements, the delay time is set at 4.1 ps, corresponding to a half-revival when the molecular axis is aligned parallel to the polarization of the aligning laser field.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Experimental result of the 23rd order harmonic depending on the delay time between the aligning and driving lasers with parallel polarization. Ratio of harmonic yield of the aligned molecules S to that of the nonaligned samples S0 is shown. The first half revival Trot/2 and full revival Trot are marked in the figure.

We then investigate the angular dependence of HHG by adjusting the polarization direction of the linearly polarized aligning laser with respect to that of the driving laser. Figure 3 shows the polar plots of the angular distributions of the plateau harmonics (H25 and H33, Figs. 3(a) and 3(b)) and those for the cutoff harmonics (H37 and H39, Figs. 3(c) and 3(d)). Quite different behaviors in the angular distributions of the plateau and cutoff harmonics can be observed. For the plateau harmonics, the angular distribution has a maximum at parallel polarization (Θ=0° or 180°) and the harmonic signal is greatly suppressed for the polarization of the driving laser being perpendicular to that of the aligning laser (Θ=90° or 270°) (see Figs. 3(a) and 3(b)). However, the angular distributions of the cutoff harmonics show a relatively complex feature. A dip appears at parallel polarization, and the signal turns to increase with perpendicular polarization, leading to a small peak as shown in Figs. 3(c) and 3(d).

Fig. 3.

	Figure Option ViewDownloadNew Window
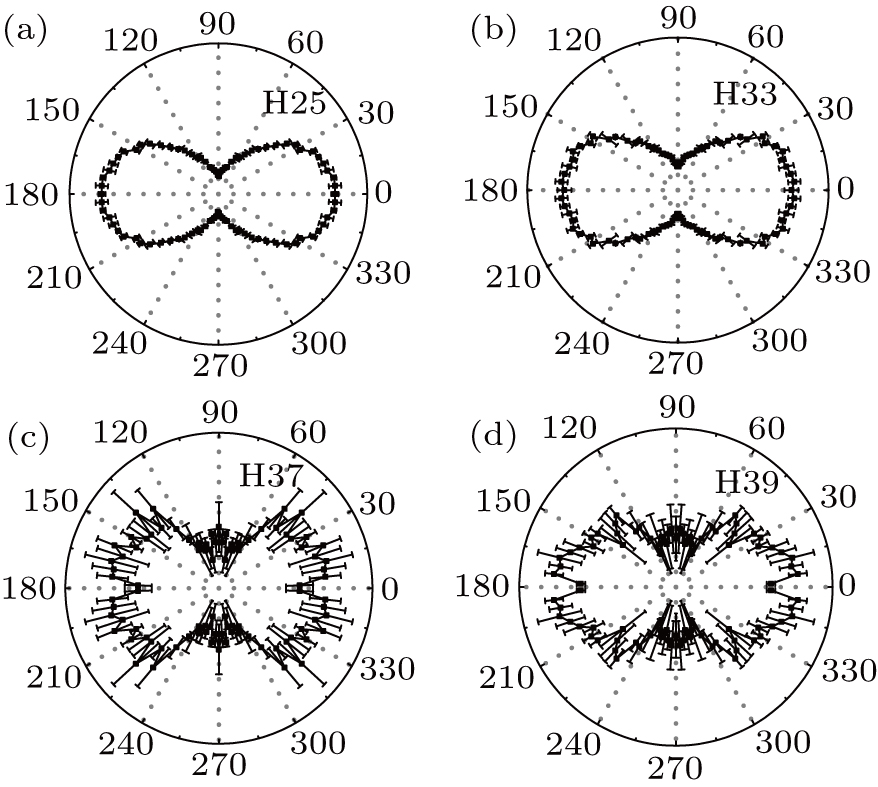	Fig. 3. Angle-dependence of the harmonic yield for (a) H25, (b) H33, (c) H37, and (d) H39. Ratio of harmonic yield of the aligned molecules to that of the nonaligned molecules is presented.

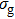
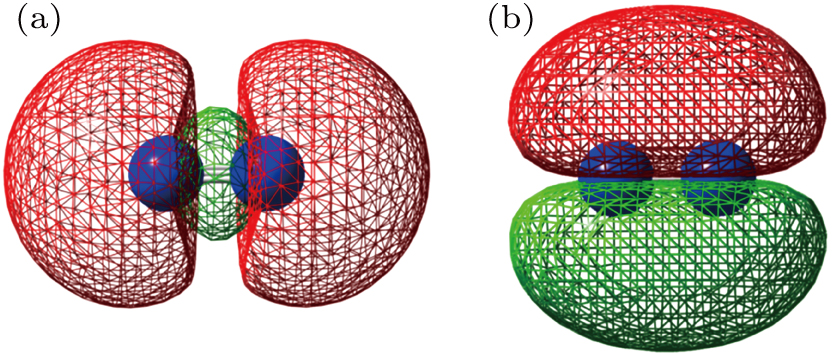It is well known that molecular HHG in strong laser fields is governed by the symmetry of the molecular orbitals and the electronic structures. In other words, the harmonic yield would reflect the information of the molecular orbitals. The HOMO of N₂ is a orbital with a nodal plane perpendicular to the molecular axis (see Fig. 4(a)). Thus, the electronic ionization probability reaches a maximum along the molecular axis (Θ=0°). If N₂ is aligned perpendicular to the driving laser (Θ=90°), the electronic ionization from HOMO will be highly suppressed owing to the nodal plane of the orbital. Generally speaking, HHG is usually understood as tunneling ionization from HOMO and returning to the tunnel exit for recombination. Thus, the dependence of the ionization probability of the HOMO electron on the alignment angle leads to similar angular distributions of HHG as we have shown in Figs. 3(a) and 3(b).

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Structures of (a) HOMO and (b) HOMO-1 of N2 calculated at B3LYP/6-311++G**level with Gaussian 03[39] program and plotted with Multiwfn package.[40]

On the other hand, the peculiar angular distributions for the cutoff harmonics shown in Figs. 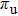3(c) and 3(d) strongly indicate the contributions of the lower-lying molecular orbitals to the HHG. The electron density distribution of HOMO-1 of N₂ is perpendicular to the molecular axis (see Fig. 4(b)), implying that HHG from HOMO-1 would be predominant at the perpendicular alignment. The contribution of HOMO-1 to the HHG leads to additional distributions when the polarization of the driving laser is perpendicular to that of the aligning laser (Θ=90° or 270°), as shown in Figs. 3(c) and 3(d). Our results indicate that the effect of HOMO-1 on HHG of N₂ is more significant in the cutoff region than that in the plateau region, which has also been observed in previous studies.^[28,29,31]

In order to further explore the multi-orbital effect of HHG from aligned N₂ molecules, we investigate the ellipticity dependence of HHG. Figure 5 shows the ellipticity dependence of H21, H27, H31, H37, and H39 of the aligned N₂ molecules with parallel (Fig. 5(a)) or perpendicular (Fig. 5(b)) polarization. It can be seen that the harmonic signal decreases rapidly with increasing ellipticity of the driving laser. This can be well understood in the frame of the three-step rescattering scenario, since the recombination of the tunneling electron with the parent ion will diminish because of the drift momentum spread of the returning electronic wavepacket in an elliptically polarized laser.^[9]

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Normalized harmonic intensity as a function of ellipticity of H21 (black squares), H27 (red circles), H31 (blue triangles), H37 (pink inverted triangles), and H39 (green diamonds) from N2 molecules aligned (a) parallel and (b) perpendicular to the major axis of the elliptical polarization plane. Peak intensity of the 800 nm driving laser is .

One may notice from Fig. 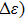5 that the ellipticity dependence is different for different order harmonics as well as for different alignments. To further elucidate this, we present in Fig. 6 the full width half maximum (FWHM, by fitting each curve in Fig. 5 with a Gaussian function. For either of the alignments, apparent increment of FWHM is observed for higher order harmonics comparing to that of the lower order harmonics, indicating the weaker dependence on the laser ellipticity. Another observation is that for each order of harmonics, the width measured with perpendicular alignment is larger than that with parallel alignment. As we have mentioned above, the angular distribution shown in Fig. 3 indicates that both HOMO and HOMO-1 contribute to the HHG of N₂ molecules and the effect of HOMO-1 is more significant for the cutoff harmonics with perpendicular alignment. Thus, the results in Figs. 5 and 6 strongly indicate that HHG from HOMO-1 exhibits a weaker ellipticity dependence comparing to that from HOMO of N₂ molecules.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Full width half maximum by fitting each curve in Fig. 5 with a Gaussian function for the parallel (red triangles) and perpendicular (blue squares) configurations.

According to the simple-man model, the ellipticity dependence should be stronger for an atom with a higher ionization potential (I_p).^[41] This is opposite to the present results of N₂, as I_P of HOMO-1 (16.96 eV) is higher than that of HOMO (15.58 eV). It is expected that the structure of different molecular orbitals should play a significant role that results in different ellipticity dependence of the harmonics. The electron in the 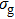HOMO is more localized than that in the HOMO-1 of N₂. This would imply that the electron wavepacket of tunneling ionization from HOMO-1 could be more diverse than that from HOMO, leading to a broader distribution of the transverse velocity of the tunneling electron that should be canceled out by the drift velocity caused by the elliptically polarized laser field. As a result, the ellipticity dependence would be weaker as we have observed in the study. Our results should stimulate further experimental and theoretical investigations on the effect of molecular orbitals on various physical processes induced by strong laser fields.

In summary, we have investigated the effects of multiple orbitals to the HHG from aligned N₂ molecules in both linearly and elliptically polarized strong laser fields. The measured angular dependence of HHG from aligned N₂ molecules in the plateau and cutoff regions indicates the contribution from both HOMO and HOMO-1. By measuring the ellipticity dependence of different harmonic orders and different alignments, we discuss the effect of the structures of the molecular orbitals on HHG of N₂ molecules. Our study indicates that the investigation on the aligned molecules with both linearly and elliptically polarized strong laser fields would open a route to investigate the multi-orbital effects on molecular HHG.