Cite this Article
Gao Ying-Hao, Li Yuan-Ji, Feng Jin-Xia, Zhang Kuan-Shou. Stable continuous-wave single-frequency intracavity frequency-doubled laser with intensity noise suppressed in audio frequency region. Chinese Physics B, 2019, 28(9): 094204  
Permissions
Stable continuous-wave single-frequency intracavity frequency-doubled laser with intensity noise suppressed in audio frequency region
Gao Ying-Hao1, Li Yuan-Ji1, 2, †, Feng Jin-Xia1, 2, Zhang Kuan-Shou1, 2
State Key Laboratory of Quantum Optics and Quantum Optics Devices, Institute of Opto-Electronics, Shanxi University, Taiyuan 030006, China
Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China

 

† Corresponding author. E-mail: liyuanji@sxu.edu.cn

Abstract
Abstract

We demonstrated a continuous wave (cw) single-frequency intracavity frequency-doubled Nd:YVO4/LBO laser with 532 nm output of 7.5 W and output of 3.1 W, and low intensity noise in audio frequency region. To suppress the intensity noise of the high power 532 nm laser, a laser frequency locking system and a feedback loop based on a Mach–Zehnder interferometer were designed and used. The influences of the frequency stabilization and the crucial parameters of the MZI, such as the power splitting ratio of the beam splitters and the locking state of the MZI, on the intensity noise of the 532 nm laser were investigated in detail. After the experimental optimizations, the laser intensity noise in the frequency region from 0.4 kHz to 10 kHz was significantly suppressed.

PACS: 42.55.Xi;42.65.Ky;42.50.Lc
Keyword:continuous wave single-frequency intracavity frequency-doubled laser;noise suppression;power stabilization;audio frequency
1. Introduction

Continuous-wave (cw) single-frequency all-solid-state lasers with the features of low noise, good beam quality, and long coherent length have found applications in a number of fields, including quantum information, cold atom physics, and precise measurements.[1–9] In particular, a single-frequency laser source with high power dual-wavelength output is more beneficial to those investigations and measurements. 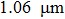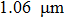For example, in the generations of squeezed states and entanglements at , the pump filed, the local oscillator, the signal field for the optical parametric amplifier (OPA) or optical parametric oscillator (OPO), and the auxiliary beams used for cavity locking and phase locking can be provided simultaneously by a multi-Watts level single-frequency and 532 nm dual-wavelength laser.[10] In precise distance measurements based on heterodyne laser interferometer, the dual-wavelength laser source can be used to compensate the measurement error originated from the instability of the refractive index of the ambient air, and the measurement uncertainty can thus be improved comparing with the single-wavelength laser based interferometer.[11] Moreover, single-frequency and 532 nm dual-wavelength lasers can also be used to generate the red-detuning[12] and blue-detuning[13] magneto-optical traps for cooling and trapping the atoms, respectively.

Although single frequency lasers with high power 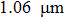and 532 nm dual-wavelength output have already been demonstrated by using the unidirectional traveling wave cavity technique and the intracavity second harmonic generation technique,[14,15] noise reduction techniques and effective power stabilization methods for the dual-wavelength laser sources are still waiting for a detailed study to meet the need of the generation of stable squeezed states and multi-partite entanglements in the audio frequency band, for the reason that the intensity noise and the power fluctuation of the laser source are directly coupled into the response of the photodetectors, and the level of squeezing or entanglement at low frequency is undulated and degraded.

Intensity noise reduction and power stabilization were generally investigated simultaneously in previous works. When a feedback loop based on a combination of an electro-optical amplitude modulator (EOAM) or acousto-optic modulator (AOM) and a polarized beam splitter (PBS) was employed to stabilize the laser power, the laser intensity noise could be suppressed at the same time.[16–18] Unfortunately, both commercially available and custom made EOAMs or AOMs may lead to a beam quality deterioration of the incident 532 nm laser and the maximum permitted power density of the incident 532 nm laser for an EOAM is generally 0.5 W/mm2. Apart from this method, the laser intensity noise can also be reduced by utilizing a mode cleaner (MC) acting as a low-pass filter,[19,20] but the noise reduction band of the method using MC is restricted by the bandwidth of the MC. Unbalanced Mach–Zehnder interferometer (MZI) is a kind of device that can be used for laser noise suppressing in some discrete frequencies, but not in the audio-frequency region.[21,22] Consequently, some other method should be developed to build a laser source with low intensity noise in the Hz to kHz range and good power stability, which is of benefit to the generation of squeezed state in the audio-frequency region that can be used in the gravitational wave detection.

In this paper, we demonstrate a noise reduction and frequency stabilization system for an intracavity frequency-doubled laser with multi-Watts output. The configuration of the intracavity frequency-doubled laser to be optimized is simply described in section 2. In subsection 3.1, the laser frequency stabilization method based on controlling the linear and nonlinear losses of the laser, as well as employing a feedback loop based on a stable frequency reference is introduced. In subsection 3.2, a balanced MZI and the feedback loop are designed for reducing the intensity noise of the 532 nm laser in the audio-frequency region without degrading the laser beam quality. The influences of the frequency stabilization and the crucial parameters of the MZI, such as the power splitting ratio of the beam splitters and the locking state of the MZI, on the intensity noise of the 532 nm laser are investigated in detail.

2. Experimental setup

The experimental setup of the high power cw single-frequency intracavity frequency-doubled laser and stabilization system is shown in Fig. 1. The pump source is a commercially available laser diode (model: LIMO-A 1294, LIMO) with the center wavelength of 808 nm and a maximal output power of 60 W. Pump light passing through a fiber with core diameter of and a collimated lens (f1) is split into two beams with orthogonal polarizations by a polarized beam splitter (PBS1). The reflected pump beam and the transmitted pump beam whose polarization is rotated 90° by a half wave plate (HWP1) are both focused into the gain medium via two identical focusing lenses (f2). The gain medium is an a-cut Nd:YVO4 crystal with a cross-section of 3 mm × 3 mm × 20 mm and the Nd concentration of 0.2 at.%. Both end-faces of the Nd:YVO4 crystal are anti-reflection (AR) coated at 808 nm and ( and ). To suppress the oscillation of the σ-polarization mode and eliminate the etalon effect, a wedge shape of 1.5° is cut on one end-face of the crystal with respect to the c-axis of the crystal. For longitudinal mode selection, a ring resonator composed of 6 mirrors (M1–M6) and an optical diode formed by a HWP2 and a Faraday rotator based on a terbium gallium garnet (TGG) are employed. The four plane mirrors (M1, M2, M3, M6) are high reflection (HR) coated at and high transmission (HT) coated at 808 nm (45°, , and ). M4 and M5 are concave mirrors with curvature radii of 100 mm, where M4 is HR coated at ( ) and fixed onto a pizeoelectric-transducer (PZT1) to control the cavity length, M5 acting as the output coupler is partially transmission coated at . A type-I noncritical phase-matched LBO crystal with dimensions of 3 mm × 3 mm × 18 mm is chosen for intracavity frequency doubling because of its high damage threshold and large temperature and angular acceptances. The lithium triborate (LBO) crystal with two end-faces AR coated at and 532 nm ( %) is inserted into the ring cavity at the center of the M4–M5 arm. Both the Nd:YVO4 and LBO crystals are tightly wrapped with indium for reliable heat transfer and mounted in copper ovens that are temperature controlled using a home-made temperature controller with an accuracy of 0.01 °C. The whole cavity length is 490 mm.

Fig. 1. Experimental setup of high power cw single-frequency dual-wavelength laser and stabilization system. LPF: low pass filter; M: mixer; HV: high voltage amplifier; AMP: power amplifier; dc: direct current source; OI: optical isolator; EOM: electro-optic modulator; PID: proportional-integral-derivative amplifier; A and B: negative power combiner; +/−: positive/negative power combiner; SA: spectrum analyzer.

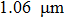
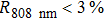
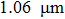
The outputs of fundamental and second harmonic lasers are isolated from the laser resonator using two optical isolators (OIs) and separated using a dichroic mirror (DBS). The laser is split into three parts using HWP3, HWP4, PBS2, and PBS3. One portion is sent to a power meter (PM1, model: LabMax-Top, Coherent). The other two beams are delivered to a scanning Fabry–Pérot (F–P1) interferometer (free spectral range: 375 MHz; finesse: 350) for monitoring the longitudinal-mode and to a frequency stabilization system for stabilizing the frequency of the laser, respectively. The 532 nm laser is injected into the power stabilization system based on a MZI to reduce its power fluctuation and intensity noise. The long-term power fluctuation and the intensity noise of the stabilized laser are record using PM2 and a balanced detection (BD) system formed by HWP8, PBS5, and a pair of low noise, broadband detectors (PD4 and PD5), respectively. The common-mode rejection ratio of the BD system is higher than 40 dB. The sum and difference of the detected ac signals are recorded by a spectrum analyzer (SA, model: N9030 A, Agilent). The sum signal gives the intensity noise power of the laser and the difference signal gives the shot noise limit (SNL).

3. Experimental results and discussion
3.1. Mode-hop-free and frequency stabilized laser operation

Based on our previous work on the modeling of the sufficient condition of stable single frequency laser operation with energy transfer upconversion and excited stimulated absorption taken into account,[23] and considering the power requirement for building the multi-partite entanglements and squeezed states, an output coupler (M5 in the laser cavity) with a transmission of 1.3% at 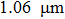and a transmission higher than 99.5% at 532 nm, as well as an LBO temperature of 149.2 °C, which leads to a nonlinear conversion coefficient of 1.346 × 10−10 m2/W that is far beyond the critical value of 0.373 × 10−11 m2/W, were chosen for the generation of the dual-wavelength laser. Figure 2 shows the measured input–output behavior of the laser and the longitudinal mode spectrum. The results indicate that the 532 nm and outputs as high as 9.5 W and 3.1 W are achieved simultaneously under 50 W pumping, and there is only one longitudinal mode oscillated stably with no mode hop. The beam quality of the dual wavelength lasers was also measured using a laser beam quality analyzer (model: M2-200-BB; CCD: GRAS-20S4M-C, Spricon), the beam quality factors of the laser were and . The beam quality factors of the 532 nm laser were and . The beam spot radius of the 532 nm laser 0.3 m apart from the cavity was about , the near-field divergence angle of the 532 nm laser was 5.9 mrad.

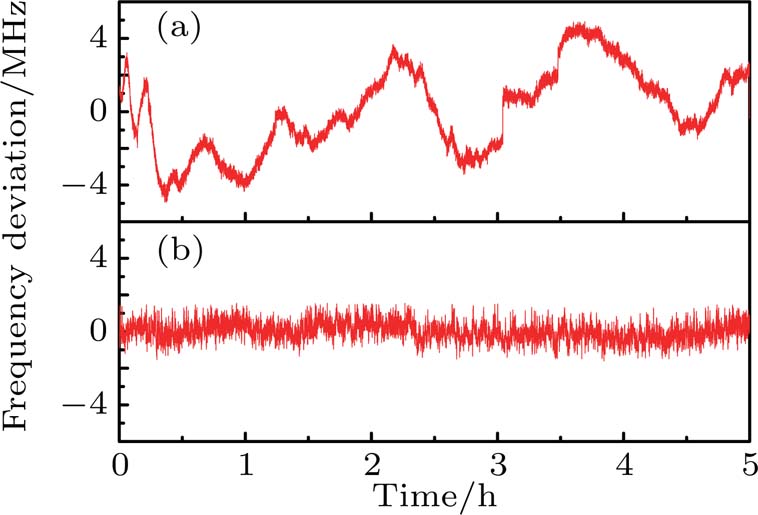
Fig. 2. Output powers of and 532 nm lasers versus incident pump power. Inset: transmitted intensity of F–P1 interferometer.

By using a digital oscilloscope (model: DPO7245, Tektronix) and a software based on Labview, the laser frequency deviation from the initial frequency as a function of time was measured and shown in Fig. 33(a). It can be seen that the peak to peak frequency drift of the free running laser during 5 h was about ± 4.8 MHz with no mode hop observed. To further stabilize the laser frequency, a 200 mm-long confocal F–P2 cavity, which was consisted with a tube-shaped invar body and two concave end mirrors with curvature radii of 200 mm, was built as a frequency standard. The finesse of the cavity was measured to be 1000, leading to a linewidth of 375 kHz. Since a temperature fluctuation of the invar body as low as 0.1 °C will cause the resonant frequency to drift within 20 MHz, an active temperature control system was designed and employed to maintain the length of the F–P2 cavity. The invar tube body was embedded in a copper sheath with an exterior contour of cuboid, whose four side faces were in close contact with eight pieces of thermoelectric cooler (TEC) modules (40 mm × 20 mm), and covered by an intermediate polyarylsulfone thermal insulation layer and an outermost aluminum shell acting as heat sink. With the help of a homemade temperature controller, a long term temperature stability of ±0.003 °C during 5 h was achieved. Based on this robust frequency reference, Pound–Drever–Hall (PDH) frequency locking was demonstrated via a frequency stabilization loop (FSL) as shown in Fig. 1. The fundamental laser beam was firstly phase modulated by an electro-optic modulator (EOM) to generate frequency-modulated sidebands which were 80 MHz apart from the carrier. Then the laser reflected from the F–P2 cavity was detected by a photo-detector (PD2), and the detected signal was multiplied with the local oscillator’s signal using a mixer (M) with a phase compensation provided by a delay box. After being filtered by a low-pass filter (LPF), the error signal was obtained and sent to a proportional-integral-derivative (PID) amplifier and a high voltage amplifier (HV) to drive the laser PZT1. Figure 3(b) shows the frequency drifts of the stabilized laser during 5 h. Once FSL was working, the long term peak to peak frequency drift was less than ±1.5 MHz.

Fig. 3. Frequency drift of (a) free running laser and (b) stabilized laser in 5 h.
3.2. Intensity noise suppression and power stabilization

To stabilize the output power and suppress the intensity noise of the 532 nm laser, a MZI and the corresponding power stabilization loop (PSL) as shown in Fig. 1 were used. The MZI was composed of two HR coated mirrors M12, M13 and two beam splitters (BSs) M10, M11 with a beam splitting ratio of R at 532 nm. The mirror M12 was attached on a PZT3 for tuning the optical length difference (OPD) between the two arms of the MZI. Then the difference between an adjustable low noise direct current (dc) signal and the low frequency part (dc to 40 kHz) of the detected signal from PD5 was filtered by a LPF and sent to a PID and a HV to generate the driving signal, which was finally fed back to PZT3 for locking the OPD. When the voltage of the dc signal was adjusted and the parameters of the proportional-integral-derivative amplifier were tuned accordingly, the transmission of the stabilized laser passing through the MZI (Tlock) can be changed. To investigate the influence of the MZI parameters, e.g., Tlock and R, on the laser noise properties in the audio frequency region (0.4–30 kHz), the same settings were adopted during the following measurements: Firstly, the laser power incident on PD4 and PD5 was kept at . Secondly, the sectional measurements in four Fourier frequency windows including 0.4–0.8 kHz, 0.8–3.2 kHz, 3.2–10 kHz, and 10–30 kHz were carried out for each noise spectrum, and the resolution bandwidths (video bandwidths) of SA in the respective regions were set as 2 Hz (2 Hz), 4 Hz (4 Hz) 16 Hz (4 Hz), and 16 Hz (4 Hz). Thirdly, to reduce the measurement errors, each data point in Figs. 4 and 5 was the averaged value of the data recorded in 400, 400, 800, and 800 measurements for the four Fourier frequency windows. Fourthly, since the electronic noise was at least 10 dB below the SNL in the frequency region, it had already been subtracted from the measured data.

To investigate the influence of Tlock on the laser intensity noise property, the BSs with R = 50% were used to build the MZI, and the noise spectra were recorded when the OPD of the MZI was locked at different Tlock, as shown in Fig. 4. Curves (i) and (ii) are the SNL and intensity noise of the 532 nm laser before the MZI. It can be seen that in the audio frequency region from 0.4 kHz to 30 kHz, the intensity noise of the laser was always higher than the SNL with a difference ranging from 12 dB to 34 dB. Once the 532 nm laser was stabilized using the MZI and PSL, a noise transfer phenomenon was observed. Curves (iii), (iv), and (v) in Fig. 4 are the intensity noises in the laser output from the locked MZI when Tlock is 45%, 65%, and 85%, respectively. It can be seen that most of the intensity noise in the laser output from the MZI in the frequency region from 0.7 kHz to 10 kHz was suppressed in all the three cases, while the intensity noise in the frequency region from 10 kHz to 30 kHz was raised up beyond the intensity noise of laser before MZI. Moreover, the amount of noise suppression in the frequency region of 0.7–10 kHz can be adjusted by controlling the locking position of the MZI. As shown in Fig. 4, when Tlock was raised up from 45% to 85%, the intensity noise of the laser from 0.7 kHz to 10 kHz was closer to the SNL. In particular, in the analysis frequency region from 0.7 kHz to 3.7 kHz, the intensity noise of laser in the case of Tlock = 85% was more than 5 dB below that in the case of Tlock = 45%.

Fig. 4. Intensity noise of laser as a function of analysis frequency when R = 50%.

To test the influence of the beam splitting ratio on the intensity noise of the 532 nm laser, three MZIs with R = 90%, 75%, and 50% were used for 532 nm laser stabilization. Figure 5 shows the measured intensity noises of the laser before the MZI and the stabilized lasers output from the MZIs locked at the same Tlock of 85%. Curves (i) and (ii) are the SNL and intensity noise of the laser before the MZI. Curves (iii), (iv), and (v) are the intensity noises of the lasers output from the locked MZIs when R is 50%, 70%, and 90%, respectively. It can be seen that when the BSs with R = 90% were used to build the MZI, the intensity noise of the stabilized laser in the frequency region from 0.4 kHz to 3 kHz was further suppressed in comparison with the case of R = 50%, while the intensity noise of the stabilized laser in the frequency region from 3 kHz to 30 kHz became higher.

Fig. 5. Intensity noise of laser as a function of analysis frequency with different R of MZI at Tlock of 85%.

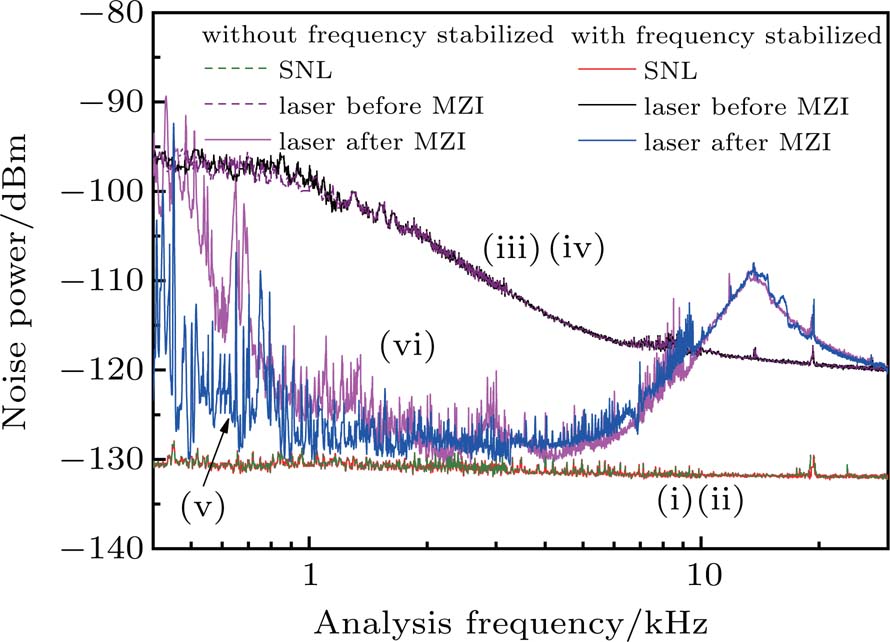The influence of laser frequency stabilization on the intensity noise suppression was also measured and shown in Fig. 6. Curves (i) and (ii) are the SNLs of the laser with and without laser frequency stabilization, respectively. Curves (iii) and (iv) are the intensity noises of the laser before the MZI with and without laser frequency stabilization, respectively. Curves (v) and (vi) are the intensity noises of the lasers output from the locked MZIs with and without laser frequency stabilization when R is 90% and Tlock is 85%, respectively. It can be seen that the laser frequency stabilization had nearly no influence on the measured SNL and the intensity noise of the laser before MZI. But the intensity noise of the laser after MZI showed significant suppression in the frequency region from 0.4 kHz to 1.3 kHz once the laser was frequency stabilized.

Fig. 6. Intensity noise of laser as a function of analysis frequency in the cases with or without laser frequency stabilization when R = 90% and Tlock=85%.

From the above experiment results, the best noise performance was achieved when the laser was frequency stabilized, the MZI with R = 90% was employed and locked to the state of Tlock = 85%. The performance of laser power stability at the same condition was also measured, as shown in Fig. 7. The measured peak to peak power fluctuation of the 532 nm laser before MZI was less than ±0.7% for a given 5 h. As a comparison, when the 532 nm laser was stabilized via an MZI, the 532 nm output power from the locked MZI was 7.5 W, and the measured peak to peak power fluctuation of laser was less than ±0.2% for a given 5 h.

Fig. 7. Power fluctuation of the 532 nm laser before MZI (0–5 h) and output from a locked MZI (5–10 h).
4. Conclusion and perspectives

We built up a high power mode-hop-free cw single-frequency intracavity frequency-doubled Nd:YVO4/LBO laser, the output power and intensity noise in the audio frequency region of 532 nm laser were stabilized and suppressed via a locked MZI. By utilizing the resonant frequency of a temperature controlled confocal F–P cavity as frequency standard, the frequencies of the dual-wavelength laser were locked via PDH technique, and the measured frequency drift of the laser was better than ±1.5 MHz for a given 5 h. Furthermore, a control system based on MZI was designed and used to improve the power stability and the intensity noise property of the 532 nm laser. When the control system was working, the measured power fluctuation was less than ±0.2% during a given 5 h, and the intensity noise was significantly suppressed in the audio frequency region by optimizing the locking level and the beam splitting ratio. Finally, a robust cw single frequency laser operation with 532 nm output of 7.5 W and output of 3.1 W was achieved. The stable low noise high power cw single-frequency intracavity frequency-doubled laser can satisfy the experimental requirements for the generation of audio frequency band squeezed state and multi-partite entanglement. The laser can also be applied in the fields of quantum information and precise measurements.

Reference
[1] Kómár P Kessler E M Bishof M Jiang L Sørensen A S Ye J Lukin M D 2014 Nat. Phys. 10 582 https://doi.org/10.1038/nphys3000
[2] Shuman E S Barry J F DeMille D 2010 Nature 467 820 https://doi.org/10.1038/nature09443
[3] Liu L W Gengzang D J An X J Wang P Y 2018 Chin. Phys. B 27 034205 https://doi.org/10.1088/1674-1056/27/3/034205
[4] Goda K Miyakawa O Mikhailov E E Saraf S Adhikari R McKenzie K Ward R Vass S Weinstein A J Mavalvala N 2008 Nat. Phys. 4 472 https://doi.org/10.1038/nphys920
[5] Fan H Y Xu X X Hu L Y 2009 Chin. Phys. B 18 5139 https://doi.org/10.1088/1674-1056/18/12/007
[6] Shao B Xiang S H Song K H 2009 Chin. Phys. B 18 0418 https://doi.org/10.1088/1674-1056/18/2/007
[7] Wu Q Xiao Y Zhang Z M 2015 Chin. Phys. B 24 104208 https://doi.org/10.1088/1674-1056/24/10/104208
[8] Feng J X Li Y J Zhang K S 2018 Chin. Phys. B 27 074211 https://doi.org/10.1088/1674-1056/27/7/074211
[9] Zhang Y C Fan L Wei C F Gu X M Ren S X 2018 Acta Phys. Sin. 67 024206 (in Chinese) https://dx.doi.org/10.7498/aps.67.20171848
[10] Vahlbruch H Mehmet M Danzmann K Schnabel R 2016 Phys. Rev. Lett. 117 110801 https://doi.org/10.1103/PhysRevLett.117.110801
[11] Meiners-Hagen K Meyer T Mildner J Pollinger F 2017 Appl. Phys. Lett. 111 191104 https://doi.org/10.1063/1.5000569
[12] Kuhr S Alt W Schrader D 2001 Science 293 278 https://doi.org/10.1126/science.1062725
[13] Nikolov A N Eyler E E Wang X T Li J Wang H Stwalley W C Gould P L 1999 Phys. Rev. Lett. 82 703 https://doi.org/10.1103/PhysRevLett.82.703
[14] Jin P X Lu H D Su J Peng K C 2016 Appl. Opt. 55 3478 https://doi.org/10.1364/AO.55.003478
[15] Zhang C W Lu H D Yin Q W Su J 2014 Appl. Opt. 53 6371 https://doi.org/10.1364/AO.53.006371
[16] Tricot F Phung D H Lours M Guérandel S Clercq E 2018 Rev. Sci. Instrum. 89 113112 https://doi.org/10.1063/1.5046852
[17] Junker J Oppermann P Willke B 2017 Opt. Lett. 42 755 https://doi.org/10.1364/OL.42.000755
[18] Kwee P Willke B Danzmann K 2011 Opt. Lett. 36 3563 https://doi.org/10.1364/OL.36.003563
[19] Shi Z Su X L 2010 Acta Sin. Quantum Opt. 16 158 (in Chinese)
[20] Liu Q Feng J X Li H Jiao Y C Zhang K S 2012 Chin. Phys. B 21 104204 https://doi.org/10.1088/1674-1056/21/10/104204
[21] Inoue S Yamamoto Y 1997 Opt. Lett. 22 328 https://doi.org/10.1364/OL.22.000328
[22] Zhang X Y Li Z Y Li Y M 2015 Acta Photon. Sin. 44 0827001 https://doi.org/10.3788/gzxb20154408.0827001
[23] Ma Y Y Li Y J Feng J X Zhang K S 2018 Opt. Express 26 1538 https://doi.org/10.1364/OE.26.001538