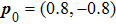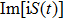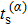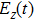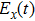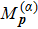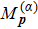† Corresponding author. E-mail:
Bichromatic circularly polarized fields provide a useful tool to probe the ionization dynamics. In this work, we compare the photoelectron momentum distribution in few-cycle bichromatic field of different helicities. The spectral features are analyzed with semiclassical trajectories derived from the strong field approximation. In particular, the interference fringes in momentum distribution are investigated by tracking the ionization time and tunneling exits of released photoelectrons. Different types of trajectories that contribute to the interference fringes are elucidated.
Over the last decades, the advent of the free electron laser and strong table-based lasers has propelled both time-resolved spectroscopic and structural investigations of matter in many aspects.[1,2] As one among various strong field phenomena, the ionization process in bichromatic circularly polarized laser fields has recently sparked much interest. The interplay between two pulses results in complicated photoelectron dynamics, and yields intriguing strong field phenomena, e.g., helical vortex structures[3] and symmetrical patterns[4] in photoelectron momentum distributions. Especially, concerning the relative helicity of the two pulses (co-rotating and counter-rotating fields), the distinct distributions of lobes in photoelectron momentum distribution confirm the possibility to control the ionization dynamics by helicities.[4] Switching between the counter-rotating and co-rotating fields, the ionization path via excited states can be altered to dramatically change the ionization rate.[5] The photoelectron can be steered by the relative helicity to rescatter with its parent ion,[6] or to circumvent the recollision and smoothly escape the core. It has been shown that the double ionization may occur in counter-rotating fields which are delicately tuned to drive the photoelectron back to its parent ion,[7,8] opening possibilities for probing electronic and molecular structure by adjusting impact angles of complex trajectories of the rescattering electron.[9] Meanwhile, the counter-rotating fields introduce the momentum-dependent spin asymmetry of photoelectrons, suggesting the potential applications of spin-polarized electron in attoscience.[10] Also, the bicircular fields provide the access to new mechanism of radiation in strong fields. The recollision induced by counter-rotating fields has inspired the new approach to high-order harmonic generation (HHG),[11] allowing for the generation of circularly polarized soft x-ray pulses.[12,13] On the other hand, it is reported that the efficiency of terahertz (THz) emission in co-rotating circularly polarized laser fields is five times higher than that with linearly polarized two-color femtosecond pulses.[14] The significant enhancement of THz radiation utilizing the simple experimental setup undoubtedly broadens the application scenarios of intense THz light source.
Comparing to a linearly polarized field, the circularly polarized field extends the dimension of the driving force, by which the photoelectron can be maneuvered with the extra degree of freedom. The richer information may help unravel the structure and dynamics that could not be resolved before. For instance, the electronic structure and rotational symmetry in molecules can be traced out by photoelectron driven by the bichromatic fields.[15–17] In addition, using a circularly polarized femtosecond laser pulse, the technique of attosecond angular streaking, i.e., attoclock,[18,19] can transform the rotation of the field polarization, which plays the role of the clock pointer, to the attosecond time resolution. Similarly, when bichromatic fields are present, a double-pointer attoclock can be designed by co-rotating field.[20] The photoelectron interferometer constituted by the two pointers allows probing the phase and the amplitude of photoelectron wave packets. Comparing the photoelectron distributions under counter- and co-rotating fields, the nonadiabatic offset of initial momentum distribution can also be easily assessed.[21] The attoclock using counter-rotating fields, on the other hand, allows for the clean investigation into the ionization steps in quasilinear polarization by inquiring the shift in the momentum distribution in the direction perpendicular to the momentum where the distribution peaks.[22] More subtle interference effects have also been studied. From the three-dimensional momentum distribution, the intra-cycle interference are observed by extracting from the momentum distribution along the light propagation direction.[23] The intensity-dependent interference structures have been observed, analogous to the spatially rotating temporal double-slit experiment with the variable slit width.[24] The interference can be dramatically affected by the Coulomb attraction of the parent ion or molecule since different paths of the electron wave packets are affected differently by the ionic potential.
In theory, the strong field approximation (SFA)[25–27] was widely used to investigate nonperturbative strong field physics. Based on the SFA, the interpretation in terms of electron trajectory derived from semiclassical approximation provides an intuitive understandings of various strong field processes, e.g., the well-known three-step model which explains the mechanism of the HHG. Especially since distinct types of trajectories are associated to different ionization pathways, semiclassical trajectories has been used to characterize the time delays of these pathways.[28,29] In addition, the concept of semiclassical trajectories provides a baseplate to incorporate effects that were not necessarily within the framework of the SFA, such as the long-range Coulomb interactions using trajectory-based Coulomb-corrected SFA[30–32] and analytical R-matrix theory.[33,34] The trajectories can also be easily evaluated in parallel, providing an efficient numerical method to investigate strong field dynamics. In this work, the method of the semiclassical trajectory has been extended to study the ionization dynamics in bichromatic circularly polarized fields. The selection of saddle points in circularly polarized fields is shown to be different from that in a linearly polarized field. Extra conditions are required to filter the solutions of saddle point equation. Utilizing the saddle points from the modified selection scheme, the initial conditions of trajectory calculation can be determined, and the procedure of further numerical calculation is the same as in a linearly polarized field.[31] Similar to the study in Ref. [35], we evaluate the photoelectron momentum distribution in a bichromatic circularly polarized fields, including a pulse of fundamental frequency (800 nm) and one of fifth-order frequency (160 nm). We focus on the formation of lobes and interference fringes under the few-cycle bichromatic circularly polarized fields in this work, presenting the comparison of spectral features between co-rotating and counter-rotating fields with trajectory analysis.
When an atom is subject to strong laser fields, nonperturbative ionization processes occur. The transition amplitude of the “direct” photoelectron with asymptotic momentum 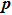
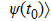
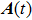
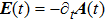
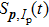
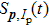

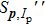
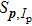

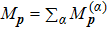
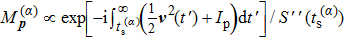
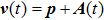
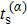

Note that 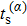
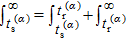
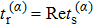
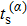
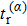

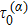
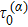
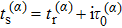
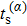
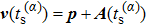
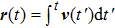
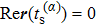

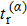
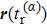
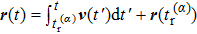
The numerical implementation of the trajectory-based calculation starts with the sampling of the asymptotic momentum 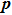
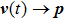
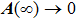
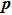

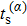
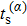
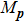
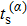
We emphasize that not all roots of Eq. (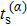
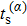

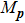
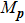

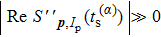
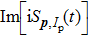
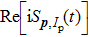

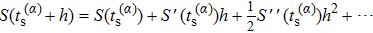
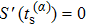
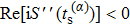
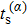
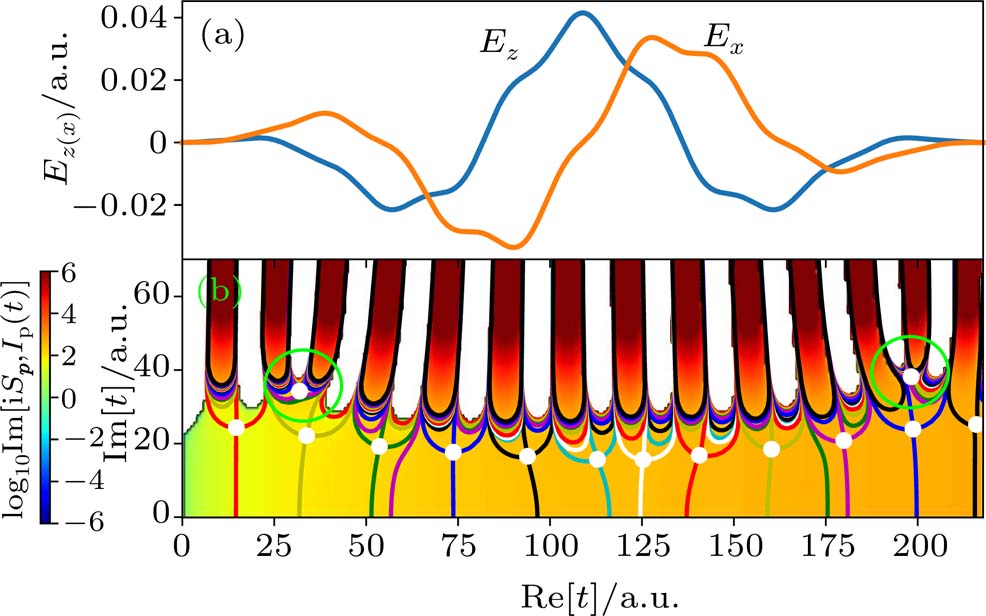
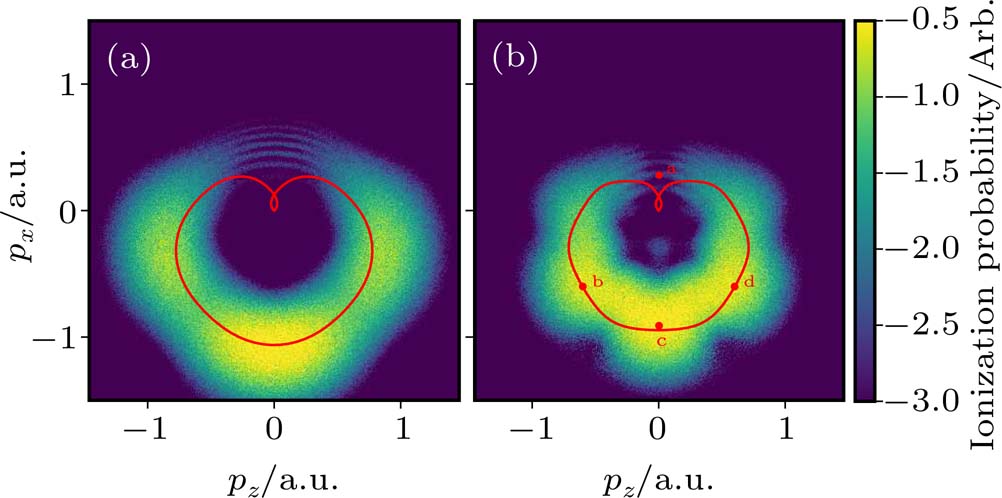
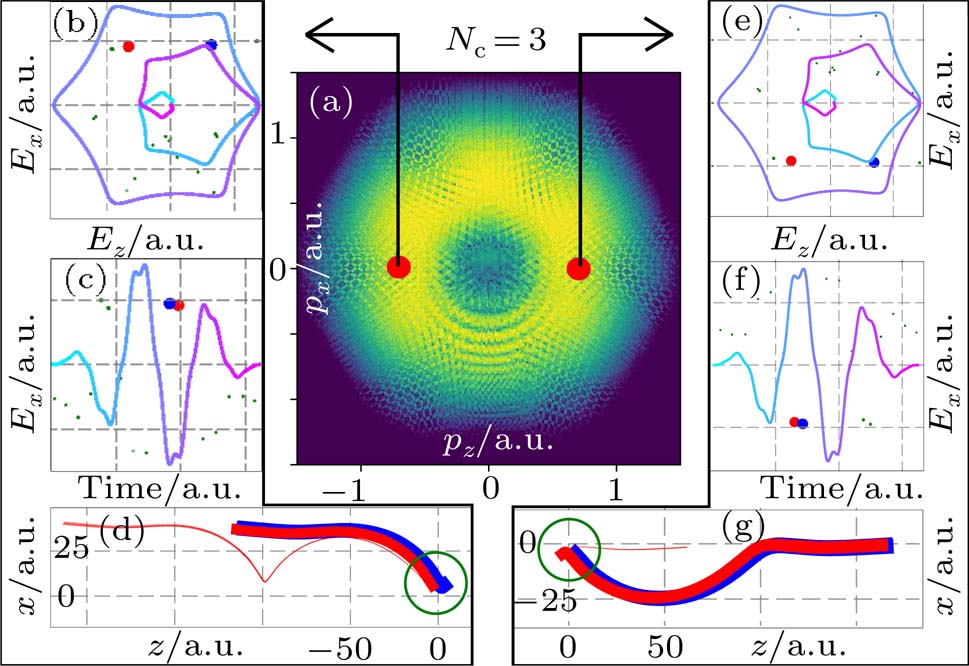
Under the bicircular laser fields, the momentum distributions for both co-rotating and counter-rotating field are investigated with trajectory analysis. The components of bicircular laser fields are given by
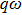
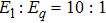
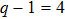
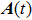
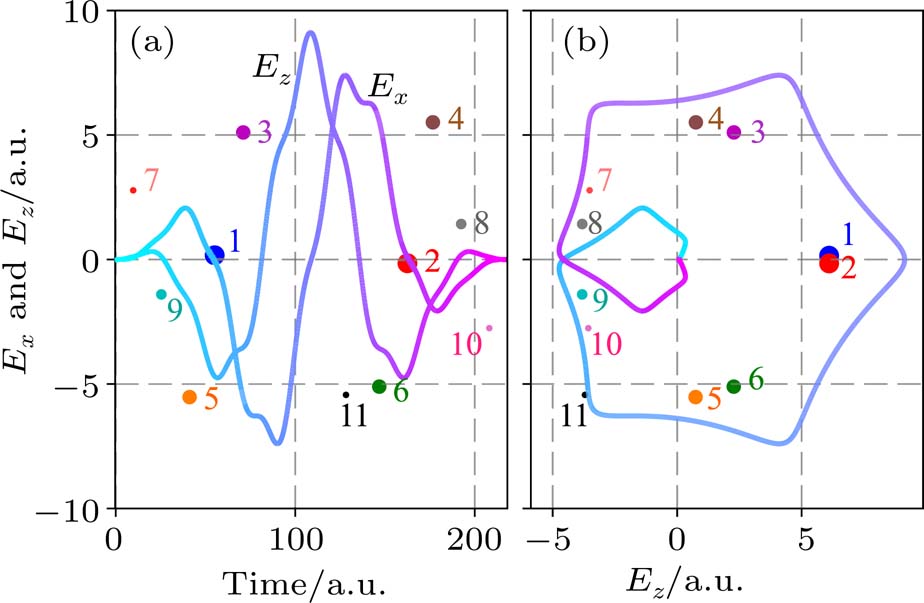
Taking sample point “a” for instance, all trajectories of the asymptotic momentum around “a” are selected. The temporal distribution of their tunneling time 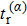
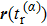
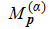
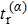
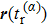
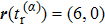
Starting with 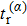
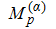
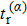
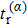
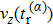
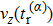
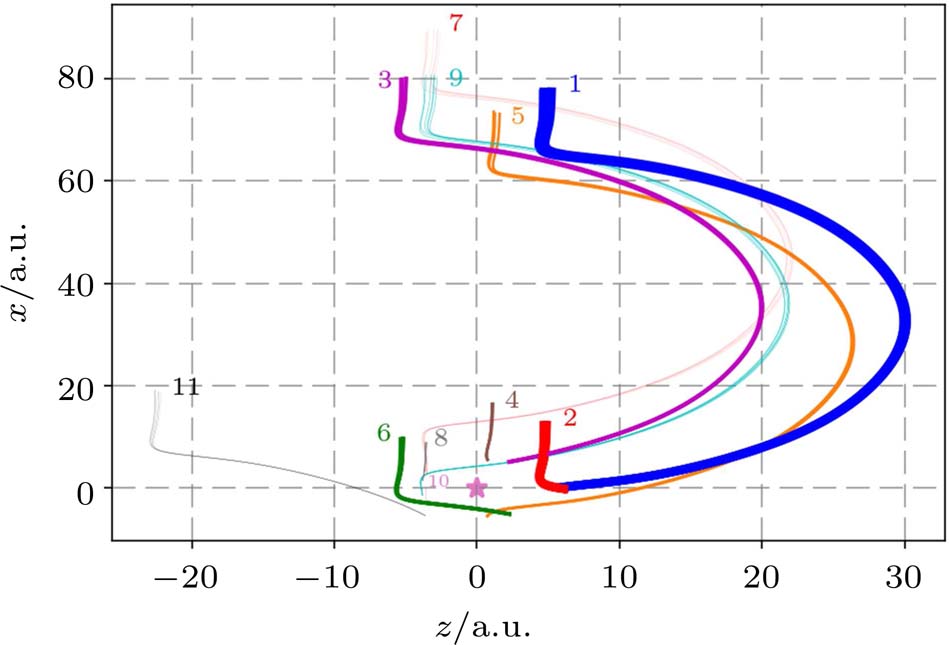 | Fig. 4. Photoelectron trajectories in counter-rotating fields starting with the initial time 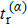
|
From the spatial distribution of 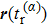
The above analysis focuses on point “a” in Fig.
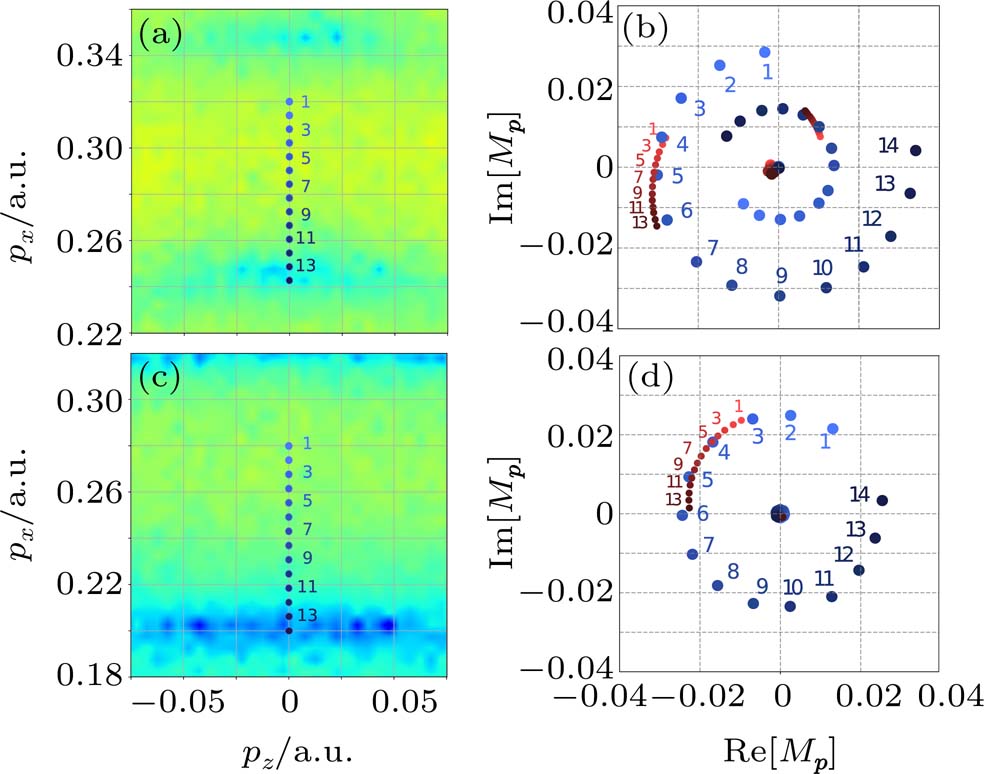
In Figs. 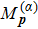
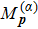

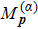
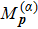
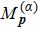
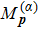
The formation of interference patterns is also studied by increasing Nc of the few-cycle laser fields. In Fig. 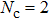
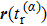
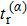
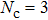
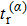
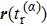
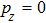
We have extended the semiclassical trajectory analysis to study the photoelectron momentum distribution in few-cycle bichromatic circularly polarized fields. When applying the method of the semiclassical trajectory, unlike the selection rule of saddle points for a linearly polarized field, in general, the solutions to the saddle point equation have to be filtered by imposing extra conditions. Evaluating the photoelectron momentum distributions with semi-classical trajectories, the work focuses on the comparison of lobes and interference patterns under the few-cycle co-rotating and counter-rotating fields. In this work, the field of fundamental frequency is assumed to be stronger than the field of qth order harmonic frequency. The photoelectron momentum distributions present different patterns of lobes and modulated interference fringes. The spectral features can be explored via tracking trajectories that contribute to the asymptotic momentum of interest. Especially under the few-cycle laser fields, the formation of interference can be elucidated by pinpointing all interfering trajectories. When the ionization probabilities of interfering trajectories are comparable, interference fringes become significant. The fringes along pz-axis for Nc = 3 originate from the interference between a pair of trajectories from within the same cycle, similar to the intra-cycle interference in a linearly polarized field. More intriguingly, the interference fringes along px-axis are already present when Nc = 2, which do not have the counterpart in a linearly polarized field. These fringes are shown to be caused by interference between trajectories of almost the same tunneling exits but from different cycles. Using bichromatic fields, it leaves open the possibility to investigate dynamics of photoelectron from given tunneling exits, e.g., the sub-barrier propagation accumulated phase during the tunneling process,[37,38] via the phase information encoded in the interference structure.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] |