Cite this Article
Chen Xia, Yin Li-Yuan, Liu Yong-Tai, Liu Hao. Hybrid-triggered consensus for multi-agent systems with time-delays, uncertain switching topologies, and stochastic cyber-attacks. Chinese Physics B, 2019, 28(9): 090701  
Permissions
Hybrid-triggered consensus for multi-agent systems with time-delays, uncertain switching topologies, and stochastic cyber-attacks
Chen Xia, Yin Li-Yuan †, Liu Yong-Tai, Liu Hao
School of Automation, Shenyang Aerospace University, Shenyang 110136, China

 

† Corresponding author. E-mail: 2992868494@qq.com

Abstract

We propose a new approach to discuss the consensus problem of multi-agent systems with time-varying delayed control inputs, switching topologies, and stochastic cyber-attacks under hybrid-triggered mechanism. A Bernoulli variable is used to describe the hybrid-triggered scheme, which is introduced to alleviate the burden of the network. The mathematical model of the closed-loop control system is established by taking the influences of time-varying delayed control inputs, switching topologies, and stochastic cyber-attacks into account under the hybrid-triggered scheme. A theorem as the main result is given to make the system consistent based on the theory of Lyapunov stability and linear matrix inequality. Markov jumps with uncertain rates of transitions are applied to describe the switch of topologies. Finally, a simulation example demonstrates the feasibility of the theory in this paper.

PACS: 05.45.Xt;02.30.Yy;89.75.-k;05.10.-a
Keyword:hybrid-triggered consensus;multi-agent system;time-delay and cyber-attacks;switching topologies
1. Introduction

In the recent decade, multi-agent systems have been extensively studied due to the wide applications in many fields, for example, unmanned aerial vehicle (UAV) cooperative control,[1,2] formation control,[3–5] etc. The consensus problem is a critical issue in multi-agent systems, consistency means that some variables of all agents in a multi-agent system must converge to the same state in the end. There are plenty of results about the consistency of multi-agent systems. In Ref. [6], the concept of partial component consensus in multi-agent system was proposed firstly, and then the consensus problem of partial component in a leader–following multi-agent system with the directed topology was investigated. In Ref. [7], the consensus problem of fractional-order multi-agent systems by sampled-data control based on directed topology with order was addressed. In Ref. [8], under the Markov switching topologies, the mean square consensus problems of multi-agent systems with and without non-linear dynamics were considered. And in Ref. [9], under asynchronous switching, the exponential consensus of multi-agent systems with both stochastic delayed and nonlinear dynamics was studied. In order to achieve consistency, generally a controller is established, according to the locally exchanged information, distributed control actions can be generated by the controller to guarantee that all agents agree on some physical quantities, for instance, the position or the velocity. It is worth mentioning that the information exchanges among agents are affected by the time delay. The network communication channel is limited, the agent cannot sample the state instantaneously, and the agent needs to spend time on related calculations, which both will cause the time delay,[10,11] so the designed controller must be robust. Moreover, there is often a situation that the communication topologies alter over time, i.e., switching topology,[12,13] owing to temporary communication losses or changes in the layout of the agents, which cause the transformation in the action of the consensus protocol. In this paper, the switching topology is also considered.

Because the event-triggered mechanism can greatly reduce information transmission among agents and the time of agent controller adjustment, its application is more and more extensive. In Ref. [14], the leader–following consensus problem of discrete multi-agent systems with parameter uncertainties was solved based on the event-triggered control strategies. In Ref. [15], aiming at the consensus problem of leader–follower under fixed and switching communication topologies, a decentralized event-triggered controller was designed. The event-triggered scheme provides a useful method to improve the communication efficiency compared to the time-triggered scheme. Nevertheless, most of the event-triggered mechanisms mentioned above always come at the expense of system performance, and it should usually strike a balance between the amount of communication and system performance. In multi-agent systems, optimizing data transmission methods remains a challenge. In an actual control system, the utilization of the communication bandwidth is sometimes low, and information transmission can be less in a certain period of time. For this system, neither the event triggering scheme nor the time triggering scheme can guarantee the best system performance. How to fully cope with this situation is still a challenge, therefore, we propose a hybrid-triggered mechanism,[16] which includes time-triggered scheme and event-triggered scheme, the purpose is to shorten this gap. There are plenty of results about the hybrid-triggered scheme. For example, the issue of quantized state estimation for neural networks with cyber-attacks was addressed with the hybrid-triggered mechanism in Ref. [17]. In Ref. [18], the hybrid-triggered scheme was proposed to exclude the Zeno behavior. The issue of filter design for neural networks with hybrid-triggered mechanism and cyber-attacks was studied in Ref. [19].

In recent years, the rapid development of the network has made the connection between the control field and the network more tight. The introduction of the network has improved the efficiency in many aspects of the control system, for instance, the processing speed of the control system becomes faster. Nevertheless, it also brings huge challenges, e.g., packet loss, cyber-attacks, network induced delay, etc, among which the cyber-attack is the hottest issue. Therefore, the majority of scholars began to consider cyber-attacks from the perspective of control theory. In Ref. [20], the issue of decentralized event-triggered control for neural networks was considered, where the neural networks had limited network bandwidth and were subject to cyber-attacks. In Ref. [21], Takagi–Sugeno fuzzy system’s quantized stabilization was addressed, and the stochastic cyber-attacks were considered under the hybrid-triggered scheme. In order to guarantee the security of the cyber physical system, a new risk assessment method was proposed to quantify the impact of cyber-attacks on the system in Ref. [22].

Inspired by the above mentioned works, we concentrate on the design of a hybrid-triggered consensus controller with random network attacks, time-varying delayed control inputs, and uncertain switching topologies. The main contributions of this paper are as follows.

1) The multi-agent system can be described by a linear system, linearizable system, and time invariant system. And a hybrid-triggered scheme is introduced, which includes time-triggered scheme and event-triggered scheme to reduce the burden of network transmission. Switching between the two strategies follows a random Bernoulli distribution.

2) Cyber-attacks are taken into account, the probability of a random network attack occurring also obeys the Bernoulli distribution and the time-varying delay of each agent control input can be non-differentiable and non-uniform.

3) Topologies switching has an uncertain transition probability, which is used to describe network system communication failures or changes in neighbor relationships.

It should be noted that the topology states do not necessarily contain a spanning tree, and the topologies switching can be regarded as a continuous-time Markov chain with an uncertain transition probability. Therefore, the Markov jump linear system can be used to replace the original multi-agent system, and the analysis of the original system consistency is completed by analyzing the stability of the Markov jump linear system. To solve the problem of uncertain conversion rate, we are inspired by Refs. [23]–[26]. As far as we know, there is no research on hybrid-triggered consensus for multi-agent systems with time-varying delayed control inputs, uncertain switching topologies, and stochastic cyber-attacks.

The remainder of this paper is organized as follows. In Section 2, knowledge related to graph theory is stated. The mathematical model of the multi-agent system is constructed in Section 3. And in Section 4, sufficient conditions are obtained to ensure the multi-agent system consistent. In Section 4, a simulation example is used to illustrate the validity of the theory in this paper. In the last section, the conclusion is given.

In this article, the following symbols are used: represents the n-dimensional Euclidean space, is n-order unit matrix, represents the transposed matrix of , the Kronecker product is denoted by , denotes that is a positive definite matrix, means the mathematical expectation of , and indicates a symmetrical part.

2. Basic theory of graphs

Graph theory is an important tool for studying multi-agent systems. Each agent can be represented as a node in graph theory. The information interaction among agents is represented as an edge in graph theory. A simple directed graph can be expressed as , for a multi-agent system with m agents, the node set is and the edge set is , where is the indicator set. is the adjacency matrix of graph , if and only if , and , the set of nodes vi neighbors is . The degree matrix is , where , and respectively indicate the degree of outbound and in degree of node vi, and , . If is an undirected graph, then is satisfied.

Therefore, the Laplacian matrix can be obtained as follows:

Then
The Laplacian matrix has an important property, i.e., 0 is one eigenvalue of and is its corresponding eigenvector.

3. Problem formulation
3.1. Consensus problem

Consider a multi-agent system with m agents, each with the following dynamic mathematical model:

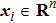
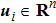
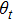
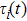
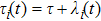
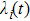
where represents the state variables of the i-th agent, the order of the agent dynamics is determined by n, and is the control input of the i-th agent. changes with time, and represents the connected agents of the multi-agent system at each instant of time t. is the time-varying delay that affects the control input of the i-th agent. 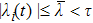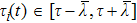Let , where τ is a constant, is disturbances that change with time, which satisfies , therefore is satisfied for all agents in the multi-agent systems.

The consensus controller in this paper is proposed as follows:

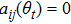
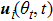
where is the constant matrix gain, determines the current topology state, for instance, if there is no communication between nodes i and j, then , and represents the control input based on the current topology of agent i. The initial conditions of agents’ states are shown as follows:
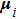
in interval , the function is arbitrary and corresponds to the set of initial conditions.

According to Ref. [27], the continuous time Markov chain determines the dynamics of the parameter 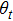, where the Markov chain has discrete states, the discrete states are given by a set of sets 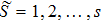, where s is the number of different topologies of the multi-agent systems. The expression of the probability transfer matrix 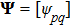is

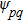
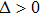
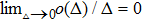
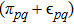
In the above formula, represents the probability of switching from topology p to topology q in interval at time t, for , holds, are the elements of the uncertainty transfer rate matrix
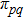
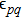
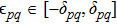
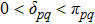
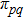
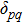
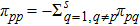
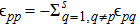
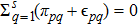
where represents an estimated value of the probability of switching from state p to state q, and represents an error of the estimated value. Here is unknown and with . It is obvious that both and are positive, and , , therefore, is obtained. Finally, let the initial distribution of the Markov chain be .

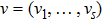
The dynamic mathematical model (3) and the consistency controller (4) of the agent are written in a compact form as follows:

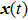
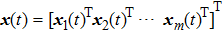
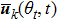
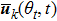
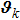
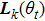
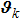
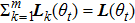
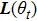
Here is a complete stacked state vector and , is the current input vector of the k-th agent, moreover, and are arranged in the same form, where is a column vector of nm dimension, its k-th term is one, and the other terms are zero, and is the Laplacian matrix of the current subgraph, only the edge pointing to the vertex is considered at this time. Notice that , where is the the Laplacian matrix which contains all the edges in the current topology .

The structure of the hybrid-triggered consensus for the multi-agent systems with time-varying delayed control inputs, uncertain switching topologies, and stochastic cyber-attacks is shown in Fig. 1. As is shown in Fig. 1, in order to save network resources, a hybrid-triggered mechanism consisted of time-triggered mechanism and event-triggered mechanism is introduced. The two triggered mechanisms are discussed below respectively.

Fig. 1. Structure of hybrid-triggered consensus for multi-agent systems with time-varying delayed control inputs, uncertain switching topologies, and stochastic cyber-attacks.

When the time-triggered mechanism is used in the hybrid-triggered mechanism, the sampled data will be transmitted as follows:[28]

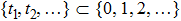
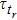
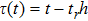
where tr are positive integers, which satisfy , is the corresponding delay caused by the network, and h is the sampling period. According to Ref. [29], let , therefore equation (10) can be rewritten as
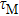
where , with being the maximum value of the delay.

According to Fig. 1, when the event-triggered scheme is chosen in the hybrid-triggered scheme, which is introduced to determine if the current measurement should be sent by comparing the latest sampled data with the error between two consecutive instants. The condition of the event-triggered scheme is given as follows:[30]

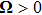
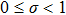
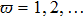
where , , and The expression of the threshold error is .

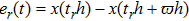
For the convenience of operation, according to Refs. [31] and [32], we can divide interval 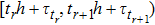into several subintervals. Suppose there is a constant ς that satisfies 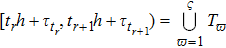, where 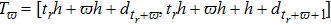, , 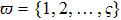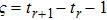. Define 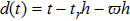, where .

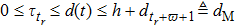The sampled signal in the event-triggered mechanism can be written as follows:

Remark 1 In the event-triggered control strategy, σ determines the frequency of event triggers. For example, σ=0 means that set 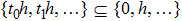will be released completely.

According to Ref. [32], in order to make full use of the limited network resources, the hybrid-triggered mechanism is introduced. The probability of switching between the time-triggered mechanism and the event-triggered mechanism is described by the random Bernoulli variable 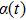. By combining Eqs. (10) and (13), 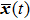in Fig. 1 can be written as follows:

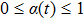
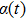
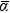
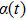
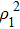
where . Here has the following properties: where is the expectation of , and represents the variance of .

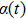
Remark 2 According to Eq. (14), when , , 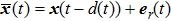i.e., the controller is under the event-triggered scheme, if 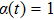, then , it illustrates that the time-triggered mechnasim is used for data transmission, i.e. the data is transmitted periodically.

Because of the introduction of networks in multi-agent systems, not only the delay caused by the network, but the stochastic cyber-attacks should be considered, in fact, the stochastic cyber-attacks are deception attacks, which will tamper with and destroy data from multi-agent systems in a network environment, which will result in each agent in the multi-agent system failing to receive correct and complete information, and degrade the performance and even cause system system crashes. In this paper, cyber-attacks are represented by a nonlinear function 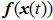. From Fig. 1, the control input is 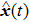, whose expression is

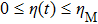
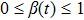
where is the expression of the cyber-attacks, and represents the time-delay of the cyber-attacks. Here is also a random Bernoulli variable, which indicates the probability of occurrence of the cyber-attacks and , .

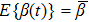
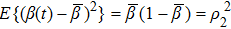
Therefore, by substituting Eq. (15) into Eq. (9), the consensus controller (9) can be rewritten as follows:

Remark 3 If 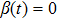, then 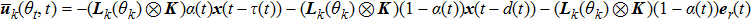, i.e., there is no malicious attack in the signal transmitted to the controller. When 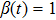, , 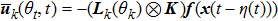the signals received by the controller are all cyber-attacks.

The closed-loop equation for the system can be obtained by substituting Eq. (16) into Eq. (8)

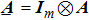
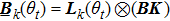
where and . Therefore, the definition of consistency is given as follows.

Definition 1 According to Ref. [33], when the consensus controller (4) is used and the hybrid-triggered scheme is introduced, multi-agent systems (3) can reach mean-square consensus under stochastic cyber-attacks and uncertain switching topologies. i.e., for all 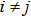, 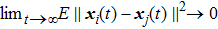is true in the mean square sense under all initial conditions and initial distributions 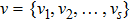of .

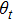An assumption and some lemmas are introduced in the following.

Assumption 1[34,35] The function of cyber-attacks 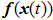satisfies the following inequality:

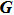
where is the constant matrix upper bound of the nonlinear function .

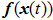
Lemma 1[36] For any scalars 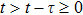and constant matrix , the following inequality holds:

Lemma 2 (Wirtinger inequality)[37] For any scalars 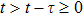and constant matrix 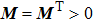, the following inequality is true:

where .

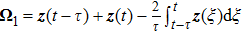
Lemma 3[38] A real number 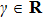and a matrix 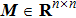are given, 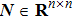is a symmetric positive definition matrix, then the following inequality is well defined:

Lemma 4[39] For any 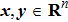with an appropriate dimension and an arbitrary symmetric positive definite matrix 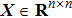, the following inequality holds:

3.2. Transformed multi-agent system

According to Refs. [40] and [41], the method of tree-type transformation is used to translate the consensus problem into a stability problem. This is finished by introducing new variables that represent the disagreement of variables

for . The above equations are written in compact forms as follows:
where , , , , and .

We calculate the derivative of time of Eq. (26), and obtain

substituting Eq. (17) into Eq. (32), then combining with Eqs. (29)–(31), and applying the fact that , , and to eliminate the terms that have , , , , and , then the following disagreement system (33) could be obtained:
where , , and .

Therefore, the consistency of system (17) is assessed by analyzing the stability of system (33) and Definition 1 can be rewritten as follows.

Definition 2 When the consensus controller (4) is used and the hybrid-triggered scheme is introduced, multi-agent system (3) can reach mean-square consensus under stochastic cyber-attacks and uncertain switching topologies if system (33) is stochastically stable in the mean-square sense, i.e., is true in the mean square sense under any initial conditions and initial distributions of the Markov chain.

Notice that for the convenience of derivation and calculation, is represented by in the following.

4. Consensus analysis

The following theorem gives the sufficient conditions that can guarantee the consistency of the multi-agent system with time-varying delayed control inputs, switching topologies, and stochastic cyber-attacks under the hybrid-triggered mechanism.

Theorem 1 Positive constant , , , , and the trigger parameter σ are given, where , , and are the upper of the time-delays. Discuss the multi-agent system (17) with , , and is defined as in Eq. (7), in formula (7), , where , , furthermore, the time-varying delay for . Then the system (17) achieves consistency in the mean square sense if there exist matrices , , , , , , , , , and such that the following inequalities hold :

where with

Proof The following Lyapunov–Krasovskii stochastic functional is chosen:

where corresponds to the state vector value and ,
with . Each matrix variable in each term of (36) is assumed to be positive definite, therefore, is positive definite.

According to Eq. (33), firstly, the following null term is researched:[42,43]

where , and and are both matrices that have appropriate dimensions. And we know the fact that

Combine Eq. (43) with Eq. (44) and the mathematical expectation is used at both ends of the equation simultaneously, so the following formula can be obtained:

with
Next, we apply Lemma 4, and have
Substituting Eq. (47) into Eq. (45), we can obtain
Furthermore, according to Eq. (36), we have
In the above formula, is discussed firstly. Based on Eq. (37) and appling Lemma 3, we have
we know and let , therefore the following inequality can be obtained:
We can also obtain
Applying Lemma 2 to Eq. (53), we have
with .

For , we have

where , . For in the above formula, we have
and , , are established. Then substitute Eq. (33) to Eq. (55) and apply Assumption 1 and the event-triggered condition, combine with Eq. (56) at the same time, finally, both ends of the inequality take mathematical expectations simultaneously, we can obtain
where and . We also have
according to Lemma 1, we can obtain

Therefore, the following inequality can be obtained:

where
and is defined in Theorem 1. We must know that and
Therefore, equation (61) can be rewritten as

In order to guarantee , for any the matrix within big parantheses in (64) must be negative, according to Schur complement, we have

where , causing the inequality (35), therefore, and assume that
and the generalized Itô’s formula is applied, we obtain
where is the random initial topology when the time is zero. So
which illustrates , therefore, system (33) is stochastic asymptotically stable in the mean square sense, i.e., the loop-closed system (17) finishes consensus in the light of Definition 2. This completes the proof.

5. Numerical simulation

In this section, a numerical example is given to illustrate the feasibility of the algorithm designed in this paper. According to Refs. [44] and [45], the following system is considered:

where is the position, b is the damping constant, and c is the spring constant. And the controller is designed as follows:
where k is the constant gain, and are used to calculate the desired constant distance . Substituting Eq. (71) into Eq. (70), we have

Therefore, formulas (72) and (73) have the same formats with Eqs. (3) and (4) respectively. Then apply Theorem 1, let . This paper designs three directed network switching topologies to establish intermittent communication: , , and . Figure 2 shows the three topologies, where is the time-varying delay.

Fig. 2. Multi-agent systems with three topologies , , and .

So the Laplacians are

In order to match the mentioned above, we extract some subgraphs from the Laplacians, which are associated with vertex vk, therefore we have

Notice that if there is no edge that points to vk in a topology, then its Laplacian is null. And if there is no spanning tree in , , and , then the system will not achieve consensus, however, the stochastic switching among the three topologies makes the consistency possible. The function of cyber-attacks is designed as , so we can obtain the upper bound , which satisfies Assumption 1.

Set and the uncertainty , and then we have

We have the sampling period h=0.002 s, the initial state , parameters , , , and . According to Theorem 1, we obtain that is a feasible solution, in this paper, we discuss this situation, i.e., , , which means that the probability of random network attacks is 12% and the multi-agent system applies the hybrid-triggered scheme. The response curve of is presented in Fig. 3, the response curve of is presented in Fig. 4. And the graph of cyber-attacks is shown in Fig. 5. Also, the graph of triggered moments of all agents and the released intervals of the event-triggered scheme is shown in Fig. 6. Figure 7 describes the switching probability between the two triggered strategies.

Fig. 3. The response curve of three agents’ states.
Fig. 4. The response curve of three agents’ velocities.
Fig. 5. The graph of cyber-attacks.
Fig. 6. The triggered moments and released intervals of the event-triggered scheme.
Fig. 7. The of the numerical example.

Figure 8 depicts the probability of stochastic network attacks. Furthermore, in Fig. 9, the switching between three topologies , , and is shown. Obviously, the results shown sufficiently demonstrate the effectiveness of the designed controller for multi-agent systems with time-varying control inputs, switching topologies, and stochastic cyber-attacks under the hybrid-triggered mechanism.

Fig. 8. The with and .
Fig. 9. The switching between three topologies , , and .

Since the hybrid-triggered mechanism is introduced in this paper, therefore its usefulness should be demonstrated. Comparisons between different triggered mechanisms are displayed in Tables 1 and 2. In Table 1, the number of the transmitted packets is recorded based on the sampling periods 0.1 s, 0.2 s, and 0.3 s respectively in T=[0,15]. Notice that the contrast should be evaluated under the same parameters.

Table 1.

Number of data transfers in different mechanisms.

.

According to Table 1, it is obvious that the amount of transmitted packets under the hybrid-triggered scheme in this paper are more than those of the event-triggered mechanism in Ref. [46] in the time period 0–15 s. Actually, when the control system has not reached the steady state, a large number of data packets need to be collected and analyzed, as shown in Fig. 3. And in Table 2, the time interval is T=[25,40] and the sampling periods are 0.1 s, 0.5 s, and 1 s respectively, the numbers of the transmitted packets under different triggered schemes are recorded. From Table 2, we find that the number of transmission packets of the hybrid-triggered scheme is significantly fewer than that of the time-triggered scheme when the control system gradually stabilizes, which illustrates that the introduction of the hybrid-triggered scheme can effectively reduce the number of transmitted data and alleviate the burden of the network.

Table 2.

Number of data transfers in different mechanisms.

.

Through the above analysis, we can see that the hybrid-triggered scheme proposed in this paper can adaptively gather the massive data in the initial stage to promote the control system to reach stability. After the system reaches the steady state, the hybrid-triggered mechanism can effectively reduce the number of transmitted data and save lots of network resources.

The simulation example shows that the proposed algorithm in this paper can be applied to the consistency verification of general linear dynamic systems with time-delay. Moreover, it can be proved that even if there are no spanning trees in all three topologies, the system can still converge. Finally, the probability of switching between the three topologies is uncertain and the method in this paper can analyze the consistency of the system under uncertainty and estimation. Therefore, the method can more flexibly ensure system consistency . Based on the above analysis, it can be seen that the multi-agent system finally achieves asymptotic stability and consistency, i.e., the hybrid-triggered consensus controller designed for multi-agent systems with network attacks, time-varying delays control inputs, and uncertain switching topologies is effective.

6. Conclusion

In this paper, the consistency problem of multi-agent systems with time-varying delay control inputs, switching topologies, and stochastic cyber-attacks under a hybrid-triggered mechanism is investigated. First of all, the hybrid-triggered scheme is introduced to alleviate the network burden. In order to be closer to the actual situation, the time-varying delay, switching topologies, and cyber-attacks are also considered, where the cyber-attacks are described by a Bernoulli variable. Secondly, the consistency condition that can guarantees the system consensus in the mean-square sense is given by a theorem even if there is no spanning tree in the communication topologies, and the theorem is obtained by using the theory of Lyapunov stability and linear matrix inequality. Finally, a simulation example is given to demonstrate the effectiveness of the method proposed in this paper.

Reference
1 Arbanas B Ivanovic A Car M Orsag M Petrovic T Bogdan S 2018 Auton Robot 42 1601 https://dx.doi.org/10.1007/s10514-018-9712-y
2 Beard R W Mclain T W Nelson D B Kingston D Johansonet D 2006 Proc. IEEE 94 1306 https://dx.doi.org/10.1109/JPROC.2006.876930
3 Wang J H Xu Y L Zhang J Yang D D 2018 Chin. Phys.B 27 040504 https://dx.doi.org/10.1088/1674-1056/27/4/040504
4 Luo X Y Han N N Guan X P 2010 Chin. Phys.B 19 100202 https://dx.doi.org/10.1088/1674-1056/19/10/100202
5 Cao J F Ling Z H Yuan Y F Gao C 2014 Chin. Phys.B 23 070509 https://dx.doi.org/10.1088/1674-1056/23/7/070509
6 Bin B W Zhong J M Yi W 2017 Acta Phys. Sin. 66 060201 (in Chinese) https://dx.doi.org/10.7498/aps.66.060201
7 Yu Z Y Jiang H J Hu C Yu J 2017 IEEE T. Cybernetics. 47 1892 https://dx.doi.org/10.1109/TCYB.2018.2879935
8 Miao G Y Xu S Y Zhang B Y Zou Y 2014 IMA J. Math. Control.I 31 151
9 Wu X T Tang Y Cao J D Zhang W B 2016 IEEE T. Cybernetics. 46 1817 https://dx.doi.org/10.1109/TCYB.2015.2453346
10 Li Y L Li H T Ding X Y Zhao G D 2019 IEEE T. Cybernetics. 49 3203 https://dx.doi.org/10.1109/TCYB.2018.2839892
11 Liu C J Liu G P 2018 J. Franklin.I 355 4198 https://dx.doi.org/10.1016/j.jfranklin.2018.04.003
12 Heitor J S Carlos R P dos S Fernando O S Luciano C A P Maurício D O Reinaldo M P 2016 IEEE T. Ind. Electron. 63 1258 https://dx.doi.org/10.1109/TIE.2015.2504043
13 Fang M Zhou C C Huang X 2019 Chin. Phys.B 28 010703 https://dx.doi.org/10.1088/1674-1056/28/1/010703
14 Liu X Y Sun J Dou L H Chen J 2017 J. Syst. Sci. Complex. 30 30 https://dx.doi.org/10.1007/s11424-017-6272-8
15 Cheng T H Kan Z Justin R K John M S Warren E D 2017 IEEE T. Automat. Contr. 62 5365 https://dx.doi.org/10.1109/TAC.2017.2693824
16 Liu J L Zha L J Cao J Fei S M 2016 IET Control TheoryA 10 2279 https://dx.doi.org/10.1049/iet-cta.2016.0392
17 Liu J L Xia J L Cao J Tian E G 2018 Neurocomputing 291 35 https://dx.doi.org/10.1016/j.neucom.2018.02.060
18 Zhang Y Yang Y Fan Y 2016 IEEE Control Conference July 27–29, 2016 Chengdu, China p. 7634 https://dx.doi.org/10.1109/ChiCC.2016.7554567
19 Liu J L Xia J L Tian E G Fei S M 2018 Appl. Math. Comput. 320 158 https://doi.org/10.1016/j.amc.2017.09.007
20 Zha L J Tian E G Xie X P Gu Z Cao J 2018 Inform. Sciences 457-458 141 https://doi.org/10.1016/j.ins.2018.04.018
21 Liu J L Wei L L Xie X P Tian E G Fei S M 2018 IEEE T. Fuzzy. Syst. 26 3820 https://dx.doi.org/10.1109/TFUZZ.2018.2849702
22 Huang K X Zhou C J Tian Y C Yang S G Qin Y Q 2018 IEEE T. Ind. Electron. 65 8153 https://dx.doi.org/10.1109/TIE.2018.2798605
23 Xiong J L Lam J Gao H J Daniel W C H 2005 Automatica 41 897 https://dx.doi.org/10.1016/j.automatica.2004.12.001
24 Xiong J L James L 2009 Int. J. Syst. Sci. 40 255 https://dx.doi.org/10.1080/00207720802300347
25 Zhang L X Boukas E K Lam J 2008 IEEE T. Automat. Contr. 53 2458 https://dx.doi.org/10.1109/TAC.2008.2007867
26 Zhang L X Boukas E K 2009 Automatica 45 463 https://dx.doi.org/10.1016/j.automatica.2008.08.010
27 Rohatgi V K 1983 Technometrics 25 116 https://dx.doi.org/10.1080/00401706.1983.10487838
28 Yue D. Han Q.L. Lam J. 2005 Pergamon Press, Inc. 999 1007 https://dx.doi.org/10.1016/j.automatica.2004.12.011
29 Tian E Yue D Peng C 2010 IET Control TheoryA 4 1478 https://dx.doi.org/10.1049/iet-cta.2009.0441
30 Yan H C Xu X L Zhang H Yang F W 2017 J. Franklin.I 354 3760 https://dx.doi.org/10.1016/j.jfranklin.2016.05.019
31 Yue D Tian E G Han Q L 2013 IEEE T. Automat. Contr. 58 475 https://dx.doi.org/10.1109/TAC.2012.2206694
32 Liu J L Zha L J Cao J Fei S M 2016 IET Control TheoryA 10 2279 https://dx.doi.org/10.1049/iet-cta.2016.0392
33 Miao G Y Xu S Y Zhang B Y Zou Y 2014 IMA J. Math. Control.I 31 151
34 Liu J L Wei L L Tian E G Fei S M Cao J 2017 J. Franklin.I 354 8490 https://dx.doi.org/10.1016/j.jfranklin.2017.10.007
35 Liu J L Xia J L Tian E G Fei S M 2018 Appl. Math. Comput. 320 158
36 Nian X H Gui W H Liu Y M 2006 Proceedings of the 6th World Congress on Intelligent Control and Automation June 21–23, 2006 Dalian, China p. 1422 https://dx.doi.org/10.1109/WCICA.2006.1712383
37 Seuret A Frédéric G 2014 Automatica 50 300 https://dx.doi.org/10.1016/j.automatica.2013.09.047
38 Xiong J Lam J 2009 Int. J. Syst. Sci. 40 255 https://dx.doi.org/10.1080/00207720802300347
39 Wang Y Y Xie L H De S C E 1992 Robust control of a class of uncertain nonlinear systems New York Elsevier Science Publishers B.V pp. 139–149
40 Savino H J Souza F O Pimenta L C A 2015 Int. J. Syst. Sci. 47 2475 https://dx.doi.org/10.1080/00207721.2014.998750
41 Sun Y G Wang L 2009 IEEE T. Automat. Contr. 54 1607 https://dx.doi.org/10.1109/TAC.2009.2017963
42 Mozelli L A Palhares R M Mendes E M A M 2010 IET Control TheoryA 4 2813 https://dx.doi.org/10.1049/iet-cta.2009.0210
43 Souza F O Palhares R M Barbosa K A 2008 IET Control TheoryA 2 1033 https://dx.doi.org/10.1049/iet-cta:20070343
44 Michael N Schwager M Kumar V Rus D 2014 Cardiologia 39 631
45 Schwager M Michael N Kumar V Rus D 2011 IEEE International Conference on Robotics & Automation May 9–13, 2011 Shanghai, China p. 3855
46 Chen P Qing L H Dong Y 2013 IEEE T. Fuzzy. Syst. 21 164 https://dx.doi.org/10.1109/TFUZZ.2012.2199994
47 Tian E Yue D Gu Z 2010 Fuzzy Set. Syst. 161 2731 https://dx.doi.org/10.1016/j.fss.2010.03.008