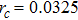† Corresponding author. E-mail:
There has been much interest in studying quasi-periodic events on earthquake models. Here we investigate quasi-periodic events in the avalanche time series on structured earthquake models by the analysis of the autocorrelation function and the fast Fourier transform. For random spatial earthquake models, quasi-periodic events are robust and we obtain a simple rule for a period that is proportional to the choice of unit time and the dissipation of the system. Moreover, computer simulations validate this rule for two-dimensional lattice models and cycle graphs, but our simulation results also show that small-world models, scale-free models, and random rule graphs do not have periodic phenomena. Although the periodicity of avalanche does not depend on the criticality of the system or the average degree of the system or the size of the system, there is evidence that it depends on the time series of the average force of the system.
Earthquake is a common phenomenon undoubtedly known to humans from earliest times. With the establishment of the plate tectonics theory, scientists started to understand the cause and nature of earthquakes. However, statistical studies appeared much earlier, urged by the necessity of predicting earthquakes.
Gutenberg and Richter realized that the energy released during the earthquake is increased exponentially with the earthquake magnitude.[1–3] This is the Gutenberg–Richter law. Larger earthquakes occur less frequently, the relationship being exponential (
Earthquakes are probably the most relevant paradigm of self-organized criticality (SOC) that can be observed by humans on the earth.[4–6] The SOC concept was introduced as a possible explanation for the widespread occurrence in nature of long-range correlations in space and time by Bak, Tang, and Wiesenfeld.[4,7]
In their sandpile model both the random, slow addition of “blocks” on a two-dimensional (2D) lattice and a simple, local, and conservative rule drive the system into a critical state where power law distributed avalanches maintain a steady regime far from equilibrium.
Olami, Feder, and Christensen (OFC) made an important contribution to the SOC ideas by mapping the Burridge–Knopoff spring-block model[8] into a nonconservative cellular automaton,[9,10] simulating the earthquake’s behavior. The model results in a power law distribution of avalanches similar to the Gutenberg–Richter law and also reproduces other characteristics of real earthquakes.[11]
In order to improve resemblance with the geological structure of the earth, and the presence of power law distribution of avalanches, the topology of connections between dynamical units plays an important role. In the literature, OFC models on different topologies have been explored previously. The anisotropic version,[12–14] random-neighbor version,[15–18] quenched random graph,[19,20] small-world,[21,22] scale-free,[23–26] random spatial network,[50] and other different topology models[50,50,50] have been investigated.
Earthquakes as SOC phenomena, in addition to the lack of success in predictability, have developed the idea that the crust is at a critical state where a minor perturbation can trigger an earthquake of any size and duration, making them inherently unpredictable.[50] However, foreshocks, aftershocks, and clustering properties indicate the existence of correlation between different events.[50,50,50,50,50] Many seismologists believe that large earthquakes are quasi-periodic,[50,50,50,50] but periodic behavior has appeared in theoretical models only as a special or as a trivial solution,[50,50,50] or as a result of a phase locking due to periodic boundary conditions (BCs),[50,50,50] or synchronized regions[50] in cellular automata.
However, a nontrivial quasi-periodic behavior in the avalanche time series with a period proportional to the degree of dissipation of the system has been discovered by Ramos et al. in 2006.[50] The correlation of time series of earthquakes can indicate impending catastrophic events and is considered to be possible to achieve prediction.[50,50,50]
In the aim of improving resemblance with the mechanical model they have introduced two variations in the OFC model. (i) Thresholds are distributed randomly following a narrow Gaussian distribution of standard deviation. (ii) Instead of assuming infinitely accurate tuning, a constant and finite force continually drives the system, but keeping the separation of time scales (relaxations are considered to be instantaneous) which is more realistic.
It is natural to think about whether there are quasi-periodic phenomena in other OFC models. And trying to find the mechanism for the emergence of quasi-periodicity.
In the present work, we first investigate the quasi-periodic behavior in a random spatial network. It is not like the original OFC model which exhibits SOC behavior for a wide range of dissipation values and the power-law exponent depends on the dissipation value, SOC can be excited only in the approximate conservative or the network is denser case.[9,50] There is not SOC on sparse spatial networks, due to the fact that spatial networks include many modules and the modular structure hinders the spreading of avalanches in the whole network. Connection degree is increased which enables energy transfer over a long range. The long-range energy transfer overcomes the effect of local modularity and SOC can be reached. An intuitive scenario is that there are no quasi-periodic phenomena in nonconservative random spatial network.
However, by analyzing the autocorrelation function and the fast Fourier transform for the avalanche time series, we show that there is a quasi-periodic phenomenon in the random spatial network. And we obtain a simple rule for a period that is proportional to the choice of unit time and the dissipation of the system. Although the periodicity of the avalanche does not depend on the criticality of the system or the average degree of the system or the size of the system, there is evidence that it depends on the time series of the average force of the system.
We have also explored other models in the present study. Cycle graphs and two-dimensional lattice models are in good agreement with the above laws, but small-world models, scale-free models, and random rule graphs do not have periodic phenomena.
The random spatial earthquake model was introduced by replacing the lattice model, in order to improve randomness and locality, which is more realistic.[50] In which sites are randomly placed on a plane and are connected locally. The network is built by two simple rules: (i) Randomly pick N sites on a square, whose width is L; (ii) Two sites are connected if the distance between each other is less than the connection radius rc.
The system average degree is 
Initialize all sites to a random value between 0 and Fth. When a site Fi reaches the threshold Fth, and a fraction 

The toppling of one site triggers an avalanche, that is, neighbors of this site may become unstable and toppling propagates in the network. The avalanche is over until all of the sites are below Fth. The number of toppling sites during an earthquake is defined as the earthquake size S. Then the driving to all sites recovers, a new avalanche is triggered. In a system of SOC, the distribution of earthquake sizes is a power-law function. We still adopt the above two changes: i) Thresholds are distributed randomly following a narrow Gaussian distribution of standard deviation σ=0.001. ii) A constant and finite force continually drives the system, 
We use the natural unit time for simplicity, that is an isolated block would need 104 steps from zero to reach the threshold 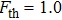
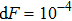

The autocorrelation function is defined as

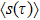
The original OFC model exhibits SOC behavior for a wide range of dissipation values and the power-law exponent depends on the dissipation value, and the original random spatial earthquake model exhibits SOC only in the approximate conservative or the network is denser case.[9,50] Figure
Figure
Next, we explore whether quasi-periodic phenomena will occur in random spatial earthquake models by calculating correlation functions. The system has parameters 
Surprisingly, the period under this random spatial earthquake model is consistent with that of the OFC model (see Fig.
We also see that the peak value of the correlation function decreases first and then increases with the increase of the dissipation coefficient in the random spatial earthquake model (see Fig.
It is not like that periodicity is as robust as criticality in OFC model, periodicity is independent of criticality in this model. The original OFC model exhibits SOC behavior for a wide range of dissipation values and the power-law exponent depends on the dissipation value, SOC can be excited only when the average degree is large and the system tends to conservation in this random spatial model. From the above research, we can see that this random spatial model, like the original model, has quasi-periodic behaviors under various conservative parameters. Therefore, periodicity and criticality are not dependent on each other.
Besides, the quasi-periodic behavior is robust for different system average degree 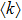
Moreover, we computed the fast Fourier transform (FFT) for the avalanche time series of both the random spatial earthquake model with 
We also discussed the mechanism of periodic phenomena. In general, the inherent complexity of SOC on networks makes analytical investigations almost always impossible. Although the periodicity of avalanche does not depend on the criticality of the system or the average degree of the system or the size of the system, there is evidence that it depends on the time series of the average force of the system.
The analysis of the average force of the system 

| Table 1.
Fitting details corresponding to Fig. |
Moreover, we find that the rule also holds for cycle graphs with k = 4 by analyzing the autocorrelation function for the avalanche time series in Fig. 

To illustrate the period depends on the time series of the average force of the system, we also analyze the average force time series of the anisotropic model, random rule graph, small-world network, and scale-free network, and find that these models do not exhibit quasi-periodic behavior. This is consistent with that we calculate the autocorrelation function to the avalanche time series for these models. Presumably because they have a larger variance of the degree distribution.
These numerical results indicate that periodicity is determined by the system average force. If there is quasi-periodic behavior in the time series of system average force, then there is also quasi-periodic behavior in the time series of avalanche. And the period is proportional to the choice of unit time and the degree of dissipation.
We have investigated how structure affects the quasi-periodic behavior of earthquake model. More specifically, we have shown that the quasi-periodic behavior is robust for structured models by the analysis of the autocorrelation function and the fast Fourier transform, including random spatial models, 2D lattice models, and cycles. We also obtained a simple rule for a period that is proportional to the choice of unit time and the dissipation of the system. It is not like that periodicity is as robust as criticality in OFC model, while the periodicity is independent of the criticality in this model. Next, we have explored other models. Although random spatial models, cycle graphs, and 2D spring-block models are in good agreement with the above laws, the small-world models, scale-free models, and random rule graphs do not have periodic phenomena. We have also explored the mechanism by which periodic phenomena occur. The periodicity of avalanche does not depend on the criticality of the system or the average degree of the system or the size of the system, however, there is evidence that it depends on the time series of the average force of the system. Since the quasi-periodic behavior exists in the time series of the system average force, the quasi-periodic behavior also exists in the time series of avalanche, and the value of the period is consistent. If the periodicity and self-organized criticality of earthquakes are taken as the basis, the random spatial model and the two-dimensional lattice model are most suitable.
We would like to thank Lin Zhou for helpful discussions.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] |