† Corresponding author. E-mail:
A new Willis aneurysm system is proposed, which contains the Atangana–Baleanu(AB) fractional derivative. we obtain the numerical solution of the Atangana–Baleanu fractional Willis aneurysm system (ABWAS) with the AB fractional integral and the predictor–corrector scheme. Moreover, we research the chaotic properties of ABWAS with phase diagrams and Poincare sections. The different values of pulse pressure and system order are used to evaluate and compare their effects on ABWAS. The simulations verify that the changes of pulse pressure and system order are the significant reason for ABWAS’ states varying from chaotic to steady. In addition, compared with Caputo fractional WAS (FWAS), ABWAS shows less state that is chaotic. Furthermore, the results of bifurcation diagrams of blood flow damping coefficient and reciprocal heart rate show that the blood flow velocity tends to stabilize with the increase of blood flow damping coefficient or reciprocal heart rate, which is consistent with embolization therapy and drug therapy for clinical treatment of cerebral aneurysms. Finally, in view of the fact that ABWAS in chaotic state increases the possibility of rupture of cerebral aneurysms, a reasonable controller is designed to control ABWAS based on the stability theory. Compared with the control results of FWAS by the same method, the results show that the blood flow velocity in the ABWAS system varies in a smaller range. Therefore, the control effect of ABWAS is better and more stable. The new Willis aneurysm system with Atangana–Baleanu fractional derivative provides new information for the further study on treatment and control of brain aneurysms.
The dynamic behaviors of chaotic systems have received increasing attention in recent decades. Some research revolved around the dynamic behavior of the models. In Ref. [1], a new model that can reduce the chaotic region was obtained by introducing a new variable. Wang et al.[2] proposed a pseudo-random coupling method which can accelerate the chaotic behavior of the full space. In Ref. [3], the complex dynamics of a geomagnetic field system were explored by introducing a non-smooth factor. The Willis aneurysm system is a biomedical chaotic system that has attracted researchers’ interest in recent years. Cerebral aneurysms are prone to rupture, which leads to high disability and mortality,[4] and the circle of Willis is a high incidence area of cerebral aneurysms. Therefore, it is necessary to predict and control the formation and growth of cerebral aneurysms by analyzing the chaotic dynamics of the Willis aneurysms system. The research on the Wills aneurysm system can be divided into the following three aspects: periodic solution, control method, and fractional order system.
In Ref. [5], Austin explained that a physical circuit can be used to simulate the flow of blood in a brain aneurysm, and a biomechanical model of Willis cerebral aneurysm was presented. This model reveals the non-linear relationship between the volumes and the pressure in the cerebral aneurysm. Some information to prevent rupture and swelling of the cerebral aneurysm was presented. However, the Austin model has limitations due to the omission of damping and certain constraints. Therefore, in Refs. [6] an [7], a Duffing equation with damping terms and forced external excitation was obtained by reanalyzing the analog circuit of Austin. Some studies were based on this new equation. Cao et al.[8] proved that the equation has at least one periodic solution under certain conditions. The condition of Devaney chaos in the Willis brain aneurysm model was obtained by the method of Melnikov function in Ref. [9]. The condition for the existence of the periodic solution of the system was obtained by Feng.[10] Nieto et al.[11] considered the existence of the solution of the periodic boundary value problem for the Willis aneurysm system.
The chaotic state of the Willis aneurysm system is harmful and chaos should be avoided as much as possible. In view of this problem, some scholars have discussed the control of the Willis aneurysm system. For the variable parameter Willis aneurysm system, based on the adaptive control idea, synchronization of two parameters of the Willis aneurysm system was obtained through the construction parameter adaptive law in Ref. [12]. Aiming at the control problem of the Willis aneurysm system with uncertainty, Peng et al.[13] proposed an adaptive fuzzy sliding mode control method. Sun et al.[14] studied a new Willis ring brain aneurysm mathematical model by introducing the antihypertensive drug excitation term function. The control method of antihypertensive drugs was presented.
All the above literatures only focussed on the integer-order Willis aneurysm system. Considering that the integer-order Willis aneurysm system has certain defects in describing the complex dynamics of blood flow, Cao et al.[15] studied a fractional order Willis aneurysm system based on Caputo derivative. This system was effectively controlled by the method of designing a controller and the drug excitation term function.
Many researches have analyzed the merits and drawbacks of fractional derivatives and put forward different definitions. Riemann–Liouville fractional derivative and Caputo fractional derivative are based on the power law functions. These two fractional derivatives have been in practice for a long time and applied to various practical problems successfully.[16,17] However, their kernel has a singularity, the kernel of Caputo derivative is a singular and the derivative of a constant is not zero in case of Riemann–Liouville fractional derivative.[18,19] Therefore, Caputo and Fabrizio[18] presented a new definition having non-singularity in the kernel to overcome the problem in 2015. Some research[20,21] revolved around the Caputo–Fabrizio fractional derivative. Besides the definition of Caputo–Fabrizio fractional derivative, Atangana and Baleanu[22] presented a new fractional definition in 2016. The Atangana–Baleanu (AB) fractional-order derivative is known to possess nonsingularity as well as nonlocality of the kernel, which adopts the generalized Mittag–Leffler function. The AB fractional derivative has all the benefits of the above fractional derivatives.[23] Recently, the Atangana–Baleanu fractional derivative has been applied in many fields, for instance, in biology and ecology,[24,25] electrical circuit,[26–28] fluid model,[29–32] groundwater,[33,34] and chaos theory[35,36] among many others.
Firstly, blood as a viscoelastic body[37] in soft matter[38] has the fluid viscosity and the elasticity of solids. Thus it has a complex flow pattern. Besides, the vascular system is a relatively complicated elastic piping system. Secondly, the brain aneurysm is a swelling area in the cerebral artery wall, and the system of Willis aneurysm involves the state and nature of the blood and vascular system. Therefore, the Willis aneurysm system has a complex dynamic mechanism. Finally, the asymptotic behavior of AB derivative makes it more advantageous than simple Caputo derivative in simulating complex phenomena.[39] The fractional order Willis aneurysm system with AB derivative has not considered before. Therefore, on the basis of the above three points, we consider a fractional order Willis aneurysm system using the new AB fractional derivative.
The main structure of this paper is as follows. The basic definitions of AB derivative are presented in Section
The definitions of the Atangana–Baleanu fractional derivative and integral are shown in this section. Besides, we have the conclusion that the AB fractional Willis aneurysm system with initial conditions is stable.


 |
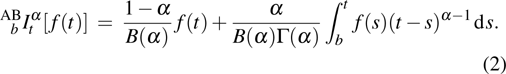 |
 |
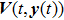
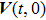
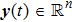

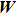
 |

 |
 |
 |
 |
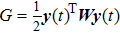
 |
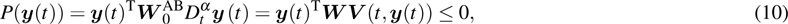 |
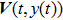
 |
 |
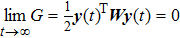
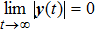
From Ref. [15], the Caputo fractional Willis aneurysm system is presented as follow:
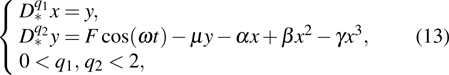 |
By changing the Caputo fractional differential of system (
 |
For the sake of simplicity, equation (
 |
 |
 |
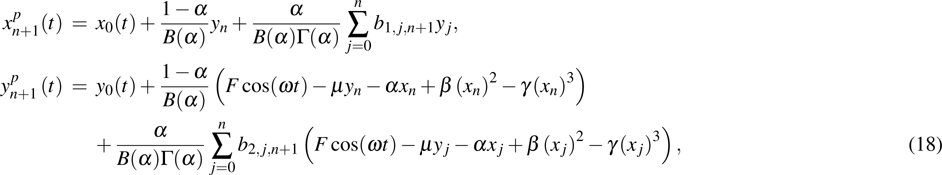 |
 |
 |
 |
 |
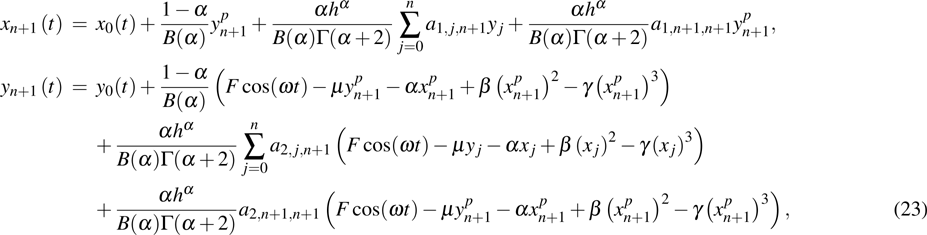 |
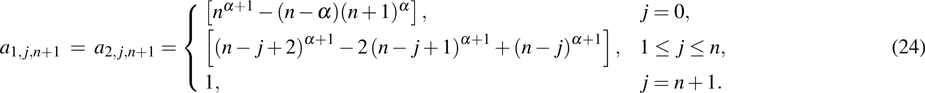 |
For system (
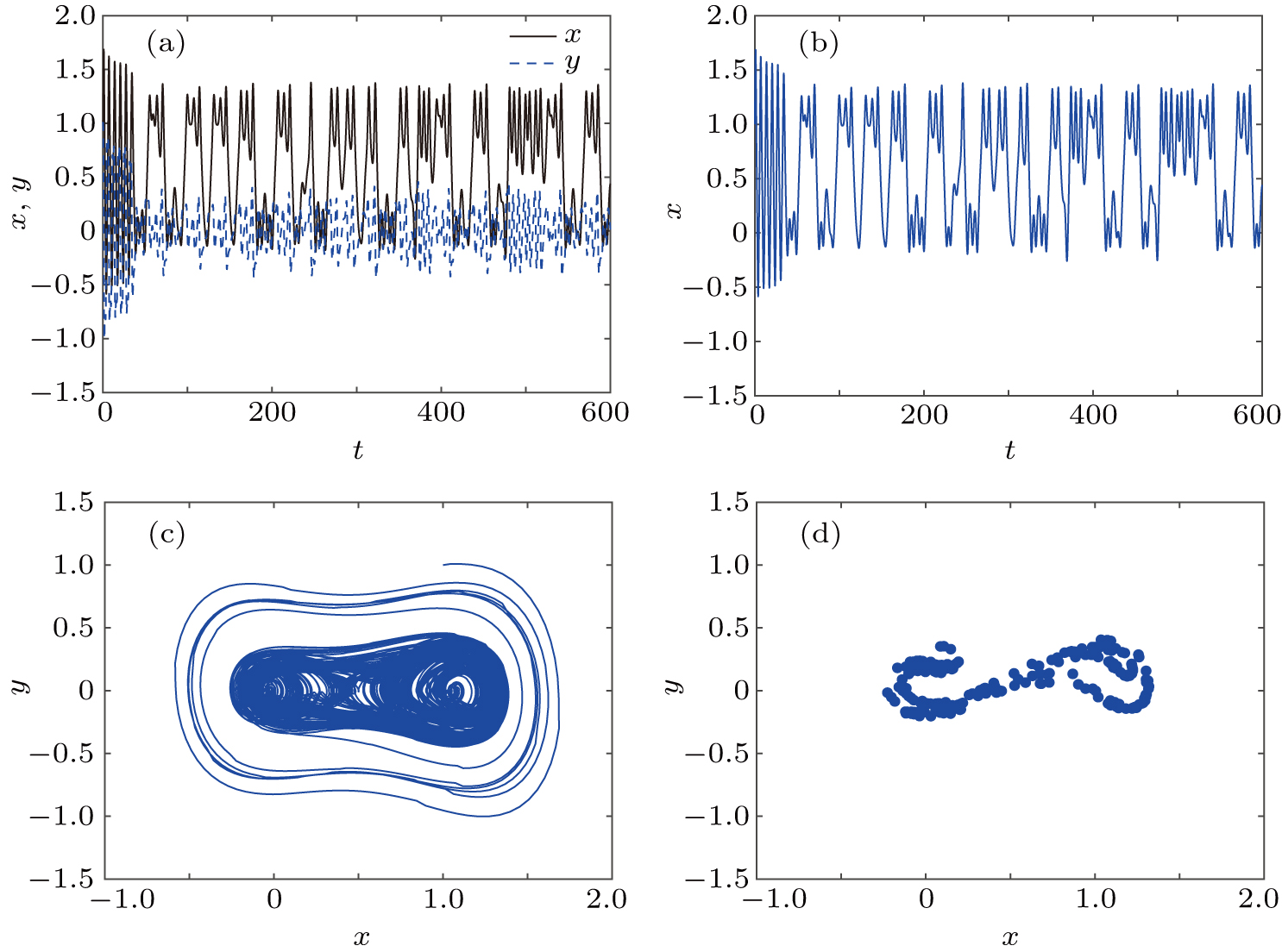 | Fig. 1. System order of ABWAS in the case of q1 =1.02 and q2 =0.97: (a) x–t and y–t curves, (b) time course, (c) phase diagram, (d) Poincaré section. |
Since systems (
In order to compare the results of FWAS and ABWAS when 





The following system is obtained with the parameters of q1 =1.02, q2 =0.97, α =0.9, β =3, γ =2, μ =0.1, ω =1:
 |

 | Fig. 4. Bifurcation diagram of system (
|
For system (

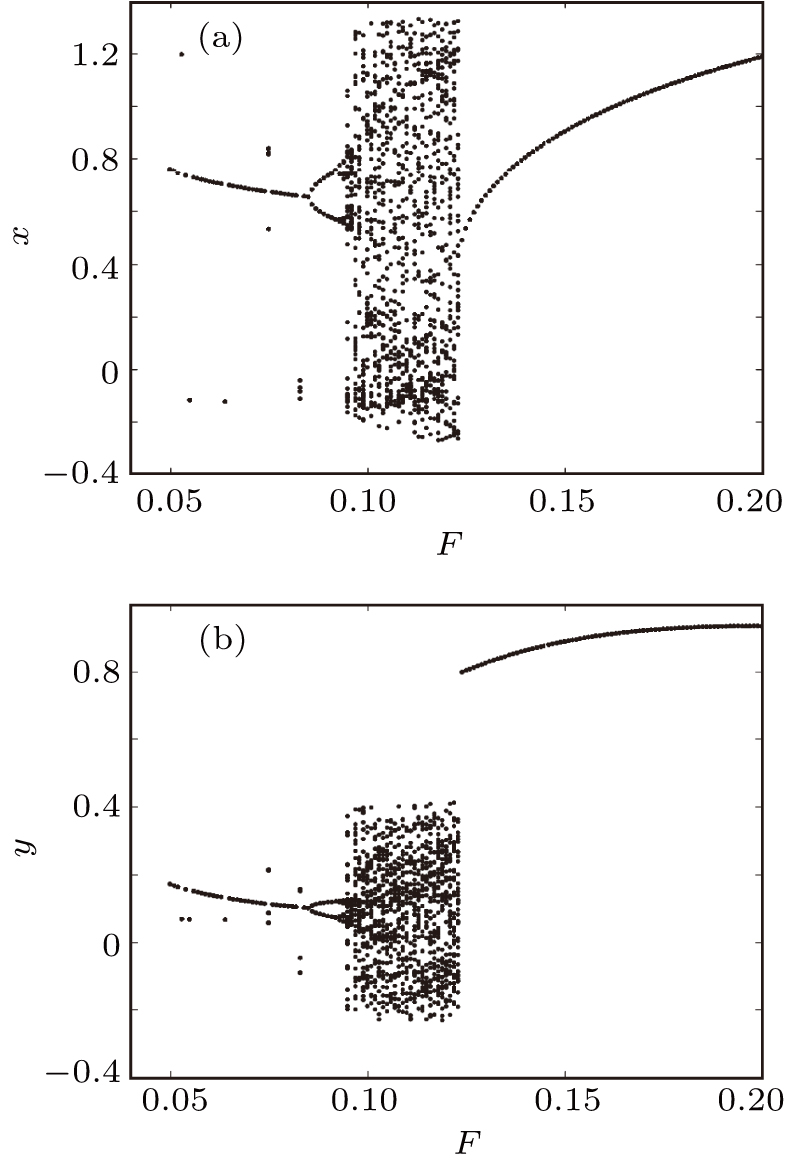 | Fig. 5. Bifurcation diagram of system (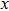
|
It can be seen that when the blood pressure is stable, the blood flow in the cerebral aneurysm is relatively stable. Conversely, the blood flow in the cerebral aneurysm is chaotic, and the cerebral aneurysm is prone to rupture.
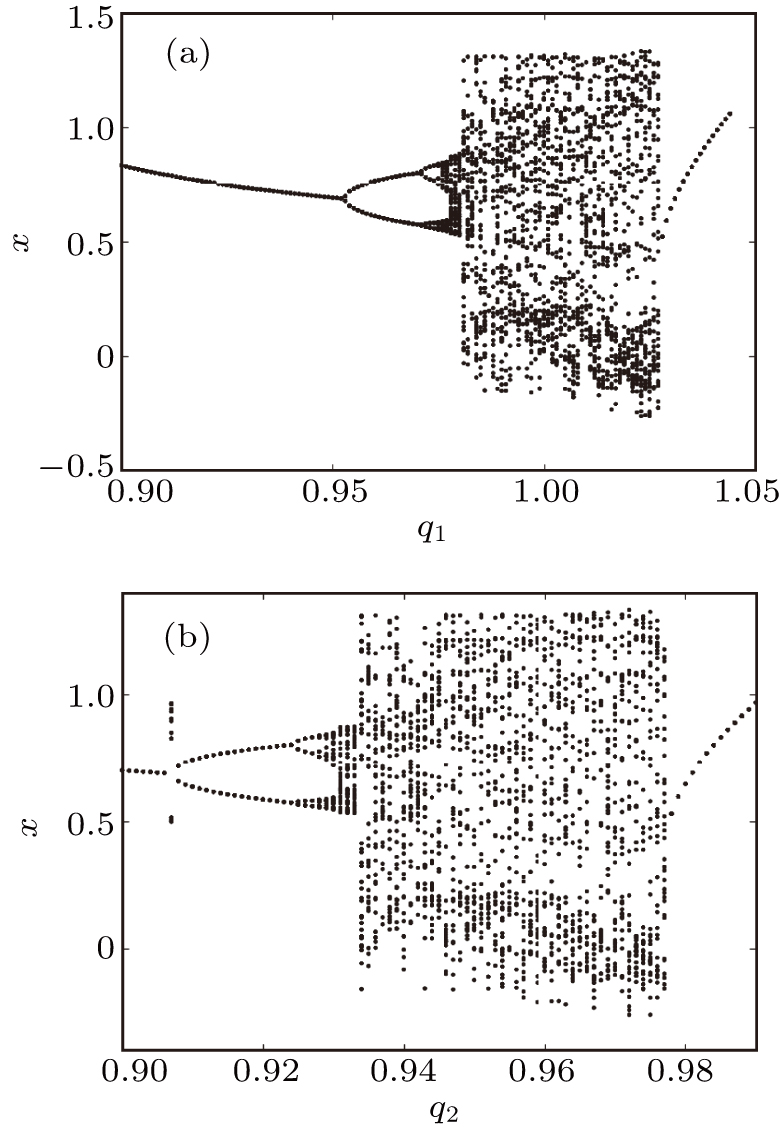
The effects of fractional order q1 and q2 on system (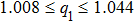

We can learn from Fig.
For system (

Compared with that of system (
The system order we select should help us to analyze the dynamic behavior of ABWAS. Further, the chaotic state of ABWAS shows unstable blood flow and rupture of cerebral aneurysms. Therefore, the system order that makes ABWAS in a chaotic state is our focus. It can be seen from Fig.
In this section, the parameters of system (
 | Fig. 8. (a) Bifurcation diagram of system ( |
In Fig.
The chaotic state of ABWAS is characterized by unstable blood flow. Furthermore, cerebral aneurysms are more likely to rupture in extremely chaotic speed state, which can lead to serious consequences such as headache, vomiting, and disturbance of consciousness. Therefore, the system (
With the same parameters as those in Section 3, the ABWAS with the initial value condition is obtained as follow:
 |
 |
In the quest to stabilize the system (
 |



 |
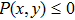
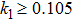

With 

 | Fig. 9. The control of ABWAS with controller ( |
The bifurcation diagrams of the controller-controlled ABWAS (
 | Fig. 10. Bifurcation diagrams of system ( |
Figure
In view of the fact that the Atangana–Baleanu fractional derivative can better describe the complex dynamics of blood flow, we establish a Willis aneurysm system based on the Atangana–Baleanu fractional derivative. The research results show that ABWAS is chaotic under the certain parameter values. Comparing to the bifurcation diagrams of order and pulse pressure of FWAS, the bifurcation diagrams of ABWAS show that less chaos occurs in the same ranges of order and pulse pressure. Therefore, we conclude that the order and pulse pressure have a significant effect on ABWAS.
With the increase of blood flow damping coefficient μ or reciprocal heart rate ω, the system tends to be stable. These results accord with the clinical treatment of cerebral aneurysms using the method of drugs or coils embolization. Therefore, the study of blood flow damping coefficient and reciprocal heart rate has certain significance for clinical diagnosis and treatment of cerebral aneurysms.
By designing a suitable controller based on the stability theorem, the blood flow velocity of the ABWAS can be stabilized in a short time. In addition, compared with the bifurcation diagrams of the controller-controlled Caputo fractional order Willis aneurysm system, under the same parameters, the blood flow velocity of the controller-controlled ABWAS changes within a smaller numerical interval. Therefore, the control effect on the ABWAS is better. This paper provides a theoretical basis for the study on the chaotic control and treatment of brain aneurysms.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 |