† Corresponding author. E-mail:
We studied quantum correlation and quantum entanglement of a quantum system in which a coherent state light field interacts with two qubits that are initially prepared in a separable and mixed state. The influence of mean photon number of the coherent field and distribution probability of the atom on the geometrical quantum discord and the negativity are discussed. Our results show that the mean photon number of light field and distribution function of the atom can regulate and control the quantum correlation and quantum entanglement.
The correlation is a universal phenomenon in the nature. Quantum correlation is a special nonclassical property of quantum systems, and quantum entanglement is an important quantum correlation in quantum information processing. As a resource, quantum entanglement plays a key role in many quantum information processing tasks.[1] The quantum entangled states with different degrees of entanglement will play different roles in quantum information processing. In the past few decades, many advances have been made in the study of quantum entanglement.[2–7] With the development of researches, it has been found that quantum entanglement cannot cover all non-classical correlations, that is to say, there is no entanglement but there is the correlation between quantum systems, so a more perfect measure of quantum correlation needs to be found. Whereupon, in 2001 year, Ollivier and Zurek[8] proposed the concept of quantum discord. It introduces a new measure of all the quantum correlations of the system. The quantum discord characterizes non-classical correlations in quantum mechanics, similar to the entanglement, quantum discord can also capture the fundamental features of quantum states. Since the quantum discord was put forward, and soon it has been found the non-classical correlations are more widespread than the entanglement. The quantum discord was investigated quite intensively in recent years.[9–16] In practice, due to the quantum discord maximizing involved in the calculation process, it is difficult to get the analytic expression. At present, only two-body Bell diagonal state, X-type 2×2 mixed state and highly symmetric manuscript dimensional state can be analyzed and calculated, this has greatly hindered the research progress of the quantum discord. In order to overcome this difficulty, Dakic et al. put forward a new method of measuring quantum correlations in 2010 year,[17] namely the geometrical quantum discord (GQD). The GQD is a definition of the smallest Hilbert–Schmidt distance between a given state and quantum discord for zero state. So far, some new research progress has been made for the GQD in different quantum systems.[18–22] However, the GQD and the negativity under the association measure of separable and mixed quantum correlation problems are rarely studied. Therefore, in this paper, we investigate the quantum correlation and the quantum entanglement in a system of separable and mixed qubits interacting with the coherent state light field. We use the GQD to measure the quantum correlation between separable and mixed qubits, and the negativity to measure the quantum entanglement between the separable and mixed qubits, respectively. This paper is organized as follows. In the next section, we give our theoretical model and density matrix of the quantum system. In Section
We consider a quantum system composed of two separable and mixed qubits interacting with a cavity field simultaneously, and suppose that the two qubits are coupled to the a cavity field with the coupling constant g. Under the rotating wave approximation, the Hamiltonian of the system can be written as 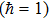
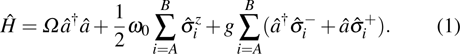 |
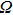

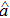
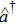
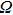
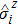

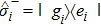
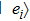
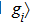
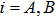
In the interaction picture and resonance case 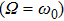
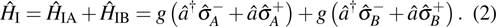 |
When the two qubits are prepared in 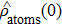

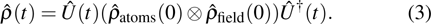 |
For the interaction of two qubits with a cavity field, using Eq. (
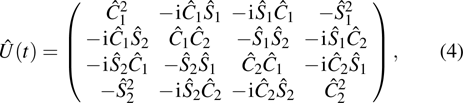 |
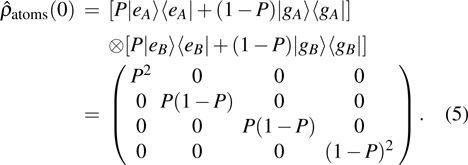 |
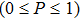
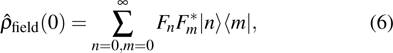 |
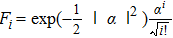
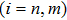
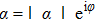

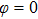
According to Eq. (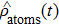
 |
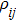
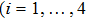
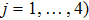
For a two-body quantum systems, the quantum correlation can be defined in terms of the GQD[17]
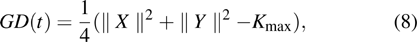 |
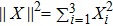
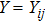
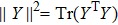
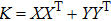
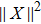

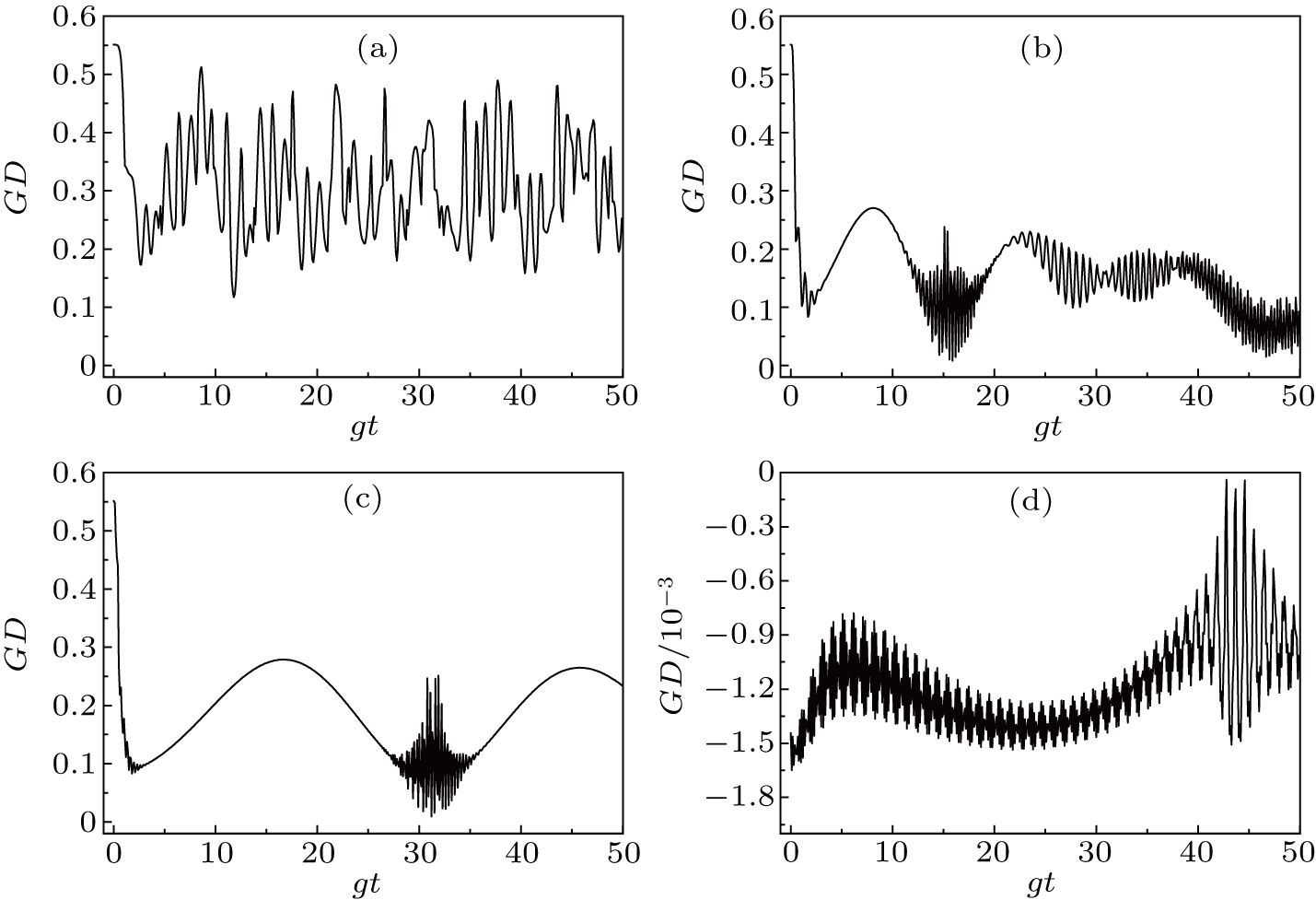
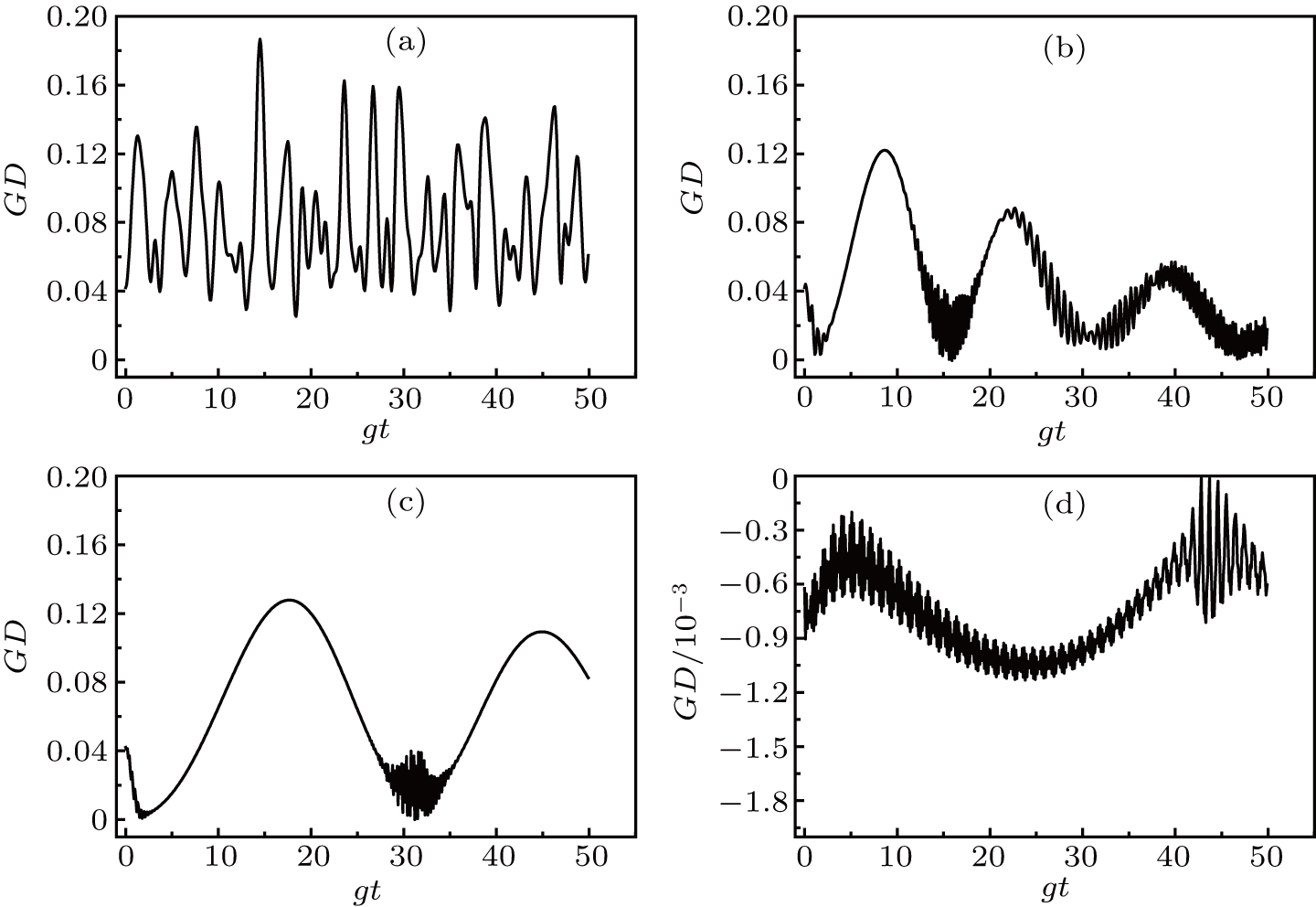
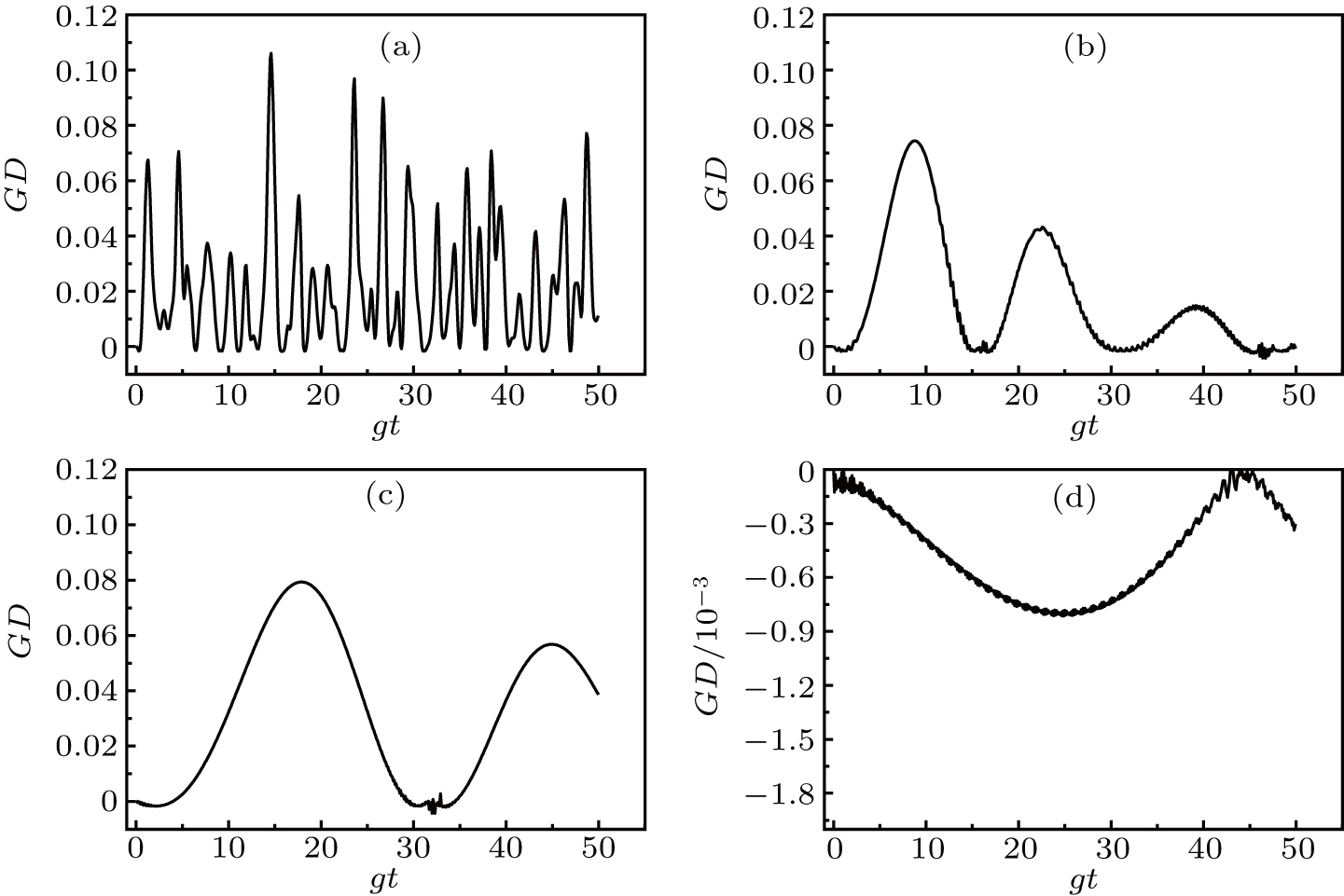
For an atomic system initially in a separable and mixed qubits, we select different atomic distribution probabilities in this paper, so are different initial states. In the numerical processing, the evolution of the GD(t) is prominent. The temporal evolution of the GD(t) is shown in Figs.
When P = 0, and two qubits are initially in the ground states, the evolution characteristics of the GD(t) versus different 
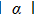
When P = 0.25, the two qubits are initially in the mixed states. Its time evolution curved lines of the GD(t) are also similar, which are shown in Fig.
Finally, we choose the two qubits are initially in the maximally mixed states, that is to say when P = 0.5. The time evolution of the GD(t) is shown in Fig. 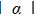
In summary, it can be seen from Figs. 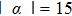
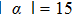
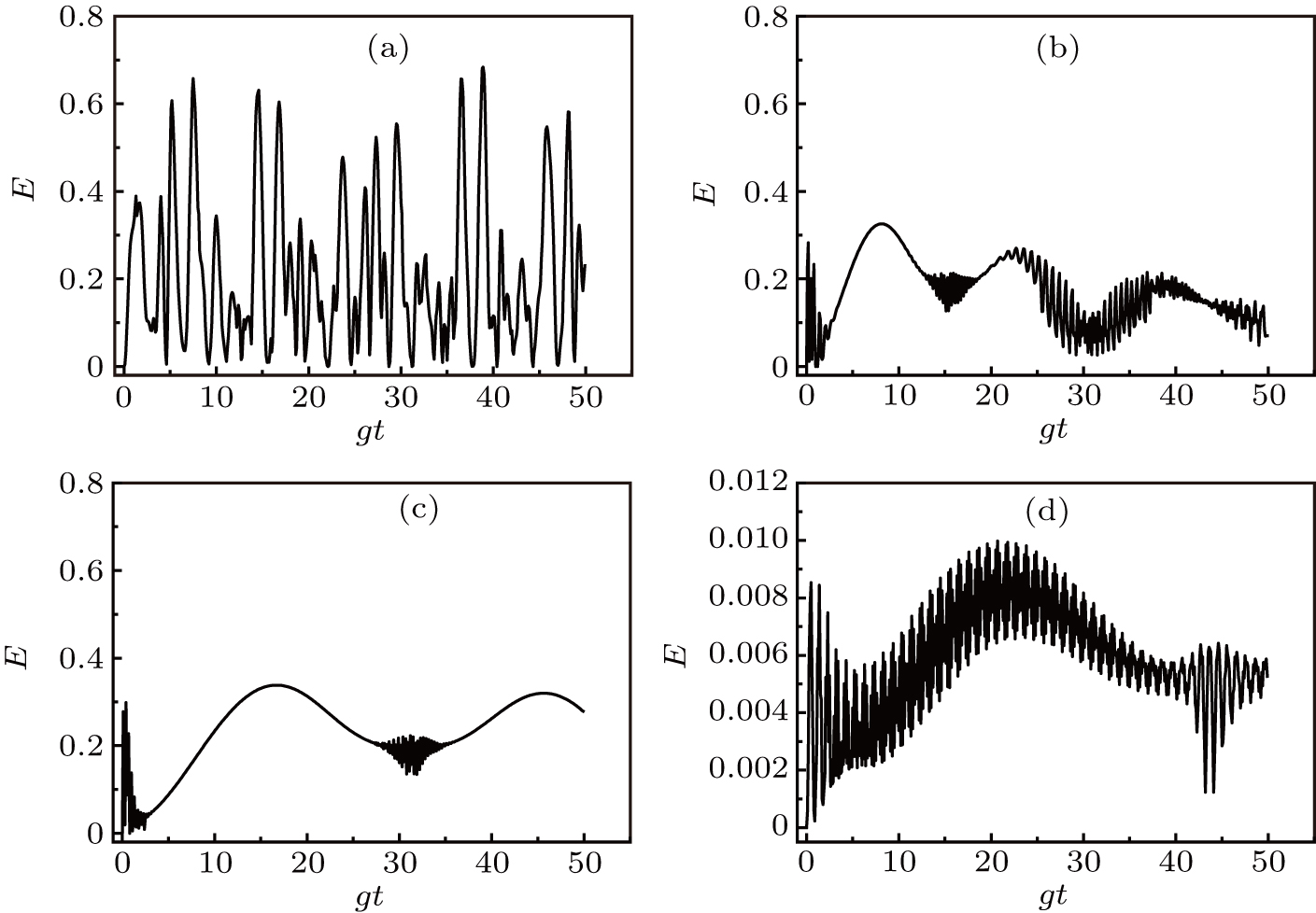
On the other hand, the negative eigenvalues of partial transposition of density matrix is a measurement of the degree of entanglement between the two subsystems. Also known as the negativity. The defined measurement by Peres[2] is
 |

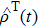
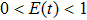

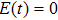
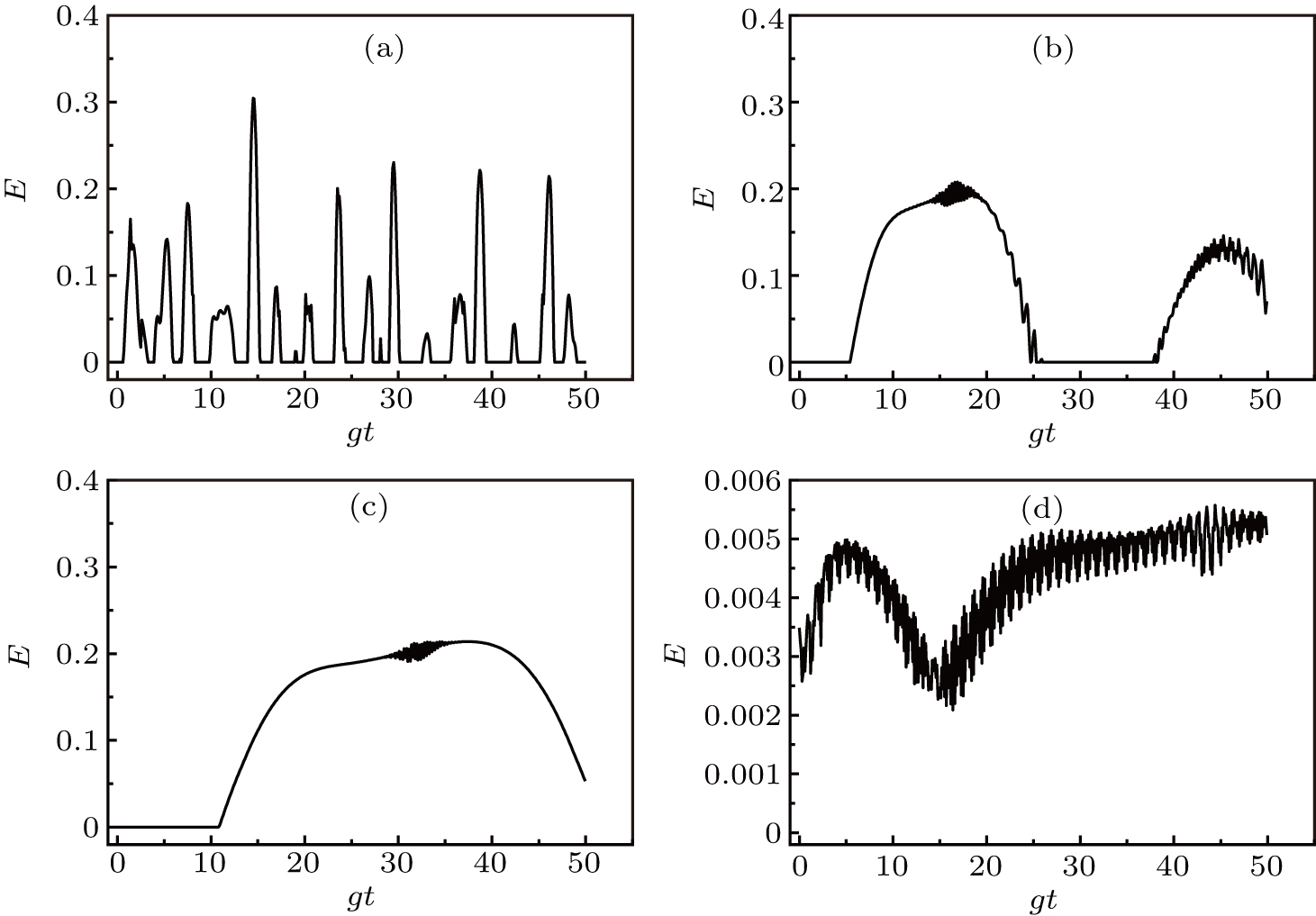
Here, the parameter selection is the same as in Subsection 3.1, the time evolution of E(t) is shown in Figs.
As shown in Figs.
In this paper, quantum correlation and quantum entanglement evolution properties of the coherent light field interacting with the two qubits that are initially prepared in a separable and mixed state have been studied in details. The influence of the mean photon number and the atomic distribution probabilities on the temporal evolution of the quantum correlation and quantum entanglement between two qubits are discussed, respectively. The results show that the evolving curve of the quantum correlation and quantum entanglement can be changed by the mean photon number, and the phenomena of negative quantum correlation and entanglement sudden death and generation are presented.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] |