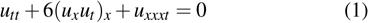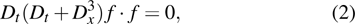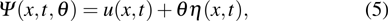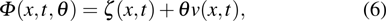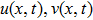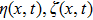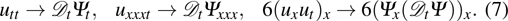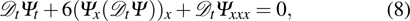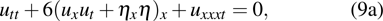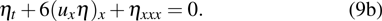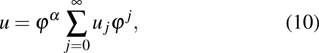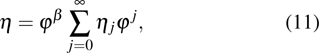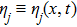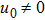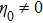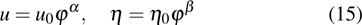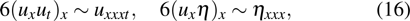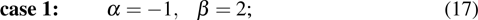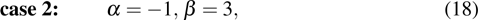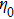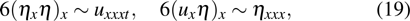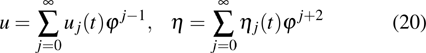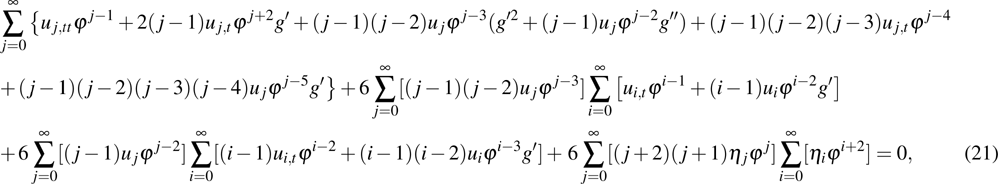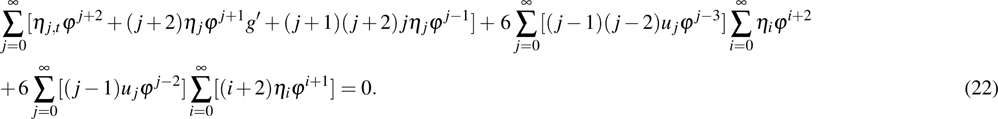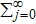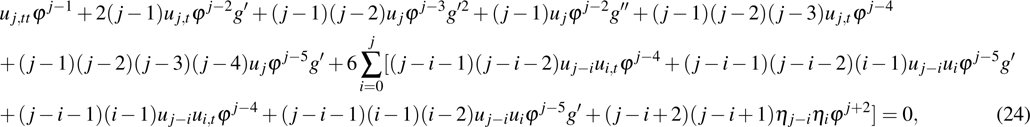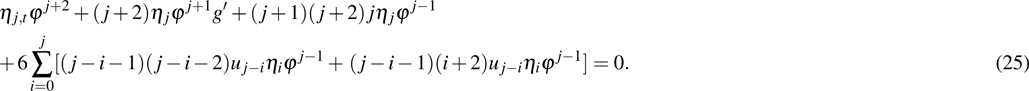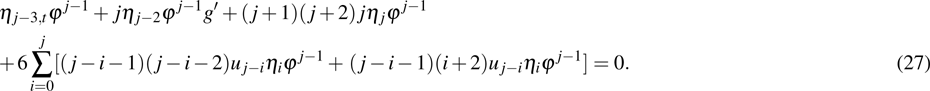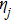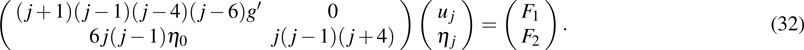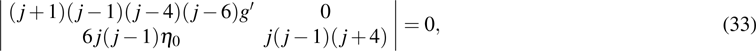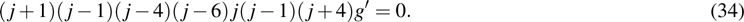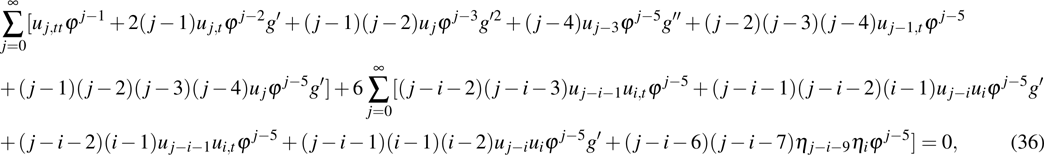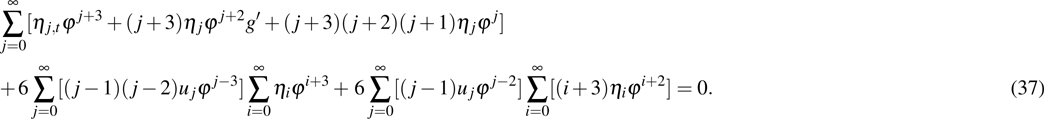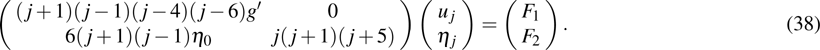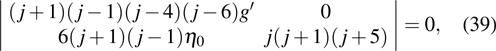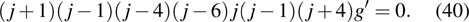Department of Physics, Shaoxing University, Shaoxing 312000, China
† Corresponding author. E-mail:
junyu@usx.edu.cn
1. IntroductionThe conception of supersymmetry was first proposed by physicists aiming to unify all field theories into one,[1–3] inspired by which mathematicians developed many efficient methods to construct supersymmetric systems, often with good integrability. For instance, the supersymmetric versions of the Sine–Gordon equation, the Kadomtsev–Petviashvili (KP) hierarchy, the Korteweg–de Vries (KdV) hierarchy, the Boussinesq equation, and a number of other systems were established and their soliton solutions were obtained by different methods.[4–10]
It is well known that for bosonic systems, through Painlevé analysis not only integrable properties could be investigated, but also Bäcklund transformations, Hirota’s bilinear form, and even Lax representations of many nonlinear systems could be obtained.[11,12] The Painlevé integrability demands that there exist Laurent series on open sets of the complex time variable solutions and these solutions should be consistent, or match on the overlapping pieces of the sets on which they are defined. In other words, this notion of integrability is the existence of a meromorphic solution. Painlevé analysis has also been extended to super nonlinear systems to study the super KdV equation[4] and many other important nonlinear systems.[8,13–18]
It is well known that the Ito equation
can be transformed into the bilinear form
by the transformation
In this paper, we concentrate on the Ito equation (
1) to find its supersymmetric form and take the standard Painlevé test by using Kruskal’s simplification. Different properties of the Ito equation (
1) or its different form of variation have been discussed in many literatures. Ito has obtained the first explicitly expressed
N-soliton solutions of Eq. (
2). For the Ito integro-differential equation, Ebadi
et al.[19] obtained its
N-soliton solutions and conserved quantities. The integrable properties of this equation such as the nonlinear superposition formula, Kac–Moody algebra, bi-Hamiltonian structure have also been found in Refs. [
20]–[
22].
This paper will be devoted to the integrability of the supersymmetric Ito (sIto) equation. In the next section, we supersymmetrize the Ito equation by simply introducing a new Grassmann variable and a superderivative. In Section 3, a detailed Painlevé test is carried on the supersymmetric Ito equation, which is categorized into to two cases. The last section is devoted to a short summary and discussion.
2. Supersymmetrization of the Ito equationIn order to supersymmetrize the Ito equation (1), in the first step, we have to introduce some new independent variables by extending the variable t to a doublet
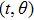with θ being an Grassmann odd variable. So the original independent variables (x,t) are generalized to super case
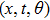and the associated superderivative is
In the next step, we have to extend the dependent variable u(x,t). There exist two ways to do so, one of which is to introduce a bosonic superfield
and the other one is to introduce a fermionic superfield
where
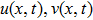
and
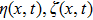
are Grassmann even and odd variables, respectively.
In this paper, we concentrate on the first extension way. To accomplish the symmetrization procedure, we first multiply each term of the Ito equation (1) by the Grassmann odd variable θ and then rewrite them in terms of the corresponding superfields, i.e.,
By substituting, we finally obtain the supersymmetric Ito equation in the form
which can be written in component form by using Eq. (
5) as
3. Painlevé integrablity of the supersymmetric Ito equationTo explore the Painlevé integrability property of the Ito Eq. (1), we start with the following series expansions for the field variables:
where
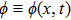
is a bosonic singular manifold, and
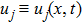
and
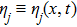
are bosonic and fermionic functions, respectively. There exist various concrete methods to carry out the Painlevé test, such as the Weiss–Tabor–Carnevale approach,
[12] the Kruskal’s simplification, the Conte’s invariant method,
[23] and the Lou’s extended approach.
[24] Here we use Kruskal’s simplification method, which means we take the following simplifications:
with the additional condition
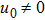
and
.
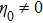
To determine the constants α and β, we use the leading order analysis, i.e., substituting
into Eqs. (
9a) and (
9b) and balancing the dispersion term and nonlinear term
two solutions are obtained,
where
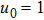
and
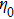
is an arbitrary function in both cases.
While for another case of balancing nonlinear terms and dispersions terms
there is no solution and should be abandoned.
The next step is to determine the resonant points, which should be discussed for the two cases, respectively. For case 1, we substitute Eqs. (10) and (11) with Eqs. (12), (13), (17), i.e.,
into the supersymmetric Ito equation (
9) and obtain
To simplify the above equations, we use the following identities:
and extract the common summation
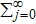
to obtain
Now by collecting the coefficients of
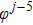
and
and making them to be zero, we respectively obtain
For Eqs. (
26) and (
27), selecting the terms containing
uj and
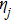
and leaving other terms be considered as one term, we obtain
where
,
.
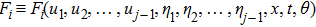
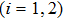
By substituting
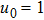into Eqs. (28) and (29), they transform into
which can be written in matrix form
The resonant points are determined by making the determinant of the coefficient matrix in Eq. (32) to be zero, i.e.,
which leads to
For case 2, we substitute Eqs. (10) and (11) with Eqs. (12), (13), (18), i.e.,
into the supersymmetric Ito equation (
9) and respectively obtain
Using the same identities as in Eq. (
23) and performing similar procedures as in case 1, we obtain
We have the determinant equation
which leads to
For case 1, the resonant point arises at j=−1, 1, 4, 6, 0, −4. It is known that j=−1 corresponds to the arbitrariness in the location of the singularity surface. The other four non-negative resonance values correspond exactly to four arbitrary functions
and the other lower order coefficients satisfy
For case 2, a similar conclusion holds, which is omitted here.
From the above result, we know that equation (9) passes the Painlevé test. Therefore, the sIto system is a candidate for the integrable supersymmetric equation.
4. Discussion and conclusionIn summary, the supersymmetric Ito equation is constructed by introducing new Grassmann odd independent variables and a new bosonic super field. A detailed Painlevé test using Kruskal’s simplification method is performed on the sIto equation, it demonstrates that this equation could pass the Painlevé test and we call it possess Painlevé integrability. The methods to supersymmetrize classical equations and Painlevé test procedure are applicative to abundant other integrable systems, meanwhile through some Painlevé analyses we can obtain Lax pair and Bäcklund transformations, which deserve to be studied in the future.
