Cite this Article
Gambhir Monica, Prasad Vinod. Non-perturbative multiphoton excitation studies in an excitonic coupled quantum well system using high-intensity THz laser fields. Chinese Physics B, 2019, 28(8): 087803  
Permissions
Non-perturbative multiphoton excitation studies in an excitonic coupled quantum well system using high-intensity THz laser fields
Gambhir Monica1, †, Prasad Vinod1, 2
Department of Physics, Swami Shraddhanand College, University of Delhi, Delhi 110036, India
Departmento de Quimica, Universidad Autónoma Metropolitana, San Rafael Atlixco No. 186, Iztapalapa, México DF 09340, México

 

† Corresponding author. E-mail: monicagdu@gmail.com

Abstract

Multiphoton excitations and nonlinear optical properties of exciton states in GaAs/AlxGa1−xAs coupled quantum well structure have been theoretically investigated under the influence of a time-varying high-intensity terahertz (THz) laser field. Non-perturbative Floquet theory is employed to solve the time-dependent equation of motion for the laser-driven excitonic quantum well system. The response to the field parameters, such as intensity and frequency of the laser electric field on the state populations, can be used in various optical semiconductor device applications, such as photodetectors, sensors, all-optical switches, and terahertz emitters.

PACS: 78.67.De;78.67.-n;71.35.-y
Keyword:quantum well;excitons;terahertz;non-perturbative;multiphoton;laser;Floquet
1. Introduction

The terahertz (THz) regime of the electromagnetic spectrum is commonly recognized by the frequency range of 0.1 THz–30 THz.[1] In the last few decades, progressive growth of various experimental techniques to control the dimensions and complexity of nanostructures as well as the development of various THz sources such as free electron lasers,[2,3] quantum cascade lasers,[4] and the accelerator-based THz light sources that can emit radiation with peak power in the megawatt region[5] has led to the expansion of interest of researchers to study the optical properties of quantum nanostructures. Immense literature work has been devoted to the optical studies of quantum nanostructures using THz sources that have profound utilization in the fields of pharmaceutical and biomedical,[6] industrial, environmental and meteorological applications,[7] security systems,[8] detecting explosive agents,[9] etc. Notably, semiconductor quantum wells have been probed for the terahertz detection using intersubband transitions in GaAs/AlGaAs quantum wells, which has led to the evolvement of new devices operating in the infrared and far infrared regions such as far-infrared photo-detectors,[10] all-optical switches,[11] high-speed electro-optical modulators,[12] and infrared lasers.[13]

The structure parameters of the quantum structures, especially the shape of the quantum well and potential specifics, are important criteria to study the optoelectronic properties covering a wide spectral range.[14–19] In quantum wells structures, light irradiation creates the electrons and holes in the quantum well, which are often bound to form neutral excitons. The suitability of THz laser devices to study excitonic interactions can be asserted on the fact that intraexcitonic energy spacing between exciton states is comparable to the wavelength range in which the THz laser devices operate. At present, there are various experimental techniques that may be used to investigate the excitonic optical properties, such as photoluminescence (PL) spectroscopy, near-infrared (NIR) absorption spectroscopy, etc., using THz light sources. The analysis has many practical applications. For instance, Wagner et al. observed the near-infrared transmission of a semiconductor multiple quantum well probed under intense terahertz illumination and provided a scheme for an ultrafast, normal-incidence optical modulator.[20] Galbraith et al. experimentally studied PL and terahertz absorption spectra of a GaAs multiple quantum well, indicating the experimental detection of a population of bound exciton.[21] Rice et al. experimentally studied exciton transitions mediated by Coulomb interactions in photoexcited semiconductor quantum wells. The experimental evidence of the PL emission acted as a good fingerprint to identify excitonic populations.[22] Su et al. demonstrated the use of THz driven gated double quantum well for voltage-controllable wavelength converter.[23]

In this paper, we introduce a four-level excitonic quantum well (EQW) system made by two GaAs/AlxGa1−xAs quantum wells, and study the multiphoton transitions using a periodic laser field and static electric field. Perturbative methods have been used to study the interaction of high-intensity lasers with EQW under the influence of dc electric field as well.[24,25] The perturbation theory has the disadvantage that it declines when the radiation intensity is too large or when the radiation frequency is close to one of the eigenfrequencies. Further, the perturbative methods are applicable when the energy difference between initial and final transition states is very large as compared to the corresponding transition matrix element. An exact, nonperturbative method, based on Floquet analysis primitively introduced by Shirley,[26] has been pursued for the problem. Using this approach, the Floquet states are obtained in the Fourier domain. We provide the study of the variation of Floquet states and quasienergies as a function of the laser field parameters (strength and frequency) as well as dc electric field. The method has been successfully applied in the molecular as well as in quantum heterostructures[27–29] to study the evolution of states. The quantum wells are the budding candidates for these studies as they have the advantage in adjustable design, prolong dephasing times, considerable dephasing rates (∼10 ps), tractable interference strength, and large electric dipole moment as compared to other quantum well structures.

Although the primitive interest for such studies is theoretical and various physical applications of the problem have been theoretically explored earlier in quantum heterostructures such as controlling electron transport in few-electron quantum dots to fabricate a quantum switch,[30] production of currents in an ac-driven quantum dot,[31] absorption and the nonlinear sideband generation,[32] and low-frequency dynamics,[33] these results may be experimentally observable. Floquet bands and quasi-energies were interpreted by the spectroscopic techniques such as pump-probe experiments and time and angle-resolved photoemission spectroscopy (Tr-ARPES) in graphene[34] and in monolayer transition metal dichalcogenides (TMD).[35] To the extent of our knowledge, no such experimental studies are available in excitonic quantum nanostructures. We hope that our theoretical results will stimulate experimental researchers to carry out such experiments in excitonic quantum nanostructures.

This paper is organized as follows: the theoretical framework is described in Section 2 along with numerical parameters considered for the study, the discussion of the results obtained is given in Section 3, and the conclusions are drawn in Section 4, followed by references.

2. Theoretical formalism
2.1. Excitonic states in a double quantum well

In this section, we provide the theoretical minimum for the understanding of physics involved with an interaction of our excitonic quantum mechanical system with the time-dependent periodic perturbation in the form of a laser field. The notation used is consistent throughout with conventional symbols and atomic units ( ) are used throughout the manuscript. We consider a coupled quantum well consisting of two GaAs quantum well layers and a thin AlxGa1−xAs barrier in the growth direction, considered along the z axis. We consider the conduction band electron effective mass to be position-dependent denoted by . The valence band consists of heavy-hole and light-hole subbands, and hole mass is described in terms of the Luttinger parameters of GaAs as: and , where and are Luttinger parameters and is the vacuum electron mass. The electron–hole reduced mass in x–y plane becomes . In the effective mass approximation, the Hamiltonian of the EQW can be written as

where is the z-direction Hamiltonian for the electron (hole). describes the relative motion of electron and hole in the plane perpendicular to the growth z axis.

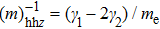
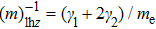
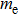
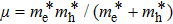
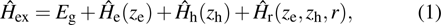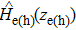
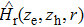
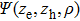
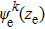
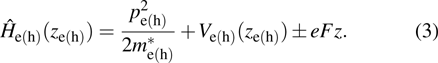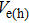
We assume the total EQW wavefunction is of the form , which can be expanded into a finite set of wave functions

where and describe the set of Coulomb-uncorrelated single particle electron and hole states in the coupled quantum well determined by the Schrödinger equation in the presence of static electric field applied along the growth z direction in coupled quantum wells
Here, ze and zh are the electron and hole coordinates in the growth z direction, respectively, F represents the static electric field, and is the electron (hole) rectangular confinement potential considered to be of the form

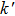
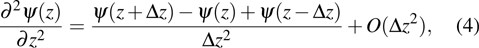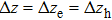
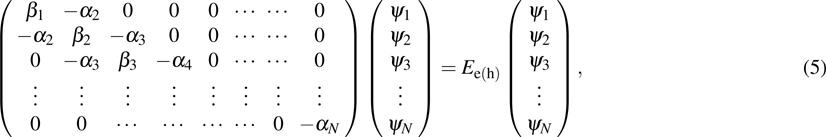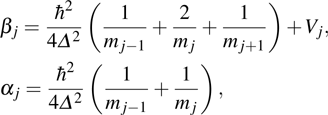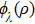
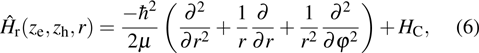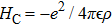
The index k ( ) refers to the quantum state of an electron (hole) in the conduction band (valence band). The allied index λ figures all basis states and runs onto the indices of electron and hole quantized states: ne electron states and nh hole states give a total of basis states. These states can be obtained by using the numerical finite difference method to obtain the uncorrelated electron or hole single particle states. The method has the advantage that it can be used even for complicated potentials and complicated boundary conditions and is used very often by engineers and physicists to solve partial differential equations which cannot be solved analytically. We use the central second-order finite difference formula based on Taylor series expansion, which consists of discretizing the electron and hole Hamiltonian on an equidistant spatial grid by approximating the partial derivatives as follows:

where corresponds to electron or hole single-particle wavefunction. The grid is taken to be one-dimensional with N+2 points and the grid steps over each variable have been taken to be the same, i.e., . Equation (3) gets reduced to a set of algebraic equations each for electron and hole which can be written in the form of a matrix equation
where
assuming that the wave function satisfies the boundaries of the quantum structure. The Hamiltonian for electron and hole is reduced to a tridiagonal matrix which is diagonalized numerically to obtain the electron and hole single-particle states wave functions. Further, in Eq. (2), denotes the in-plane components of the total wave function which can be solved employing finite difference method by writing the relative term of the total Hamiltonian in cylindrical coordinates
where is the negative Coulomb interaction term between carriers screened by the background dielectric constant and , r and φ are the polar coordinates of electron–hole relative motion, where is the relative electron–hole distance. The methodology can be applied to obtain the in-plane components of the wave function, , and the exciton transition energies achieved on a finite grid in the area , where R is the exciton confinement length taken to be 200 nm. The total wavefunction for EQW can be determined using Eq. (2).

Next, we study the interaction of our EQW system with a periodic field in the form of a monochromatic laser using Floquet quasienergy formalism. We discuss how the quasi-energy-state eigenvalues and eigenvectors may be determined through the solution of a stationary matrix eigenproblem, a method first introduced by Shirley[30] for a two-level quantum system in a periodic field. The theory has proved to be quite useful in studying the evolution of bound states with the periodic laser field. We consider the interaction of our EQW with a monochromatic linearly polarized periodic laser field along the z-axis and transition dipole moments are taken to be aligned with the polarisation direction. The Schrödinger equation for the interaction can be written as

where
is the electric field amplitude, and is the pulse shape of the periodic laser field considered to be sinusoidal with frequency ω. The unperturbed Hamiltonian has a complete set of orthonormal eigenfunctions
such that .

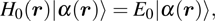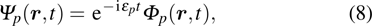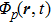
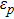
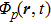
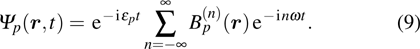According to the Floquet theorem, the wave function , called the quasienergy-state, can be written in the following form:

where is called the Floquet wave function periodic in time and is the Floquet characteristic exponent or the quasienergy. Expanding in a Fourier series, we can obtain

Therefore, a quasienergy state can be considered as a superposition of stationary states with energies equal to . The function can be further expanded in terms of an orthonormal set of unperturbed eigenfunctions , so that

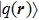
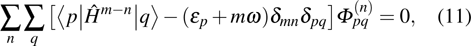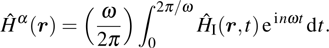Substituting Eqs. (9) and (10) into Eq. (7), we obtain the following system of coupled equations:

where

The above set of coupled equations can be recalibrated into an eigenvalue matrix equation

where is called the time-independent Floquet Hamiltonian. We use the nomenclature: , where the index α represents a quantum well excitonic state and the index n represents a Fourier component, ( ), such that . The matrix elements are given by . The quasienergies are eigenvalues of the secular equation det . The Floquet Hamiltonian acquires a block tridiagonal form. The quasienergies and quasienergy state can be determined by the solution of a time-independent Floquet matrix eigenproblem. has a periodic structure with only the number of ωʼs in the diagonal elements varying from one photon block to other blocks. This structure owns the quasienergy eigenvalues and eigenvectors of Floquet Hamiltonian with the periodic properties: and .

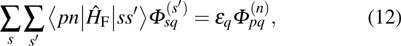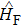
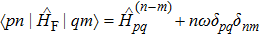
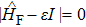
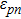
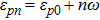
The probability of the occurrence of a transition between two quantum states, which is important for understanding many aspects of laser behavior, is given by

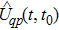
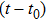
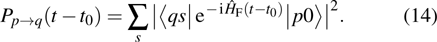where is the time evolution operator that gives the amplitude that a system in the initial state at the time t0 evolves to the final state in time according to the time-independent Floquet Hamiltonian . The experimental interest, however, is the transition probability which is averaged over initial times t0 and keeping the elapsed time fixed. This gives
Finally, averaging over, one obtains the long-time average transition probability

The method has advantages which include the removal of rapidly varying optical frequency from the time-dependent interaction Hamiltonian by transforming it into a time-independent Floquet Hamiltonian which can be easily diagonalized using standard coding in various scientific software including Fortran and Matlab, which are quite simple and accurate. We obtain the eigenvectors which are the dressed states or the adiabatic Floquet states of our quantum system and the eigenvalues are the quasienergies. Various nonlinear effects such as power broadening, dynamical Stark effect, etc., can be interpreted using the avoided crossing patterns in the quasi-energy diagram. The slow variation of amplitude and strength of laser field, multiphoton transitions between various levels, the shift of various states, etc., can be incorporated easily using this dressed picture representation which cannot be visualized using even the lowest-order perturbation theory.

2.2. Numerical parameters and computation

The material parameters considered in this study are in accordance with the reference.[36] The coupled quantum well under consideration consists of two GaAs wells with the right well width (RWW) of 8 nm. The AlGaAs barrier width (BW) is taken to be 2 nm. The aluminium concentration (x) is kept constant at 0.33. We define the skewness parameter (SP) as the ratio of right well width to left well width (LWW). 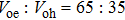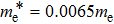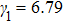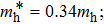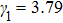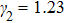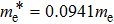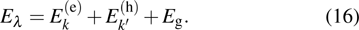The background dielectric constant is , and the energy-band offset ratio . The bandgap discontinuity at the GaAs/AlxGa1−xAs interface is linearly approximated as eV. The GaAs electron effective mass is taken to be and the Kohn–Luttinger parameters for pure GaAs are: and , giving the hole effective mass to be and for AlAs, the electron effective mass is taken to be and , , giving . The AlxGa1−xAs alloy parameters are linearly interpolated between those of GaAs and AlAs, thus giving and for the barrier region. We take the in-plane reduced mass to be . We use the numerical finite difference method to obtain the states of the EQW system as explained in Section 2. The energy levels of the coupled quantum well excitonic system thus obtained are given by

The single-particle states and the corresponding wavefunctions are shown for the two cases of the static electric field: F = 0 and F = 10 kV/cm in Fig. 1. In the present study, we consider the four quantum states ( –4) labelled as: (k = 1; GS state), (k = 1; EX1 state), (k = 2; EX2 state), and (k = 2; EX3 state), where + and — denote the parity of electron or hole states and hence, N = 4. On reviewing the symmetry of states under the inversion of coordinate axes along the growth z direction, it is observed that GS and EX3 states are symmetric while EX1 and EX2 states are antisymmetric. At F = 0 kV/cm, in a symmetric quantum well, the electrons and holes can tunnel through the barriers and direct exciton states can be formed as all levels are flat-banded. The pair states EX1 and EX2, formed with electron and hole in the same quantum well have close proximity and are electrically neutral. These form states in which radiative recombination takes place without phonon participation. In contrast, GS and EX3 that have a large spatial separation between electron and hole and have nonzero dipole moment are called indirect exciton states. The involvement of an impurity center, phonon, or another exciton is required for the radiative recombination of electron and hole in the formation of the indirect exciton. As the static electric field is increased, the symmetricity of the wave functions diminishes and they get localized in either of the quantum wells, as shown in the second panel of Fig. 1. Thus, a crossover of the exciton state occurs from direct to indirect type as the electric field grows. The result has been verified by previous researchers both theoretically[37] as well as experimentally.[38]

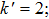
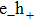
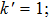
Fig. 1. The wavefunctions and the well potential for F = 0 kV/cm and F = 10 kV/cm for SP = 1.0 and BW = 40nm.

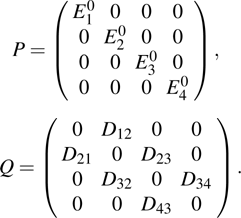To study the evolution of EQW states with a periodic laser, the Floquet theory is implemented to obtain the Floquet time-independent Hamiltonian in the form of the infinite matrix HF, as discussed in Section 2. The Floquet Hamiltonian thus obtained is shown below

where

The Floquet Hamiltonian is an infinite tridiagonal matrix with a periodic structure featuring only terms in the diagonal elements in various photon blocks. The structure endows the dressed quasienergy eigenvalues and eigenvectors of HF with periodic properties. The Floquet matrix includes the interaction of the quantum system with the periodic laser field in the off-diagonal terms of matrix type Q featuring elements

where are the corresponding transition dipole matrix elements between states i and j. The Eʼs in the Floquet matrix are the zero laser and static electric field energy values of various states of our system. We obtain the quasienergies and the corresponding Floquet states by diagonalizing the Floquet Hamiltonian in Eq. (17). The infinite matrix eigenvalue equation has to be truncated in these calculations. It is observed that the results converge after truncating HF to only a few photon blocks. Thus, using the Floquet Hamiltonian representation of a time-dependent Hamiltonian to a time-independent infinite matrix, we can easily calculate the dressed states and transition probabilities which are important parameters for the study in the laser physics and astrophysics.

3. Results and discussion

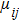
We considered the interaction of a single-mode sinusoidal periodic laser field with the exciton states of coupled GaAs/AlxGa1−xAs coupled double quantum well with a rectangular confinement potential. We apply the electric dipole approximation for the carrier–radiation interaction. The corresponding electron wave functions and quasienergies are obtained by the Floquet formalism. The analysis of our numerical results is as follows.

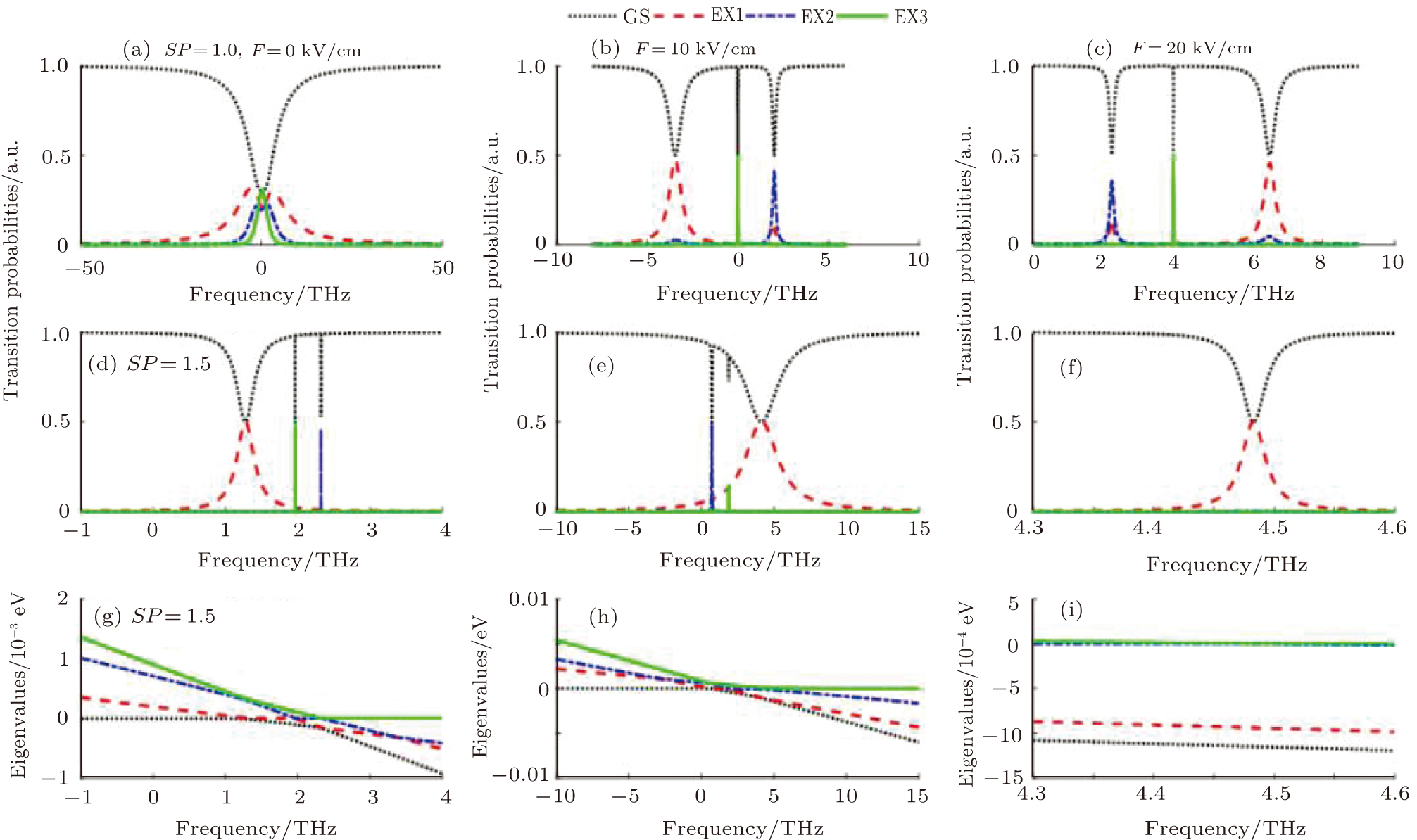
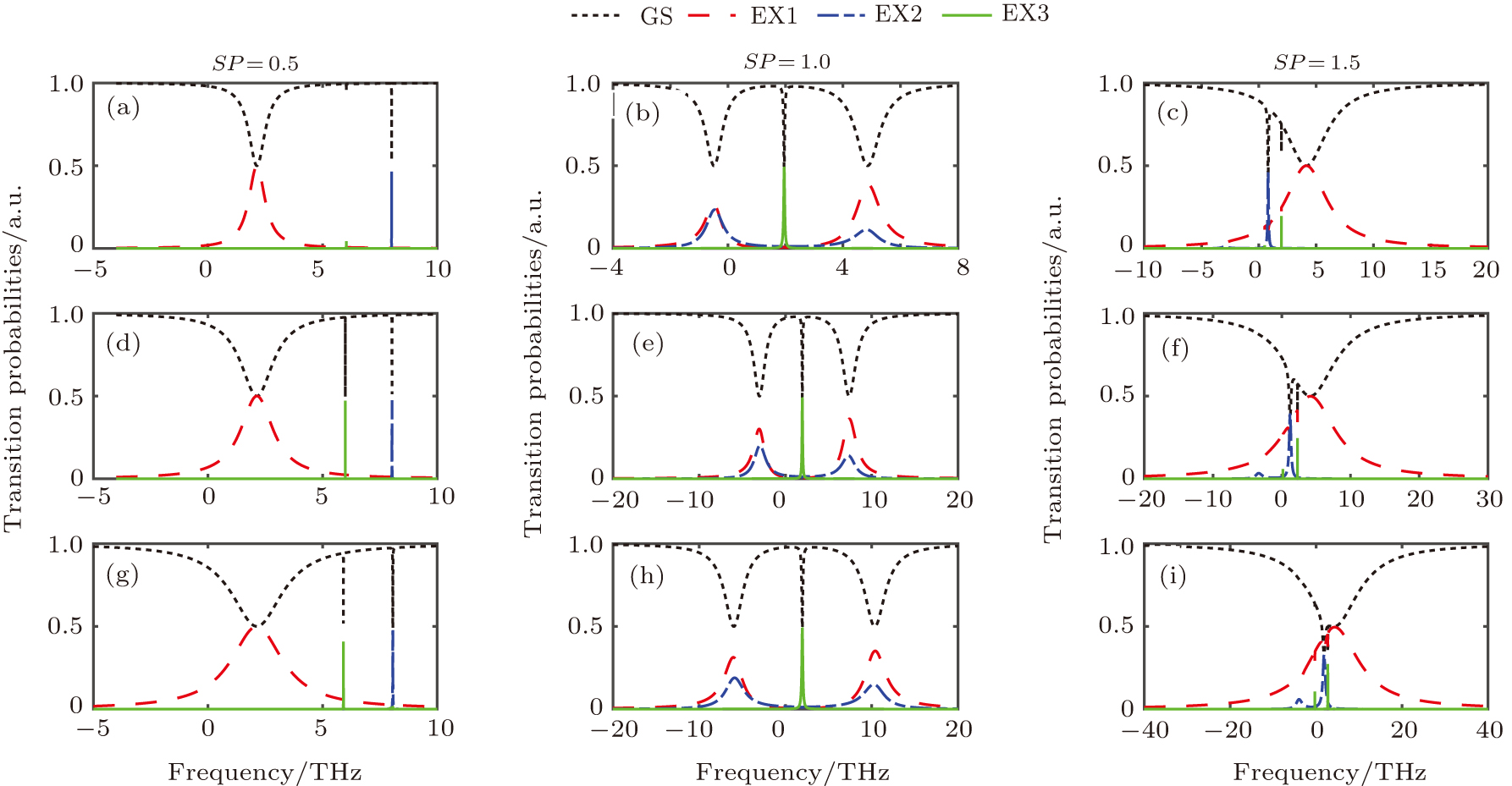
In Fig. 2, we show the computational results of transition probabilities for various transitions from the ground state and considered excited states of EQW with the frequency of the single-mode laser field. The results are plotted for different static field strengths and SP values indicated in the figure, keeping the LWW and BW fixed at 8 nm and 2 nm. The GS curves in the sub-figures of Fig. 2 show the ground state occupation probability (i.e., state character of ground state) and the other curves in the sub-figures show the probability of occupation or character composition of other excited states after the interaction with ground state takes place on the application of the laser. Initially, the system is prepared in the ground state. With the application of the laser, the transitions between the states get initiated. The crossover from direct to indirect exciton states may be observed as resonances in the transition spectra. The states are resonantly coupled with the laser field when the field frequency is close to the energy separation between the excitonic states. The transitions between the states occur whenever there are peaks in the probability curves. The transitions correspond to one-photon, two-photon, and three-photon for the transition from the ground state to first, second, and third excited state, respectively. The resonance between levels produces complete equilibration of the population. The strength of transition is indicated by the width of the resonance curve and not by the magnitude of the peak position of the curve. The multiphoton transitions discussed above depend heavily on the strength of the static electric field F. In the symmetric well case, the impact can be seen in Figs. 2(a) and 2(b), and the multiphoton transitions get augmented as the strength of electric field increases from 0 kV/cm to 10 kV/cm. There are secondary weak transitions which are not considered to be resonances. Further, with the increase of the static field strength, the interlevel transitions show a blue shift. For the asymmetric coupled wells, with the increase of the static field strength, the transition probabilities between the various states cease to exist gradually as observed in Fig. 2(f). This can be explained by the fact that the potential gets lowered due to an increasing electric field so that an electron (hole) eludes from the well towards left (right) and becomes free for higher electric field values. Thus, it becomes unavailable for transitions inside quantum wells. Thus, all high-field transitions involve the recombination of a hole and an electron localized on the same well.

Fig. 2. Variation of long-time averaged transition probabilities and quasienergies with the frequency of the laser field for different static electric field strengths and SP values. Panels (a)–(c) are plotted with SP = 1 and panels (d)–(i) are plotted for SP = 1.5. The laser intensity is kept constant at 2 W/cm2.

In Figs. 2(g)–2(i), we investigate the impact of the periodicity of the laser field on quasienergies of dressed states obtained using Floquet formalism. The sub figures show the shift in energies of the dressed states with the frequency of the laser. This indicates how states change their character composition as laser intensity increases. In Fig. 2(g), at the frequency of 1.278 THz, the dressed indirect exciton state GS picks up the character of dressed direct exciton state EX1 and the level repulsion occurs. This interaction drives the ground state to lower energies and levels diverge from each other. Further increase in the frequency again mixes the character of direct and indirect exciton states GS and EX1 at the frequency of 1.966 THz and GS and EX2 at the frequency of 2.322 THz. These positions represent the position of transitions from one level to another. Further, the minimum separation between the branches of two quasienergies is correlated with the width of the resonance peak at its associated avoided crossing and the placement of minimum separation determines the positions where states divert from their character composition and resonance occurs. In Fig. 2(i), the levels almost level off due to the non-interaction between levels at high field values. The strong coupling between excitonic dressed states on the introduction of a laser has a potential application in developing the optical sensors that may be used to detect the THz radiation. Attributing to their possible applications as sensors, substantial attention to these structures can be foreseen.

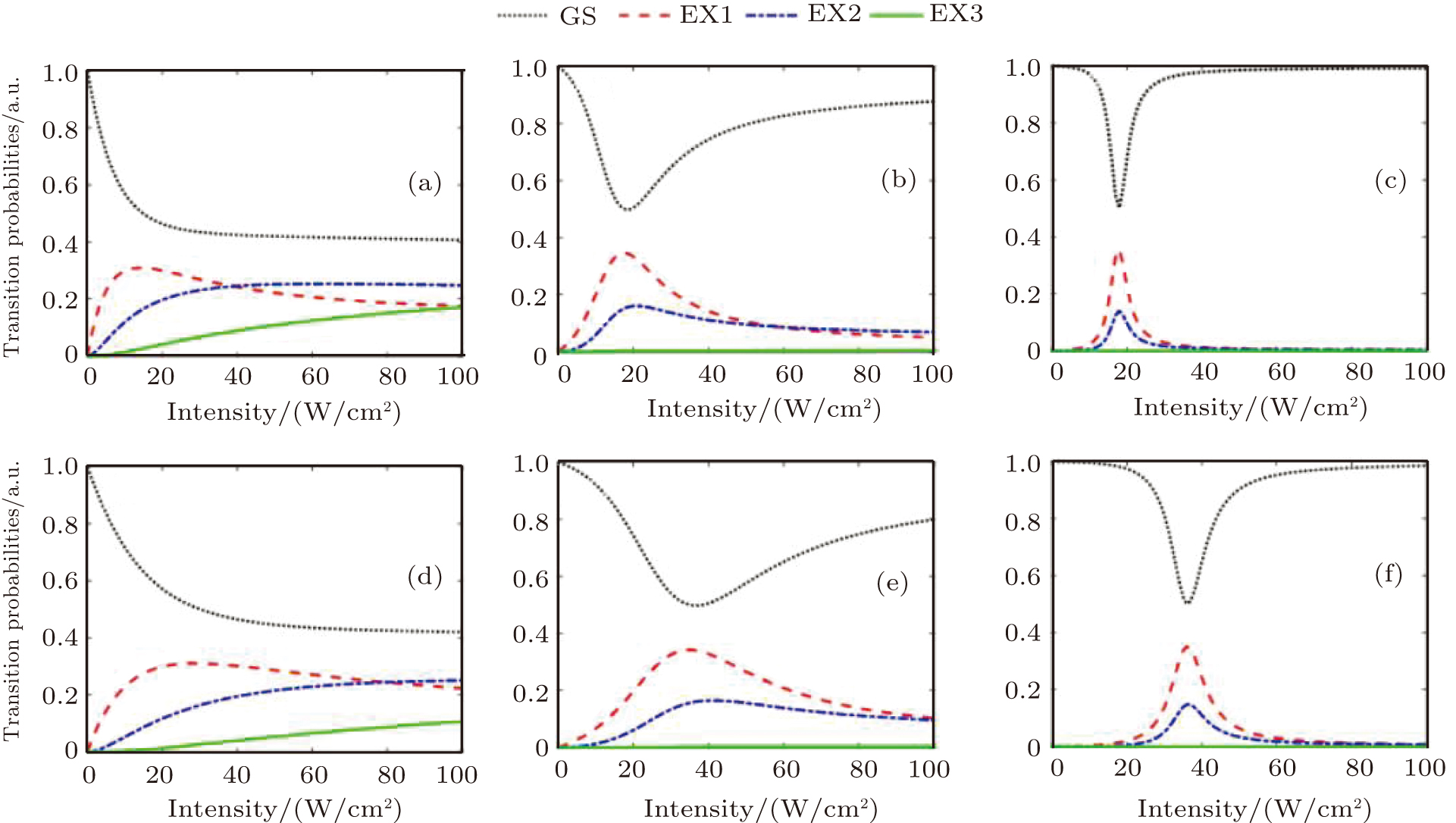
Modern spectroscopy relies largely on high power lasers. The commencement of non-perturbative effects with radiation intensity can be seen in Fig. 3. It is observed that the onset of laser excitation power or equivalently electric field strength leads to broadening of linewidth. The central part of the probability curve gets flattened for high excitation intensities as shown in Figs. 3(a), 3(d), and 3(g) for SP = 0.5 when laser intensity is 5 W/cm2. This may be attributed to the higher pumping rate that results in more absorption rate than the relaxation rate, causing a decrease of population in absorbing levels that leads to saturation of population densities. This effect is known as power broadening. The saturation absorption occurs for EX1 and EX2 states at the resonance position, i.e., at the center of a transition peak that leads to sideways shifting of photon absorption as observed for the symmetric well in Figs. 3(b), 3(e), and 3(h). Also, the increase of electric field modification in energy-levels occurs, which leads to blue-shift of the transition line in the symmetric well case. A further increase in SP to 1.5 leads to cleavage of transition profiles of dressed EX1 and EX2 states as seen in Figs. 3(c), 3(f), and 3(i). This occurs due to the localization of hole wavefunctions to the right well for SP = 1.5, whereas for low SP values, electron and hole wavefunctions are coupled together since they are either localized on the same well or partially localized on both wells, the effect that has been observed by Mcllroy.[39] This leads to a decrease in dipole matrix element values for the considered transitions and hence no significant changes are observed on the increase in the intensity of the laser field for higher SP values.

Fig. 3. Variation of transition probabilities with the frequency of the laser field for different laser intensities and SP values. The laser intensity is: (a)–(c) 5 W/cm2, (d)–(f) 20 W/cm2, and (g)–(i) 50 W/cm2. Static electric field strength is taken as 10 kV/cm.

In Fig. 4, we show the variation of quasienergies with laser intensity for different static field strengths, as indicated in the figure. ω is taken to be 4 THz. At zero static field strength, quasienergies are a nonlinear function of laser field intensity but are almost linear for high laser intensities. As the dc field strength is increased from 0 kV/cm to 20 kV/cm, significant intermixing of bare states is observed with the increase of laser intensity. At higher field strength of 55 kV/cm as in Fig. 4(c), the quasienergy associated with the unperturbed excited state EX2 exhibits a shift and undergoes an avoided crossing with the quasienergy associated with excited state EX3, which further undergoes an avoided crossing with dressed GS state. The shifts of the quasienergies against the unperturbed energy eigenvalues as the driving amplitude increases are generally known as ac-Stark shifts, the effect that has been observed in various atomic and heterostructure systems.[40,41]

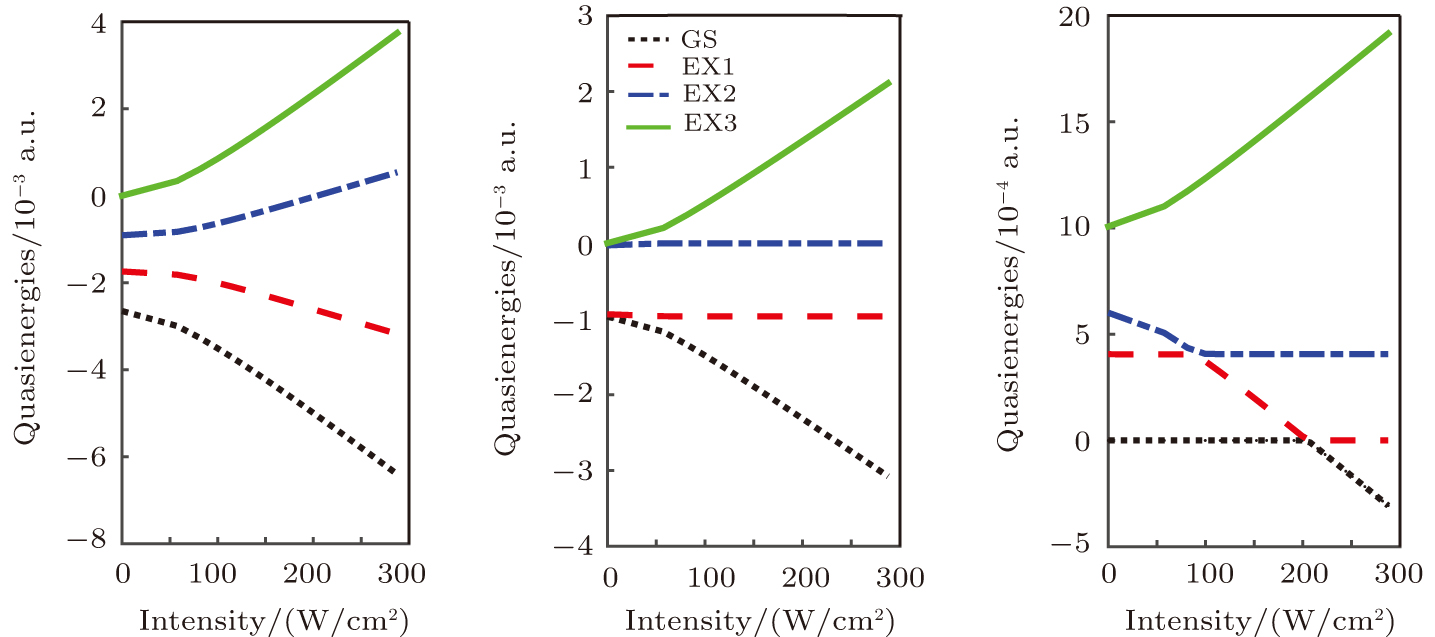Fig. 4. Dressed states quasienergies as a function of the laser field intensity for different static field strengths: F = 0, 20, and 55 kV/cm.

In Fig. 5, we show the variation of transition probabilities with the laser field intensity for different barriers widths while keeping well-widths constant at 8 nm. It is observed that the smaller the barrier width, the stronger the interaction between the levels for all laser intensities, as the values of transition probabilities have definite non-zero values for all intensities. As the barrier width increases from 20 nm to 60 nm, the transitions get localized to a limited intensity range from 0 W/cm2 to 50 W/cm2. Also, with the enhancement of laser frequency, the curves show broadening and shift in the resonance positions. The results may provide insight into devising of laser devices suited for the particular frequency ranges.

Fig. 5. Transition probabilities of various states with the laser field intensity for different barrier widths. In panels (a)–(c), ω = 6 THz and in panels (d)–(f), ω = 8 THz, while SP = 1.0 and F = 5 kV/cm in all the panels.
4. Conclusion

In conclusion, in the preceding study, we have investigated the interaction of EQW with a strong, periodic THz laser field, and static electric field. The numerical technique employed to obtain the unperturbed states of EQW system is employed in this work, which is the well-constructed central second-order finite difference. The interaction with the laser field is described with a nonperturbative Floquet approach, providing a time-dependent solution of the Schrödinger equation. We obtain analytical expressions for the variation of the quasienergies and Floquet states as functions of the field parameters. Many nonlinear effects are observed including the avoided crossing of dressed states, power broadening, and ac-Stark shift. The study can provide a strong impetus for the development of novel optoelectronic devices such as electro–optical modulators, photodetectors, sensors, and quantum switches.

Reference
[1] Dhillon S S Vitiello M S Linfield E H et al. 2017 J. Phys. D: Appl. Phys. 50 043001 https://dx.doi.org/10.1088/1361-6463/50/4/043001
[2] Xiang D Stupakov G 2009 Phys. Rev. Spec. Top Accel. Beams 12 080701 https://dx.doi.org/10.1103/PhysRevSTAB.12.080701
[3] Dunning M Hast C Hemsing E Jobe K McCormick D Nelson J Raubenheimer T O Soong K Szalata Z Walz D Weathersby S Xiang D 2012 Phys. Rev. Lett. 109 074801 https://dx.doi.org/10.1103/PhysRevLett.109.074801
[4] Köhler R Tredicucci A Beltram F Beere H E Linfield E H Davies A G Ritchie D A Iotti R C Rossi F 2002 Nature 417 156 https://dx.doi.org/10.1038/417156a
[5] Stojanovic N Drescher M 2013 J. Phys. B: At. Mol. Opt. Phys. 46 192001 https://dx.doi.org/10.1088/0953-4075/46/19/192001
[6] Ajito K 2015 IEEE Trans. Terahertz Sci. Technol. 5 1140
[7] Taslakov M Simeonov V van den Bergh H 2008 J. Phys.: Conf. Ser. 113 012055 https://dx.doi.org/10.1088/1742-6596/113/1/012055
[8] Kemp M C Taday P F Cole B E Cluff J A Fitzgerald A J Tribe W A R 2003 Proc. SPIE Int. Soc. Opt. Eng. 5070 44
[9] Davies A G Burnett A D Fan W Linfield E H Cunningham J E 2008 Materials Today 11 18 https://dx.doi.org/10.1016/S1369-7021(08)70117-2
[10] Sudradjat F F Zhang W Woodward J Durmaz H Moustakas T D Paiella R 2012 Appl. Phys. Lett. 100 241113 https://dx.doi.org/10.1063/1.4729470
[11] LiKamWa P Miller A Park C B 1990 Appl. Phys. Lett. 57 1846 https://dx.doi.org/10.1063/1.104035
[12] Maslov A V Citrin D S 2003 J. Appl. Phys. 93 10131 https://dx.doi.org/10.1063/1.1574590
[13] Yang R Q Pei S S 1995 Superlatt. Microstruc. 17 77 https://dx.doi.org/10.1006/spmi.1995.1017
[14] Liu G Guo K Hassanabadi H Lu L 2012 Physica B 407 3676 https://dx.doi.org/10.1016/j.physb.2012.05.049
[15] Gambhir M Prasad V 2018 Revista Mexicana de F?sica 64 439 https://dx.doi.org/10.31349/RevMexFis.64.439
[16] Hassanabadi H Rahimov H Zarrinkamar S 2012 Few-Body Syst. 52 87 https://dx.doi.org/10.1007/s00601-011-0234-9
[17] Sargolzaeipor S Hassanabadi H Chung W S 2019 Mod. Phys. Lett. A 34 1950023 https://doi.org/10.1142/S0217732319500238
[18] Onyeaju M C Idiodi J O A Ikot A N Solaimani M Hassanabadi H 2017 J. Opt. 46 254 https://dx.doi.org/10.1007/s12596-016-0359-9
[19] Lua L Xie W Hassanabadi H 2011 J. Lumin. 131 2538 https://dx.doi.org/10.1016/j.jlumin.2011.06.051
[20] Wagner M Schneider H Stehr D Winnerl S Andrews A M Schartner S Strasser G Helm M 2010 Phys. Rev. Lett. 105 167401 https://dx.doi.org/10.1103/PhysRevLett.105.167401
[21] Galbraith I Chari R Pellegrini S Phillips P J Dent C J van der Meer A F G Clarke D G Kar A K Buller G S Pidgeon C R Murdin B N Allam J Strasser G 2005 Phys. Rev. B 71 073302 https://dx.doi.org/10.1103/PhysRevB.71.073302
[22] Rice W D Kono J Zybell S Winner S Bhattacharyya J Schneider H Helm M Ewers B Chernikov A Koch M Chatterjee S Khitrova G Gibbs H M Schneebeli L Breddermann B Kira M Koch S W 2013 Phys. Rev. Lett. 110 137404 https://dx.doi.org/10.1103/PhysRevLett.110.137404
[23] Su M Y Carter S G Sherwin M S 2002 Appl. Phys. Lett. 81 1564 https://dx.doi.org/10.1063/1.1502441
[24] Faisal F H M 1987 Theory of Multiphoton Processes New York Plenum Press
[25] Shore B W 1990 The Theory of Coherent Atomic Excitation New York Wiley
[26] Shirley J H 1965 Phys. Rev. B 138 979 https://dx.doi.org/10.1103/PhysRev.138.B979
[27] Lumb S Prasad V 2013 J. Mod. Phys. 4 1139 https://dx.doi.org/10.4236/jmp.2013.48153
[28] Rodríguez A H Montes L M Giner C T Ulloa S E 2005 Phys. Status Solidi B 242 1820 https://dx.doi.org/10.1002/(ISSN)1521-3951
[29] Lahon S Gambhir M Jha P K Mohan M 2010 Phys. Status Solidi B 247 962 https://doi.org/10.1002/pssb.201046027
[30] Duan S Zhang W Xie W Ma Y Chu W 2009 New J. Phys. 11 013037 https://dx.doi.org/10.1088/1367-2630/11/1/013037
[31] Brandes T Aguado R Platero G 2004 Phys. Rev. B 69 205326 https://dx.doi.org/10.1103/PhysRevB.69.205326
[32] Johnsen K Jauho A P 1999 Phys. Rev. Lett. 83 1207 https://dx.doi.org/10.1103/PhysRevLett.83.1207
[33] Villavicencio J Maldonado I Cota E Platero G 2011 New J. Phys. 13 023032 https://dx.doi.org/10.1088/1367-2630/13/2/023032
[34] Sentef M A Claassen M Kemper A F Moritz B Oka T Freericks J K Devereaux T P 2015 Nat. Commun. 6 7047 https://dx.doi.org/10.1038/ncomms8047
[35] Giovannini U D Hübener H Rubio A 2016 Nano Lett. 16 7993 https://dx.doi.org/10.1021/acs.nanolett.6b04419
[36] Wilkes J Muljarov E A 2016 New J. Phys. 18 023032 https://dx.doi.org/10.1088/1367-2630/18/2/023032
[37] Szymanska M H Littlewood P B 2003 Phys. Rev. B 67 193305 https://dx.doi.org/10.1103/PhysRevB.67.193305
[38] Butov L V Zrenner A Abstreiter G Petinova A V Eberl K 1995 Phys. Rev. B 52 12153 https://dx.doi.org/10.1103/PhysRevB.52.12153
[39] McIlroy P W A 1986 J. Appl. Phys. 59 3532 https://dx.doi.org/10.1063/1.336772
[40] Vela-Arevalo L V Fox R F 2004 Phys. Rev. A 69 063409 https://dx.doi.org/10.1103/PhysRevA.69.063409
[41] Gudwani M Prasad V Jha P K Mohan M 2008 Int. J. Nanosci. 7 215 https://dx.doi.org/10.1142/S0219581X08005353