† Corresponding author. E-mail:
In this paper, the giant magnetoresistance (GMR) multilayer sensor is fabricated with a Wheatstone bridge, and it exhibits excellent performance with a sensitivity of 2.8349 mV/(V/Oe) (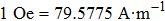
Since its discovery in 1988, the giant magnetoresistance (GMR) effect has been widely studied from both academic and technological viewpoint[1–13] because of its advantages such as high sensitivity, large magnetoresistance ratio, and good compatibility with standard integrated circuit processes. The GMR sensor was first industrialized by NVE in 1994 and has been well used in medical and industrial circles, automotive electronics, etc.[14–19] As a type of magnetic sensing device, the GMR sensor can be used as an angular transducer in the electronic compass, a pedal position detector in vehicles, and an angle encoder in industrial controls[20–25] to replace the Hall-effect device and anisotropic magnetoresistance (AMR) sensor.[26,27] The angular dependence of Hall-effect device, AMR sensor and GMR spin-valve sensor have been thoroughly investigated in recent years.[7,28–32] The angular dependence of the GMR multilayer film has been reported.[33–38] This dependence was introduced via the angular variation of transmission and reflection coefficient in Fuchs–Sondheimer boundary conditions.[34,39] The angular dependence of the GMR multilayer film has been systematically and theoretically studied in depth by Vedyayev et al..[39] They presented an analytical quantum-statistical theory of the angular variation of the GMR in magnetic multilayers, in which both the spin-dependent scattering of conduction electrons and the spin-dependent potential barriers between successive layers are taken into account.[20] However, the angular dependence of the GMR sensor based on the GMR multilayer film was rarely reported.[40,41] It is found that the GMR sensor is sensitive to angular variation and can be described with a cosine function.
In this paper, the output characteristics of the sensor are further analyzed, and the angular dependence of the GMR multilayer sensor is studied. First, the magnetic field direction, which is at an angle with respect to the sensitivity axis, is changed. The sensitivity of the GMR multilayer sensor is studied. Second, a series of rotating magnetic fixed fields is applied at different directions from 0° to 360°. Most importantly, a model is proposed to further describe the output characteristics of the GMR multilayer sensor. This model has not been reported in other papers. It differs from that in the work by Zhu,[43] where only a series of rotating magnetic fixed fields is used, and a simple modified model is proposed to describe the output characteristics of the GMR multilayer sensor.
In this work, the GMR multilayer films were deposited on Si/SiO2 (

Figure
Two test systems were employed in this work. In the measurement of the low magnetic field range, a Helmholtz coil was used to produce the magnetic fields in a range from −50 Oe to +50 Oe. The Helmholtz coil system consists of a two-dimensional (2D) Helmholtz coil and a device fixture. In the measurement, the sensor under test was fixed on the device fixture, and the sensor transfer curve was obtained by sweeping the magnetic fields by changing the current in the Helmholtz coil. The current source for the Helmholtz coil is controlled by a computer, which adjusts the sweeping range and controls the direction of the magnetic fields. The angle between the direction of the magnetic field and the sensitive axis of the sensor is denoted as θ, as shown in Fig.
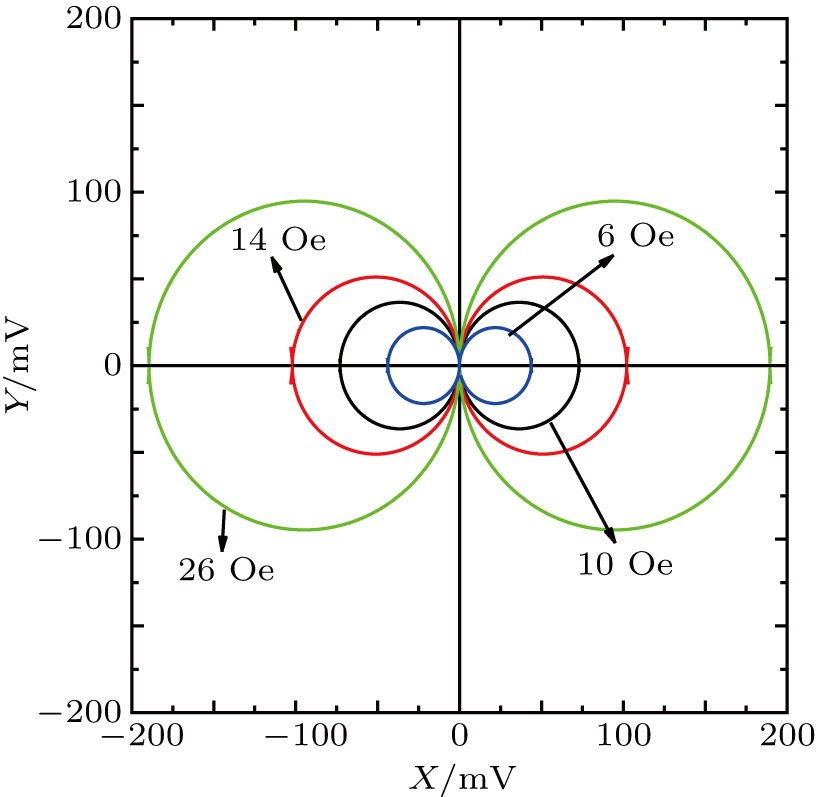
In this work, first, the transfer curves of the GMR sensor were acquired by sweeping the external magnetic field from −50 Oe to +50 Oe in steps of 0.25 Oe along the sensitive axis. Second, the transfer curves of the GMR sensor were recorded by sweeping the external magnetic field from −2000 Oe to +2000 Oe in steps of 50 Oe along the sensitive axis. Third, the transfer curves of the GMR sensor were acquired by sweeping the external magnetic field with different angles with respect to the sensitive axis, from −50 Oe to +50 Oe. Finally, the rotation transfer curves of the GMR multilayer sensor were acquired by a rotating field. The magnitudes of the fields were 6.0 Oe, 10.0 Oe, 14.0 Oe, and 26.0 Oe.
The transfer curves of the GMR sensor is shown in Fig.
The output voltage of the sensor remains steady in a range from 50 Oe to 750 Oe. When the magnetic field changes from 750 Oe to 1250 Oe, the output voltage decreases with external increasing magnetic field. Then, the output voltage maintains a steady value, which is identical to the field at 0 Oe, when the field is larger than 1250 Oe.
In the range of 26 Oe–750 Oe, a platform is shown in the transfer curve. The MR ratio of R1 to R3 is saturated, and R2 and R4 are shielded. Thus, in the range of 750 Oe–1250 Oe, the imbalance of the Wheatstone bridge output is inversely proportional to the magnetic field because R1 and R3 maintain the steady minimum values, and the effect of the shielding layer on R2 and R4 gradually disappears. After the final phase, the output voltage remains at the steady minimum values with the increase in magnetic field because R2 and R4 decrease to a minimum value, and the MR ratio of R1 to R3 remains saturated.
The transfer curves of the GMR sensor are shown in Fig.
 | Fig. 6. Rotation transfer curves of sensor at different rotating fields: 6 Oe, 10 Oe, 14 Oe, and 26 Oe. |
As shown in Fig.
The theoretical angular characteristic of the GMR sensor with the Wheatstone bridge structure is described as
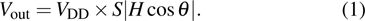 |
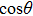
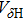
As shown in Fig.
Considering the bridge offset Voffset and nonlinear error 
 |
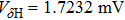
To analyze the output characteristics of the GMR sensor, a simple model (
Let 

 |
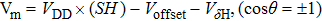
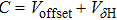
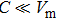
 |
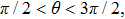
 |
 |
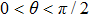
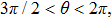
 |
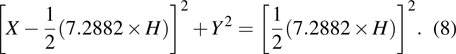 |
Equations (
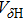

 | Fig. 7. Transfer curves of the sensor at different magnitudes of the rotating field: 6.0 Oe, 10.0 Oe, 14.0 Oe, and 26.0 Oe. |
The relationship between X and Y is simulated using MATLAB. The magnitudes of the rotating magnetic field are assumed to be 6.0 Oe, 10.0 Oe, 14.0 Oe, and 26.0 Oe. Figure
 | Fig. 8. Simulation results of relationship of X and Y at different magnitudes of rotating field: 6.0 Oe, 10.0 Oe, 14.0 Oe, and 26.0 Oe. |
Figure 
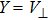
In this paper, the properties of the GMR multilayer sensor are analyzed and the angular dependence of the GMR sensor is characterized. The sensor exhibits excellent performance with a sensitivity of 2.8349 mV/(V/Oe) and a saturation field of 26 Oe along the sensitive axis. The GMR sensor in a high magnetic field is also characterized. The sensitivity decreases from 2.8349 mV/(V/Oe) at 0° to 0.0175 mV/(V/Oe) at 90°. Then, a model is proposed to describe the output characteristics of the GMR sensor. The equation consists of two exactly symmetrical circles in the saturation field of 26 Oe, and the experimental results are consistent with the simulation results. The advantage of this model is that it is simpler and more intuitive, and it can be applied to the research of two-dimensional sensors.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] |







