† Corresponding author. E-mail:
The exciton dynamics in a WS2 monolayer with strain are studied by transient absorption measurements. We measure the differential transmission signal from monolayer WS2 as a function of the probe wavelength at different levels of strain applied to the sample. The differential transmission spectrum has a positive maximum value at about 614 nm and shows no significant strain dependence. By time-resolving the differential transmission signal, we find that the strain has a minimal effect on the exciton formation process. However, the exciton lifetime is significantly reduced by strain. These results provide useful information for applications of WS2 in flexible electronic and optoelectronic devices where strain is inevitable.
Since graphene was successfully exfoliated in 2004,[1] it has attracted a lot of attention, owing to its excellent electronic properties that are attractive for many applications.[2,3] Due to the lack of a bandgap of graphene, which is desirable for logic electronics and optoelectronics, the interest in two-dimensional (2D) materials has expanded to other layered materials such as transition metal dichalcogenides (TMDs).[4–6] TMDs are layered materials with a formula of 
WS2 is one of the representative semiconducting TMDs, with a bandgap in the range of 1.3 eV–2.0 eV.[18,19] Bulk WS2 exhibits an indirect bandgap of 1.3 eV. With the number of layers decreasing, monolayer WS2 becomes a direct semiconductor with a bandgap of 2.0 eV.[20] Theoretical calculations predicted that WS2 has high charge mobility among the semiconducting TMDs due to the reduced effective mass.[21] The high photoluminescence (PL) yield of monolayer WS2 is attractive to applications in optoelectronic devices demanding high quantum efficiency.[22] With these excellent optical and electronic properties, WS2 is expected to be widely used in electronic and optoelectronic devices.[23–27]
The physical properties of TMDs depend on the band structure. As such, the strain can be used to modulate the band structure and thus tune the physical properties of TMDs.[28,29] Recently, the effect of strain in TMDs has been investigated extensively both theoretically and experimentally.[30–32] Theoretical calculations show that for TMD monolayers with 1T structures, such as HfS2 and HfSe2, the uniform isotropic strain in a range from −5% to 5% of their bandgap can increase, while for 2H TMDs the bandgap decreases linearly as the lattice constant increases.[33] When applying a uniaxial strain, the results are similar but have a smaller modulation of the bandgap.[34] Recent experiments indicated that the A-exciton exhibits a redshift under a rate of 46 meV/% strain for WS2.[35] The PL yield for bilayer WSe2 is improved dramatically under uniaxial strain, making it comparable to unstrained monolayer WSe2 due to an indirect-to-direct bandgap transition for strained bilayer WSe2.[36] TMD field-effect transistors (FETs) have been fabricated on flexible substrates and the effect of strain has been studied.[37,38]
Exciton dynamics in monolayer TMDs play an important role in determining their electronic and optical properties, and have been studied using transient absorption measurements.[39–43] However, the effect of strain on excitons dynamics has been less explored. In this paper, we report a transient absorption measurement of exciton dynamics in monolayer WS2 that is subjected to various levels of strain. These results provide useful information for application as TMDs in flexible electronic and optoelectronic devices are inevitably subjected to strain.
Monolayer WS2 samples were obtained by micromechanical exfoliation of bulk material on a thin polydimethylsiloxane (PDMS) flexible substrate. Their monolayer thickness was confirmed by using optical contrast and PL yield. The PL spectrum was measured using a confocal microscope system (LabRAM HR Evolution) with a 50 ×objective lens, and under the excitation of a 532-nm continuous-wave laser.
The exciton dynamics in monolayer WS2 samples were studied using a transient absorption technique. The differential transmission setup for the transient absorption measurements is shown in Fig. 


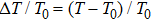
A two-point bending apparatus[36,44] was used to apply uniaxial tensile strain to the monolayer WS2 flakes as shown in Fig. 
The setup of the bending apparatus without strain and with different levels of strain in the transient absorption system are shown in Figs.
Figure
 | Fig. 2. (a) Optical microscope image of the WS2 sample. (b) Optical contrast of green channel along red dashed line in panel (a). (c) PL spectrum of monolayer WS2 sample without strain. |
We study the exciton dynamics in monolayer WS2 with different probe wavelengths and different levels of strain. Firstly, the monolayer WS2 sample and the PDMS film (with a size of 2 cm×2 cm and a thickness of 0.092 cm) are mounted on the central part of the PC substrate (with a length of 12 cm) as shown in Fig. 

Figure
Next, we use a 410-nm pump pulse with a peak fluence of 




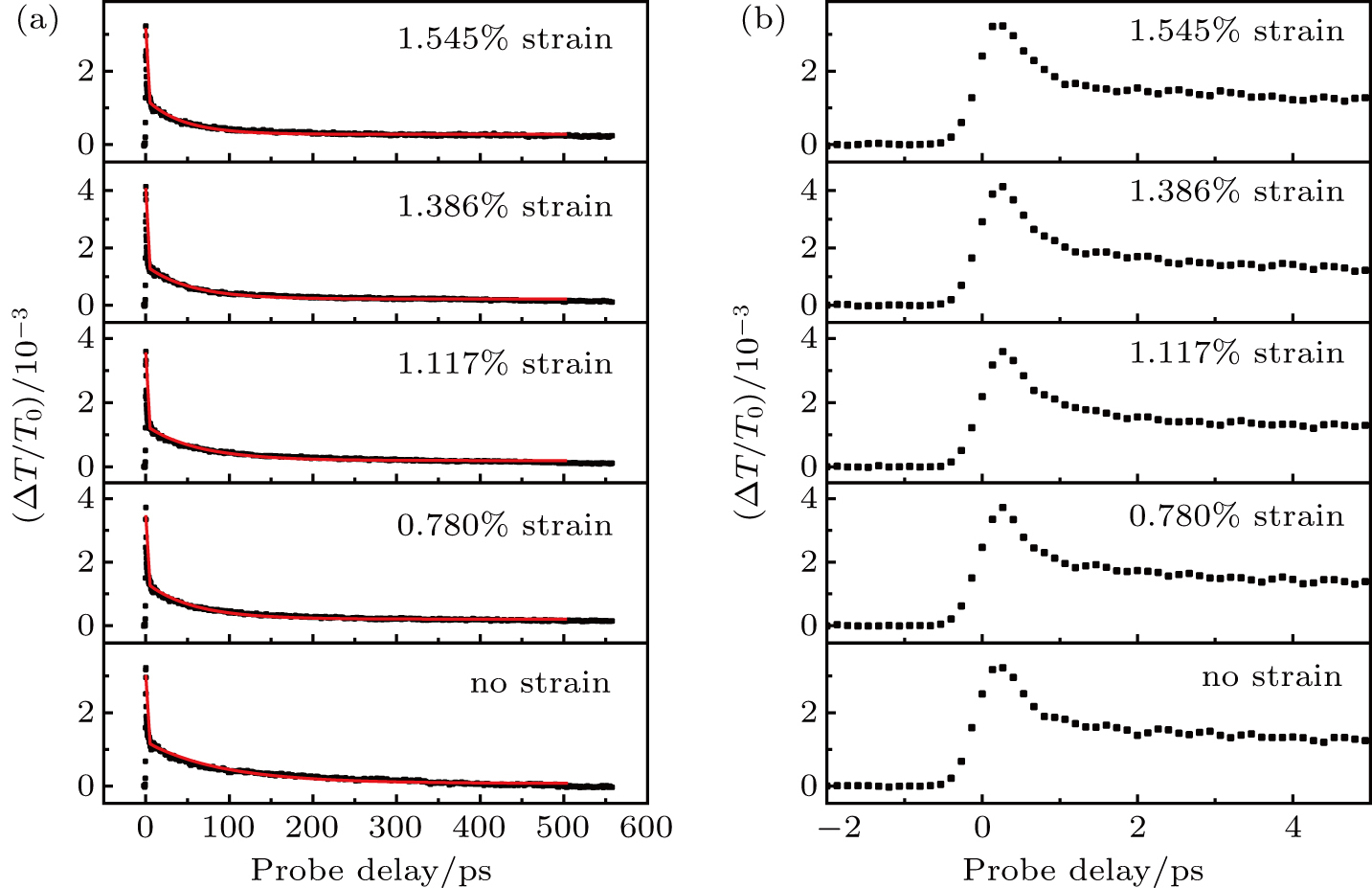
Previous studies have established that the short and long decay time are associated with the exciton formation and recombination process in TMD monolayers, respectively.[51,52] The 410-nm pump pulse injects free electron–hole pairs. Due to the enhanced Coulomb interaction with reduced dielectric screening in monolayer WS2, the electrons and holes form excitons rapidly. Since the free electron–hole pairs produce a stronger transient absorption than excitons of the same density, the signal decreases initially as reflected by 
In summary, we have performed transient absorption measurements of exciton dynamics in TMDs with strain. We measured differential transmission signals from monolayer WS2 as a function of the probe wavelength in cases with strain at different levels and without strain, respectively. At all the levels of strain studied, the peak differential transmission had a positive maximum value at about 614 nm, showing no significant strain dependence. By time-resolving the differential transmission signal, we found that the results suggest that the strain has a minimal effect on the exciton formation process; however, even a strain of about 1.5% reduces the exciton lifetime by a factor of about two. These results provide useful information for applications of TMDs in flexible electronic and optoelectronic devices.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 |