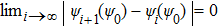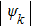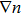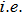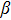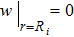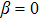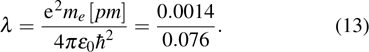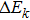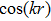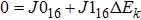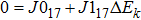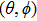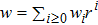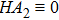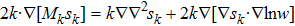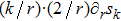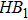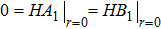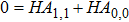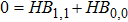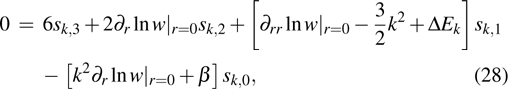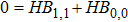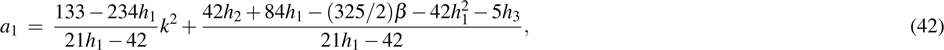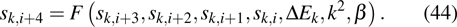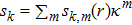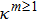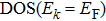2.1. Main ideaThe single-electron wavefunction in solids is identified by wavevector k. The HF equation of
 reads as
reads as
where the two real-valued functions
UL and
Uc satisfy the Poisson equations (
Ql and
Rl are the charge and the position of the
l-th ion) and the complex-valued function

reads as
where
w is defined as

. Here, because the summations over
q and over
k +
q are different expressions of the same object,
w is
k-independent. Besides the HF equation, each

also satisfies
where

is the volume of a cell,
a is the lattice constant,
VFS is the volume of the Fermi sphere, and

is the total ionic charge per cell. Moreover, the
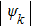
are orthogonal to each other.
In DFT,[10–16] the exchange–correlation energy
 is assumed to be in a simple functional of n and
is assumed to be in a simple functional of n and
 , where n is the total electronic density and then each HF equation, which is an integral–differential equation of
, where n is the total electronic density and then each HF equation, which is an integral–differential equation of
 , is approximated to be a differential one with the same order,
, is approximated to be a differential one with the same order,
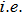 , a 2nd-order PDE. As previously mentioned, if the single-body wavefunction is described with a PDE, the PDE should be at least 3rd-order, rather than 2nd-order.
, a 2nd-order PDE. As previously mentioned, if the single-body wavefunction is described with a PDE, the PDE should be at least 3rd-order, rather than 2nd-order.
Actually, it is unnecessary to depend on those assumptions for
 . There exists a strict and straightforward method of solving the HF equations. By denoting
. There exists a strict and straightforward method of solving the HF equations. By denoting
 as
as
 , we can re-write each HF as
, we can re-write each HF as
where
Ek is space-independent and also time-independent. All terms in this form belong to one of two classes: one is
k-dependent and the other
k-independent. The condition for an equation in such a form having solutions at any
k-value is that all
k-independent terms in Eq. (
4) form a closed relation and the
k-dependent terms are governed by a few
k-independent terms,

where
E0 is the corresponding atomic level of those extended-states and **
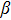
is a constant

. Equation (
5) is a 2nd-order linear PDE of
w, and its solution is determined by a physical boundary condition
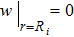
which means the density of valence electrons at the cation position is 0. Moreover, the linearity of Eq. (
5) can warrant

to be satisfied easily by multiplying the solution of Eq. (
5) by a constant.
Due to the (1/r)-dependent part of the operator
 in Eq. (5),
in Eq. (5),
 exists if
exists if
 . But the mathematical property of the isotropic part of UL, or the fact that
. But the mathematical property of the isotropic part of UL, or the fact that
 is a power series of
is a power series of
 , determines the expansion coefficients wi of
, determines the expansion coefficients wi of
 as 0 for all odd i in the case of
as 0 for all odd i in the case of
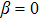 . This might be unable to warrant the physical boundary condition
. This might be unable to warrant the physical boundary condition
 to be fulfilled when
to be fulfilled when
 . In contrast, if
. In contrast, if
 , it is possible for
, it is possible for
 to appear, which is favorable for the fulfillment of the physical boundary condition.
to appear, which is favorable for the fulfillment of the physical boundary condition.
After knowing the profile of the total particle density
 from Eq. (5), each
from Eq. (5), each
 , or each “relative probability amplitude”
, or each “relative probability amplitude”
 , can be solved from Eq. (6). The real part and the imaginary part of Eq. (6) yield
, can be solved from Eq. (6). The real part and the imaginary part of Eq. (6) yield
where
Having obtained the expressions of
VS and
VC in terms of
sk and
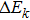
from Eqs. (
7) and (
8), we can substitute them into Eqs. (
9) and (
10) and have
Comparing the

-dependent terms, as well as the
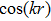
-dependent terms, in Eqs. (
14) and (
15), we obtain 4 equations respectively for their

-dependent terms and

-dependent terms. The four equations are in fact 2 pairs and in each pair the two equations are the same because one is merely the other multiplied by a constant. Thus, we obtain two equations:
Here, we utilize the formulas
Note that equations (
16) and (
17) are a 4th-order linear PDE set of
sk. Therefore, equation (
3) can be easily satisfied by multiplying the solution of Eqs. (
16) and (
17) by a constant.
Equations (16) and (17) are of the same general form:
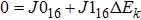 and
and
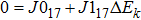 , where
, where
 and
and
 are space–time functions and
are space–time functions and
 is a space–time-independent constant satisfying
is a space–time-independent constant satisfying
 . In principle, equations (16) and (17) and
. In principle, equations (16) and (17) and
 can finally lead to a self-consistent higher-order PDE of sk, whose solution can lead to a self-consistent value of
can finally lead to a self-consistent higher-order PDE of sk, whose solution can lead to a self-consistent value of
 . In the following subsection, we explain in detail how to derive self-consistently an electron structure from Eqs. (16) and (17) and
. In the following subsection, we explain in detail how to derive self-consistently an electron structure from Eqs. (16) and (17) and
 .
.
2.2. Detailed mathematicsSolutions of Eqs. (16) and (17) are determined by the boundary conditions
 . For the simplicity of symbols, we first present a detailed formula for the isotropic case where all quantities are
. For the simplicity of symbols, we first present a detailed formula for the isotropic case where all quantities are
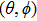 -independent. By introducing the power series expressions
-independent. By introducing the power series expressions
 and
and
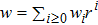 and comparing terms proportional to
and comparing terms proportional to
 in Eqs. (16) and (17) order-by-order, we can find that equations (16) and (17) lead to a recurrence formula of
in Eqs. (16) and (17) order-by-order, we can find that equations (16) and (17) lead to a recurrence formula of
 (see later Eqs. (30) and (44)). Because the isotropic parts of
(see later Eqs. (30) and (44)). Because the isotropic parts of
 and of
and of
 read as
read as
Equations (16) and (17) are of the same general form
 , where
, where
 are analytic functions of r. Note that equation (16)
are analytic functions of r. Note that equation (16)
 does not contain any terms that are proportional to
does not contain any terms that are proportional to
 and hence
and hence
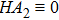 exists. In contrast, the term
exists. In contrast, the term
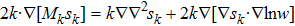 in Eq. (17) will have a contribution proportional to
in Eq. (17) will have a contribution proportional to
 ,
,
 , through
, through
 in
in
 . But another term
. But another term
 has an opposite contribution proportional to
has an opposite contribution proportional to
 , through
, through
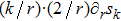 in
in
 . Therefore, equation (17) yields
. Therefore, equation (17) yields
Because of Eqs. (
20) and (
21), there exist
and
Using the power series of
 ,
,
 ,
,
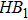 , and
, and
 , we find that equations (16) and (17) lead to
, we find that equations (16) and (17) lead to
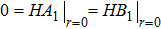 , or
, or
 . Likewise, the fact that all terms that are proportional to
. Likewise, the fact that all terms that are proportional to
 in Eqs. (16) and (17) should be 0, leads to
in Eqs. (16) and (17) should be 0, leads to
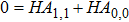 and
and
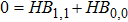 .
.
 and
and
 read as
read as
and

and
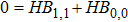
read as
Moreover, from Eq. (
17), we can express

as
where analytic functions
C0 and
C1 are defined as
Thus,
 can be written as
can be written as
or
Equation (35) requires its
 -related part to equal 0:
-related part to equal 0:
This requirement leads to
2.4. Feasibility of extension to more realistic anisotropic caseThe same procedure can be extended to more realistic anisotropic cases. UL is
 -dependent,
-dependent,
where
with

being dependent on **

. Note that **

and the spherical harmonic function

satisfy a common equation
Therefore, corresponding to the expression in Eq. (
45),
w and
sk have similar expressions

. Namely, when
UL is
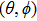
-dependent, equation (
4) will correspond to a set of equations, each of which is for all terms associated with

. The radial coefficient function

in each
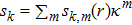
can be solved from this set, where

. Note that those
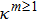
-components should warrant
Thus, for

-dependent

, we can solve, in a procedure similar to that presented previously,

and

from the

-related terms of Eqs. (
5) and (
6).