Cite this Article
Wang Cong, Guo Yong-Quan, Yang Shuo-Wang. Crystal structure and magnetic properties of disordered alloy ErGa3−xMnx. Chinese Physics B, 2019, 28(8): 086101  
Permissions
Crystal structure and magnetic properties of disordered alloy ErGa3−xMnx
Wang Cong, Guo Yong-Quan †, Yang Shuo-Wang
School of Energy Power and Mechanical Engineering, North China Electric Power University, Beijing 102206, China

 

† Corresponding author. E-mail: yqguo@ncepu.edu.cn

Abstract

ErGa3−xMnx disordered alloy is successfully prepared by the vacuum arc melting technology, and the crystal structure and magnetic properties are investigated by using the x-ray diffraction and magnetic measurements. The Rietveld structural analysis indicates that the ErGa3−xMnx crystallizes into a cubic structure with space group of 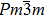in Mn doping range of x = 0–0.1. However, the disordered alloy with structural formula of (GaII, Mn)0.4 as the second phase is separated from cubic phase for the samples with x = 0.2 and 0.3, which is induced by substituting the (GaII, Mn)–(GaII, Mn) pair at 2e crystal position for the rare earth Er at 1a site. The lattice parameters tend to increase with Mn content increasing due to the size effect at Ga (1.30 Å) site by substituting Mn (1.40 Å) for Ga. The paramagnetic characteristic is observed by doping Mn into ErGa3 at room temperature. With Mn content increasing from x = 0 to 0.1, the magnetic susceptibility χ tends to increase. This phenomenon can be due to the increase of effective potential induced by doping Mn into ErGa3. However, the magnetic susceptibility χ continues to decrease with the increase of Mn content in a range of , which is due to the phase separation from the cubic Er(Ga, Mn)3 to the hexagonal Er0.8Ga2(Ga, Mn)0.4.

PACS: 61.05.cp;61.50.-f;63.50.Gh;87.80.Lg
Keyword:ErGa3-xMnx;Rietveld structure refinement;magnetic transport
1. Introduction

Most of RX3 intermetallic compounds (R = rare earth; X = In, Ga, Tl, Sn, and Pb) have a cubic AuCu3-type crystal structure.[1–8] The interest in RX3 is growing due to their salient features such as formation of magnetic moment, crystal field effect, and multiaxial magnetic structures.[9–11] In the last decade, the research activities have focused on the binary intermetallic compounds RIn3 with cubic AuCu3-type structure due to their excellent physical properties such as low temperature superconductor, complex magnetic ordering, Kondo effect, and multi-axis magnetic structure.[12–14] Gallium belongs to the IIIA group, but the RGa3 intermetallics cannot be formed between the light rare earth and Ga. In the heavy rare earth case, the stoichiometry RGa 1:3-type intermetallics only exist in a few of rare earths such as: Tm, Lu, Dy, Ho, and Er,[15,16] where TmGa3, LuGa3, and ErGa3 crystallize into a cubic AuCu3-type structure.[17] TmGa3 shows a modulated antiferromagnetic structure at low temperature, it orders antiferromagnetically around 4.2 K.[18] The saturation moment of TmGa3 is at 2 K. The two ordered phase transitions have been found in TmGa3, however their transition temperatures are very closed. The one occurs at a Néel temperature of TN = 4.26 K, and the other occurs at a quadrupole antiferromagnetic ordered temperature of TQ = 4.29 K. Below TN, the magnetism of TmGa3 shows multiaxial anisotropy with a saturation moment of at a temperature of 2 K. As for ErGa3, it shows a modulated antiferromagnetic structure at low temperature, its Néel temperature is 2.8 K, which is close to the second phase transition temperature. It indicates that these transitions occur at very low temperature, thus, it is necessary to improve the magnetic characteristics of RGa3 for developing novel room temperature diluted magnetic alloy RGa3−xTx (T = Mn, Co) by doping minor magnetic impurities such as Mn or Co and searching for its potential application as magnetoelectric functional material.

As is well known, the 3d transition metal Mn plays an important role in magnetic materials due to its significant contribution to the magnetic anisotropy by coupling with 4f electrons of the rare-earth.[19–21] Doping Mn into GdIn3 leads to a strong correlation between electric transport and magnetic state, and the electric transitions are associated with the magnetic transitions due to the Stoner spin fluctuation with the increase of temperature. In this study, Mn-diluted ErGa3 magnetic alloy is designed for providing the possibility of the exchange interaction between 3d electrons of Mn and 4f electrons of Er and for expecting to modulate the magnetic characteristics of Mn diluted in ErGa3 magnetic alloy.

2. Experimental details

The samples were prepared according to the normal structural formula of ErGa3−xMnx (x = 0–0.3) and the purities of raw metals were higher than 99.9 wt%. Owing to the evaporation loss of Er and Mn in the melting process, their weights are appropriately compensated for by supplying extra contents for Er: 1%∼2% and Mn: 8%∼10%. The samples were melted in the non-consumable vacuum arc furnace under atmosphere of high pure argon gas. Each sample was re-melted four times to ensure the homogeneity, and followed by being annealed at 800 °C for 168 h in the evacuated quartz tube in order to eliminate the residual stress, and finally by quenching in water.

2.1. Crystal structure analysis

The crystal structures of samples were determined by x-ray diffraction (XRD) with Cu–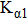 radiation, and then the diffraction data were selected for determining crystal structure with TREOR and Rietveld powder diffraction profile fitting technique.

2.2. Magnetic property analysis

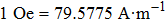
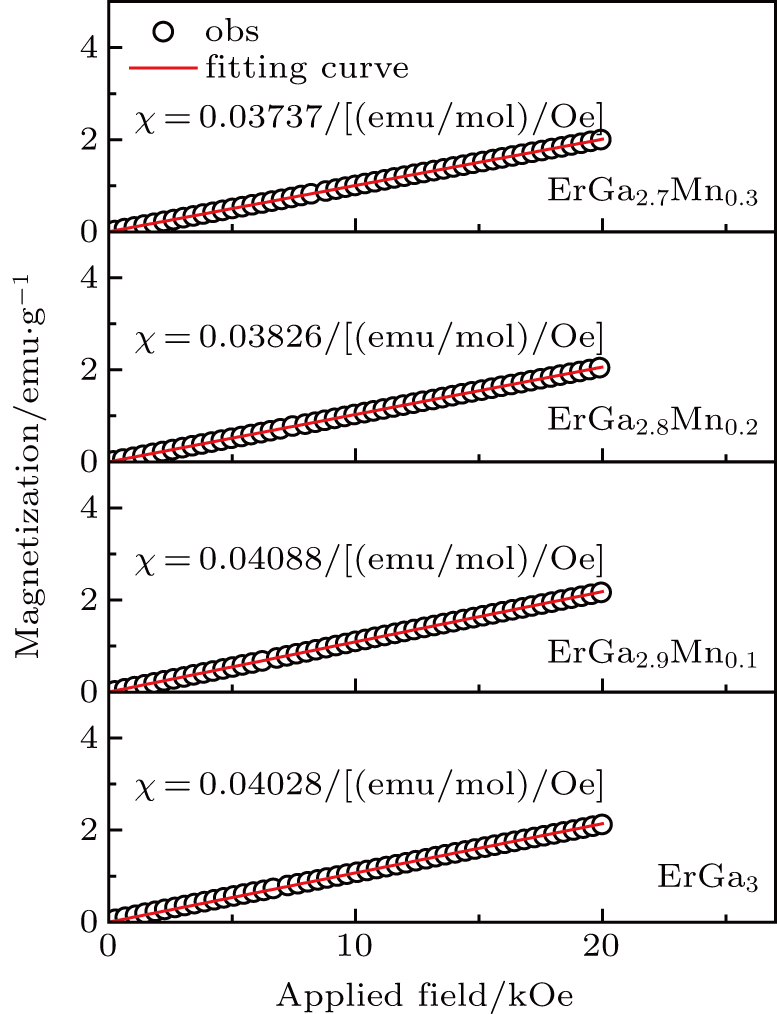
The field dependence of magnetization curves (M–H) were measured with a vibrating sample magnetometer (VSM) under the applied fields ranging from −20 kOe ( ) to 20 kOe at room temperature.

3. Results and discussion
3.1. Crystal structure

As shown in Fig. 1(a), the XRD patterns show that ErGa3−xMnx alloys are of single phase for x = 0 and 0.1, the satellite peaks of the second phase are present in the other two samples with x = 0.2 and 0.3. These peaks can be indexed by a hexagonal structure with a group of P6/mmm. The planar indices show that the lattice parameters and the crystal cell volumes of cubic phase increase monotonically with the increase of Mn content as listed in Table 1. It is due to the size effect at Ga site. The atomic radii are 1.73 Å for rare earth Er, 1.30 Å for Ga, and 1.40 Å for Mn, respectively. Since the atomic radius of Mn is larger than that of Ga, the substitution of Mn for Ga causes both the lattice parameters and the unit cell volumes to increase. Figure 1(b) is the enlarged plot of Fig. 1(a) around the strongest diffraction peak (111) of cubic phase, and it is very clear that the (111) peak shifts toward the low angle with the increase of Mn content, which causes the planar distance to increase and induces the lattice parameters to augment.

Fig. 1. XRD patterns of (a) ErGa3−xMnx alloys and (b) enlarged patterns in 2θ ranging from 32° to 38°.
Table 1.

Lattice parameters of cubic ErGa3−xMnx alloys.

.
3.2. Rietveld structure refinement

The crystal structure of ErGa3−xMnx was refined by using the Rietveld refinement method. Figures 2(a)–2(d) show the refined XRD patterns of ErGa3−xMnx alloys, where the measured and calculated XRD patterns are marked with the symbol of “+” and solid lines, respectively. The lowest trace indicates the differences between the two patterns. Based on the structural refinement, ErGa3−xMnx crystallizes into a cubic AuCu3-type structure with a space group of in an Mn content range of .The atomic occupations correspond to 1a (0, 0, 0) site for Er atoms, and 3c (0, 1/2, 1/2) site for (Ga, Mn) atoms. The lattice parameter a = 4.2155 Å–4.2416 Å. The crystallographic data are supplied in Tables 2 and 3. In the regime of , the disordered hexagonal phase coexists with the cubic phase and its structural formula is (GaII, Mn)0.4, and it can be considered as the derivation of cubic ErGa 1:3 phase; if the number of Er atoms is normalized, the structural formula is written as ErGa2.5(Ga, Mn)0.5, i.e., Er(Ga, (GaII, Mn)0.4Mn) 1:3. Thus, the disordered Er(Ga, Mn)3 alloy is of hexagonal phase. There are three kinds of nonequivalent crystal positions in this disordered hexagonal unit cell, which are occupied by Er at 1a site, GaI at 2d site, and (GaII, Mn) at 2e, respectively. The phase formation is induced by substituting the (GaII, Mn)–(GaII, Mn) pair at 2e crystal position for rare earth Er at 1a site. According to the refined results, the corrected formulae of ErGa3−xMnx cubic phase are ErGa2.91Mn0.09 for x = 0.1, ErGa2.79Mn0.21 for x = 0.2, and ErGa2.71Mn0.29 for x = 0.3, respectively. The formulae of disorderedly hexagonal phase are Er0.8Ga2(Ga0.88Mn0.12)0.4 for x = 0.2 and Er0.8Ga2(Ga0.10Mn0.90)0.4 for x = 0.3. Since the Mn content increases in the two phases, their lattice parameters and unit cell volumes rise up correspondingly. The content of muti-phase can be determined from the following formula according to the structural refinement parameters:[22]

where ωi is the weight percentage of the i-th phase, Si, Zi, Mi, and Vi represent the scale factor, the number of formula units per unit cell, molecular weight, and cell volume in the i-th phase. The calculated weight percentages of ErGa2.79Mn0.21, Er0.8Ga2(Ga0.88Mn0.12)0.4, ErGa2.71Mn0.29, and Er0.8Ga2(Ga0.10Mn0.90)0.4 are 92.58%, 7.42%, 91.55%, and 8.45%, respectively.

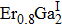
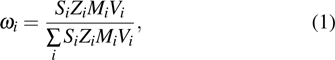Fig. 2. Observed and calculated XRD patterns of ErGa3−xMnx for (a) x = 0, (b) x = 0.1, (c) x = 0.2, and (d) x = 0.3.
Table 2.

Rietveld refinement structural parameters of ErGa3−xMnx.

.
Table 3.

Rietveld refinement structural parameters of (GaII, Mn)0.4.

.

The bond lengths in ErGa3−xMnx intermetallic compounds are calculated according to the refined atomic coordinates and the results are shown in Figs. 3(a)–3(c). Since the radius of Mn atom (1.40 Å) is larger than that of Ga atom (1.30 Å), doping Mn into ErGa3 causes both the lattice parameters and the unit cell volume to increase, which induces significantly the lattice to distort through prolonging the Er–Er, Ga–Ga, and Er–Ga bond lengths as listed in Table 4. The driving force for forming the disordered Er0.8Ga2(Ga, Mn)0.4 phase might be due to the lattice distortion. The substitution of Mn for Ga reduces the effective atomic radius ratio between Er and (Ga, Mn) and forms the structural skeleton of Er0.8Ga2(Ga, Mn)0.4. The projections of unit cells for the two structures reveal that the phase transformation from the cubic ErGa3 to hexagonal Er0.8Ga2(Ga, Mn)0.4 originates from the rotation of M6 (M = Ga, Mn) hexagonal ring.[23] Comparing with the projection along the [111] direction in ErGa3, the M6 hexagonal ring rotates an angle of 30° in Er0.8Ga2(Ga, Mn)0.4 as shown in Fig. 4.

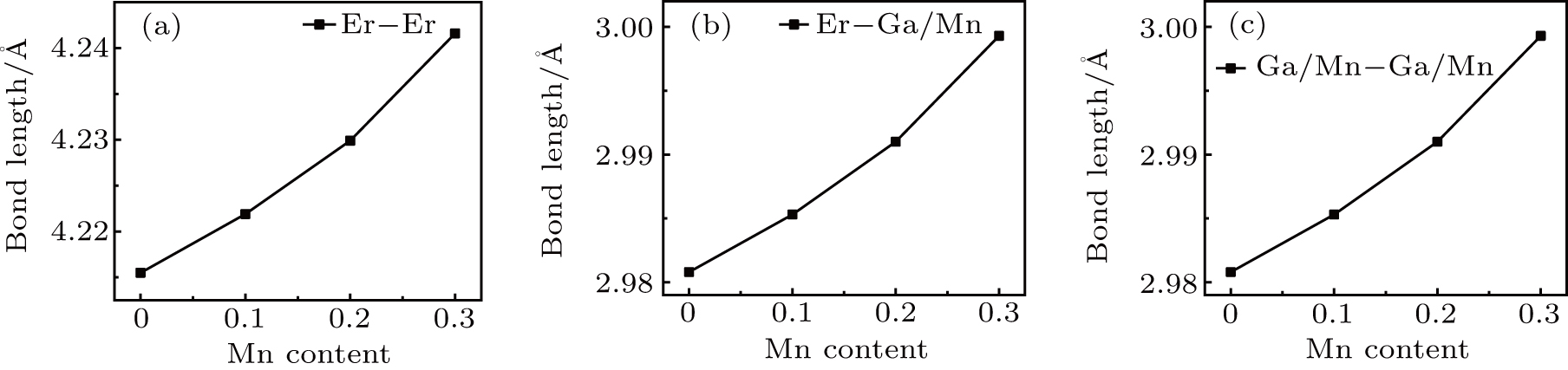Fig. 3. Mn content-dependent bond lengths of ErGa3−xMnx compounds for (a) Er–Er, (b) Er–(Ga, Mn), and (c) (Ga, Mn)–(Ga, Mn).
Fig. 4. Projections of cubic ErGa3 along [111] direction and hexagonal ErGa2(Ga, Mn)0.4 along [001] direction for (a) cubic structure and (b) hexagonal structure.
Table 4.

Bond lengths of cubic ErGa3−xMnx.

.
3.3. Magnetic properties

Figure 5 shows the observed and fitted magnetization curves by using vibrating sample magnetometer (VSM) at room temperature, where the symbols of circle and solid lines are corresponding to the observed and fitted magnetization, respectively. The ErGa3−xMnx is paramagnetic based on its linear magnetizing characterization through fitting the following equation:

where M, χ, and H are corresponding to the magnetization, paramagnetic susceptibility, and external field. The magnetization rises up with Mn content increasing and reaches the saturation level at Mn content of x = 0.1. The fitting parameters are listed in Table 5. The Mn content-dependent a and V, susceptibility χ are shown in Figs. 6(a) and 6(b), respectively. The paramagnetic susceptibility variation tendency can be due to Mn ion and Er ion increasingly contributing to effective moments, however, the susceptibility comes down in the two-phase regime of , which can be due to the presence of second phase Er0.8Ga2(Ga, Mn)0.4, and the phase content of the second phase increasing with Mn content. According to Mn content dependence of susceptibility shown in Fig. 6(b) and Mn–Mn bond lengths listed in Table 4, the lattice distortion relative to the paramagnetic susceptibility, the prolongations of Er–Er and Mn–Mn bond lengths cause the susceptibility to decrease in the two-phase region.

Fig. 5. Observed and fitted magnetization curves of ErGa3−xMnx alloys at room temperature.
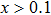
Fig. 6. Curves of Mn content-dependent fitted parameters of ErGa3−xMnx for (a) lattice parameter a and volume V, and (b) susceptibility χ.
Table 5.

Fitted parameters of ErGa3−xMnx.

.
4. Conclusions

The Mn doped ErGa3−xMnx alloys crystallize into cubic structure with a space group of in a range of x = 0–0.1. The phase separation from cubic phase to disordered hexagonal phase occurs in each of the samples with x = 0.2 and 0.3. Rietveld structural refinements show that the structural formula of disordered hexagonal phase is (GaII, Mn)0.4 with the space group of P6/mmm and Z = 2. There are three kinds of nonequivalent crystal positions in unit cell, which are occupied by Er at 1a site, GaI at 2d site, and (GaII, Mn) at 2e, respectively. The phase formation of disordered hexagonal phase is induced by substituting the (GaII, Mn)–(GaII, Mn) pair at 2e crystal position for the rare earth Er at 1a site. The lattice parameters tend to increase with Mn content increasing due to the size effect at Ga (1.30 Å) site by substituting Mn (1.40 Å) for Ga.

The ErGa3−xMnx alloys show paramagnetic characteristics at room temperature. With the increase of Mn content in a range of x = 0–0.1, the magnetic susceptibility χ increases due to the Mn ion and Er ion increasingly contributing to effective moment. However, the magnetic susceptibility χ decreases with Mn content increasing, which is due to the phase separation from the cubic Er(Ga, Mn)3 to Er0.8Ga2(Ga, Mn)0.4. The lattice distortion is the phase transition driving force and causes the Er–Er and Mn–Mn bond lengths to be prolonged, which induces the susceptibility to decrease.

Reference
1 Buschow K H J 1979 Rep. Prog. Phys. 42 1373 https://doi.org/10.1088/0034-4885/42/8/003
2 Lawrence J 1979 Phys. Rev. B 20 3770 https://doi.org/10.1103/PhysRevB.20.3770
3 Bross H 2011 Adv. Cond. Matter Phys. 2011 867074 https://doi.org/10.1155/2011/867074
4 Belyavina N Nakonechna O Babich M Markiv V 2015 J. Alloys Compd. 643 137 https://doi.org/10.1016/j.jallcom.2015.04.148
5 Solyga A Czopnik A Pluznikov V Ulner J Durczewski K Kletowski Z 2006 European Conference on Physics of Magnetism (PM 05) June 24–27, 2005 Poznan, Poland p. 159 https://doi.org/10.1002/pssc.200562484
6 Pluzhnikov V B Grechnev G E Czopnik A Eriksson O 2005 Low Temp. Phys. 31 313 https://doi.org/10.1063/1.1884445
7 Slater B R Bie H Y Stoyko S S Bauer E D Thompson J D Mar A 2012 J. Solid. State. Chem. 196 409 https://doi.org/10.1016/j.jssc.2012.07.009
8 Pluzhnikov V B Czopnik A Svechkarev I V 1995 Physica B 212 375 https://doi.org/10.1016/0921-4526(95)00382-j
9 Kletowski Z 1992 Solid. State Commun. 83 241 https://doi.org/10.1016/0038-1098(92)90845-Z
10 Shafiq M Ahmad I Asadabadi S J 2014 J. Appl. Phys. 116 103905 https://doi.org/10.1063/1.4894833
11 Chen S L Guo Y Q He Q 2015 J. Appl. Phys. 117 123910 https://doi.org/10.1063/1.4916338
12 Kletowski Z Fabrowski R Slawiński P Henkie Z 1997 J. Magn. Magn. Mater. 166 361 https://doi.org/10.1016/S0304-8853(96)00671-3
13 Kletowski Z 2000 Supermaterials Netherlands Springer pp. 163–172 https://doi.org/10.1007/978-94-010-0912-6_16
14 Kletowski Z Czonpnik A Tal A Boer F D 2000 Physica B 281–282 163 https://doi.org/10.1016/S0921-4526(99)01184-9
15 Cirafici S Franceschi E 1981 J. Less. Comm. Met. 77 269 https://doi.org/10.1016/0022-5088(81)90179-X
16 Murtaza G Gupta S Seddik T Khenata R Alahmed Z Ahmed R Khachai H Jha P Omran S 2014 J. Alloys Compd. 597 36 https://doi.org/10.1016/j.jallcom.2014.01.203
17 Morin P Giraud M Regnault P L Roudaut E Czopnik A 1987 J. Magn. Magn. Mater. 66 345 https://doi.org/10.1016/0304-8853(87)90168-5
18 Fulfer B W McAlpin J D Engelkemier J McCandless G T Prestigiacomo J Stadler S Fredrickson D C Chan J Y 2014 Chem. Mater. 26 1170 https://doi.org/10.1021/cm4035424
19 Negri D Kaczorowsiki Grytsiv Alleno Giovannini 2004 J. Alloys Compd. 365 58 https://doi.org/10.1016/S0925-8388(03)00657-1
20 Singh S Dhar S Manfrinetti P Palenzona A 2002 J. Magn. Magn. Mater. 250 190 https://doi.org/10.1016/S0304-8853(02)00380-3
21 Dhar S Manfrinetti P Palenzona A 2002 Solid. State. Commun. 124 379 https://doi.org/10.1016/S0038-1098(02)00624-5
22 Hill R J Howard C J 1987 J. Appl. Crystallogr. 20 467 https://doi.org/10.1107/S0021889887086199
23 He Q Guo Y Q 2016 Appl. Phys. A 122 1 https://doi.org/10.1007/s00339-015-9525-1