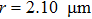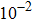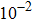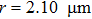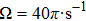† Corresponding author. E-mail:
Manipulating biomacromolecules and micro-devices with light is highly appealing. Opto driving torque can propel micro-rotors to translational motion in viscous liquid, and then separate microsystems according to their handedness. We study the torque of dielectric loss generated by circular polarized lasers. The unwanted axial force which causes the handedness independent translational motion is cancelled by the counter propagating reflection beams. The propelling efficiency and the friction torque of water are obtained by solving the Navier-Stokes equation. In the interesting range of parameters, the numerical friction torque is found to be linear to the angular velocity with a slope depending on the radius of rotor as r 3. The time-dependent distribution of angular velocity is obtained as a solution of the Fokker–Planck equation, with which the thermal fluctuation is accounted. The results shed light on the micro-torque measurement and suggest a controllable micro-carrier.
People have been interested in the separation of micro-systems with different handedness by propeller effect for many years.[1–6] Various optical techniques have been implemented for rotating or propelling biomacromolecules[7] or microelectromechanical systems[8–14] and for direct measurement of micro-torque. It has been known that the rotating electric field can induce a constant torque to a polarizable conductive particle,[15–18] whose dipole rotates at the same frequency as the electric field but not synchronously due to the conductance or dielectric loss.[19] Early demonstrations depend on the breaking rotational symmetry of the particle or the trapping beam.[20–24] Friese et al. have shown that both linearly and circularly polarized lights can rotate a microscopic birefringent particle.[21] It has been shown that the angular optical trap exerts torque on individual biological molecules.[25,26] A designed nano-turbine driven by fluid flow has been simulated with molecular dynamics.[27] The researchers found that the rotational angular velocity has a robust linear relationship with the fluid flow velocity. And the ratio of the angular velocity to the translational velocity is much smaller than the ideal value, implying a large edge effect on propelling efficiency for the nano-turbine. A natural question is: how small is a system whence its edge effect becomes important? For applications, people also concern over the feasibility and the efficiency of optical separation of microsystems or biomacromolecules with different handedness and over how they depend on the structure of the system and the temperature. To answer these questions, quantitative calculations which depend on the system parameters are required.
We carry out a qualitative calculation/simulation for the propeller effect of a special type of micro-systems with different handedness driven by rotating electric fields. Our target is very similar to a recent work by Makino and Doi.[18] But unlike their particle that has a permanent electric dipole, we consider the microsystems with different handedness that are made in a dielectric material without permanent electric dipole. We investigate both rotational and translational motions of a micro-rotor immersed in water, simulate a micro-biological system or micro-machine in living/working environment. The micro-rotor is driven by circularly polarized laser beams. We are interested in the opto torque originated from the dielectric loss that leads to handedness-depending translational motion through the propeller effect. In contrast, the translational motion caused by direct momentum transfer in photon scattering do not depend on the handedness of the rotor. To cancel the force and torque from direct momentum transfer, we propose to use two laser beams, both of them propagate along the axis but in opposite directions.
The hydrodynamics of the micro-rotor in water is described by the Navier–Stokes equation. In principle, it gives the propelling efficiency and the friction torque, which are two crucial quantities in the present paper. However, a general solution for our model is still laking because of the significant edge effect of the micro-rotor. Therefore we will partially resort to numerical simulation. Numerical friction torque exhibits a cubic scaling law in the regime of small Reynolds number, that is consistent with the dimension analysis. The cubic scaling law is broken at a radius of hundred micrometers, revealing the crossover from the micro-sized regime to the macro-sized regime where the edge effect is less important and the fluid on the blade surface can be described by the model of laminar boundary layer.
Moreover, the thermal fluctuation that competes with the hydrodynamic motion is also significant for small Reynolds number. It will be accounted by random torques. Langevin-like stochastic equation of motion is converted into the Fokker–Planck equation. The later is solved to obtain the time-depending distribution of angular velocity. Combining the propelling efficiency from the simulation, we obtain the time-dependent translational velocity for a representative micro-rotor made with graphite and carbon microtube.
In the following, the model and the theoretical framework are described in Section 2. In Section 3 the opto driving torque is derived and the scaling behavior of the friction torque is discussed based on a general dimension analysis as well. Section 4 gives the solution of the Fokker–Planck equation for time-depending distribution of the angular velocity in the regime of small Reynolds number. Section 5 describes the numerical solution of the Navier–Stokers equation. The translational velocity is obtained for specific parameters of the material and laser in Section 6. Summary is given in the last section.
We consider a micro-rotor that consists of a carbon microtube (CMT)[28] and three symmetric graphite blades, as shown in Fig.
The micro-rotor is driven by two counter propagating circularly polarized laser beams as shown in Fig.
In Fig. 
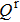
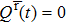

The driving torque rotates the micro-rotor and concomitantly the thrust force of liquid sets up the translational motion. The velocity field of the incompressible viscous liquid satisfies the Navier–Stokes equation
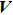

It is well known that the Navier–Stokes equation is simplified to the linear Stokes equation by dropping the nonlinear term of Eq. (
The average driving torque on unit volume of blades during a period of light, produced by the circularly polarized laser, is given by[29]
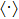

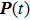





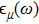
We concentrate on the torque along z axis, exerting on area 
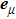
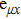

The circularly polarized laser has electric field 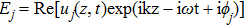


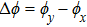
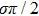
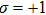
The dielectric loss is characterized by the imaginary part of permittivity 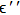
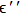

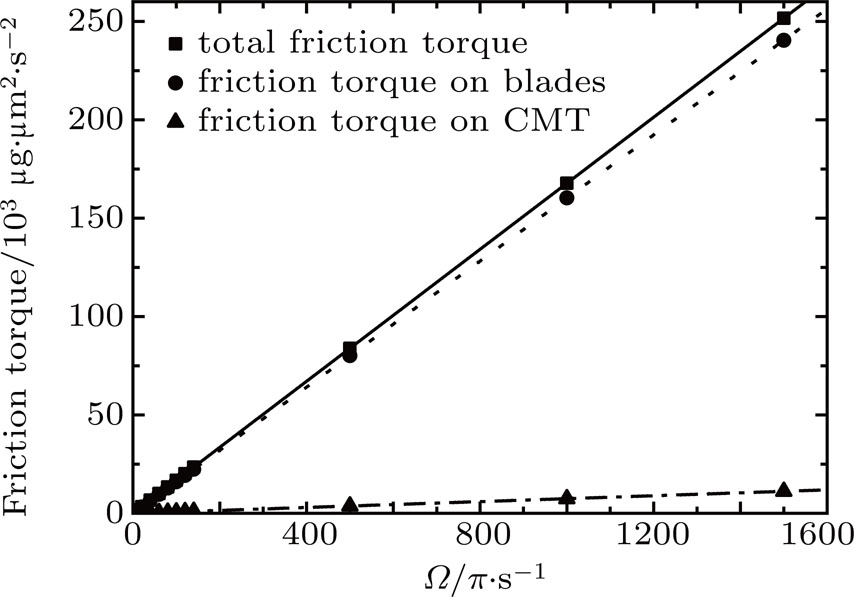
The friction torque on the rotor is given by

It is very difficult if not impossible to obtain Q f analytically because the complicated boundary. Before getting to the results of numerical simulation in Section 5, let us discuss the scaling behaviors in the small and large Reynolds number regimes.
The friction torque acts as a resistance to the rotational motion of the rotor. One can express the friction torque as



For small Reynolds numbers, the constant term of Eq. (
For large r but slow rotation, the edge effect is less important and the flow near to the surface of blades can be considered as a 2D laminar boundary layer flow. In this case the second term of Eq. (
The coefficients c
n (n=0,1,2) depend on the structure, for example the tilt angle β, and the boundary conditions. Generally they can only be obtained by numerical calculation. But for a thin disk plate with large radius thus the edge effect is negligible there is an analytical solution 
In this section we concentrate on the linear regime of the Navier–Stokes equation. Adopting Eq. (
Solving Eq. (
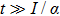


The stochastic process can be described by the time-depending probability distribution of the angular velocity which satisfies the Fokker–Planck equation. The Fokker–Planck equation related to Eq. (
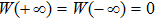
The general non-stationary solution is obtained by the Fourier transformation and the method of characteristics. Defining 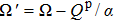

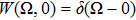

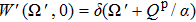

At each moment t, Ω has a Gaussian distribution with the mean


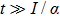

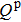

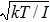
The rotor is propelled forward in the liquid by the laser beams. The rotating machinery with laminar flow interrface is used in the study. No boundary slip at the interface between fluid and rotating rotors is applied, i.e., the fluid has no relative velocity to the solid at the fluid–solid interface. We adopt the inertial frame of reference in which the rotor has no translational motion, while the flow at infinity has a constant axial velocity. In simulation, the rotor is placed at the center of a water-filled cylinder vessel with the radius of 
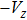
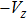
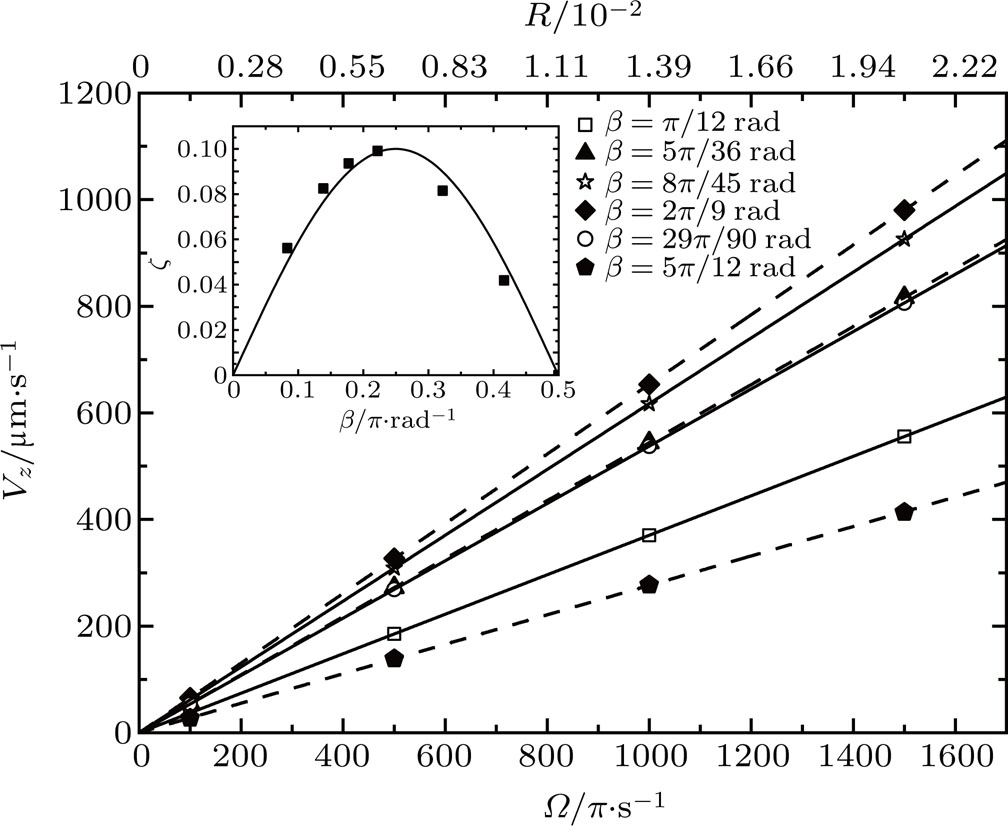
We first simulate a representative micro-rotor whose axle has radius of 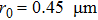
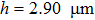


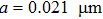

Then rotors with various tilt angles β and radii r=0.21, 2.10, 


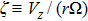


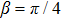

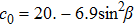
To explore the scaling crossover from small to large Reynolds numbers, rotors of β=32° and thin disks with r ranged from 


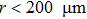
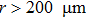

To be specific, the wave length of the driving laser is chosen to be 543 nm and the amplitude of electric field 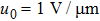
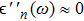
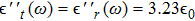
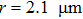
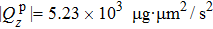
We again concentrate on the small Reynolds regime where the friction torque is linear with the angular velocity. Adopting the numerical c
0 and the corresponding α for the representative micro-rotor obtained in the simulation, we plot the probability density 
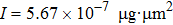
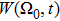



 | Fig. 7. The time-dependent probability density 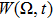
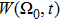
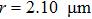
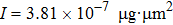
|
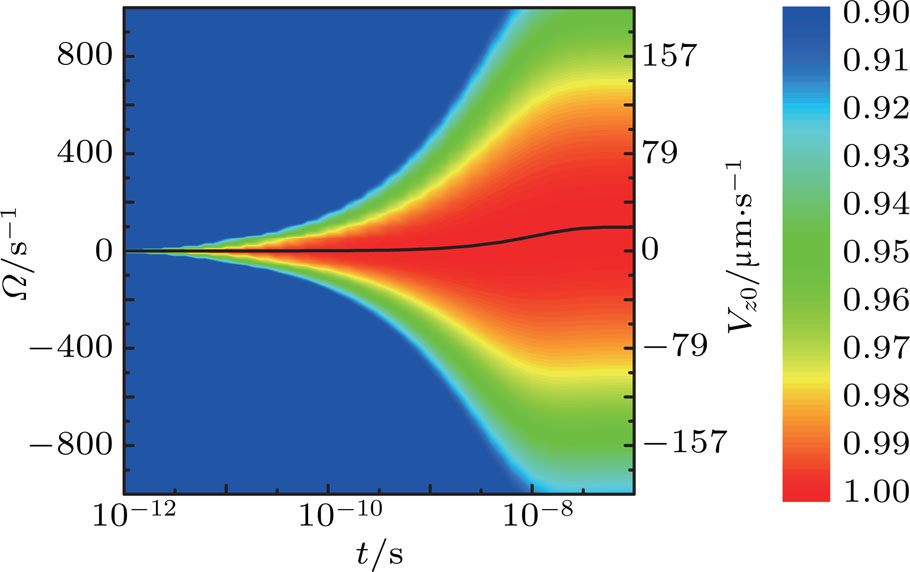 | Fig. 8. The time-depending normalized probability density 

|
From Fig. 



In summary, we investigate the hydrodynamic behavior of the micro-rotor model, which is rotated by two counter-propagating circularly polarized laser beams. The direct momentum transfer in photon scattering is canceled, while the dielectric loss contributes to a finite and controllable driving torque that propels the micro-rotor to translational motion in the direction depending on the handedness. The friction torque and the propelling efficiency as two essential quantities of the problem are calculated. In the range of radius 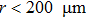
In the small Reynolds number regime, the stochastic fluctuation of the angular velocity as a function of time is obtained as the solution of the Fokker–Planck equation. The fluctuation is about an order higher than the mean value for the representative micro-rotor. It can be reduced by increasing the moment of inertia. The steady mean angular velocity is 

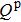
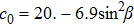

Driving by circularly polarized laser with a feasible field strength of 1 V/
We thank Flytzanis for drawing our attention to this topic and having valuable discussions. The authors also thank the reviewers for suggesting the method of dimension analysis and for providing valuable references.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] |