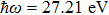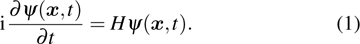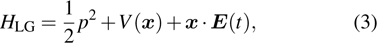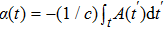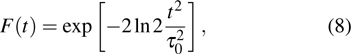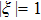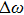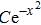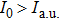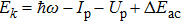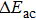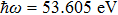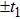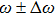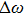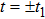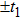Interference effect of photoionization of hydrogen atoms by ultra-short and ultra-fast high-frequency chirped pulses
1. IntroductionAfter the invention of chirped pulse amplification (CPA) technique,[1] the power of laser increases very rapidly. People can produce now stronger and stronger,[2,3] as well as shorter and shorter[4–6] ultrafast laser pulses. Recent years, the free electron laser (FEL) light sources such as extreme light infrastructure (ELI), are designed to generate super-intense laser intensities of the order of 1023 W/cm2–1024 W/cm2.[7] With such intense laser intensity and high frequency as the new tool to explore the physics, there are some new physics and fantastic phenomena expected to be found. For example, when laser intensity is above 3.51×1016 W/cm2, the ionization of hydrogen atoms does not increase with the build-up of laser envelop, the ionization process will be suppressed until the laser electric field decrease to some level, this is so called atomic stabilization effect.[8]
When matter encounter high laser intensity that well beyond the single atomic unit intensity (3.51×1016 W/cm2), not only the ionization rate will be modified, but also many more other interesting effects are accompanied. For instance, the ac Stark shift will significantly change the energy levels of atomic systems, including the energy level of ground state.[9,10] When the dynamic changing energy levels encounter ionization and atomic stabilization, the dynamic interference effect occurs.[11–13] Recently there are some discussions on the interference fringes in the first above threshold ionization peak of the photoionization of ground state hydrogen atoms[12–20] and helium atoms.[21] Although there are some studies shown no dynamic interference effect can be observed for photon energy within 100 eV,[15–17] Guo et al. observed the dynamic interference with photon frequency
 . And they found that dynamic interference emerge for very short pulses (5 or 10 optical cycles, o.c.) and disappear at longer pulses (40 o.c.).[12] It is reasonable through the previous investigation on atomic stabilization for laser frequencies no less than 1 atomic units (a.u.).[22] Conclusion from Guo et al. also agrees well with Jiang et al.’s findings for photon energy
. And they found that dynamic interference emerge for very short pulses (5 or 10 optical cycles, o.c.) and disappear at longer pulses (40 o.c.).[12] It is reasonable through the previous investigation on atomic stabilization for laser frequencies no less than 1 atomic units (a.u.).[22] Conclusion from Guo et al. also agrees well with Jiang et al.’s findings for photon energy
 with pulse durations between 0.2 fs–2 fs.[13] To observe the dynamic interference in the ionization from the ground state of hydrogen atoms at a moderately high laser frequency (e.g., 53.605 eV), it requires the peak intensity about 1018 W/cm2 or higher.[13] Such an intensity might result in breaking down of dipole approximation, Wang et al. investigated how the nondipole effect changes atomic dynamic interference. They found that the dynamic interference is suppressed even with nondipole approximation, it will be persisted in the photoelectron momentum distributions.[18]
with pulse durations between 0.2 fs–2 fs.[13] To observe the dynamic interference in the ionization from the ground state of hydrogen atoms at a moderately high laser frequency (e.g., 53.605 eV), it requires the peak intensity about 1018 W/cm2 or higher.[13] Such an intensity might result in breaking down of dipole approximation, Wang et al. investigated how the nondipole effect changes atomic dynamic interference. They found that the dynamic interference is suppressed even with nondipole approximation, it will be persisted in the photoelectron momentum distributions.[18]
All investigations above are performed with a finite duration pulse. Such a pulse has a finite spectral width, which means it is not purely monochrome laser, it contains electromagnetic field with different frequencies in a range. When light transmit through a lens such as in experiment, chirp will be introduced to the laser pulse due to the different frequencies of pulse. It has been known that chirped attosecond pulse is an effective method to control electronic dynamics.[23–25] Recently, there has been widespread interest in the studies of interaction between atoms/molecules and strong chirped laser pulses.[26–31]
It is interested to see the effect of a chirp attosecond pulse on the dynamic interference of the ground state hydrogen atoms. Does adding chirp will enhance or weaken the dynamic interference? In this work, we will investigate the effect of chirped pulses on dynamic interference by numerically solving the time-dependent Schrödinger equation (TDSE).
The rest of this paper is organized as follows: in the Section 2 we introduce the theoretical method of studying the ionization process of ground state hydrogen atoms; then in Section 3 we discuss the how a chirped pulse with high carrier frequency change the dynamic interference of photoelectron spectrum, and its dependence on the chirp parameters, pulse durations and laser intensities; the conclusions are finally made in the Section 4.
Unless specifically stated otherwise, the atomic units (a.u.) are used throughout this paper.
2. Theory and modelsAn ab initio numerical framework is briefly presented in this section. To investigate the photoionization of ground state hydrogen atoms, we numerically solve the TDSE for single electron atoms, which reads
The form of the Hamiltonian
H is dependent on the choice of gauge. The choice of electromagnetic gauge of laser field has a large influence on the numerical simulation effort involved in strong field calculations. As indicated above, the hydrogen atoms are subjected to super-intense laser pulses with peak intensity about or above
Ia.u. = 3.51×10
16 W/cm
2, which are beyond the perturbative regime. In this case, we have to very carefully take care of our numerical simulation. For example, as previously pointed out by Baghery
et al.[17] and Jiang
et al.,
[18] the choice of gauge and insufficient of angular momentum
l might result in unconverged results.
[17,19]To avoid all these possible problems, we start our investigation by ab initio calculation with three different gauges: (i) velocity gauge (VG);[32] (ii) length gauge (LG);[32] and (iii) Kramers–Henneberger (KH) frame, which is frequently adopted to investigate the atomic stabilization effect.[33] Here we give the Hamiltonian H of these three gauges, respectively:
where

is a soft-core model potential of one-dimensional hydrogen atoms, and we set the soft core parameter
a = 2 to obtain correct ground state energy
Eg = 0.5.
[34] The parameter

in KH frame stands for the motion trajectory of a free electron in the intense laser pulse,
[35] it has the form
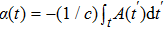
.
[8,35] Due to the softcore potential cannot exactly represent a real hydrogen atomic potential, the atomic stabilization effect and dynamic interference are easier to accomplish.
[8,13] To obtain the same level dynamic interference with the same pulse duration, one-dimensional softcore potential requires weaker laser intensity than that of three-dimensional real Coulomb potential. However, all physical mechanism and features are the same.
[13]We use a Gaussian envelope for the vector potential A(t) of a linearly polarized laser pulse along the x axis which can be written as
where
ξ is the chirp parameter. Its chirped peak amplitude
A(
ξ), chirped carrier frequency
ω, and time-dependent envelop
F(
t) are expressed respectively by
[30]
where
Ia.u. = 3.51×10
16 W/cm
2 is the atomic unit of laser intensity. The case
ξ = 0 means the Fourier transform-limited pulse with peak intensity
I0, carrier frequency
ω0, and pulse duration
τ0 (full width at half maximum, FWHM). And the the electric field
E(
t) can be obtained from the the vector potential
A(
t) of the pulse by
 | |
In Fig. 1 we schematically display laser field information of radiative pulses in the form above. The black-solid curves stand for chirp-free case, and red-dashed curves depict the ξ = −1 pulses, and the blue-dashed-dotted curves indicate the positive ξ = 1 results. The graph (a) depicts the vector potential versus time of the laser pulses. In the pulse center (t = 0), the chirped and chirp-free pulses are overlapped. The negative (positive) chirped pulse has the highest (lowest) frequency at
 and lowest (highest) frequency at
and lowest (highest) frequency at
 of the three pulses here, as shown by the time-dependent instantaneous frequency with different chirp parameters in Fig. 1(c). Figure 1(b) presents spectral profiles. Both negative and positive chirped pulses with same absolute
of the three pulses here, as shown by the time-dependent instantaneous frequency with different chirp parameters in Fig. 1(c). Figure 1(b) presents spectral profiles. Both negative and positive chirped pulses with same absolute
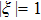 have same power spectrum. They are wider than the chirp-free result which is the Fourier-transform limit. To keep the same pulse envelop as chirped-free pulse, the chirped pulses have wider spectrum. We also notice that the instantaneous frequency deviates largely from central frequency ω0 = 53.6 eV. From Eq. (7), at time t = τ0,
have same power spectrum. They are wider than the chirp-free result which is the Fourier-transform limit. To keep the same pulse envelop as chirped-free pulse, the chirped pulses have wider spectrum. We also notice that the instantaneous frequency deviates largely from central frequency ω0 = 53.6 eV. From Eq. (7), at time t = τ0,
 , a shorter pulse gives larger deviation of the instantaneous frequency. For later discussion in this work, we choose τ0 = 6 fs and 30 fs,
, a shorter pulse gives larger deviation of the instantaneous frequency. For later discussion in this work, we choose τ0 = 6 fs and 30 fs,
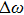 takes the values 0.129 eV and 0.026 eV at
takes the values 0.129 eV and 0.026 eV at
 , respectively. They are much smaller than what is shown in Fig. 1(c) here.
, respectively. They are much smaller than what is shown in Fig. 1(c) here.
Then, after substituting the Hamiltonian into Eq. (1), it can be solved by splitting the Hamiltonian H into V/2+T+V/2 as follows:
The initial state
ψ(
t = 0) is obtained by replacing the real time
t in TDSE with the imaginary time

, and starting with an arbitrary wave packet, here we use a Gaussian wave packet
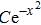
, where
C is a normalization factor.
3. Results and discussionsAll calculations in this section are carried out using numerical grids with box sides between 2×103 and 2×104, and grid points on between 2×104 and ×105 respectively. The time steps in each optical cycle is 1024. With all these settings we are able to obtain 4–5 digits in the momentum resolution. Based on our ab initio numerical simulations of the TDSE, we investigated the dynamic interference effect in the photoionization of ground state hydrogen atoms in the presence of super-intense (e.g., with peak intensity
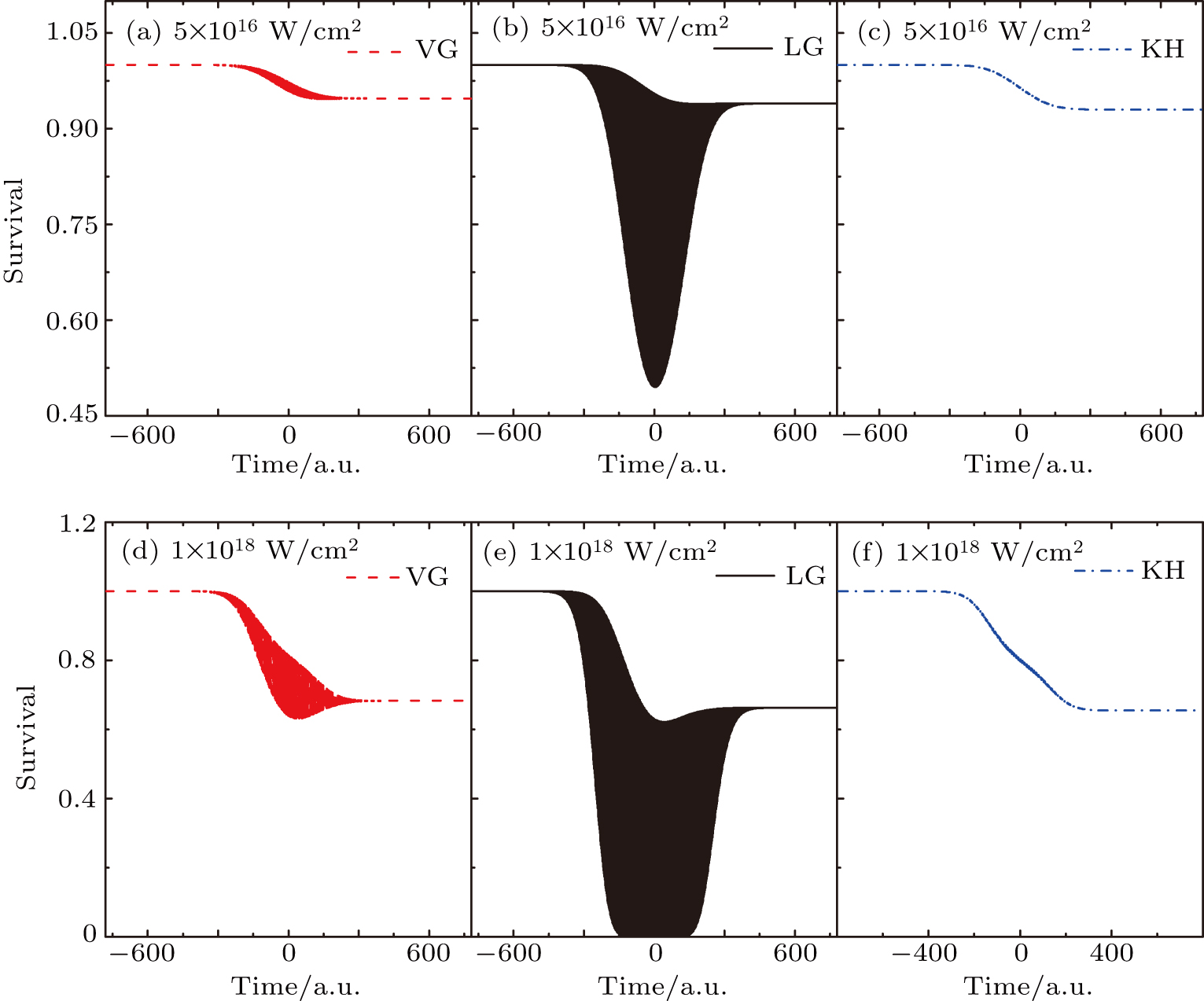
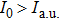 ) chirped laser pulses. Follow previous investigations by Demekhin et al.,[20] Baghery et al.,[17] Jiang et al.,[13] and Wang et al.,[18] we also use the same central frequency of laser pulse with ω = 53.605 eV. First, in Fig. 2 we display the survival of ground state in the presence of laser field with different intensities. The laser intensity and gauge for each graph are indicated in the figure. With relative weak field (5×1016 W/cm2), the depletion is small, most atoms stay at ground state. Around the peak of pulse, the LG curve shows most dramatic oscillation in survival. The KH frame gives the smoothest curve. However, all three gauges are converged to the same survival and depletion. When much stronger laser field (1×1018 W/cm2) is applied, in the three graphs of right panels, we observe completely depletion of ground state in the LG curve around the peak of pulse. The VG curve also shows strong oscillation in the survival. While the KH frame result again has the smoothest survival curve. And all results from three gauges are the same at the end of pulses.
) chirped laser pulses. Follow previous investigations by Demekhin et al.,[20] Baghery et al.,[17] Jiang et al.,[13] and Wang et al.,[18] we also use the same central frequency of laser pulse with ω = 53.605 eV. First, in Fig. 2 we display the survival of ground state in the presence of laser field with different intensities. The laser intensity and gauge for each graph are indicated in the figure. With relative weak field (5×1016 W/cm2), the depletion is small, most atoms stay at ground state. Around the peak of pulse, the LG curve shows most dramatic oscillation in survival. The KH frame gives the smoothest curve. However, all three gauges are converged to the same survival and depletion. When much stronger laser field (1×1018 W/cm2) is applied, in the three graphs of right panels, we observe completely depletion of ground state in the LG curve around the peak of pulse. The VG curve also shows strong oscillation in the survival. While the KH frame result again has the smoothest survival curve. And all results from three gauges are the same at the end of pulses.
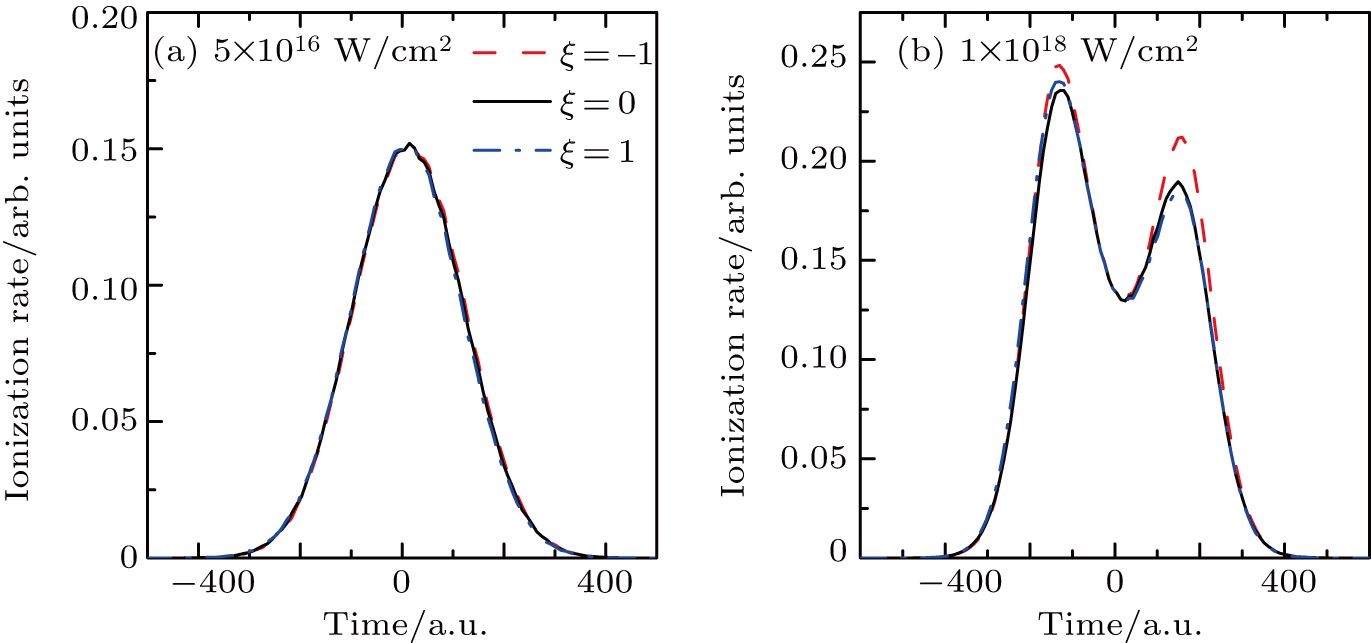
In Fig. 3, the photoelectron spectra (PES) are displayed. As we can see in Fig. 3, the curves of VG in Figs. 3(a) and 3(b), the curves of LG in Figs. 3(c) and 3(d) and the curves of KH in Figs. 3(e) and 3(f) are in pretty good agreement with each other, which is an indication of convergence of our simulations. It is surprisingly that the photoelectron energy spectrums are almost identical for three gauges above, although the survival curves show obvious difference each other. It agrees with the physical requirement that observable variables are not dependent on the choice of gauges. The top panels are for 6-fs pulses with laser peak intensity 5.0×1016 W/cm2, that is about 1 atomic unit (3.51×1016 W/cm2) of laser intensity. For high frequency laser pulse, its photoelectron spectra can be obtained by the lowest order perturbation theory (LOPT). In this case, there is no multi-fringe structure can be observed for all three gauges, which means there is no obvious dynamic interference with such intense laser field with only 6-fs pulse duration. The photoelectron spectra of chirped and chirp-free pulses with this intensity are very similar to the power spectral profiles of laser pulses, respectively. It is in good agreement with the LOPT prediction. On the bottom panels, when we increase the laser peak intensity to 1.0×1018 W/cm2, all curves with different gauges display strong interference fringes. Compared to the chirp-free black solid curves, the chirped curves (red dashed and blue dotted-dashed curves) basically repeat the black curves at the high energy end of photoelectron spectra, but show significant discrepancies on the low energy end of photoelectron spectra. As displayed in Figs. 1(a) and 4(b), the chirped and chirp-free pulses have the same FWHM and similar time intervals for the two wave-packets generated from the rising and the falling edges of chirped pulses. The interference fringes dependent on the phase difference of rising and falling wave-packets, which is mostly attributed to the time interval of those wave-packets and field intensity.[13] Therefore they give similar photoelectron spectra.
When we look into the time-dependent ionization rate of the hydrogen atoms in Fig. 4, we can better understand this interference in two cases. In Fig. 4(a), with lower laser intensity, the max ionization happen at t = 0, so it is hard to observe obvious interference fringes. When the laser intensity is increased to much stronger such as 1.0×1018 W/cm2 in Fig. 4(b), we can find two well separated photoelectron wavepackets from ascending and descending edges of laser envelop, respectively. The birth times for them are
 for all different chirps. The photoelectron wavepackets from the first and second halves of laser envelop will interfere each other and give interference fringes. The chirped pulses have very similar time-dependent ionization rate curves, and the birth time tb are almost the same as chirp-free case. Since the chirped and chirp-free pulses have same envelop and FWHM, the atomic stabilization effect are almost the same for them. Therefore the time-dependent ionization rate are similar in all three different chirps.
for all different chirps. The photoelectron wavepackets from the first and second halves of laser envelop will interfere each other and give interference fringes. The chirped pulses have very similar time-dependent ionization rate curves, and the birth time tb are almost the same as chirp-free case. Since the chirped and chirp-free pulses have same envelop and FWHM, the atomic stabilization effect are almost the same for them. Therefore the time-dependent ionization rate are similar in all three different chirps.
In Fig. 5, we increase the pulse duration to 30 fs, and keep the other parameters the same as Fig. 3. Again we notice that all gauges produced nearly identical results. Compare with the results of short pulse (6 fs) in Fig. 3, we can observe more typical features for the long pulse duration (30 fs) with either weaker 5.0×1016 W/cm2 or stronger 1.0×1018 W/cm2 laser intensities in Fig. 5. The dynamic interference can now be observed even in the weaker 5.0×1016 W/cm2 which does not shown in a short period. And at peak strength of 1.0×1018 W/cm2, the number of fringes of the first ATI peak is larger and the interference effect is dominant. The increasing in number of fringe numbers with higher laser intensity and longer pulse duration is due to the increasing in the phase difference of photoelectron wavepackets from ascending and descending envelop of laser pulses.[13] After applying chirp to a pulse, we can also observe weakening fringes in the lower energy end of photoelectron spectra. While at the high energy end of photoelectron spectra, especially for the strong laser intensity, the fringes of photoelectron spectra has little changes for different chirps. It is similar to the short-pulse case, the chirped and chirp-free pulses have the same full width at half maximum. So all pulses have similar time intervals (Fig. 4(b)) for the two wave-packets generated from the rising and the falling edges of chirped pulses. Therefore they give similar photoelectron spectra. In addition, from Eq. (7), we know that the increase in pulse duration leads to smaller frequency changes. It is also the reason of similar photoelectron spectrum with or without chirp.
For the short (6 fs) and long (30 fs) laser pulses of Figs. 3 and 5 respectively, we observe different changes with different chirped pulses. In the 6-fs pulse, after applying chirp, the highest peak and high energy end of photoelectron spectra shift up, while for the 30-fs pulse there are almost no changes in the high energy end. To investigate the trend of the dynamic interference on the changing of chirp parameter ξ, in Fig. 6, we calculated photoelectron spectra with different chirped pulses. Due to the similarity in photoelectron spectra of positive and negative chirped pulses, only positive chirps are shown. We increased the chirp parameter from chirp-free ξ = 0 to ξ = 1, 2, and 3. As the chirp increases, the photoelectron spectra are broaden and the fringes of interference will be gradually vanished. When ξ = 3, it is hard to observe fringes for 6-fs pulses. Besides, it is also notable that the peak position of each curve shift to right compared to chirp-free curve for curves of 6-fs pulses, but not change in curves of 30-fs pulses. In Figs. 6(c) and 6(d), we plot the spectral profiles of each pulses. To keep the same full width at half maximum as chirp-free pulse, the chirped pulses have wider power spectral profiles than chirp-free pulses. In the LOPT, the expansion in the spectral will give broaden photoelectron spectra. This is in agreement with the photoelectron spectra here.
To understanding the disappearing of dynamic interference fringes and red shift of peak positions, we need to look back to the original of dynamic interference effect. As discussed in previous studies by Demekhin et al.,[16] Bahgary et al.,[17] and Jiang et al.,[13] the occurrence of dynamic interference requires both rising of energy level by ac Stark shift with strong laser pulses. And what is more important, the stabilization of atomic system in super-intense laser field, which can assure the interference by electron wave-packets from both ascending and descending halves of laser envelop.[13] When there is no chirp added to laser pulses, due to the atomic stabilization effect, we assume the maxima ionized electron wave-packets are generated at ±t1,[13,16] and they have equal kinematic energy
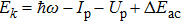 . Here, Ip = 13.605 eV is the ionization potential of hydrogen atom. The term
. Here, Ip = 13.605 eV is the ionization potential of hydrogen atom. The term
 is the pondermotive quiver energy of laser field, and
is the pondermotive quiver energy of laser field, and
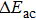 is the instantaneous cycle-average ac Stark shift of ground state in laser field. These two terms account for the energy shift up (∼0.3 eV for I0 = 5×1016 W/cm2 with
is the instantaneous cycle-average ac Stark shift of ground state in laser field. These two terms account for the energy shift up (∼0.3 eV for I0 = 5×1016 W/cm2 with
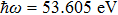 central frequency laser pulse) from
central frequency laser pulse) from
 , as indicated in figures. When applying chirped pulses, the instantaneous frequency is changing with time, as shown in Fig. 3(c). For instance, in ξ = 1 case, the instantaneous frequency at
, as indicated in figures. When applying chirped pulses, the instantaneous frequency is changing with time, as shown in Fig. 3(c). For instance, in ξ = 1 case, the instantaneous frequency at
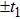 is
is
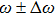 , the term
, the term
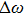 is the discrepancy between the time
is the discrepancy between the time
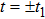 and t = 0. Therefore, at the maxima ionization times
and t = 0. Therefore, at the maxima ionization times
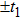 with chirped pulses (as shown in Fig. 4, t1 is unchanged), the final kinematic energy will be different with
with chirped pulses (as shown in Fig. 4, t1 is unchanged), the final kinematic energy will be different with
 . This mismatch in final kinematic energy of photoelectrons means the loss of interference. The larger is the
. This mismatch in final kinematic energy of photoelectrons means the loss of interference. The larger is the
 , the weaker interference patterns are expected. So when we increase the chirp parameter ξ, the interference fringes will be weaken or disappear.
, the weaker interference patterns are expected. So when we increase the chirp parameter ξ, the interference fringes will be weaken or disappear.
4. ConclusionThe TDSE has been numerically solved under different gauges (LG, VG, and KH) for the interaction between the ground state hydrogen atoms and ultrashort super-intense laser pulses. Our investigation on the PES of hydrogen atoms with chirp-free super-intense ultrafast pulses is in agreement with Guo et al.,[12] and Jiang et al.[13] Different from the chirp-free case, in the presence of a super-intense chirped laser pulse, we find that: (i) by adding chirp, the dynamic interference effect will be weaken for weak and short pulses; (ii) due to the wider spectral profile of chirped pulses, the PES also become wider. (iii) But it is not obviously for long and intense chirped pulses, where the PES significantly suppressed at lower energy end and almost unchanged in high energy end.