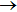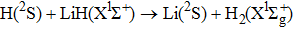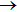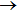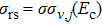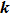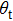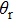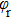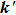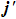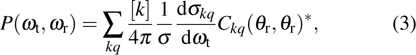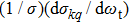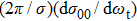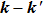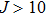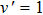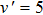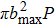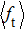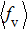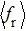1. IntroductionIn the past decade, the lithium chemistry in the early universe, involving the collision between H atom and LiH, has been the subject of many theoretical and experimental investigations.[1–9] Observations the origin of cosmic background radiation and anomalous microwave emission along the line of sight of young stars have provided rich information about the physical conditions in which molecules are first formed, then excited and finally destroyed.[2–5] Generally, molecular formation in the early universe began when the temperature was low enough that the newly formed atoms could survive for further evolution. The large permanent dipole moment and the light masses of LiH molecule make it a potential target in these molecules. Therefore, the existence of LiH and its ionic counterparts may cause significant anisotropy of the cosmic background radiation. Based on these considerations, the formation and depletion of LiH molecule is considered to be a crucial subject in galactic lithium and stellar evolution.[1,2] Especially from the point view of primordial universe models, the depletion of LiH appears to be much more important than the formation.[4–6,8] On the energy transformation side, the H+LiH reaction, which is found to be highly exothermic about 2 eV and barrierless along the reaction path.[10–16] The increase of interest in the LiH2 system may be related to several factors. First, the number of electrons is five, two of which are core electrons of Li atom and three are valence electrons that involved in the ground state. It is tractable to carry out accurate computations. Second, H+LiH reaction is generally regarded as the simplest triatomic reaction system involving an alkali metal atom,[15] the alkali metal atoms present a high density of nearby excited electronic states into which they can be easily promoted. This allows nonadiabatic transitions to take place.
Because of the astrophysical importance of H+LiH reaction, a great deal of effort has been made to uncover the reaction dynamics and kinetics since the early days of this research. This also promotes the development of potential energy surface (PES), which is the precondition to study reaction dynamics. In 1998, an adiabatic PES was developed for collinear arrangements with spin-coupled valence bond (SCVB) non-orthogonal configuration interaction (CI) method by Clarke et al.,[17] and a small barrier of 0.036 eV and a strong exothermicity of 2.0238 eV were found for the depletion channel H+LiH
Li+H2. Later on, a series of three-dimensional PESs[12,14–16,18] was constructed with the aim to investigate the reactive processes. In 2001, Dunne et al.[12] developed the first three-dimensional PES (denoted as DMJ PES) for LiH2 system in its ground electronic state by fitting a many-body potential to energies from high quality CI ab initio calculations. They found no barrier to the depletion reaction, in contrast with the Clarke PES. However, the DMJ PES holds unphysical wells at the H–LiH and Li–H2 valleys. Subsequently, Padmanaban and Mahapatra[19–22] and Defazio et al.[23] carried out quantum calculations based on this DMJ PES. Their results show that the
Li+H exchange reaction is the dominated process. After two years, Kim et al.[14] calculated an accurate PES at the multi-reference configuration interaction (MRCI) level and interpolated by the interpolant moving least squares (IMLS)/Shepard scheme. Meanwhile, the work also reported trajectory calculations for Li+H2 reaction to test the quality of the PES, in which the dynamics results were compared with that of Dunne et al.[12] Recently, Wernli et al.[15] presented a PES (denoted as WCBG PES) for the electronic ground state with a complete active space self-consistent field (CASSCF) method and an MRCI treatment of the correlation energy. In the same year, Prudente et al.[16] proposed a new PES (denoted as PMM PES) for LiH2 by full configuration interaction (FCI) method and an aug-cc-pVQZ basis set. The PMM PES shows a small early-staged energy barrier, but no unphysical well in contrast with DMJ PES. Just recently, Yuan et al.[24] developed a new global PES (YHC PES) for the ground electronic state of LiH2 with the neural network (NN) method at MRCI level. The spectroscopic constants were found to fairly consist with the experimental date.
Extensive quantum mechanical (QM)[16,25–31] and quasi-classical trajectory (QCT)[32–39] dynamics studies have been carried out on the recently developed PESs.[15,16] The WCBG[15] and PMM[16] PESs are both attractive along the minimum energy path of the title reaction. The reaction probabilities and integral cross sections (ICSs) for the total angular momentum J = 0 obtained with quantum methods showed that the depletion reaction dominates over the exchange reaction.[16,25–29] The calculated ICSs show no threshold and decrease with collision energy, as expect for a typical barrierless reaction. Meanwhile, the QCT calculations were also performed and drew the same conclusion.[37,39] Differential cross section (DCS) or polarization dependent DCS plays a key role in understanding the reaction mechanism fully. Thus several studies focused on this point, and the results displayed a forward scattering of H2 molecules.[30,32,34–36,38] The intensity of sideward and backward scatterings decreases with increasing collision energy.
The characters of PES govern the reaction dynamics. The fitting procedure of WCGB PES seems to be better than that of PMM PES, and the latter PES presents a small barrier of about 0.05 eV, which is absent in the former PES. Because of the difference between WCBG and PMM PESs, dynamics calculations may present different physical pictures. With the aim to get more accurate dynamics results, the YHC PES was reported with NN method.[19] The root mean square error is very small (0.004 eV), and is smaller than that of PMM PES. The YHC PES also confirmed the absence of energy barrier on the minimum energy path (MEP). Meanwhile, the time-dependent wave packet (TDWP) calculations were performed to investigate the dynamics of the reaction
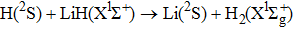on the YHC PES.[24] The results are somewhat different from those on PMM and WCBG PESs. To the best of our knowledge, QCT calculations of H+LiH
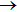Li+H2 on the new YHC PES have not been reported so far. As a supplement of QM calculations, QCT calculations offer an interesting choice to probe the reaction dynamics intuitively.
In this work, we performed a detailed QCT study of the title reaction on the new lowest doublet state of LiH2 system.[24] Reaction probabilities for different J values and ICSs are compared with QM results. The influence of initial vibrational excitation of reactant on dynamics is also studied. The rest of paper is structured as follows. In Section 2, features about the PES used and details of calculations are outlined. In Section 3, we present the results and discussion. Section 4 draws a conclusion.
2. General theory2.1. Potential energy surfaceIn addition to the aug-cc-pVXZ (X = Q, 5) basis sets used, the NN method has been used to construct the high-quality PES.[24] The spectroscopic constants of LiH and H2 are found to be in good agreement with experimental data. At four different Li–H–H angles (180°, 135°, 90°, and 45°), the PESs are smooth over the whole configuration space and they confirm the absence of barrier or well along the reaction paths, which is similar to the WCBG PES. The features suggested that there is no energy threshold for reaction probabilities and fewer resonance structures are expected to be observed. When the H atom moves around the fixed LiH molecule, the potential energy supports a deep well around the fixed H atom. This deep well may take responsibility for the attractive feature of the PES and the stripping mechanism of the collision process.
2.2. Quasi-classical trajectory methodSince the standard quasi-classical trajectory methodology adopted here has been extensively described elsewhere,[40–45] only the computational details will be given here. The QCT calculations were performed for the reaction H+LiH (v = 0, 1, 2, j = 0)
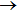Li+H2 in the collision energy 0 eV–0.5 eV. The trajectory was started at a distance of 10 Å between the attack atom H and the center-of-mass of the LiH molecule. This distance ensures a negligible initial interaction between them. The time step size was chosen to be 0.1 fs for the integration of the equations of motion, which is sufficiently small to guarantee the conservation of total energy and total angular momentum. A batch of 2×105 trajectories was run at every collision energy Ec. The impact parameter b of trajectory for different J values can be obtained using the expression[46]
where
μ is the H–LiH reduced mass,
v and
L (
L =
J when
j = 0) are the relative velocity and the orbital angular momentum quantum number, respectively. The maximum impact parameter
bmax is large enough that no reactive trajectories can be observed with
.
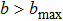
For J = 0 and b = 0, the reaction probability was obtained by
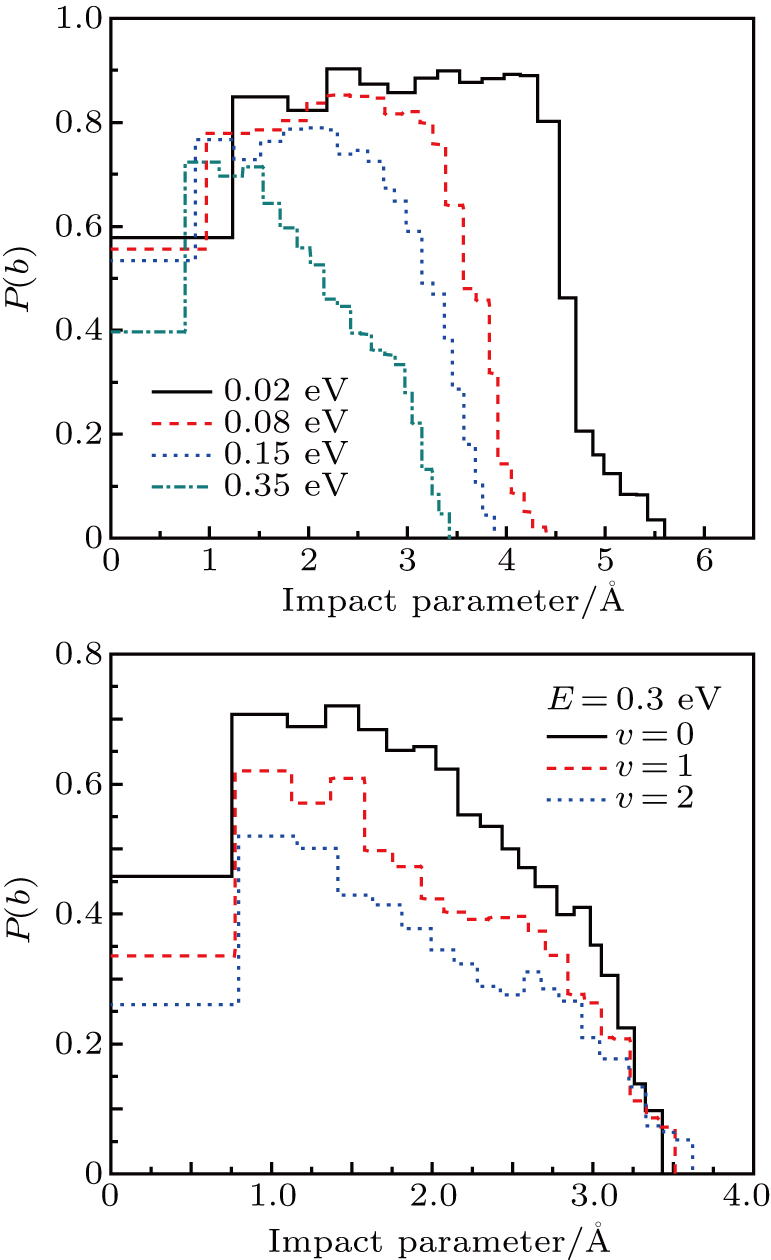
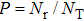, where Nr and NT denote the numbers of reactive and total trajectories. Next, the integral cross section is defined as
The sampling error of ICS is defined as
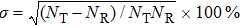, and the statistical uncertainty as
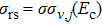. In the calculations, the reactive trajectories with the final quantum number smaller than zero were discarded.
To describe the scattering direction of product molecule, the center-of-mass (CM) frame is adopted. In the CM frame, the reagent relative velocity vector
is parallel to the z axis while the y axis is perpendicular to the x–z plane containing the initial and final relative velocity vectors,
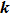and
.
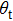is the so-called scattering angle between the reagent relative velocity and the product relative velocity, while
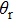and
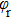refer to the coordinates of the unit vectors
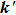and
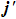along the directions of the product relative velocity and rotational angular momentum vectors.
The fully correlated CM angular distribution can be written as[47–49]
where
Ckq represents the modified spherical harmonics, and
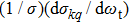
the generalized polarization-dependent differential cross-section (PDDCS). In the present work, we calculate
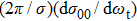
, which is a simple differential cross-section (DCS) describing only the
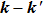
correlation or the scattering direction of the product.
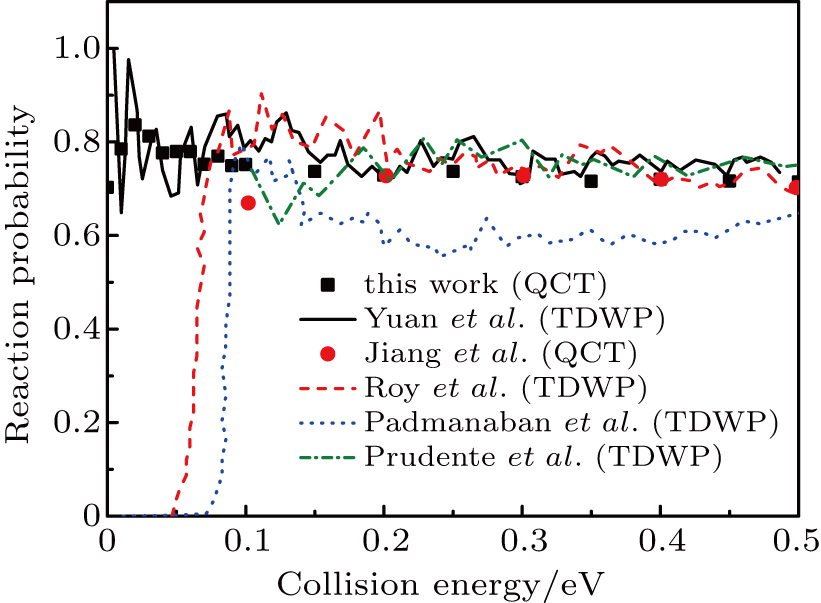
3. Results and discussion3.1. Probability and cross sectionConsidering the first QCT calculations of H+LiH reaction on the new PES,[24] we compared the present QCT probabilities for H+LiH (v = 0, j = 0)
Li+H2 with the available theoretical results[16,19,24,27,36] achieved on the other three PESs[12,16,17] in Fig. 1 to verify the validity of QCT calculations. Although the quantum results on YHC PES represent some resonance structures at low collision energies,[24] however, the present QCT results well-reproduce the quantum curve on the whole, which indicates the reliability of QCT treatment of LiH2 system on this PES. Note that the present QCT results, in the whole energy range, are somewhat smaller than the corresponding QM results[24] on the YHC PES. This may be related to the fact of the absence of the quantum effect in QCT calculations. Significant differences were observed between the results on the YHC PES and other ones[19,27,36] in low energy region, which can be attributed to the characters of different PESs. For example, the calculations of Ref. [19] employed the DMJ PES, which presents unphysical wells in the Li–H2 and H–LiH asymptotic valleys. The PMM PES exists an early-staged barrier about 2.14 kcal/mole at the collinear arrangement, which is not found on the WCBG PES and YHC PES.
The ICSs for the reaction as a function of collision energy are shown in Fig. 2. Clearly, the agreement between present QCT results and QM results[24] on YHC PES is fairly good, except in very low collision energy region where resonances are dominated. Similar to the reaction probability in Fig. 1, the remarkable differences between results on YHC PES and other theoretical results[21,27,30] were observed, at collision energies lower than 0.05 eV. This phenomenon can be explained by the fact that the YHC PES is much more attractive than the WCBG and DMJ PESs leading to a precipitous rise for the ICS in low energy region. The ICSs decrease from a high value with increasing the collision energy, as expected for a barrierless exothermic reaction. This behavior is in clear agreement with the TDWP calculations[24] which is also found in reaction H+Li2
LiH + Li.[50] Below the energy of 0.05 eV, the ICSs rapidly increase to values in the range 40 Å2–110 Å2. Thus, most of the reactivity for this system happens at low collision energies.
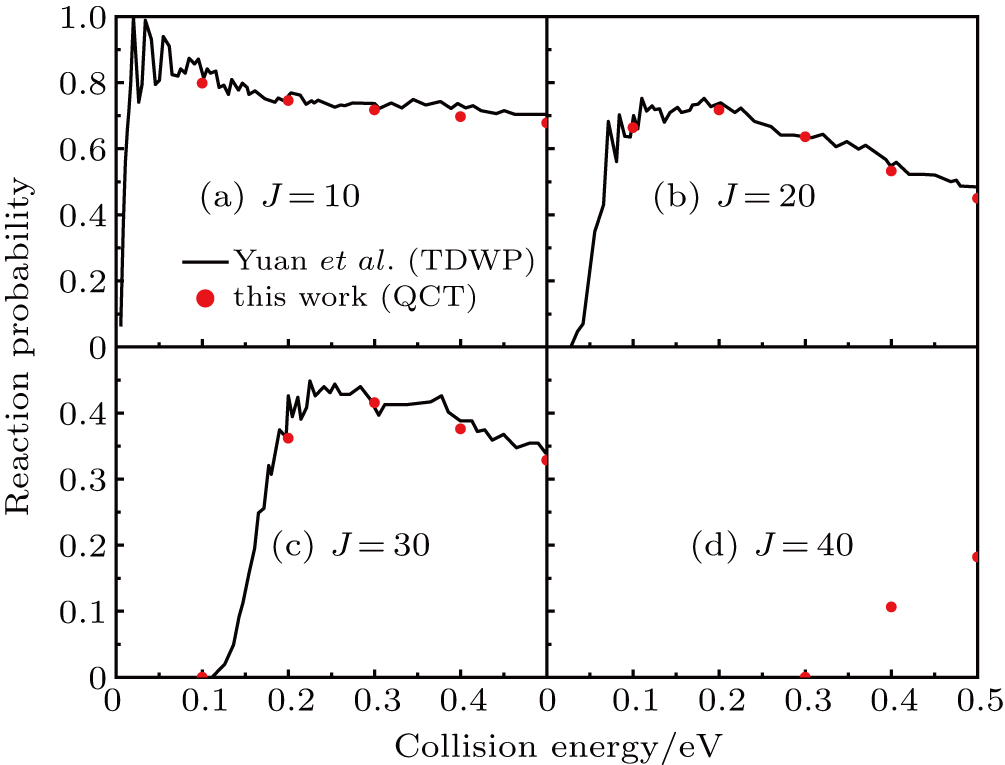
The reaction probabilities as a function of collision energy at selected J values are shown in Fig. 3. The present QCT results are in good agreement with the QM results reported in Ref. [24]. It is clearly shown that there is no energy threshold for J = 10, while for
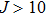the energy threshold appears. In addition, the energy threshold shifts to higher with the increasing of J, due to the centrifugal barrier. The overall reaction probability decreases with the increasing of J. For example, at 0.4 eV, probabilities for J = 10, 20, 30, 40 are 0.69, 0.53, 0.37, and 0.11, respectively.
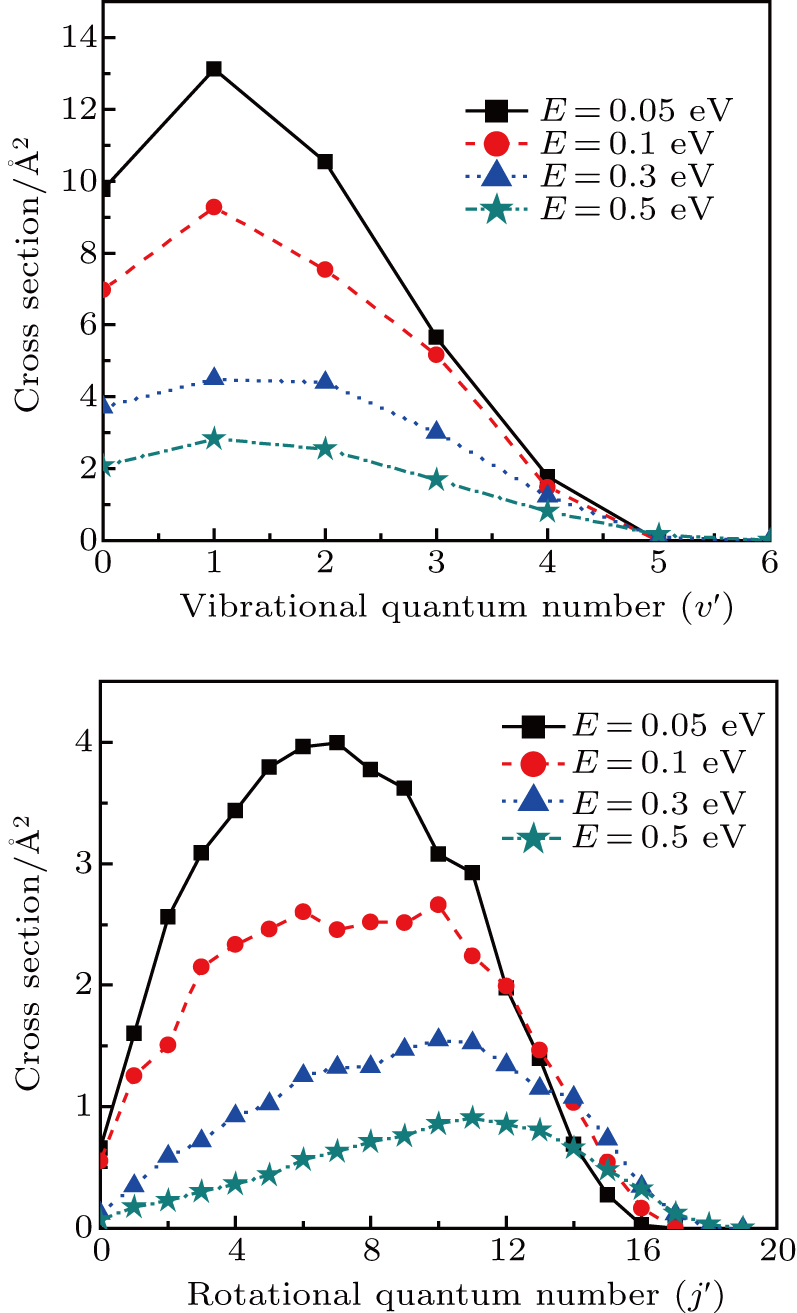
3.2. Rovibrational state and energy distributions of productThe product rovibrational state distributions at several selected collision energies are shown in Fig. 4, which sum all rotational state populations and vibrational state populations corresponding to each vibrational and rotational channel. One can see that the H2 products are formed either vibrationally or rotationally excited. The vibrational distributions of upper panel show that the H2 molecules are mainly formed in relatively low vibrational states
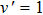at collision energies marked. The maximum of quantum number is about
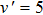for the four collision energy energies. With the increase of energies, the shape of vibrational distributions becomes broader and smoother, and the distributions monotonically decrease. This phenomenon is consistent with the energy dependence of ICSs shown above as well as the character of the stripping mechanism. However, the effect of collision energy on the opening of vibrational channels is very small. The product rotational distributions are displayed in the lower panel. Bell-shaped curves can be observed for the four selected collision energies. The peaks of rotational distributions reduce and shift to higher
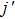values with increasing collision energy. Meanwhile, more rotational channels open with rotational quantum number from
up to
.
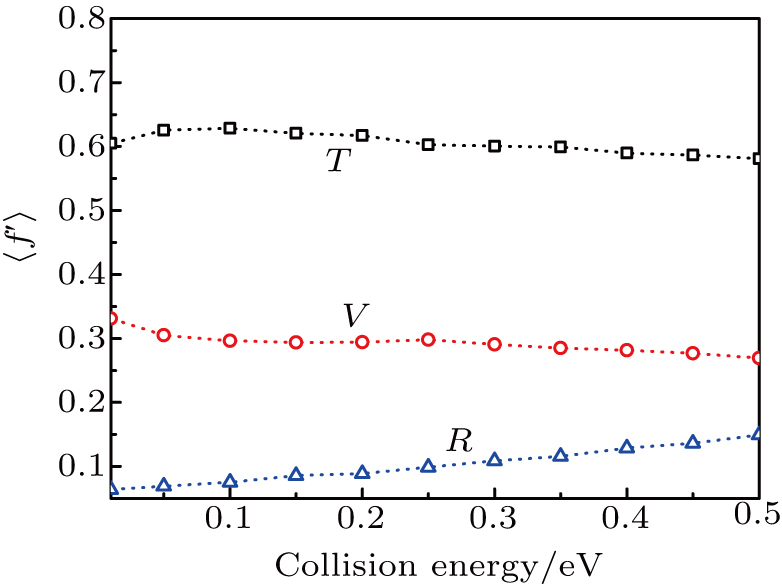
As a key question in reaction dynamics, product energy distributions have been discussed in detail.[51–53] Generally, product energy distributions are sensitive to the different mass combinations and characters of potential energy surface. In Fig. 5, we display the final energy proportions of the product between translational, vibrational and rotational motions (fT, fV, and fR, respectively) as function of collision energy. Note that a large proportion about 60% of the total energy is released as translation energy of product. As collision energy increases, the proportion of translational energy shows a slight increase and then a gradual decrease. By contrast, the proportions of rotational energy and vibrational energy present a distinct increase and decrease with collision energy. For an attractive PES and
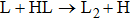(where L and H denote light and heavy atoms) reaction, it appears that the majority of available energy would be partitioned into translational energy of product.
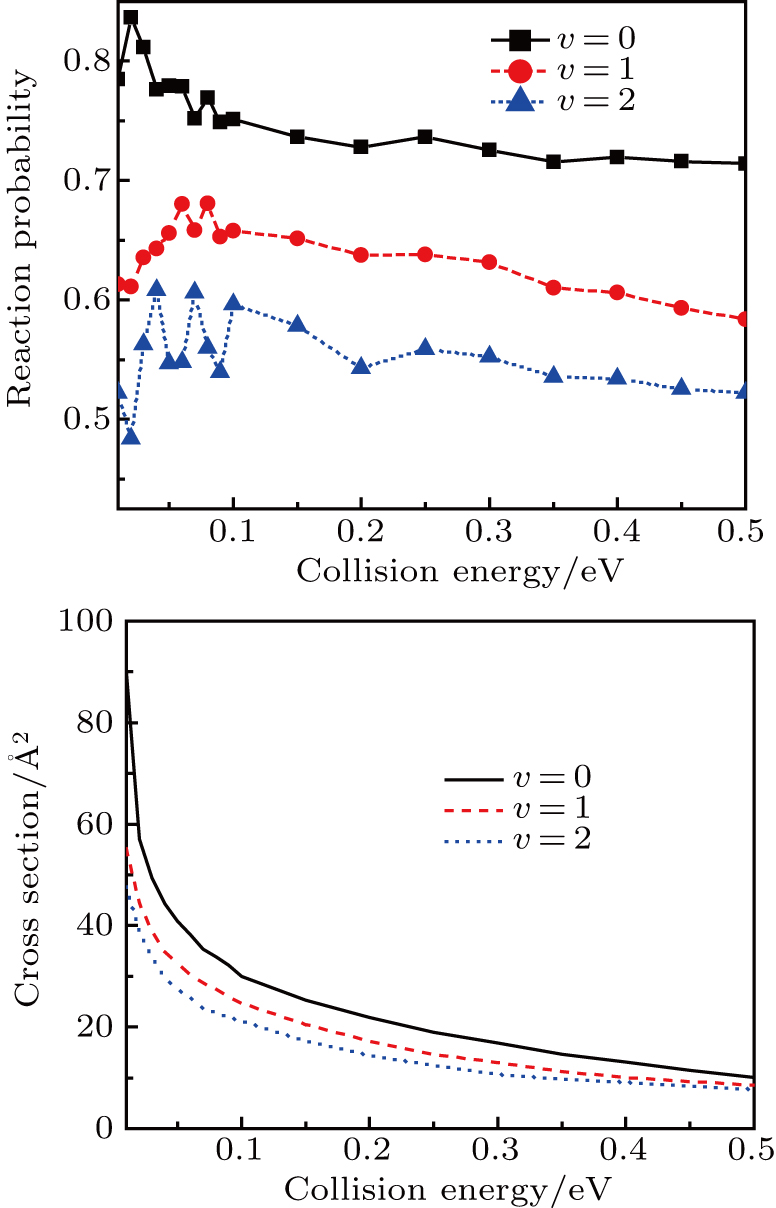
3.3. Reactant vibrational excitationIt is interesting to examine the effect of reactant vibrational excitation on the reactivity, which could provide more information of reaction process. The J = 0 reaction probabilities and ICSs for LiH (v = 0–2) as a function of collision energy are plotted in Fig. 6. It is clear that the vibrational excitation of the reactant molecule LiH has a negative effect on both the probabilities and ICSs, which has also been found in the previous works.[27,29,30,37,38] This phenomenon can be attributed to two factors. On the one hand, the attractive PES employed, which shows no barrier in the reactant and product channel, results in the ineffectiveness of reactant vibration in promoting the reactivity. On the other hand, the H atom is lighter than Li atom, thus the vibration of LiH molecule does not favor on the formation of H2 molecule, which leads to the reduction of H2 formation. It seems that at low collision energies the effect of vibrational excitation is more distinct. As collision energy increases, the ICSs for different vibrational quantum number tend to be identical.
To get an initial understanding of the reactivity of the title reaction, the opacity function or reaction probability P(b), i.e., the fraction of collisions with impact parameter that leads to reactions, is necessarily calculated and depicted in Fig. 7. P(b) ranges from 0 to 1. Note that the opacity function is sensitive to the collision energy and initial vibrational excitation. It tends to sharply increase and then monotonically decrease to zero at bmax. As shown in the top panel, the probabilities with the same impact parameter are suppressed when collision energy increase. As collision energy increase, the maximum of the impact parameter ends up with a smaller value. That is, the reaction with larger b appears to be more evident at lower collision energies. Such behavior will have a considerable influence on the ICSs because they are determined by
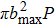. As known, the height of the centrifugal barrier is in proportion to collision energy for a given b, it is easy to understand the decrease in bmax as collision energy increases. The shape of the opacity functions in the bottom panel shows a similar behavior with the initial vibrational excitation on the whole, which is consistent with the conclusions in Fig. 6. The range of impact parameters presents a slight enlargement when the reactant is vibrationally excited to high levels.
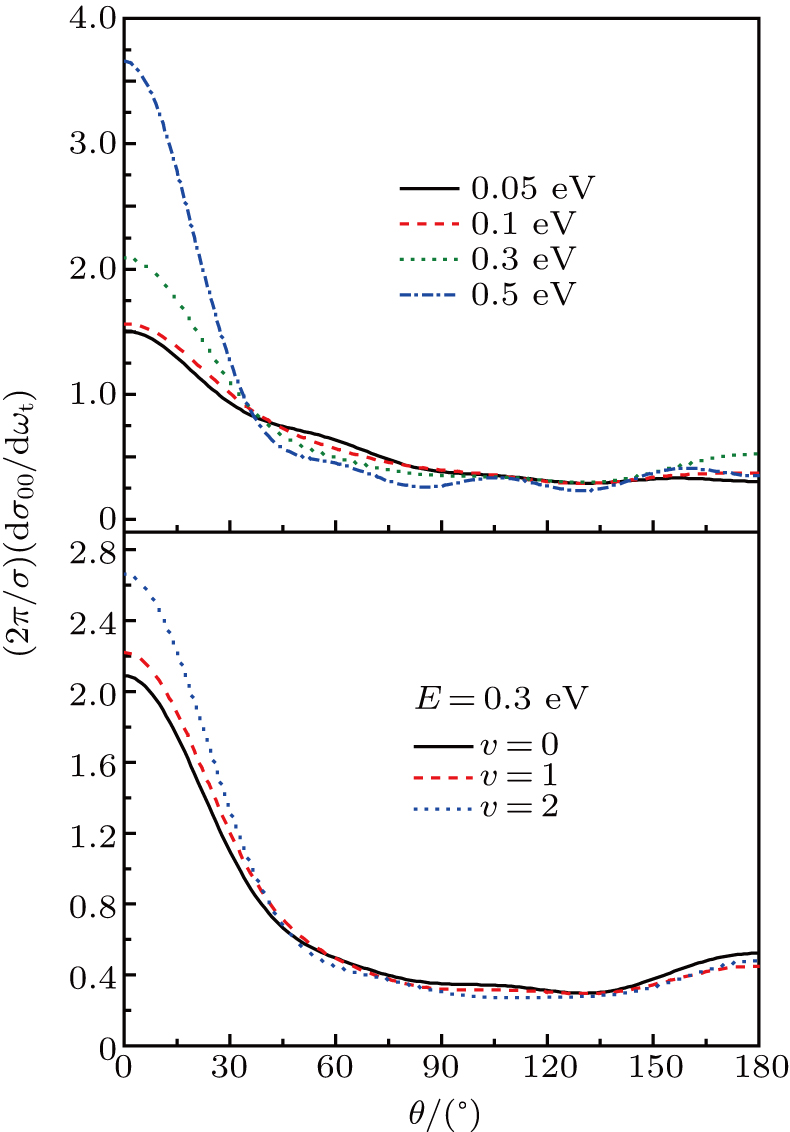
It is of interest to investigate the direction of the product, which could offer rich dynamics of reaction. The polarization dependent DCS
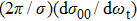, which describes the correlation between the reactant and product relative velocity (i.e., the distributions of DCSs) is shown in Fig. 8. The top panel shows the DCSs at four selected collision energies. Clearly, the product forward scattering direction of θ = 0° is favored in all cases. The intensity of forward scattering becomes stronger with increasing the collision energy, and the scattering angles are restricted in the range 0°∼90°. As stated above, the domination of stripping reactive trajectories in the reaction with the increase of collision energy may contribute to the preference of the forward scattering peak. Furthermore, for a light–heavy–light mass combination system, the product would prefer to display a forward scattering at high collision energies on an attractive PES.[41] In order to get more insight into the reaction, we also investigate the effect of reactant vibrational excitation on the product scattering. The bottom panel shows DCSs at a specific energy for vibrational excited LiH (v = 0, 1, 2 and j = 0). Interestingly, the collision energy and vibrational excitation of reactant affect the DCSs in a similar way. With the reactant LiH being excited to higher levels, the product molecule H2 represents a stronger forward scattering.
3.4. Reaction mechanismTo get a better understanding of the reaction mechanisms, we illustrate two reactive trajectories at collision energy of 0.1 eV in Fig. 9. Figures 9(a) and 9(b) represent stripping and indirect reactive trajectories respectively. This supplies the evidence of the two distinct reactive mechanisms in the reaction. In Fig. 9(a), the
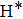atom goes through 420 fs, and collides directly with H atom of target molecule. After the impact, the product
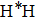forms and keep going to the origin direction immediately. This is the typical stripping mechanism in a direct reaction. However, we also observe some long lived trajectories, namely “trapped” trajectories, especially in relatively low collision energies. In Fig. 9(b) the LiH molecule gets excited after a collision, and the remaining translation energy is not enough to support its dissociation. Thus the reaction system flies back to collide again, after arriving at the outer classical turning point. This process repeats several times until the system accumulates enough translation energy to dissociate in the possible channels. The reaction time is longer than 2500 fs. This trajectory reveals the indirect reactive mechanism in the reaction. However, after the statistics of the trajectories, we found that the number of indirect reactive trajectories reduces sharply with the increase of collision energy.
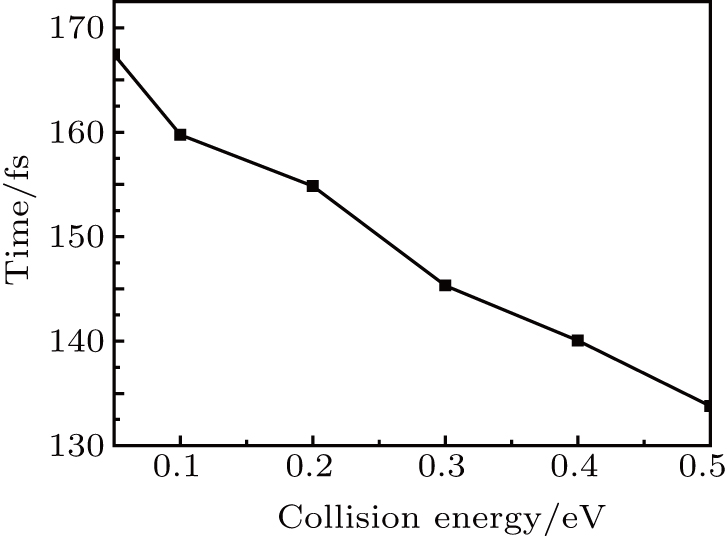
As a supplement to the above conclusions, the average lifetime of intermediate complex is shown in Fig. 10. The traditional method is employed to definite the lifetime of the complex-forming.[54] It is clear from the figure that the average lifetimes of the complexes decrease with the collision energy increase. This phenomenon can be attributed to the fact that the reaction is mainly dominated by the stripping reaction mechanism at high collision energies, whereas indirect reaction mechanism plays a role at low collision energies.
4. ConclusionsIn conclusion, the dynamics of the H+LiH (v = 0–2, j = 0)
Li+H2 reaction has been investigated in detail on a new ground potential energy surface by means of QCT method. The reaction probabilities and ICSs determined up to 0.5 eV are found in good agreement with QM results, which verifies the accuracy of present QCT treatment. The ICSs show no threshold and sharply decrease at low collision energies, whereas the results relatively smoothly decrease at higher collision energies, as expected for a barrierless entrance channel. The initial vibrational excitation of reactant inhibits the reactivity because of the attractive property of the PES. The polarization dependent DCSs suggest that the products are predominantly forward scattered due to the domination of stripping mechanism. However, indirect mechanism also exists, especially at low collision energies.
