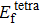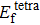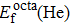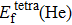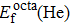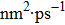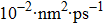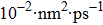Cite this Article
Liu Zhi-Yong, He Bin, Qu Xin, Niu Li-Bo, Li Ru-Song, Wang Fei. Energetics and diffusion of point defects in Au/Ag metals: A molecular dynamics study. Chinese Physics B, 2019, 28(8): 083401  
Permissions
Energetics and diffusion of point defects in Au/Ag metals: A molecular dynamics study
Liu Zhi-Yong, He Bin, Qu Xin, Niu Li-Bo, Li Ru-Song †, Wang Fei ‡
Xi’an High Technology Institute, Xi’an 710025, China

 

† Corresponding author. E-mail: rusong231@126.com wf285352065@sina.com

Abstract

To reveal the potential aging mechanism for self-irradiation in Pu–Ga alloy, we choose Au–Ag alloy as its substitutional material in terms of its mass density and lattice structure. As a first step for understanding the microscopic behavior of point defects in Au–Ag alloy, we perform a molecular dynamics (MD) simulation on energetics and diffusion of point defects in Au and Ag metal. Our results indicate that the octahedral self-interstitial atom (SIA) is more stable than the tetrahedral SIA. The stability sequence of point defects for He atom in Au/Ag is: substitutional site octahedral interstitial site tetrahedral interstitial site. The He–V cluster ( , V denotes vacancy) is the most stable at n = m. For the mono-vacancy diffusion, the MD calculation shows that the first nearest neighbour (1NN) site is the most favorable site on the basis of the nudged elastic band (NEB) calculation, which is in agreement with previous experimental data. There are two peaks for the second nearest neighbour (2NN) and the third nearest neighbour (3NN) diffusion curve in octahedral interstitial site for He atom, indicating that the 2NN and 3NN diffusion for octahedral SIA would undergo an intermediate defect structure similar to the 1NN site. The 3NN diffusion for the tetrahedral SIA and He atom would undergo an intermediate site in analogy to its initial structure. For diffusion of point defects, the vacancy, SIA, He atom and He–V cluster may have an analogous effect on the diffusion velocity in Ag.

PACS: 34.20.Cf;61.80.-x;61.72.-y;36.40.Sx
Keyword:interatomic potential;radiation damage;point defect;diffusion barrier
1. Introduction

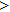
Over the past few years, we have witnessed great progress of nucleation and growth mechanisms for He behavior in Pu-based materials, in particular pure δ phase Pu and Pu–Ga alloy.[1–9] As a radioactive nuclide, Pu α decay would produce various defects, such as He interstitial atom, self-interstitial atom (SIA), and vacancy, result in a collision displacement cascade, and disrupt the physical, chemical and mechanical properties of Pu-based system. Therefore, the self-irradiation effect, in particular He–V (V denotes vacancy) cluster, would be useful for revealing the aging mechanisms in Pu-based materials. However, we have not yet completely understood the self-irradiation effect in Pu material, in particular the aggregation of He atoms, the nucleation and growth of He–vacancy cluster and/or He bubble, which still need further investigation.[10] Recently, many research groups[11–14] have done a lot of excellent work on the electronic, magnetic and structural properties of metallic Pu and its alloys, 5f itinerant/localized behavior, superconductivity and collision displacement cascade induced by self-irradiation in Pu-based materials by using multi-scale simulation technique, such as first principle, molecular dynamics and kinetic Monte Carlo. However, the low symmetry for ground state of metallic Pu (i.e., α phase Pu), the relativistic effect resulting from high atomic number of Pu and the strongly correlated effect arising from the partially filled Pu 5f orbitals pose a considerable challenge for condensed matter physics.

In fact, the theoretical research on the physical, chemical and mechanical properties of He atom in δ-Pu is very difficult to perform due to the δ-Pu having chemical activity, toxicity, radioactivity, complex 5f occupation, and metastable phase stability, which is extremely sensitive to temperature, pressure and chemical doping. Therefore, experimental observation and/or numerical simulation on a substitution material for Pu–Ga alloy can be a feasible approach. In principle, self-irradiation effect induced by 239Pu α decay is dependent on the lattice structure and mass density, thus we consider Au–Ag alloy (fcc structure) to be an apposite substitution for Pu–Ga alloy (fcc structure). In this respect, the physical properties, point defect properties and He behavior in Au–Ag alloy can be useful for understanding the He behavior in Pu–Ga alloy. Stevens et al.[15] have used a transmission electron microscope (TEM) to investigate the nucleation and growth of He defects in Au–Ag alloy, and found that He bubbles are non-uniformly distributed across the crystal lattice, and the nucleation of He bubble might not be related to He irradiation in Au–Ag alloy. For He behavior in Au–Ag alloy, Thomé et al.[16] have investigated the radiation damage to He implanted Au-based alloy (Au3Ag2) by using the positron annihilation spectrum (PAS) technique. Their results indicate that a fundamental reason for the degradation of Au3Ag2 alloy is pressure increase resulting from the nucleation and growth of He bubble. Zhu[17] has studied the typical point defects in Au–Ag alloy, such as He atom interstice, vacancy and its cluster, by using the density functional theory (DFT), and evaluated the formation energy for He atom in individual defect sites. These results show that the relative stability of point defects and the formation energy for He in Au–Ag alloy are closely related to the atomic configuration of host atom in the vicinity of defect site and mass density.

To our knowledge, although some research groups have employed first principles calculation within the framework of DFT to study the physical properties of Au–Ag alloy and the microscopic behaviors of He defects, few reports have paid attention to the molecular dynamics (MD) simulation[18–22] for He behavior in Au–Ag alloy. In this work, we employ MD method on basis of embedded atom method (EAM) to analyze the physical properties and He behaviors in Au and Ag metal, which can be useful for understanding He point defects in Au–Ag alloy, even δ phase Pu–Ga alloy. As mentioned earlier, experimental work poses a huge challenge due to the special character of Pu-based system, so we plan to perform an MD simulation on alternative candidate for δ phase Pu–Ga alloy (i.e., Au–Ag alloy) in a future work.

2. Computational details

Face-centered cubic (fcc) metal usually possesses a tetrahedral interstitial site comprised of four atoms, an octahedral interstitial site made up of six atoms, and a substitutional site originating from an impurity atom replacement of a host atom. To estimate the formation energy for point defects, we first construct a supercell including 1.6×104 atoms, then add or delete atoms to model the corresponding defect configuration. A simulation model for defect configuration is shown in Figs. 1(a)–1(c). All of the calculations in this work are implemented with the classical molecular dynamics package-LAMMPS code. Periodical boundary condition is employed in all cases. For the formation energy of interstitial atom, the annealing molecular dynamics method is used to completely relax a system including interstitial atom, and obtain an atomic configuration with the minimum energy.

Fig. 1. Three typical defect sites in fcc Au and Ag metal: (a) octahedral interstitial site, (b) tetrahedral interstitial site, and (c) substitutional sites, with blue and red sphere denoting host atom Au/Ag and interstitial atom, respectively.

For an initial configuration, the temperature slowly increases to 300 K during 5×105 steps in the NVT ensemble; the time step is set to be 0.5 fs. An interstitial atom is added to a defective site when temperature reaches 300 K, the system is then completely relaxed through isothermal process of 5000 steps in the NPT ensemble. Next, the system slowly cools down to 1×10−4 K during 5×104 steps in the NVT ensemble. Finally, we obtain an energetically optimal configuration including the point defects.

In the MD simulation, we use Au, Ag, and Au–Ag embedded atom model (EAM) potentials of Zhou et al.[23,24] and He–He potential of Valone et al.[25] For Au–He and Ag–He cross potentials, we perform a first principles calculation on a hypothetical Au3He/Ag3He crystal (L12 lattice structure) within space group of , and fit to a revised form of universal equation of state of Rose et al.[1,26]

where Ec, re, Ω, and B are the cohesive energy, nearest-neighbor distance, atomic volume, and bulk modulus at equilibrium reference structure, respectively; δ is a dimensionless quantity related to pressure derivative of the bulk modulus.

The first principles calculations are implemented by density functional theory through using all-electron full potential linearized augmented plane wave (FP-LAPW) method within the framework of WIEN2K code.[27–29] The exchange–correlation energy is approximated with Perdew–Burke–Ernzerhof (PBE)[30] form of generalized gradient approximation (GGA). The maximum l value for partial waves used inside the muffin-tin (MT) sphere is lmax = 10. The cutoff parameter is Rmt×Kmax = 9. In the interstitial region, the charge density and the potential are expanded into a Fourier series with wave vectors up to Gmax = 12 a.u.−1. The MT radius values are set to be 2.00 Bohr, 2.00 Bohr, and 1.60 Bohr for Au, Ag, and He atoms, respectively. Optimized lattice constants for Au3He and Ag3He are 4.0671 Å and 4.1256 Å. The modified EAM (MEAM) potential parameters for Au–He and Ag–He are shown in Table 1.

Table 1.

MEAM potential parameters for Au–He and Ag–He interatomic potential. MEAM parameters for cross potential. Parameters are for a fit to a Rose curve.

.

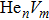
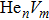
For the formation energy of cluster (V denotes vacancy), we delete a host atom in the center site of the simulation cell to model a mono-vacancy defect. We then fully relax this system to reach a new energy equilibrium state. Next, we estimate the total energy of every atom in this system, delete the atom with the maximum energy, and obtain di-vacancy defect. We then further estimate the formation energy of di-vacancy. The vacancy number gradually increases, and we obtain a vacancy cluster with a different size and structure. For cluster, we introduce a He atom in the above vacancy cluster, then the system is fully relaxed to reach a new energy equilibrium state. Next, we will obtain an atomic configuration containing cluster and with a minimum energy, and further estimate the formation energy of this cluster. Then, we add another He atom into this system. Finally, we estimate the formation energy of the corresponding system. The largest cluster includes eight vacancies and seven He atoms in this work, hence .

Self-interstitial atom (SIA) is an elementary point defect in crystal lattice, in which a host atom occupies an interstitial site. Formation energy is a criterion for structural stability of impurity doping and/or chemical reaction in metallic material. Thus the formation energy of SIA can be used to understand the structural properties of point defect. Formation energy of SIA is given by

where X denotes the host atom (Au/Ag atom in this work), i.e., Ec(Au)=3.93 eV and Ec(Ag)=2.85 eV; Ec(16000X) is the total energy of the ideal lattice including 16000 metallic atoms; Ec(16001X) is the total energy of above system including an SIA.

Similarly, the formation energy of He interstitial site is given by

where X represents the Au/Ag atom, and superscript int denotes interstitial atom.

Substitutional defect for He atom represents the point defect configuration of one He atom combining with one vacancy in lattice, and reads,

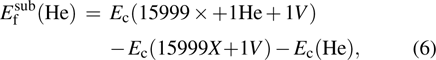where superscript sub refers to the substitutional defect, V is the vacancy, Ec(15999X+1He+1V) represents the total energy of a simulation system containing a vacancy and a He atom occupying vacancy site.

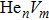
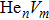
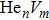
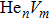
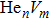
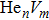
In addition, the formation energy of cluster is useful for understanding the initial stage for the nucleation of He bubble, and is given by

where Ef ( ) is the formation energy of cluster, and Etot( ) the total energy of a system containing cluster; n and m represent the number of He atoms and the number of vacancies in a cluster, respectively; N denotes the number of metallic atoms in an ideal lattice, thus (N − m) is the number of Au/Ag atoms in the simulation system.

In this work, we adopt nudged elastic band (NEB) method to calculate the migration energy for point defect diffusion at ambient temperature. In this method, several intermediate transition states between initial and final sites for atomic diffusion should be introduced. Diffusion atom can occupy a space site with a lower energy during diffusion procedure under elastic tension, automatically diffuse into these sites, and forms the so-called minimum energy path (MEP). Migration energy of atomic diffusion can be obtained by subtracting the total energy of initial site from the total energy of saddle point on the MEP[24]

where Em represents the migration energy of atomic diffusion, Es is the total energy of interstitial atom located in a saddle point on the MEP, and E0 the total energy of a system when an interstitial atom sits on the initial site. When there are more transition states for defect diffusion between the initial and final site, the saddle point will be more precise.

Migration energy for point defect diffusion at high temperature is calculated through the effective diffusion coefficient Deff, which is given by

where Dsim is the atomic diffusion coefficient, and Xd the concentration of point defects.

According to the diffusion law of Einstein, Dsim is defined as

where r(t) denotes the atomic coordinate at t, r(0) is the initial atomic coordinate, N is the dimension of simulation system and N = 3 since the system in this work are all cubic structure.

Atomic mean square displacement (MSD) is given by

From Eq. (10) with Eq. (11) one can obtain

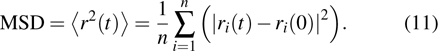By substituting Eq. (12) into Eq. (9), one can obtain the atomic effective diffusion coefficient

During simulation procedure, we introduce dozens of point defects into the simulation system, and give the effective diffusion coefficient in Eq. (13) through MSD and the concentration of point defects.

Based on classical transition state theory, Deff can be given by an approximate expression:

where l is the hopping distance between energy minima, ν the attempt frequency, Em the activation barrier, and k the Boltzmann constant. Obviously, one can obtain Em through the natural logarithm form of Eq. (14).

For the atomic effective diffusion coefficient in Au and Ag metal, we construct a simulation cell (1.6×104] atoms), and introduce vacancy, SIA and He interstitial atom of 0.5 at.%, then add a cluster composed of 16 vacancies and 80 He atoms into this system. For the estimation of atomic effective diffusion coefficient, periodical boundary condition is adopted, and initial atomic velocity obeys the Gaussian distribution. The isothermal molecular dynamics simulation is performed at six temperatures (1500 K–2000 K, in steps of 100 K) under the NPT ensemble. We then record the atomic MSD, plot MSD as a function of time, and we obtain the slope of MSD versus t curve. Finally, we deduce the atomic effective diffusion coefficient through Eq. (10) and the concentration of point defects.

3. Results and discussion
3.1. Formation energy of SIA

For the formation energy values of different defect sites in Au and Ag metal, MD simulation results are summarized in Table 2. The formation energy values of the octahedral interstitial sites are smaller than those of tetrahedral interstitial sites, indicating that the octahedral SIA is more stable than the tetrahedral SIA. This may happen because, compared with the volume for tetrahedral interstitial site, the volume for octahedral interstitial site in fcc lattice is larger and the repulsion for each atom in individual lattice site is smaller, hence an octahedral interstitial site becomes more stable.

Table 2.

Formation energy values (in unit eV) of self-interstitial atom (SIA) in Au and Ag metals. and denote formation energy for octahedral and tetrahedral interstitial sites, respectively.

.
3.2. Formation energy of He atom

In principle, the formation energy of point defect for single He atom is a fundamental characteristic for evaluating its behavior in material matrix. We mainly consider two point defect structures in Au and Ag in this work; i.e., single He atom occupying interstitial and substitution sites, respectively. The formation energy values of He atom occupying interstitial and substitutional sites in Au and Ag metals are summarized in Table 3.

Table 3.

Formation energy values (in unit eV) of He atom occupying interstitial and substitutional sites in Au and Ag metals, respectively. , , and denote formation energy for He atom occupying substitutional, octahedral interstitial and tetrahedral interstitial sites, respectively.

.

As shown in Table 3, the formation energy of the He atom occupying substitutional site in Au/Ag is a lower value than the formation energy of octahedral interstitial site, while the tetrahedral interstitial site has the largest formation energy. This implies that the defect structure with a substitutional site including one He atom and one vacancy is the most stable. As discussed later, the spatial volume close to the substitutional site is the largest value followed by the octahedral and tetrahedral interstitial sites in fcc Au/Ag lattice. As a completely filled electronic shell element, He is favorable for occupying a defect site with a larger volume, rather than bonding with other orbital electrons from its surrounding atoms, hence the stability sequence of defect sites for He atom in Au/Ag is substitutional site octahedral interstitial site tetrahedral interstitial site. This result is in good agreement with the first principles calculations of Zhu[17] and Zu et al.[31] The site occupancy and stability of defect structure for He atom are also in accord with their results, showing that the potential function and other MD parameters used in in this work are feasible.

3.3. Formation energy of He–vacancy cluster

As mentioned earlier, a He atom arising from the internal or external factors, such as α decay induced by self-irradiation and/or He implantation, prefers to combine with the surrounding vacancy defect due to its insolubility in material matrix, then produces the He–vacancy complex, i.e., He–V cluster, and finally results in the nucleation, accumulation and growth of He bubble. In principle, 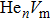cluster can be viewed as a predecessor for three-dimensional He bubble. The plots of formation energy of cluster in Au/Ag versus n for various m values and versus m for various n values are depicted in Figs. 2 and 3 ( not shown here), respectively.

Fig. 2. Plots of formation energy of 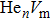cluster versus (a) number of vacancies and (b) number of He atoms in Au metal.
Fig. 3. Plots of formation energy of cluster versus (a) number of vacancies and (b) the number of He atoms in Ag metal.

As shown in Figs. 2(a) and 3(a), the formation energy of cluster gradually decreases as the number of He atoms increases, while the vacancy number is kept constant, and reaches the minimum value at n/m = 1. The formation energy of cluster then increases as the number of He atoms increases. This shows that He–V cluster is the most stable when a vacancy site is occupied by a He atom in Au/Ag metals. One can obtain a similar conclusion from Figs. 2(b) and 3(b). It is should be noted that an inflection point appears around n = m, further indicating that cluster is the most stable at n = m.

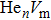
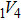
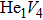
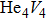
As mentioned earlier, He readily occupies a defect site with a larger volume in fcc Au/Ag since the electron density of host atom with larger spacial volume is lower, and these electrons do not bond with other orbital electrons from the surrounding atoms. Therefore, the He atom readily combines with vacancy and its cluster, and produces cluster that is the most stable at n = m. For example, for m = 4, He cluster forms when a first He atom is introduced into a V4 cluster; however, one He atom is insufficient to occupy so much space that the residue space is still large, hence cluster is unstable. When a second He atom is introduced into this cluster, the spacial volume for each He atom decreases, resulting in the decrease of degree of freedom, tending to stabilize the cluster, and further reducing formation energy, and so on. For this reason, each He atom occupies one vacancy site, and produces a stable cluster. Correspondingly, the formation energy reaches its minimum value at n = 4. If , then four vacancies are insufficient to accommodate five He atoms. The He atom will mutually repulse other He atoms, resulting in a displacement from the vacancy site and an increase of the formation energy, thus stabilizing the cluster. This finding is also in agreement with the scenarios Figs. 2 and 3, thus further implying that cluster is the most stable at n = m.

3.4. Migration energy of point defect at ambient temperature

For three typical point defects in metallic Au and Ag including vacancy, SIA, and He interstitial atom at ambient temperature, we employ the nudged elastic band method (NEB) to estimate the migration energy values for these three defects diffusing into 1NN, 2NN, and 3NN sites, respectively, and analyze the diffusion property and mechanism for each of these point defects. An interstitial atom occupying the octahedral site and an interstitial atom occupying the tetrahedral site diffusing into their corresponding neighboring sites are shown in Figs. 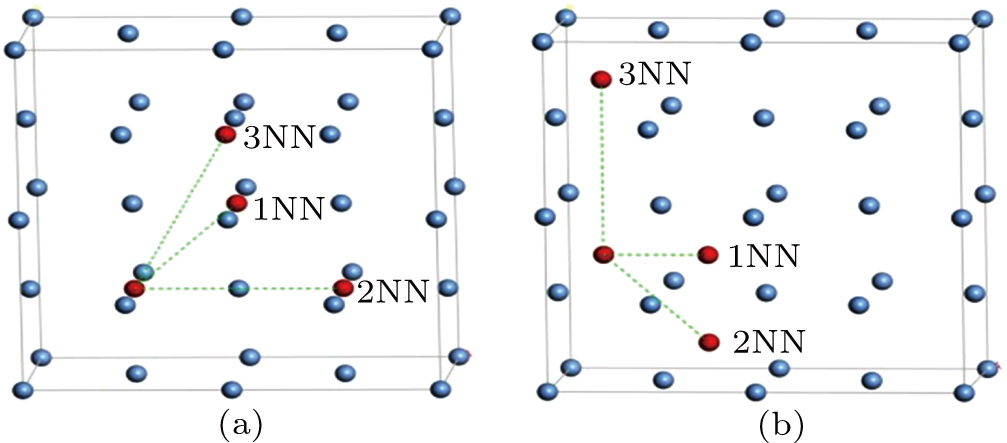4(a) and 4(b), respectively. To investigate the migration energy of point defect at ambient temperature, we consider 18 transition states in total.

Fig. 4. Schematic diagrams for interstitial atom diffusing into neighboring sites: (a) octahedral interstitial site in fcc Au and (b) tetrahedral interstitial site in fcc Au metal.

Figures 5(a) and 5(b) show the plots of total energy versus reaction coordinate for mono-vacancy diffusion in Au and Ag metal, respectively. The migration energy values deduced from Eq. (5) are summarized in Table 4.

Fig. 5. Plots of total energy versus reaction coordinate for mono-vacancy diffusing into its 1NN, 2NN, and 3NN in (a) Au and (b) Ag metal.
Table 4.

Migration energy values (in unit eV) of mono-vacancy diffusing into its 1NN, 2NN, and 3NN in Au and Ag metals. Em (iNN) (i = 1, 2, 3) refer to migration energy of mono-vacancy diffusing into its i-th nearest neighbor.

.

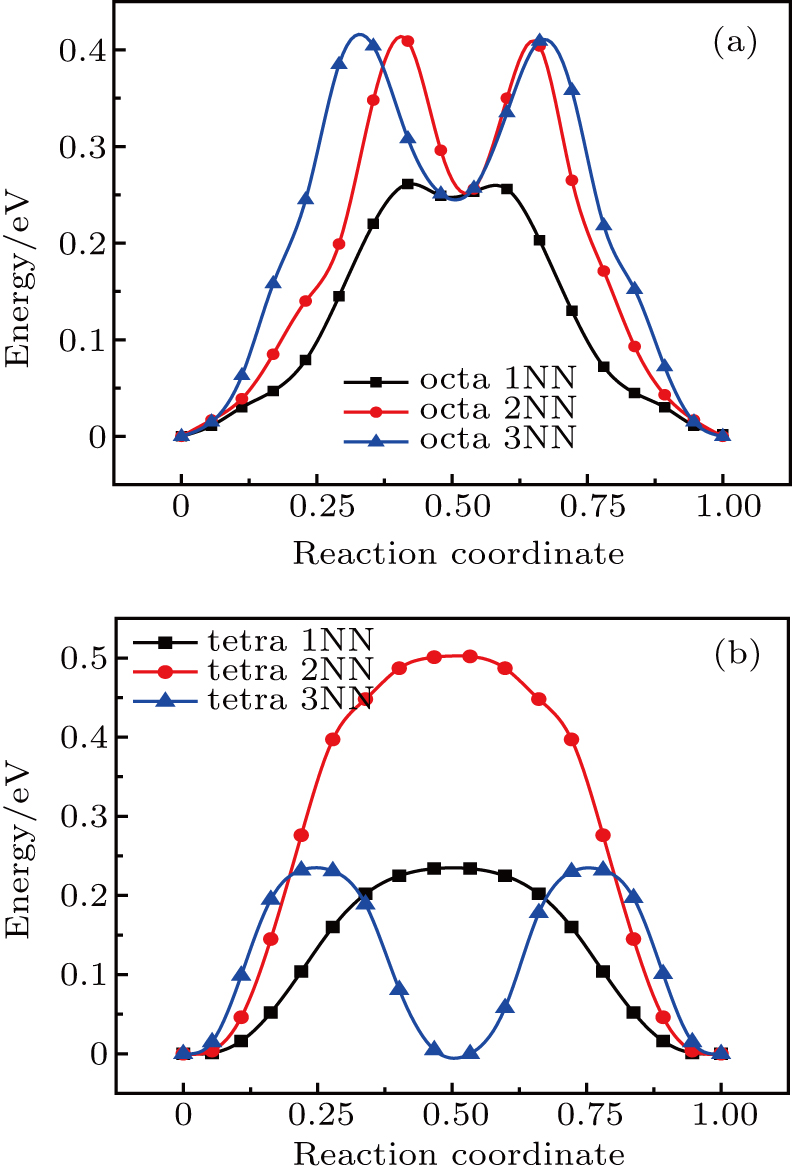
As shown in Table 4, the migration energy of mono-vacancy diffusing into 1NN site is smaller than into 2NN, and 3NN site. This indicates that the mono-vacancy is more apt to diffuse into its 1NN site, which is in agreement with experimental data of Zhu,[17] and thus further verifies the universality and feasibility of interatomic potential employed in this work.

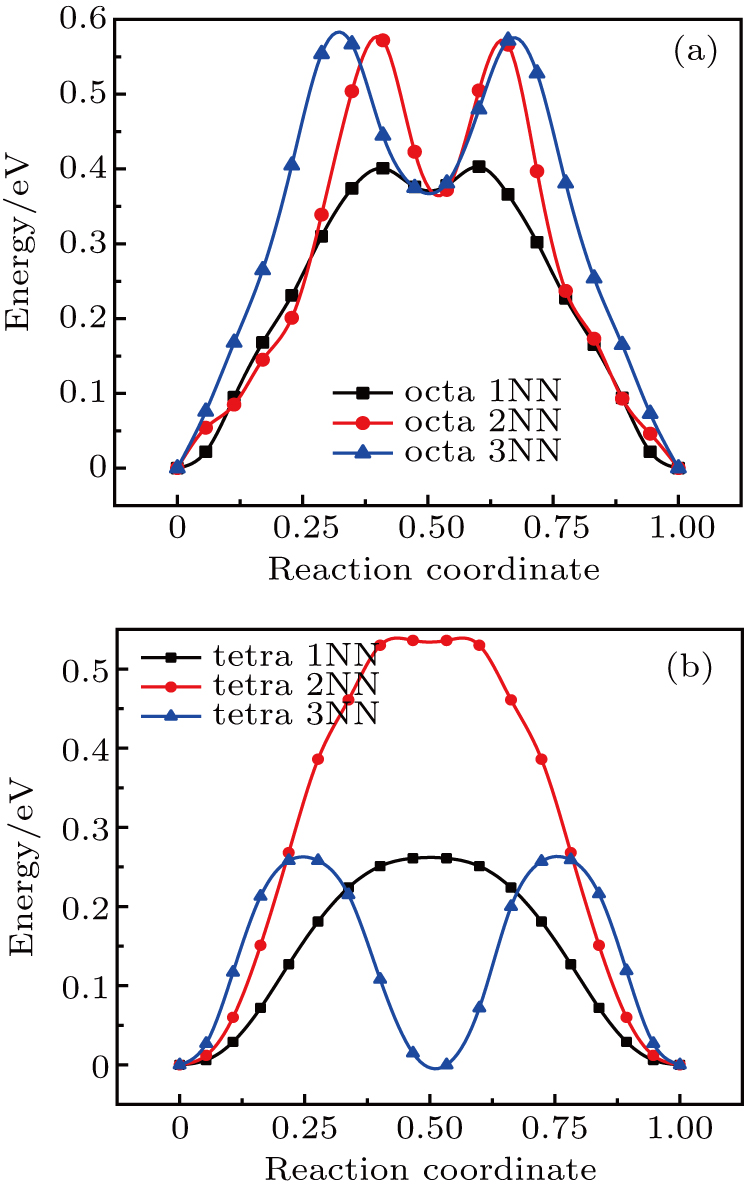For the fcc Au and Ag crystal, we consider two typical defect structures for self-interstitial atom (SIA), i.e., the octahedral and tetrahedral site, and estimate the migration energy values of SIA located in these two defect sites diffusing into its 1NN, 2NN, and 3NN sites. The plots of total energy versus reaction coordinate for SIA along its diffusion path are shown in Figs. 6 and 7. The values of migration energy Em deduced from Eq. (5) are summarized in Table 5.

Fig. 6. Plots of total energy versus reaction coordinate for (a) octahedral and (b) tetrahedral SIAs diffusing into its 1NN, 2NN, and 3NN sites in Au metal.
Fig. 7. Plots of total energy versus reaction coordinate for (a) octahedral and (b) tetrahedral SIAs diffusing into its 1NN, 2NN, and 3NN sites in Ag metal.
Table 5.

Migration energy values (in unit eV) of the octahedral and tetrahedral SIAs diffusing into its 1NN, 2NN, and 3NN in Au and Ag metals. Em (octa) and Em (tetra) are migration energy of the octahedral and tetrahedral SIAs diffusing into their corresponding neighboring sites, respectively.

.

The migration energy for SIA (Table 5) located at the octahedral or tetrahedral site diffusing into its 1NN site is the minimum value, indicating that the SIA most likely diffuses into its 1NN site in Au and Ag. As shown in Fig. 6(a) and Fig. 7(a), there are two peaks in the plot of total energy versus reaction coordinate for each of 2NN diffusion and 3NN diffusion in the octahedral defect structure, and their minimum values are close to the peak value of 1NN diffusion, implying that 2NN and 3NN diffusion for the octahedral SIA each leads to an intermediate defect structure similar to 1NN site.

Figures 6(b) and 7(b) each show that two peaks appear in the 3NN diffusion curve for the tetrahedral SIA, and its peak value is close to the peak value of 1NN diffusion curve. However, its minimum value is close to zero energy, which indicates that the 3NN diffusion for the tetrahedral SIA gives rise to an intermediate site similar to its initial structure. In fact, as shown in Fig. 4, the 3NN site can be viewed as an intermediate site between two continuous 1NN diffusion for SIA, thus the 3NN diffusion curve may be viewed as a combination of two curves for 1NN diffusion.

The plots of the total energy versus reaction coordinate for 1NN, 2NN, and 3NN diffusion for He interstitial atom in Au and Ag metal, estimated with NEB method, are shown in Figs. 8 and 9, and the values of migration energy Em deduced from Eq. (5) are summarized in Table 6. The diffusion of SIA, He interstitial atom prefers to diffuse into its 1NN site, no matter whether it is the octahedral or tetrahedral interstitial site (see Table 6).

Fig. 8. Plots of total energy reaction coordinate for (a) octahedral and (b) tetrahedral He interstitial atom diffusing into their corresponding neighboring sites in Au metal.
Fig. 9. Plots of total energy versus reaction coordinate for (a) octahedral and (b) tetrahedral He interstitial atom diffusing into their corresponding neighboring sites in Ag metal.
Table 6.

Migration energy values (in unit eV) of 1NN, 2NN, and 3NN diffusion for He interstitial atom in Au and Ag metals. Em (octa) and Em (tetra) are migration energy value of octahedral and tetrahedral He interstitial atoms diffusing into their corresponding neighboring sites, respectively.

.

As shown in Figs. 6–9, He interstitial atom and SIA in Au metal have diffusion characteristics similar to those in Ag metal, e.g., for the diffusion of the octahedral interstitial site, the 2NN and 3NN diffusions of He interstitial atom also lead to a 1NN-like site, resulting in two peaks in the energy curve of 2NN and 3NN diffusions, and their minimum values are close to the peak value of 1NN diffusion. Similarly, the 3NN diffusion of He interstitial atom gives rise to a site similar to its initial structure, and also results in two peaks for the 3NN diffusion, of which peak value is close to that of 1NN diffusion.

3.5. Migration energy of point defect at high temperature

To further understand the diffusion of SIA and vacancies in Au and Ag metal, we also estimate the atomic effective diffusion coefficient for a simulation system containing 80 vacancies and SIAs, respectively. The isothermal molecular dynamics simulation is implemented in a total time of 5 ns at each fixed temperature under the NVT ensemble, and the plots of MSD for these six temperatures are plotted in Figs. 10 and 11. Finally, we obtain the slopes of MSD–t curve through linearly fitting Dsim and Deff in Eqs. (12) and (13) as summarized in Table 7.

Fig. 10. Plots of simulated MSD versus time for (a) vacancies and (b) SIA defects in Au metal at temperatures T = 1500 K, 1600 K, 1700 K, 1800 K, 1900 K, and 2000 K, respectively.
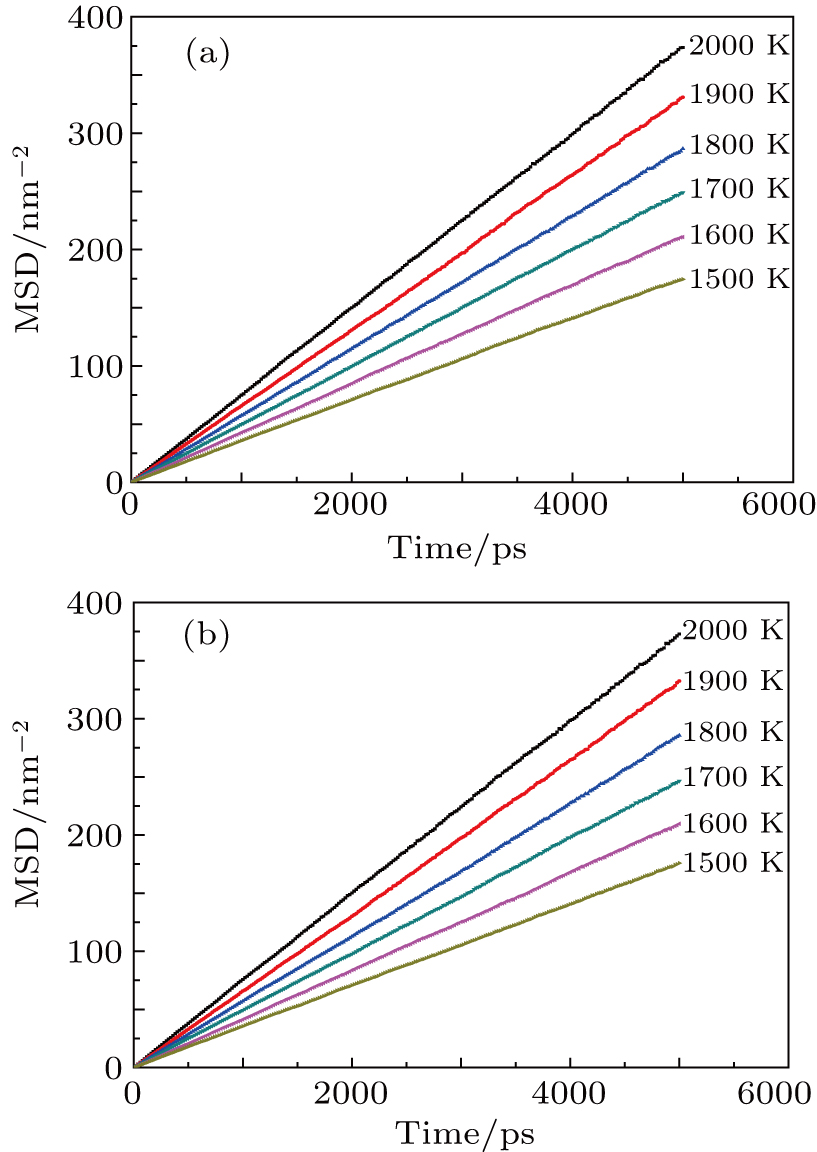Fig. 11. Plots of simulated MSD versus time for (a) vacancies and (b) SIA defects in Ag metal at temperatures T = 1500 K, 1600 K, 1700 K, 1800 K, 1900 K, and 2000 K, respectively.
Table 7.

Atomic effective diffusion coefficients for vacancies and SIAs in Au and Ag metals. V denotes vacancy, and Dsim and Deff are deduced from Eqs. (9) and (10), respectively.

.

As indicated in Table 7, the atomic diffusion coefficient increases with temperature increasing in each of Au and Ag metal. A possible reason is that the higher the temperature, the higher the internal energy of Au/Ag lattice will be, and the more intensive the atomic thermal motion and the larger the atomic MSD will be, hence we obtain a larger atomic effective diffusion coefficient.

In the Au metal, the effective diffusion coefficient for vacancy is close to that for SIA at each of individual temperatures though the latter is somewhat larger than that of the former, indicating that adding SIAs into Au will give rise to a local field around the doping site, strengthen the interaction between SIA and its neighboring atoms, and increase the diffusion of the surrounding Au atoms. For Ag metal, the effective diffusion coefficient for SIA is also similar to that for vacancy at the same temperature. However, it should be noted that the surrounding Ag atom tend to diffuse into a vacancy site by introducing the vacancy defect, which will increase the total effective diffusion coefficient. This result implies that the vacancy defect can activate the host atoms and thus enhance the diffusion behavior.

To understand the influence of He atom and He–vacancy cluster on the diffusion characteristic in metallic matrix, we estimate the effective diffusion coefficients for these defects in Au and Ag metals. For this purpose, we first introduce 80 He atoms and a cluster into each of Au and Ag crystal, and carry out an isothermal molecular dynamics simulation with a total simulation time of 5.0 ns under the NVT ensemble. The atomic MSD as a function of simulation time t at T = 1500 K, 1600 K, 1700 K, 1800 K, 1900 K, and 2000 K are plotted in Figs. 12 and 13. Next, we obtain the slopes of MSD versus t curve through linear fitting of Dsim and Deff in Eqs. (12) and (13), and summarized in Table 8.

Fig. 12. Plots for simulated MSD versus time for (a) He atom and (b) He–vacancy defects in Au metal at temperatures T = 1500 K, 1600 K, 1700 K, 1800 K, 1900 K, and 2000 K, respectively.
Fig. 13. Plots of simulated MSD versus time for (a) He atom and (b) He–vacancy defects in Ag metal at temperatures T = 1500 K, 1600 K, 1700 K, 1800 K, 1900 K, and 2000 K, respectively.
Table 8.

Atomic effective diffusion coefficients for He atom and He–vacancy cluster defects in Au and Ag metals. He and He–V denote He atom and He–vacancy cluster, respectively. Dsim and Deff are deduced from Eqs. (12) and (13), respectively.

.

In analogy to diffusion of vacancy and SIA, for He atom and He–vacancy cluster in Au and Ag metals, as shown in Table 8, the atomic effective diffusion coefficient would increase with temperature increasing. A possible reason is that the higher the temperature, the higher the internal energy of Au/Ag lattice will be, and the more intensive the atomic thermal motion, the larger the atomic MSD will be, hence we obtain a larger atomic effective diffusion coefficient. In Au and Ag metals, the effective diffusion coefficient for He atom is close to that for He–vacancy cluster at each of individual fixed temperatures, although the latter is somewhat smaller than the former, indicating that the further introducing of vacancy defects into Au/Ag crystal will result in the reduction of the interaction between vacancy and its neighboring atoms, and decrease of diffusion velocity for the surrounding Au/Ag atoms. For the Au metal as shown in Tables 7 and 8, the atomic diffusion coefficients for He atom and He–V cluster are remarkably smaller than those of vacancy and SIA, showing that He atom and He–V cluster obviously suppress diffusion of Au atoms, which is contrary to what the vacancy and SIA do. It is interesting to note that the diffusion coefficients for these four point defects are close to each other.

The migration energy values at high temperature, derived from the effective diffusion coefficient, are listed in Table 9. The migration energy is much smaller than the value at ambient temperature, which is consistent with the physical intuition.

Table 9.

Migration energy values (in unit eV) of eight systems at high temperature.

.
4. Summary remark and outlook

In this work, we estimate the formation energy and effective diffusion coefficient of point defects in Au and Ag metals by using MD method, and employ the NEB method to estimate the migration energy of point defect diffusion. The results show that the octahedral SIA is more stable than tetrahedral SIA. Stability sequence of point defects for He atom is substitutional site octahedral interstitial site tetrahedral interstitial site. cluster reaches the highest stability when the number of He atoms equals that of vacancies; i.e., n = m. For mono-vacancy diffusion, energetically, 1NN site can be the most favourable site. In analogy to SIA, the 2NN and 3NN diffusion for the octahedral SIA will give rise to an intermediate defect structure similar to 1NN site. Note, however, that the 3NN diffusion for each of tetrahedral SIA and He atom will lead to an intermediate site in analogy to its initial structure. For the effective diffusion of point defects, the introduction of vacancy, SIA, He atom and He–V cluster may have a similar effect on diffusion velocity in Ag metal. This work could be viewed as a preliminary work for investigating He behaviour in Au–Ag alloy, even the nucleation and growth mechanism for He bubble in aging Pu–Ga alloy. In future work, we plan to employ the MD method and/or mesoscopic technique to simulate the properties of point defects, such as SIA, He–V cluster and He bubble in Au–Ag/Pu–Ga alloys, and compare theoretical result with available experimental data, such as from TEM, SEM, and PAS examinations of He-implanted and/or aging sample.

Reference
[1] Baskes M L 2000 Phys. Rev. B 62 15532 https://doi.org/10.1103/PhysRevB.62.15532
[2] Pochet P 2003 Nucl. Instrum. Method B 202 82 https://doi.org/10.1016/S0168-583X(02)01835-9
[3] Ao B Y Wang X L Hu W Y Yang J Y Xia J X 2007 J. Alloys Compd. 444–445 300 https://doi.org/10.1016/j.jallcom.2006.11.077
[4] Ao B Y Chen P H Shi P Wang X L 2012 Commun. Comput. Phys. 11 1205 https://doi.org/10.4208/cicp.290610.210111s
[5] Robinson M Kenny S D Smith R Storr M T 2012 J. Nucl. Mater. 423 16 https://doi.org/10.1016/j.jnucmat.2011.11.046
[6] Scott C Kenny S D Storr M T Willetts A 2013 J. Nucl. Mater. 442 83 https://doi.org/10.1016/j.jnucmat.2013.08.035
[7] Robinson M Kenny S D Smith R Storr M T 2014 J. Nucl. Mater. 444 493 https://doi.org/10.1016/j.jnucmat.2013.10.017
[8] Wu F C Wang P Liu X Y Wu H A 2017 J. Nucl. Mater. 484 7 https://doi.org/10.1016/j.jnucmat.2016.11.018
[9] Karavaev A V Dremov V V Ionov G V 2017 J. Nucl. Mater. 496 85 https://doi.org/10.1016/j.jnucmat.2017.09.005
10 Valone S M Baskes M L Stan M Mitchell T E Lawson A C Sickafus K E 2004 J. Nucl. Mater. 324 41 https://doi.org/10.1016/j.jnucmat.2003.09.006
11 Savrasov S Y Kotliar G Abrahams E 2001 Nature 410 793 https://doi.org/10.1038/35071035
12 Dai X Savrasov S Y Kotliar G Migliori A Ledbetter H Abrahams E 2003 Science 300 953 https://doi.org/10.1126/science.1083428
13 Moore K T Söderlind P Schwartz A J Laughlin D E 2006 Phys. Rev. Lett. 96 206402 https://doi.org/10.1103/PhysRevLett.96.206402
14 Petit L Svane A Szotek Z Temmerman W M 2003 Science 301 498 https://doi.org/10.1126/science.1086505
15 Stevens M F Zocco T Albers R Becker J D Walter K Cort B Paisley D Nastasi M 1998 Fundamental and applied studies of helium ingrowth and aging in plutonium, USA https://doi.org/10.2172/296814
16 Thomé T Grynszpan R I 2006 Radiat. Eff. Defect. S. 161 347 https://doi.org/10.1080/10420150600764181
17 Zhu Z Q Zhang Y L Xie J J Yang L Nie J L Zu X T 2016 Acta Phys. Pol. A 29 1151 https://doi.org/10.12693/APhysPolA.129.1151
18 Zhou B Zhang W Gong W B Wang S Ren C L Wang C B Zhu Z T Y Huai P 2013 Chin. Phys. Lett. 30 113402 https://doi.org/10.1088/0256-307X/30/11/113402
19 Wu T Y Peng M M Luo X F Lai W S 2013 Chin. Phys. Lett. 30 096106 https://doi.org/10.1088/0256-307X/30/9/096106
20 Zhou N G Hong T Zhou L 2012 Acta Phys. Sin. 61 028101 (in Chinese) https://doi.org/10.7498/aps.61.028101
21 Li C Niu M X Liu P Li Y F Wang D Y 2017 Chin. Phys. B 26 103401 https://doi.org/10.1088/1674-1056/26/10/103401
22 Li P Liu M H He C H Guo H X Zhang M T 2017 Chin. Phys. B 26 088503 https://doi.org/10.1088/1674-1056/26/8/088503
23 Zhou X W Wadley H N G Johnson R A Larson D J Tabat N Cerezo A Petford A K Smith G D W Clifton P H Martens R L Kelly T F 2001 Acta Mater. 49 4005 https://doi.org/10.1016/S1359-6454(01)00287-7
24 Zhou X W Wadley H N G Filho J S Neurock M N 2004 Phys. Rev. B 69 035402 https://doi.org/10.1103/PhysRevB.69.035402
25 Valone S M Baskes M I Martin R L 2006 Phys. Rev. B 73 214209 https://doi.org/10.1103/PhysRevB.73.214209
26 Rose J H Smith J R Guinea F Ferrante J 1984 Phys. Rev. B 29 2963 https://doi.org/10.1103/PhysRevB.29.2963
27 Schwarz K Blaha P Madsen G K H 2002 Commun. Comput. Phys. 147 71 https://doi.org/10.1016/S0010-4655(02)00206-0
28 Schwarz K 2003 J. Solid State Chem. 176 319 https://doi.org/10.1016/S0022-4596(03)00213-5
29 Schwarz K Blaha P Trickey S B 2010 Mol. Phys. 108 3147 https://doi.org/10.1080/00268976.2010.506451
30 Perdew J P Burke K Ernzerhof M 1996 Phys. Rev. Lett. 77 3865 https://doi.org/10.1103/PhysRevLett.77.3865
31 Zu X T Yang L Gao F Peng S M Heinisch H L Long X G Kurtz R J 2009 Phys. Rev. B 80 054104 https://doi.org/10.1103/PhysRevB.80.054104