† Corresponding author. E-mail:
Controlling the phase of light in magnetoplasmonic structures is receiving increasing attention because of its already shown capability in ultrasensitive and label-free molecular-level detection. Magneto–optical Kerr reversal has been achieved and well explained in nanodisks by using the phase of localized plasmons. In this paper, we report that the Kerr reversal can also be produced by surface plasmon polaritons independently. We experimentally confirm this in Co and Ag/Co/Ag metal nanogratings, and can give a qualitative explanation that it is the charge accumulation at the interface between the grating surface and air that acts as the electromagnetic restoring force to contribute necessary additional phase for Kerr reversal. Our finding can enrich the means of designing and fabricating magneto–optical-based biochemical sensors.
With the rise of metamaterials, magnetoplasmonics have experienced considerable development, and shows great potential applications in various fields such as all-optical magnetic data storage,[1,2] optical isolators and modulators,[3,4] and ultraprecise distance probe.[5] Gradually, one is not satisfied with limiting their visions on concentrating the electromagnetic energy of light at the interfaces to enhance magneto–optical (MO) effect.[6–11] More research has began to turn to the investigation of the sign of MO signal and the change of sign.[12–14] Especially, after Maccaferri et al. reported their magnetoplasmonic biochemical sensor showing a raw surface sensitivity of two orders of magnitude higher than that of the traditional nanoplasmonic sensor,[15] The MO Kerr rotation reversal has become a new focus thanks to its potential application in ultra-high precision environmental detection.[16,17] MO Kerr rotation reversal was found successively in isolated magnetic nanodisks,[15,18,19] and in two-dimensional magnetic metal lattice.[20] It has been known that magneto–optical Kerr rotation is due to the transverse magnetic (TM) and transverse electric (TE) mode conversion in the material, caused by spin–orbit (SO) coupling. The mode conversion between the amplitude and phase lag determines the magnitude and sign of Kerr rotation. The Kerr rotation reversal can be achieved when the phase lag between TE and TM components of the reflected light is an odd integer multiple of π / 2.[19] Previous studies usually used the additional phase of the excitation of the localized plasmons to meet the above phase condition in randomly distributed nanodisks.[19] Further, the phase of localized plasmons can be modified by surface plasmon polariton (SPP) via forming Fano resonance in ordered nanostructures to achieve the adjustable Kerr rotation reversal.[20,21]
In this paper, we show that MO Kerr rotation reversal can also be observed in the wavelength positon with only SPP mode existing. We confirm the experimental results in Co gratings and three-layer metal grating Ag/Co/Ag nanogratings and demonstrate that it is the SPP mode existing independently, providing the necessary phase condition for MO Kerr rotation reversal.
The nanograting samples were fabricated as follows. First, a 100-nm-thick photoresist (Allresist, AR P-3170) was spin-coated on a silicon substrate and followed by a pre-bake at 95 °C for 1 min. Then the photoresist film was patterned by a home-made Lloyd’s–Mirror interference lithography system. Afterwards, the exposed photoresist film was immersed in a developing solution (Allresist, AR 300–26 diluted 1:5 with deionized water) for 45 s. A grating pattern with an appropriate slit width can be produced by properly adjusting the exposure dose. We can achieve the grating patterns with different periods via changing the incident angle of the laser on the photoresist film during the exposure stage. The period of the fringe pattern can be given by λ / (2sin θ), where λ is the laser wavelength and θ is the half angle of intersection of the laser beams. In the next step, a 50-nm-thick cobalt film was deposited on the photoresist grating in turn by DC magnetron sputtering with an Ar pressure of 0.5 Pa. By changing the incident angle, we obtained two Co nanograting samples with different periods, named Co385 (with the period L = 385 nm, the width of the strip d = 210 nm) and Co325 (with L = 385 nm, d = 180 nm). We then replaced the cobalt film with a three-layer composite film of Ag/Co/Ag in the DC magnetron sputtering stage, and obtained another two grating samples, referred to as ACA385 (with L = 385 nm, d = 210 nm) and ACA325 (with L = 325 nm, d = 180 nm), respectively. All the geometric parameters of the Ag/Co/Ag nanograting samples are described in Fig.
The optical reflectivity of the three-layer nanograting sample is given priority because it is closely related to the surface plasmon (SP) mode on the grating surface. The reflectivity was measured by spectroscopic ellipsometer (J. A. Woollam M-2000) with a white light source focused into a spot with a diameter of approximately 0.5 mm. The reflectivity spectra were obtained by the ratio of the zero-order reflective signal of the samples to a base line of the light source. For one-dimensional gratings, there is no spatial confinement in the direction perpendicular to the lattice vector of the grating. So when grating samples are impinged by the incident light in the configuration shown in Fig.
In the MO measurement, an external magnetic field up to 1.6 kOe (1 Oe = 79.575 A 
In a previous study, Maccaferri et al. proposed a model of two orthogonal damped harmonic oscillators to explain the polar Kerr rotation reversal in a nanosized Ni disk.[19] The displacement of the conduction electrons on the nanodisk leads to an electromagnetic restoring force, which gives rise to an LSP mode and additional phase lag of π/2 between TE and TM components of the reflected light at the LSP excitation position. This can be extended to the qualitative explanation of why the SPP mode can give rise to the Kerr reversal. The p-polarized light with an oblique incidence has an additional z-axis electric component perpendicular to the grating/air interface besides the in-plane component along x direction, which is shown in Fig.
 |

 |
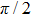
 | Fig. 4. Process of incident p-polarized light being reflected on nanograting surface and the damped harmonic oscillator model in z direction. |
In the case of longitudinal Kerr configuration, the permittivity tensor of an MO active material can be described as an antisymmetric matrix with 

 |
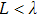
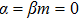
In this work, using interference lithography and DC magnetron sputtering, we have fabricated Co and Ag/Co/Ag nanogratings of different periods. We use different means to exclude the possible influence of LSP mode in the gratings of the two materials, and experimentally confirm that the SPP mode in our grating samples can gives rise to the reversal of MO Kerr rotation. We also give it a qualitative explanation that it is the charge accumulation at the interface between the grating surface and air that acts as the electromagnetic restoring force to contribute additional phase when the SPP mode is excited. Producing Kerr reversal via the excitation of SPP mode gives us a new approach to designing and fabricating the MO-based biochemical sensors, which have shown ultrahigh sensitivity to the surrounding refractive index and unlimited value of figure-of-merit. Furthermore, it can be predicted that when compared with the LSP mode caused Kerr reversal, the SPP mode-induced Kerr reversal should have good tunability due to the more flexible excitation wavelength and better compatibility with waveguide mode.[23] We hope that our work will conduce to the development of the highly sensitive MO-based bio/chemosensing sensors.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 |




